Comments 209
У меня из подобного, по школьной физике до сих пор непосчитанная задачка про «составить формулу в общем виде — сколько нужно затратить работы, чтобы повернуть на 180 градусов вокруг своего центра массы пирамиду, которая погружена своей вершиной в воду до центра масс). Так и храню черновик с чертежами, надо будет скормить какой-нить математике или матлабу :)
Водоизмещение пирамиды не зависит от угла её наклона. Соответственно, центр тяжести не должен сместься.
Взаимоисключающие параметры. Попробуйте это нарисовать — сами увидите, что либо постоянный объём подводной части, либо постоянная высота центра масс.
Из рисунка выше видно, что слева и справа площади закрашенных фигур равны, а значит и незакрашенные площади слева и справа тоже равны.
Почему-то мне не никак видно равенство площадей.
Один из вариантов: надо обозначить сторону большого квадрата как a+b, с одной стороны представить его площадь как сумму квадрата гипотенузы и четырёх площадей треугольника, а с другой стороны как квадрат его стороны
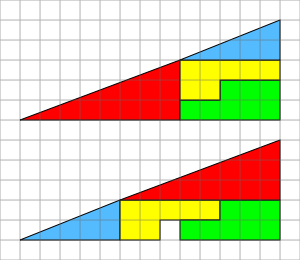
Так вот за счёт небольших перекрываний вдоль стыков на нижнем рисунке площадь одной клеточки экономится.
Просто нужно пояснить, что БОЛЬШОй треугольник (8х13) — вовсе не треугольник, а четырёхугольник! И во втором случае он более выпуклый, чем в первом.
Визуально это становится понятным, если наложить на треугольник 8х3 сверху треугольник 5х2 — у треугольника 8х3 угол более острый.
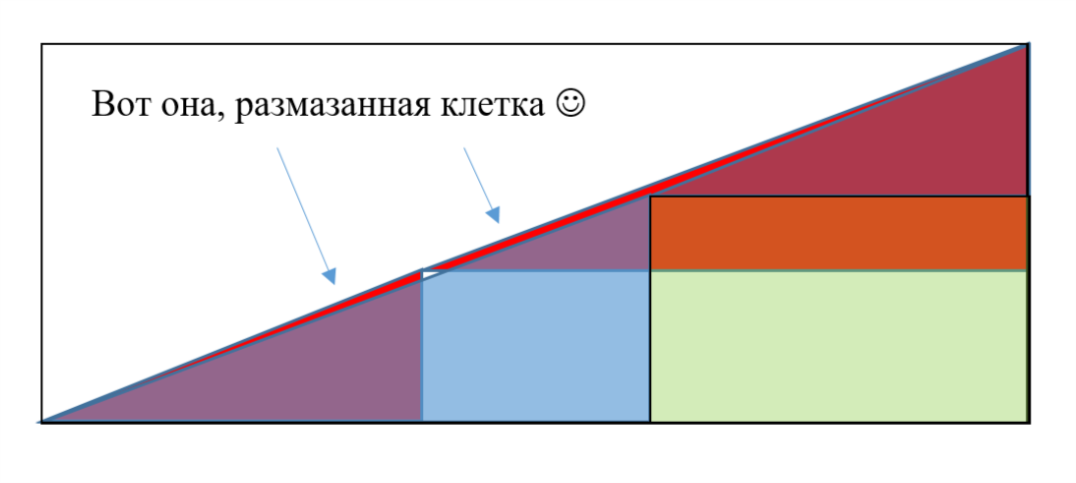
До сих пор не могу понят, в чем тут подвох. Не подскажете?
Красный и синий треугольники не подобны, а следовательно гипотенуза большого треугольника на самом деле не гипотенуза, и вообще не прямая.
В 1783 году теорема была представлена Парижской академии наук.
ru.wikipedia.org/wiki/Теорема_де_Гуа
Интересно, американцы в курсе, что теорема была за два века до них или считают себя младшими братьями Пифагора?))
В новосибе нет математических школ/кружков?
Только потом вспомнил, что таких пар нет.
Правда, тройки наверняка есть. Или хотя бы четвёрки. Уж не кроется ли геометрический смысл теоремы Ферма в геометрии высших измерений?
На самом деле маловероятно, что вся та орава ферматистов об этом не подумала, но а вдруг? Да и потом, просто интересно порассуждать на эту тему. А геометрические решения обычно самые наглядные (если не выше 3д) — например, экстремум глазами найти проще на графике (с нужным масштабом и всем остальным), чем аналитически.
a^2 + b^2 = c^2 — решения существуют. Каждому решению соответствует треугольник с некими характеристиками.
a^3 + b^3 = c^3 — не существует. Что если каждому решению соответствует некая геометрическая фигура, невозможная в евклидовом 2д? И из-за её невозможности и решений нет. Причём, вероятно, она тоже должна быть прямоугольной, как и треугольник.
А попробуем так:
a^3 + b^3 + с^3 = d^3 — решения есть, и каждому соответствует пирамидка в 3д. С некими характеристиками.
a^4 + b^4 + c^4 = d^4 — есть ли решения? А у a^n + b^n + c^n = d^n для n >= 5? Связаны ли с ними какие-нибудь фигуры? Что если там тоже появляются невозможные фигуры, и обобщение теоремы Ферма на большее количество слагаемых?
Вот как-то вот так.
Теорема Ферма, что для любого натурального числа n>2 уравнение:
a^n+b^n=c^n
не имеет решений в целых ненулевых числах a,b,c.
судя по всему у этой теоремы д.б. расширение типа
x(1)^n+x(2)^n+...x(m)^n = X^n
где m — метрика пространства
с тем же самым ограничением для n>2
видимо это д.б. как-то связано с каким-то из фундаментальных свойств m-мерного пространства.
связь безусловно есть. по-крайней мере теорема ферма утверждает, что в двумерном пространстве нет возможности создать еще одну теорему Пифагора с каким-то иным доказательством и свойствами.
возможно это свойство пифагоричности пространства?
: о)
Некая связь есть.
Теорема утверждает, что для любого натурального числа n>2 уравнение:
a^n + b^n = c^nне имеет решений в целых ненулевых числах a,b,c.
Что можно перефразировать так: Теорема Пифагора работает только для фигур в двухмерном пространстве. В трехмерном (и больше) пространстве куб (четвёртая степень и т.п) двух "граней" не даст куб (четвёртую степень и т.п.) "основания".
В целом доказательство от Техасского университета про то, как связать квадраты граней и квадрат основания почти что является доказательством Великой Теоремы Ферма от противного. Потому что для большего количества измерений нужно увеличивать количество граней, а не степень для каждой грани.
этот момент был самым ярким и самым запоминающимся. Я испытал полную гамму чувств, эмоций, переживаний первооткрывателя
Вот это классное ощущение и есть доказательство того, что наука и самообразование могут приносить физическое удовольствие. Помню подобный эпизод из школы. Когда нам учительница предложила пари: мы решаем задачу «из университета» и она нам ставит пятерку за верный ответ. Причем пятерка была, с ее слов, приравнена к оценке за контрольную.
Класс на эти пару дней преобразился, мало кто бегал на перемене, почти все думали над задачей. Даже те, кто не очень любил геометрию или был «двоечником».
Ко мне решение пришло утром, почти во сне, записал его и бегом побежал в школу. М — мотивация. Занятно, что решений было несколько, на уроке мы их разобрали и это был хороший опыт. Жаль единичный.
Но у вас неправильная формулировка.
- На рисунке пирамида трехгранная.
(Египетские пирамиды четырехгранные) - Не один из углов должен быть прямой, а именно верхний — для пирамиды "на боку" как на рисунке, теорема не выполняется.
Возьму на себя смелость альтернативной формулировки: "у трехгранной пирамиды, у которой в одной из вершин грани сходятся под прямым углом, сумма квадратов площадей этих граней равна квадрату площади оставшейся грани"
Теорема Пифагора, конечно, легко доказывается, но то, что в a, b, c можно подставить натуральные числа теорема же не доказывает. Для меня до сих пор остается загадкой почему существуют такие тройки и почему их так много (начиная с самых малых). Если бы такие тройки существовали из каких-то огромных чисел типа 7978^2 + 24791874^2 = 7226746^2, то это было бы не удивительно, поскольку можно было бы сослаться на совпадение. Даже не было бы удивительным, если бы не существовало бы ни одного набора натуральных чисел, для которых a^2 + b^2 = c^2
Может кто-нибудь знает теорему по этому вопросу?
Примитивные пифагоровы тройки
Давайте увеличим в n раз — а вот и троечка (3n, 4n, 5n). Таким образом, таких треугольников как минимум столько же, сколько и действительных чисел.
Скорее натуральных, мощность NxNxN такая же, что и N, а пифагоровы тройки являются подмножеством этого множества :)
С квадратами также. Допустим, Вы собираете a² + b² + c² = d² и хотите собрать 81 из ровно 3 чисел. Но чисел на выбор у Вас достаточно много: это и 1, и 4, и 9, и 16, и 25, и 36, и 49, и 64. Суммарно 8 чисел. Из них можно собрать:
14, 21, 26, 29, 30, 35, 38, 41, 42, 45, 46, 49, 50, 53, 54, 56, 59, 61, 62, 65, 66, 69, 70, 74, 75, 77, 78, 81, 83, 84, 86, 89, 90, 93, 94, 98, 101, 104, 105, 109, 110, 114, 116, 117, 122, 125, 129, 138, 149 — суммарно 49 чисел. Т. е. из 150 чисел мы можем собрать треть, поэтому такие «совпадения» неудивительны. Если выйти за пределы восьмёрки, то из 150 чисел соберётся 70 — это почти половина.
Из комбинаций двух квадратов тоже можно собрать много чисел:
5, 10, 13, 17, 20, 25, 26, 29, 34, 37, 40, 41, 45, 50, 52, 53, 58, 61, 65, 68, 73, 74, 80, 82, 85, 89, 90, 97, 100, 101, 104, 106, 109, 113, 116, 117, 122, 125, 130, 136, 137, 145, 146, 148, 149, 153, 157, 160, 164, 169, 170, 173, 178, 180, 181, 185, 193, 194, 197, 200 и т. д.
Если собирать a² + b², то:
Из 1000 первых чисел собираются 293 числа (29%). Среди них собираются 11 квадратов из 31 (35%).
Из 10000 чисел — 2649 (26%). 52 квадрата из 100 (52%).
Из 100 тыс чисел — 23760 (24%). 220 квадратов из 316 (70%).
Из 1 млн чисел — 215594 (22%). 881 квадрат из 1000 (88%).
Если собирать a² + b² + c², то:
Из 1000 первых чисел собираются 728 чисел (73%). Среди них собираются 19 квадратов из 31 (61%).
Из 10000 чисел — 8166 (82%). 82 квадрата из 100 (82%).
Из 100 тыс чисел — 83102 (83%). 294 квадрата из 316 (93%).
Из 1 млн чисел — 833039 (83%). 973 квадрата из 1000 (97%).
[…]
С квадратами также. Допустим, Вы собираете a² + b² + c² = d² и хотите собрать 81 ровно из 3 чисел. Но чисел на выбор у Вас достаточно много: это и 1, и 4, и 9, и 16, и 25, и 36, и 49, и 64. Суммарно 8 чисел. Из них можно собрать:
3, 6, 9, 11, 12, 14, 17, 18, 19, 21, 22, 24, 26, 27, 29, 30, 33, 34, 35, 36, 38, 41, 42, 43, 44, 45, 46, 48, 49, 50, 51, 53, 54, 56, 57, 59, 61, 62, 65, 66, 67, 68, 69, 70, 72, 73, 74, 75, 76, 77, 78, 81, 82, 83, 84, 86, 88, 89, 90, 93, 94, 96, 97, 98, 99, 101, 102, 104, 105, 107, 108, 109, 110, 114, 116, 117, 121, 122, 123, 125, 129, 132, 134, 136, 137, 138, 144, 147, 149 — суммарно 89 чисел. Т. е. из 150 чисел мы можем собрать больше половины, поэтому такие «совпадения» неудивительны. Если выйти за пределы восьмёрки, то из 150 чисел соберётся 105 — это 70%.
Из комбинаций двух квадратов тоже можно собрать много чисел:
2, 5, 8, 10, 13, 17, 18, 20, 25, 26, 29, 32, 34, 37, 40, 41, 45, 50, 52, 53, 58, 61, 65, 68, 72, 73, 74, 80, 82, 85, 89, 90, 97, 98, 100, 101, 104, 106, 109, 113, 116, 117, 122, 125, 128, 130, 136, 137, 145, 146, 148, 149, 153, 157, 160, 162, 164, 169, 170, 173, 178, 180, 181, 185, 193, 194, 197, 200 и т. д.
Если собирать a² + b², то:
Из 1000 первых чисел собираются 309 чисел (31%). Среди них собираются 10 квадратов из 31 (32%).
Из 10000 чисел — 2691 (27%). 42 квадрата из 100 (42%).
Из 100 тыс чисел — 23874 (24%). 162 квадрата из 316 (51%).
Из 1 млн чисел — 215908 (22%). 567 квадратов из 1000 (57%).
Если собирать a² + b² + c², то:
Из 1000 первых чисел собираются 800 чисел (80%). Среди них собираются 23 квадрата из 31 (74%).
Из 10000 чисел — 8283 (83%). 88 квадратов из 100 (88%).
Из 100 тыс чисел — 83268 (83%). 301 квадрат из 316 (95%).
Из 1 млн чисел — 833251 (83%). 982 квадрата из 1000 (98%).
А чего тройки то? Четверки же: https://ru.wikipedia.org/wiki/Пифагорова_четвёрка
Про целочисленный прямоугольный параллелепипед есть нерешенная проблема: https://ru.wikipedia.org/wiki/Совершенный_кубоид
Примерно похожее чувство я испытал в школе, в классе 7-ом, когда, как мне тогда казалось, я открыл "свойство" (или формулу) нахождения диагонали у куба. Просто одну сторону умножить на корень из 3. И совсем скоро я расстроился, многие об этом давно знали.
Спасибо, автор, разделяю Ваши чувства и ощущения ;-)
Я тоже что-то открывал, но уже не помню, что. Потом оказалось, что это очень простое следствие из свойств умножения и сложения.
Вы ещё молоды, можно понять. Я в университете в дипломной работе придумал по сути новый способ доказательства для определенного класса задач. Так и написал в дипломной — новый способ… Научный (к слову гениальный учёный), который и предложил идею, посоветовал быть поскромнее. Фразу эту убрал .) У нас не особо принято хвастаться в науч. сфере, я так понял что хорошим тоном считается, когда вашу работу хорошо приняли другие учёные.
В жизни, все оказалось гораздо проще и прозаичнее. Я опоздал… Но на сколько! Всего-то навсего 18 лет! Под страшными продолжительными пытками и не с первого раза Гугл признался мне, что эта теорема была опубликована в 1996 году!
Слишком простая теорема — было бы странно, если бы ее только в 1996 году доказали. У меня в школе тоже были подобные "теоремы", хорошо что почти никому о них не рассказывал — сейчас стыдился бы.
Очень круто…
Но на первом курсе матана была формула для сферы в трехмерных координатах
x^2+y^2+z^2=R^2, где R — радиус сферы.
Аналогичным образом ищется большая диагональ параллелепипеда.
Давайте проблематику поднимем на более высокий уровень, и совершим несложное открытие:
Представим, что R — это число Грэмма, насколько многомерным должно быть пространство, чтобы выполнялось приведенное выше выражение?
С этой пирамидой, у которой при одной вершине угол прямой, был курьёз на подготовительных курсах в университет. Уже более 20 лет назад. Задача была в том, чтобы найти объём, зная длину ребра при прямом угле. Все три ребра одинаковы. Решение оказалось банальным, но никто из абитуриентов его не нашёл. До сих пор помню как пример нестандартного мышления
А чего нестандартного? У любой пирамиды объем разве не треть площади основания на высоту?
a^3/2 ?
прикольно, а я только сейчас увидел в геометрическом доказательстве т.Пифагора доказательство выражения
(a+b)(a+b)=a^2+2ab+b^2
кто-нить раньше его уже видел?
: о)
Однако, в вашей интерпретации остаётся совершенно не понятно почему бывают целочисленные четвёрки? Сколько их? И можно ли их как-то описать?
В случае египетских треугольников на все эти вопросы можно дать изящный ответ:
1) Прежде всего переформулируем задачу: мы ищем целые числа a,b,c, т.ч
(a/c)^2+(b/c)^2=1
Иными словами мы ищем рациональные числа x=a/c, y=b/c, т.ч x^2+y^2=1
2) Такие числа — это просто точки на единичной окружности с рациональными координатами
3) Последнее наблюдение (имеющее геометрическую интерпретацию) состоит в том что на окружности можно ввести «рациональную параметризацию»
x=(t^2-1)/(t^2+1), y=(-2t)/(t^2+1), легко проверить что x^2+y^2=1
4) Теперь ясно что любое рациональное число t даёт вам египетский треугольник, более того не сложно доказать что таким способом получаются все египетские треугольники.
Это доказательсто из книжки В.И.Арнольда «геометрия комплексных чисел, кватернионов и спинов», возможно вам, как любопытному человеку она будет интересна.
Соответственно вопрос, можно ли что-то подобное сделать для «египетских четверок», и может ли в этой задаче помочь ваша геометрическая идея.
Эта задача может оказаться весьма нетривиальной и (если помечтать ) связанной и с алгебраической геометрией и с Ферма.
Удачи!
Храм Науки и Техники в Северной Корее
vk.com/album-36928352_248393172
Чтобы понятна была разница — квадрат 8×8 можно разрезать на кусочки и сложить из них прямоугольник 5×13. Но это не доказательство, что 8×8 = 5×13.

Речь о том, что физическая демонстрация не может доказать математическое утверждение, может только навести на мысль.
К рисункам в статье ноль претензий. Я про то, что правильно называть не доказательством, а демонстрацией:

Мы берём квадрат стороной (a + b) — его площадь (a + b)². Площадь внутренних треугольников — a * b / 2. Треугольников 4 штуки. Значит площадь оставшейся части ровно (a + b)² – (a * b / 2) * 4 = a² + 2ab + b² + 2ab = a² + b². Здесь нет никаких «но» — площадь ровно a² + b², причём нам даже не понадобилась вторая картинка.
Но нельзя сказать, что вторая картинка тоже не доказывает — все преобразования, которые были сделаны, строго математические. Например, когда известно, что у нас есть два одинаковых прямоугольных треугольника, то точно известно, что из них можно составить прямоугольник с такими же сторонами, причём когда одна сторона этого прямоугольника равна a, и прямоугольник вложен в квадрат со стороной (a + b), то оставшаяся часть справа — это b. Если высота прямоугольника b, то площадь оставшейся части справа будет равно b (которое мы получили ранее), умноженное на b, что равно b². Именно это и показано на картинке.
Далее раз высота b, а прямоугольник вписан в квадрат стороной (a + b), то оставшаяся высота сверху — a (а ширина a + b). Когда мы убираем такой же прямоугольник с любой из сторон, останется ширина a. Площадь такой оставшейся части будет равна a² (что также показано на картинке). Суммарная площадь оставшихся частей — a² + b² (что и в итоге доказано картинкой).
В Вашем же примере всё наоборот. Во-первых, если чуть поменять форму или размеры фигур, то Ваш пример тут же сваливается (что и происходит). А вот визуальную форму во второй картинке в статье можно менять сколько угодно, т. к. объекты всё-равно описаны математически, и результат a² + b² от этого не изменится. Во-вторых, Вы не только переместили фигуры, но и изменили их форму.
Геометрическое «доказательство» показывает пример ошибки, невидимой на глаз, но обнаружимой математически.
Чтобы установка правильно показала закон — её тоже нужно подгонять под результат и напильником дорабатывать.
О том и речь.
Но: если вы не знаете ничего об истинности утверждений заранее, вы должны сомневаться в обоих случаях.
Пример: в опыте с переливанием жидкости в большом квадрате остаётся пузырё воздуха. Шок, сенсация, теорема Пифагора опровергнута? Возможно. Но геометрия говорит обратное, так что это в установке что-то кривое.
Другой пример: учёные обнаружили нейтрино, двигающиеся быстрее скорости света. Эксперимент проводился максимально добросовестно, настолько точно и аккуратно, насколько возможно. Новая физика? Нет. Но в этом случае учёные сами поставили под вопрос свои результаты, перепроверили и нашли ошибку, которую допустили случайно, не по злому умыслу. А если бы решили не перепроверять — из-за одного подозрения всю физику переписывать?
Третий пример: в воде электроны могут двигаться быстрее света. Верно ли обобщение, что электроны могут двигаться быстрее света в любой среде, включая вакуум?
Проблема экспериментов в другом — в том, что нельзя гарантировать, что исключены все влияющие факторы. Поэтому эксперимент ничего не доказывает в математическом понимании этого слова, а только подтверждает с некоторой вероятностью.
Совершенно согласен, что для математических теорем нет правильных или неправильных экспериментальных доказательств, потому что никакой эксперимент в строгом математическом смысле доказательством быть не может. Правильность или неправильность пришивается, по сути, задним числом, когда теорема доказана строгим математическим способом.
Да, хорошая демонстрация для человека «с улицы» иногда может быть лучше в плане просвещения, чем попытки объяснить строгое доказательство. Но есть и обратная сторона — можно сделать «эксперимент», намеренно вводящий в заблуждение, типа проектов «вечных двигателей». И, объективно говоря, без бэкграунда у человека нет способа отличить добросовестную демонстрацию от жульничества. Из-за чего я и начал холивар «доказательство или нет», хотя какая бы, казалось, разница.
Вы показали, как продемонстрировать правильный закон.
Вам в ответ показали, как продемонстрировать неправильное утверждение.
Вы прицепились к форме демонстрации, а оно тут ни при чём. На установке с переливанием воды тоже может оказаться, что 64 равно 65 с погрешностью, необнаружимой визуально.
То есть у вас есть три примера
1) Абсолютно правильное геометрическое доказательство теоремы пифагора.
2) Физическая демонстрация теоремы пифагора
3) Заведомо неправильно геометрическое построение для доказательства ложного утверждения. (Оно неправильно не потому что оно доказывает ложное утверждение, а потому что утверждает что при соединении трапеции и треугольника получится треугольник, что на самом деле не доказано и очевидно ложно).
Все три примера относятся к совершенно разным категориям.
Абсолютно правильное геометрическое доказательство теоремы пифагора.
?
Во вторых, с чего Вы взяли, что
Все три примера относятся к совершенно разным категориям.
?
А ещё верите, будто бывает что-то «очевидное».
Ответьте, пожалуйста, на мои вопросы. Оба.
2) Рассматриваем геометрическое доказательство теоремы Пифагора в статье. Оно строится на утверждениях:
а) Площадь квадрата равна площади составляющих её треугольников и квадратов.
б) Сумма острых углов прямоугольного треугольника равна 90 градусов.
Разрезая квадрат двумя разными способами, а по нашим теоремам эти разрезания возможны и точны доказываем теорему Пифагора — это строгое математическое доказательство. И ответ на ваш первый вопрос.
3) Что такое физическая демонстрация теоремы Пифагора.
а) Так как теорема Пифагора верна то объемы сосудов будут практически одинаковы (зависит от точности производства сосудов с некоторой погрешностью)
б) Так как существует погрешность производства и измерений данная демонстрация не может являться доказательством. Но она демонстрирует точную теорему.
4) Рассматриваем пример разрезания квадрата 8х8
а) Производим точный разрез квадрата на показаные фигуры.
б) Производим разрезку прямоугольника 5х13, вторым способом.
с) Пытаемся доказать что фигуры с обоих разрезов равны.
д) Не можем это доказать так как они очевидно не равны, для этого нам надо доказать, что соединяемые углы трапеций и треугольников смежные, но мы это не доказали, (потому что они собственно в сумме не дают 180 градусов)
Таким образом мы приходим к выводу что перед нами некорректное геометрическое доказательство, не основанное на логических рассуждениях и теоремах.
5) Получаем три примера:
а) Корректное математическое доказательство теоремы Пифагора.
б) Физическая демонстрация теоемы Пифагора.
в) Некорректное математическое доказательство равенства площади прямоугольника и квадрата.
Очевидно что это три разных категории. Что отвечает на ваш второй вопрос. Вы уверены что знаете что такое математика и формальная логика? Вы даже не потрудились обосновать логически свое утверждение что это все одно и тоже.
2) это доказательство не геометрическое, а логическое. Ещё конкретнее: Вы использовали дедуктивную логику.
3) согласен
4) Вы аналитически доказали неверность равенства указанных прямоугольников. Согласен.
5)
а) Корректное математическое доказательство теоремы Пифагора.
б) Физическая демонстрация теоемы Пифагора.
в) геометрическая демонстрация приблизительного равенства площадей двух треугольников.
Очевидно, что б и в относятся к одному классу.
в — это не приблизительное равенство площадей двух треугольников. Более того там вообще во втором построении нет треугольников. Это ошибочное геометрическое доказательство (примерно из серии доказательств вычисляющих квадратные корни из двух сторон равенства которое математически некорректно)
Именно поэтому это три различных примера.
Вы считаете геометрию (напомню это раздел математики) детскими рисунками?
Геометрические построения не являются необходимой частью этого доказательства. Вы, кстати не сделали ни одного, только описали их словами, однако я всё понял.
в — это не приблизительное равенство площадей двух треугольников.
Да, я оговорился, не треугольников, а прямоугольников.
Это ошибочное геометрическое доказательство
Там нет никакого доказательства, только геометрическая демонстрация. То же самое можно было бы показать на переливающейся воде — ничего бы по сути не изменилось.
Там именно доказывается равенство
Не доказывается, а демонстрируется.
Хватит извиваться и нести чушь.
Хватит упорствовать в своём бреде. Это становится невыносимо.
Определение моё, но по смыслу совпадающее с тем, что мы наблюдаем у Евклида.
точное геометрическое построение
Вы определитесь, с чем Вы работаете. Либо у Вас основа — геометрическое построение, точное настолько, насколько тверда рука чертившего, либо — набор утверждений относительно свойств геометрической фигуры, а построение служит только для иллюстрации.
Либо у Вас основа — геометрическое построение, точное настолько, насколько тверда рука чертившего, либо — набор утверждений относительно свойств геометрической фигуры, а построение служит только для иллюстрации.
А Вы упорно не хотите проанализировать то, что называете «геометрическим доказательством». Более того, даже лично изложив его словами без единого построения, всё равно упорствуете в том, что оно геометрическое. Феноменально.
Что значит проанализировать, то что называю «геометрическим доказательством»? Проанализировать можно само доказательство. А что вы хотите проанализировать?
И я нигде не доказывал его без построения.
2) Рассматриваем геометрическое доказательство теоремы Пифагора в статье. Оно строится на утверждениях:
а) Площадь квадрата равна площади составляющих её треугольников и квадратов.
б) Сумма острых углов прямоугольного треугольника равна 90 градусов.
Разрезая квадрат двумя разными способами, а по нашим теоремам эти разрезания возможны и точны доказываем теорему Пифагора — это строгое математическое доказательство. И ответ на ваш первый вопрос.
Это единственно место которое вы бы могли назвать доказательством без построения (что только показывает ваше незнание математики). И оно не может доказать теорему так как в нём не указан способ разрезания квадратов (так как они указаны на геометрическом построении).
А мою просьбу указать что вы подразумеваете под демонстрацией вы уже упорно игнорируете уже в третий раз, так как видимо не имеете об этом никакого соображения.
5) Получаем три примера:
а) Корректное математическое доказательство теоремы Пифагора.
б) Физическая демонстрация теоремы Пифагора.
в) Некорректное математическое доказательство равенства площади прямоугольника и квадрата.
Для справки: в случае в) я предлагаю изготовить квадрат 8×8 из реального материала и разрезать, как показано на рисунке, затем переложить куски, как показано на втором рисунке.
Именно для того, чтобы это было не некорректным математическим доказательством, а вводящей в заблуждение физической демонстрацией.
При рассмотрении такой демонстрации возможны две интерпретации (предполагая, что формулы для площади прямоугольников нам неизвестны):
1) Площади квадрата и прямоугольника равны, а небольшие щели после перекладывания — это погрешность разрезания.
2) Площади квадрата и прямоугольника не равны, и щели это демонстрируют.
И в этом случае варианты б) и в) становятся равнозначными в плане того, что это физические демонстрации математических утверждений, истинность которых, в конечном итоге, устанавливается только путём логических рассуждений. О чём Zenitchik и я и толкуем.
Если бы Вам было необходимо измерять стороны фигуры с помощью измерительного инструмента — анализировать его было бы не просто.
А что показывает разрезание одного ничем не примечательного четырехугольника и складывание из него другого ничем не примечательного другого четырехугольника?
Что их площади примерно равны. Ни больше, ни меньше.
А Вы — юлите. До сих пор ни Вы, ни ваши оппоненты про важность демонстрируемого утверждения не писали. Теперь Вы решили написать. Значит, без привлечения этого фактора Ваша позиция не подтверждается.
И что нам даёт равенство двух ничем не примечательных прямоугольников? Они даже ни какому классу не принадлежат просто два прямоугольника равной площади. Зачем нам показывать что они равны? Вот в доказательстве теоремы Пифагора равенство квадратов доказывает теорему. В примере с квадратом 8х8 и прямоугольником 5х13 пытаемся неправильно доказать что они равны. А что даёт нам разрезание неизвестно какого прямоугольника и собирание из него неизвестно какого другого прямоугольника?
Мало того что математику не знаете так еще и демагогией занимаетесь. Сначала обсуждаете точные прямоугольники с известными сторонами и вдруг они волшебно у вас превращаются в просто произвольные.
А в указанном примере с перетекающей жидкостью сумма площадей квадратов, построенных на катетах, точно соответствует квадрату, построенному на гипотенузе — жидкость либо несжимаема, либо в ней нет разрывов.
А так — хорошая, годная демонстрация. Понять её для многих проще, чем математическое доказательство. Но доказательством её это не делает.
Однажды, один преподователь института посоветовал порыться в математической энциклопедии. И, горе мне! Нашёл в ней некоего немца (фамилию забыл), который это придумал раньше меня лет на 300! Правда, формула-определение у него была другая — мне совершенно не понятная: через интеграл с кружочком. Вот такие дела.
Когда рассказывал про эти производные, то почти все однокурсники по университету смеялись: это как же получается — дробная производная от константы не равна нулю?
Тоже о таком задумывался, однако через некоторое время нашел материал по таким производным.
Нашёл в ней некоего немца (фамилию забыл), который это придумал раньше меня лет на 300! Правда, формула-определение у него была другая — мне совершенно не понятная: через интеграл с кружочком.
Вот статья в википедии, которая описывает и производные и интегралы и другие вещи дробного порядка: https://en.wikipedia.org/wiki/Fractional_calculus
Правда, возлагал надежды на другую свою разработку: формулу-определение для производных дробного порядка.
Вычисляется с использованием гамма-функции: Fractional derivative of a basic power function.
Если кому то будет интересно, то за недели две смогу восстановить формульно и с примерами.
Рад за вас, желаю дальнейших открытий и озарений!
3^2+4^2=5^2
Увидел что для степени 3:
3^3+4^3+5^3=6^3 (это так)
Обрадовался, думал что и для всех степеней это работает. Потом проверил для степени 4 — обломился и понял что просто случайно так совпало для 3, для остальных чисел не работает.
12+42+82=92Вот тут меня цепляет не равенство суммы квадратов, а то, что на выходе в квадрат возводится простое число (не во всех случаях, но первый случай сам по себе интересен — 1, 4 и 8 — степень двойки и на выходе получается 34.). Есть что почитать на эту тему?
22+32+62=72
32+42+122=132
42+52+202=212
62+132+182=232
Во 2, 3 и 4 примере — первые два возводимые в квадрат числа являются произведением для третьего, что тоже подозрительно.
В 5 примере такого нет, поскольку второе число — простое. Но если из него вычесть 10, то получим 6*3=18. Но, возможно, я просто на ограниченной выборке ищу какие-то закономерности, которых нет на достаточно большом множестве таких четвёрок.
21 — тоже не простое, так что, вероятно, это обманка.
Зато мне сразу бросилось в глаза другое (если посмотреть чуть дальше, чем вы описали):
2^2+3^2+6^2=7^2
3^2+4^2+12^2=13^2
4^2+5^2+20^2=21^2
Т.е. видно, что
n^2 + (n+1)^2 + (n(n+1))^2 = (n(n+1)+1)^2
Сразу же проверил
5^2+6^2+30^2=31^2
15^2+16^2+240^2=241^2
Ура, я первооткрыватель!
Это примерно так же весело и бесполезно, как школьное наблюдение, что при умножении однозначного чётного числа на 6 получается двухзначное, последняя цифра которого то самое чётное число.
Сразу же проверилМожно было просто раскрыть скобки.
www.youtube.com/watch?v=G3BhQx1Y5E0
www.youtube.com/watch?v=pHRr3axkrmw
Главное, не пугаться страшных слов, их совсем немного
>Знали ли вы эту теорему до прочтения статьи?
под словом «эту» вы имеете ввиду теорему Пифагора или де Гуа?
www.youtube.com/watch?v=_GptmtLIh5A

ЗЫ: а как размещать видео в комментариях?
А так, задача, приведенная вами, тянет лишь на задачу со звездочкой из учебника Погорелова.
Всем добра!
Но вы зря отказываетесь почитать «Лекции об икосаэдре и решении уравнений пятой степени» (Клейна). Вы дотошный раз так долго вам не давала покоя данная теорема. А у Клейна при прочтении как раз такая дотошность и требуется. Начните читать и перед вами откроется крайне интересный мир прикладной математики и ее проблем.
В ТФКП (это на много легче) вам будут интересны конформные отображения и вообще работа с комплексными переменными.
Вот яркий пример: начертите параболу у=х*х и прямую у=к*х в декартовой системе. Теперь проводите вертикальные прямые и вы увидите, что одной точке прямой соответствует строго одна точка параболы, то есть можно составить функцию (функционал), устанавливающий взаимно однозначное соответствие между прямой и параболой. Легко? Да. Перейдем дальше.
Возьмите ось «х»-теперь это ваша прямая и нарисуйте окружность с центром в начале координат (или чтобы прямая была касательной к окружности снизу). Возьмите верхнюю точку окружности (и только ее!!! для упрощения) и любую точку на прямой. Получите 2 точки. Соедините их другой прямой. И снова вы увидите, что можно сделать так чтобы каждой точке окружности соответствовала строго одна точка прямой. (такую функцию можно составить с помощью комплексных переменных).
А теперь интрига.
Для точки +бесконечность и -бесконечность на прямой будет соответствовать только одна (верхняя точка окружности). То есть прямая (в ТФКП) — окружность с бесконечным радиусом.
Преобразование 1/z в ТФКП выворачивает единичную окружность наизнанку. То есть что-то конечное и понятное становится бескрайним.
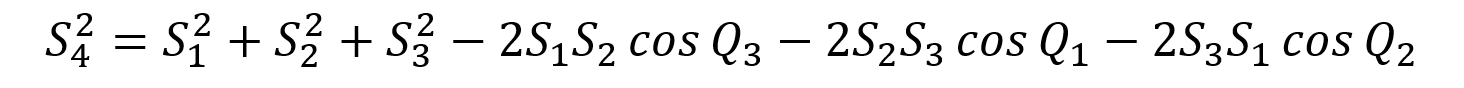
Малоизвестное обобщение теоремы Пифагора