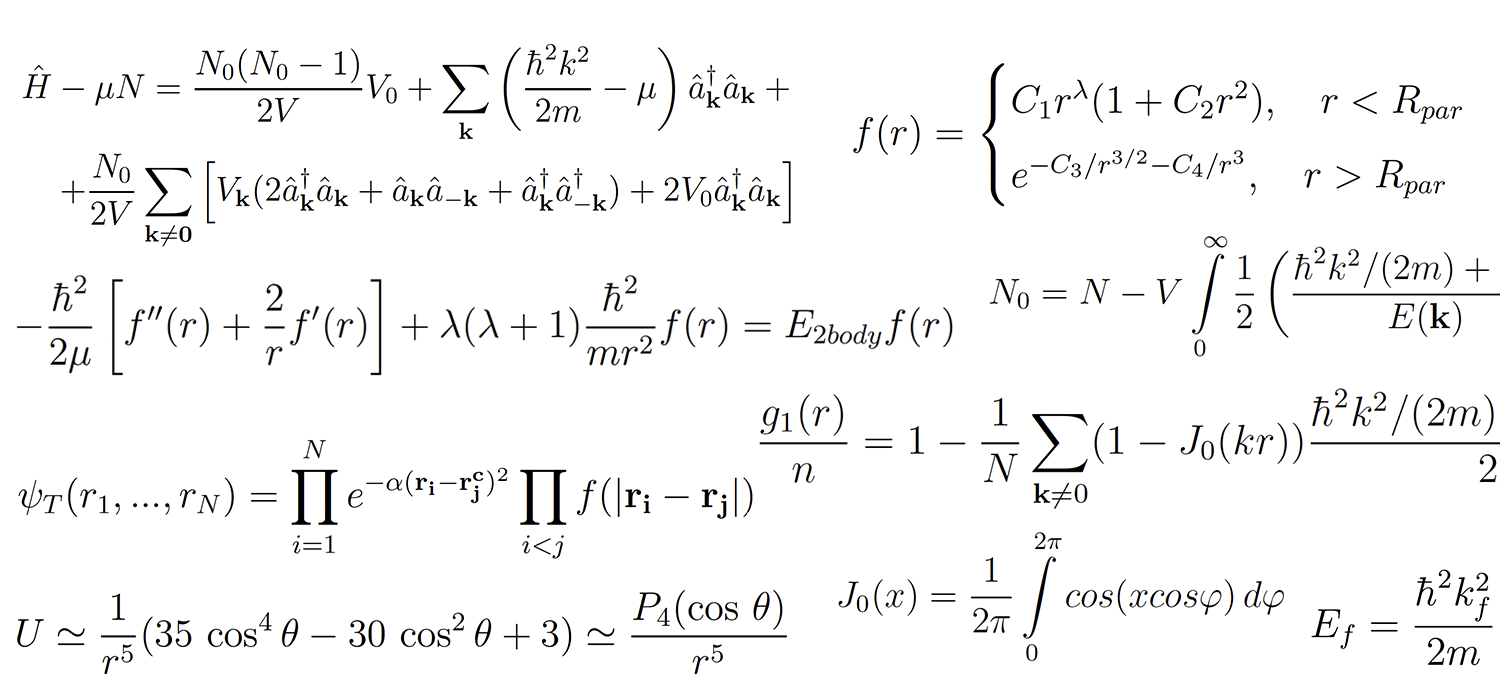
Моя специальность — физика конденсированного состояния. Разумеется, в процессе погружения в нее требуется изучать много научных статей, однако на разбор хотя бы одной может уйти немало времени. На arxiv в разделе cond-mat публикуется более тысячи статей в месяц. Складывается ситуация, когда многие исследователи, особенно начинающие, не обладают целостным видением своей области науки. Описанный в этой статье инструмент резюмирует содержимое базы научных статей и призван ускорить работу с литературой.
Стоит оговориться, что мы изобретаем велосипед, вот только наш будет ездить бесплатно (цены на платные аналоги настолько неприличные, что их не принято указывать).
Велосипед будет собран на Python, для тематического моделирования используется Gensim, для визуализации Plot.ly. В конце статьи приводятся ссылки на Jupyter-ноутбуки и GitHub.
Исходный материал для работы — аннотации и тексты научный статей. Если первые нам доступны в «готовом» XML виде, то PDF файлы статей нужно конвертировать в txt, в результате этого процесса в текстах остается много «мусора», поэтому их необходимо серьезно почистить.
Образец аннотации
<?xml version="1.0" encoding="UTF-8"?>
<feed xmlns="http://www.w3.org/2005/Atom">
<link href="http://arxiv.org/api/query?search_query%3D%26id_list%3D1706.09062%26start%3D0%26max_results%3D10" rel="self" type="application/atom+xml"/>
<title type="html">ArXiv Query: search_query=&id_list=1706.09062&start=0&max_results=10</title>
<id>http://arxiv.org/api/ECEwpFhuO79sa+LzMzx6/iStFak</id>
<updated>2018-05-01T00:00:00-04:00</updated>
<opensearch:totalResults xmlns:opensearch="http://a9.com/-/spec/opensearch/1.1/">1</opensearch:totalResults>
<opensearch:startIndex xmlns:opensearch="http://a9.com/-/spec/opensearch/1.1/">0</opensearch:startIndex>
<opensearch:itemsPerPage xmlns:opensearch="http://a9.com/-/spec/opensearch/1.1/">10</opensearch:itemsPerPage>
<entry>
<id>http://arxiv.org/abs/1706.09062v1</id>
<updated>2017-06-27T22:03:24Z</updated>
<published>2017-06-27T22:03:24Z</published>
<title>On Bose-Einstein condensation and superfluidity of trapped photons with
coordinate-dependent mass and interactions</title>
<summary> The condensate density profile of trapped two-dimensional gas of photons in
an optical microcavity, filled by a dye solution, is analyzed taking into
account a coordinate-dependent effective mass of cavity photons and
photon-photon coupling parameter. The profiles for the densities of the
superfluid and normal phases of trapped photons in the different regions of the
system at the fixed temperature are analyzed. The radial dependencies of local
mean-field phase transition temperature $T_c^0 (r)$ and local
Kosterlitz-Thouless transition temperature $T_c (r)$ for trapped microcavity
photons are obtained. The coordinate dependence of cavity photon effective mass
and photon-photon coupling parameter is important for the mirrors of smaller
radius with the high trapping frequency, which provides BEC and superfluidity
for smaller critical number of photons at the same temperature.
We discuss a possibility of an experimental study of the density profiles for
the normal and superfluid components in the system under consideration.
</summary>
<author>
<name>Oleg L. Berman</name>
</author>
<author>
<name>Roman Ya. Kezerashvili</name>
</author>
<author>
<name>Yurii E. Lozovik</name>
</author>
<arxiv:doi xmlns:arxiv="http://arxiv.org/schemas/atom">10.1364/JOSAB.34.001649</arxiv:doi>
<link title="doi" href="http://dx.doi.org/10.1364/JOSAB.34.001649" rel="related"/>
<arxiv:comment xmlns:arxiv="http://arxiv.org/schemas/atom">14 page 5, figures</arxiv:comment>
<link href="http://arxiv.org/abs/1706.09062v1" rel="alternate" type="text/html"/>
<link title="pdf" href="http://arxiv.org/pdf/1706.09062v1" rel="related" type="application/pdf"/>
<arxiv:primary_category xmlns:arxiv="http://arxiv.org/schemas/atom" term="cond-mat.mes-hall" scheme="http://arxiv.org/schemas/atom"/>
<category term="cond-mat.mes-hall" scheme="http://arxiv.org/schemas/atom"/>
</entry>
</feed>
Образец текста
On Bose-Einstein condensation and superfluidity of trapped photons with
coordinate-dependent mass and interactions
Oleg L. Berman1,2, Roman Ya. Kezerashvili1,2, and Yurii E. Lozovik3,4
1Physics Department, New York City College of Technology, The City University of New York,
2The Graduate School and University Center, The City University of New York,
Brooklyn, NY 11201, USA
3Institute of Spectroscopy, Russian Academy of Sciences, 142190 Troitsk, Moscow, Russia
4National Research University Higher School of Economics, Moscow, Russia
New York, NY 10016, USA
(Dated: June 29, 2017)
The condensate density profile of trapped two-dimensional gas of photons in an optical micro-
cavity, filled by a dye solution, is analyzed taking into account a coordinate-dependent effective
mass of cavity photons and photon-photon coupling parameter. The profiles for the densities of the
superfluid and normal phases of trapped photons in the different regions of the system at the fixed
temperature are analyzed. The radial dependencies of local mean-п¬Ѓeld phase transition temperature
T 0
c (r) and local Kosterlitz-Thouless transition temperature Tc(r) for trapped microcavity photons
are obtained. The coordinate dependence of cavity photon effective mass and photon-photon cou-
pling parameter is important for the mirrors of smaller radius with the high trapping frequency,
which provides BEC and superfluidity for smaller critical number of photons at the same temper-
ature. We discuss a possibility of an experimental study of the density profiles for the normal and
superfluid components in the system under consideration.
Key words: Photons in a microcavity; Bose-Einstein condensation of photons; superfluidity of
photons.
PACS numbers: 03.75.Hh, 42.55.Mv, 67.85.Bc, 67.85.Hj
I.
INTRODUCTION
When a system of bosons is cooled to low temperatures, a substantial fraction of the particles spontaneously occupy
the single lowest energy quantum state. This phenomenon is known as Bose-Einstein condensation (BEC) and its
occurs in many-particle systems of bosons with masses m and temperature T when the de Broglie wavelength of the
Bose particle exceeds the mean interparticle distance [1]. The most remarkable consequence of BEC is that there
should be a temperature below which a finite fraction of all the bosons “condense” into the same one-particle state
with macroscopic properties described by a single condensate wavefunction, promoting quantum physics to classical
time- and length scales.
Most recently, the observations at room temperature of the BEC of two-dimensional photon gas confined in an optical
microcavity, formed by spherical mirrors and filled by a dye solution, were reported [2–5]. The interaction between
microcavity photons is achieved through the interaction of the photons with the non-linear media of a microcavity,
п¬Ѓlled by a dye solution. While the main contribution to the interaction in the experiment, reported in Ref. 2, is
thermooptic, it is not a contact interaction.
It is known that BEC for bosons can exist without particle-particle
interactions [6] (see Ref. 1 for the details), but at least the interactions with the surrounding media are necessary to
achieve thermodynamical equilibrium. For photon BEC it can be achieved by interaction with incoherent phonons [7].
The influence of interactions on condensate-number fluctuations in a BEC of microcavity photons was studied in Ref. 8.
The kinetics of photon thermalization and condensation was analyzed in Refs. 9–11. The kinetics of trapped photon
gas in a microcavity, п¬Ѓlled by a dye solution, was studied, and, a crossover between driven-dissipative system laser
dynamics and a thermalized Bose-Einstein condensation of photons was observed [12].
In previous theoretical studies the equation of motion for a BEC of photons confined by the axially symmetrical
trap in a microcavity was obtained.
It was assumed that the changes of the cavity width are much smaller than
the width of the trap [13]. This assumption results in the coordinate-independent effective photon mass mph and
photon-photon coupling parameter g. In this Paper, we study the local superfluid and normal density profiles for
trapped two-dimensional gas of photons with the coordinate-dependent effective mass and photon-photon coupling
parameter in a an optical microcavity, п¬Ѓlled by a dye solution. We propose the approach to study the local BEC
and local superfluidity of cavity photon gas in the framework of local density approximation (LDA) in the traps of
larger size without the assumption, that total changes of the cavity width are much smaller than the size of the trap.
In this case, we study the effects of coordinate-dependent effective mass and photon-photon coupling parameter on
the superfluid and normal density profiles as well as the profiles of the local temperature of the phase transition for
trapped cavity photons. Such approach is useful for the mirrors of smaller radius with the high trapping frequency,
2
which provide BEC and superfluidity for smaller critical number of photons at the same temperature.
The paper is organized in the following way.
In Sec. II, we obtain the condensate density profile for trapped
microcavity photon BEC with locally variable mass and interactions. The expression for the number of particles in a
condensate is analyzed in Sec. III. In Sec. IV, the dependence of the condensate parameters on the geometry of the
trap is discussed. In Sec. V, we study the collective excitation spectrum and superfluidity of 2D weakly-interacting
Bose gas of cavity photons. The results of our calculations are discussed in Sec. VI. The proposed experiment for
measuring the distribution of the local density of a photon BEC is described in Sec. VII. The conclusions follow in
Sec. VIII.
II. THE CONDENSATE DENSITY PROFILE
While at finite temperatures there is no true BEC in any infinite untrapped two-dimensional (2D) system, a true
2D BEC quantum phase transition can be obtained in the presence of a confining potential [14, 15]. In an infinite
translationally invariant two-dimensional system, without a trap, superfluidity occurs via a Kosterlitz−Thouless
superfluid (KTS) phase transition [16]. While KTS phase transition occurs in systems, characterized by thermal
equilibrium, it survives in a dissipative highly nonequilibrium system driven into a steady state [17].
The trap for the cavity photons can be formed by the concave spherical mirrors of the microcavity, that provide
the axial symmetry for a trapped gas of photons. Thus the transverse (along xy plane of the cavity) confinement
of photons can be achieved by using an optical microcavity with a variable width. Let us introduce the frame of
reference, where zв€’axis is directed along the axis of cavity mirrors, and (x, y) plane is perpendicular to this axis. The
energy spectrum E(k) for small wave vectors k of photons, confined in z direction in an ideal microcavity with the
coordinate-dependent width L(r), is given by [2]
E(k) =
ВЇhПЂcЛњn
...
[23] L. Onsager, “Statistical Hydrodynamics,” Nuovo Cimento Suppl. 6, 279 (1949).
[24] R. P. Feynman, “Application of Quantum Mechanics to Liquid Helium,” Prog. Low Temp. Phys. 1, 17 (1955).
[25] P. C. Hohenberg and P. C. Martin, “Microscopic Theory of Superfluid Helium,” Ann. Phys. 34, 291 (1965).
[26] G. Blatter, M. Y. FeigelвЂman, Y. B. Geshkenbein, A. I. Larkin, and V. M. Vinokur, “Vortices in high-temperature super-
conductors,” Rev. Mod. Phys. 66, 1125 (1994).
[27] N. S. Voronova and Yu. E. Lozovik, “Excitons in cores of exciton-polariton vortices,” Phys. Rev. B 86, 195305 (2012);
N. S. Voronova, A. A. Elistratov, and Yu. E. Lozovik, “Detuning-Controlled Internal Oscillations in an Exciton-Polariton
Condensate,” Phys. Rev. Lett. 115, 186402 (2015) .
[28] A. Griffin, “Conserving and gapless approximations for an inhomogeneous Bose gas at finite temperatures,” Phys. Rev. B
53, 9341 (1996).
[29] A. A. Abrikosov, L. P. Gorkov and I. E. Dzyaloshinski, Methods of Quantum Field Theory in Statistical Physics (Prentice-
Hall, Englewood Cliffs. N.J., 1963).
[30] O. L. Berman, Yu. E. Lozovik, and D. W. Snoke, “Theory of Bose-Einstein condensation and superfluidity of two-
dimensional polaritons in an in-plane harmonic potential,” Phys. Rev. B 77, 155317 (2008).
[31] O. L. Berman, R. Ya. Kezerashvili, and K. Ziegler, “Superfluidity and collective properties of excitonic polaritons in gapped
graphene in a microcavity”, Phys. Rev. B 86, 235404 (2012).
[32] A. Amo, J. Lefr`ere, S. Pigeon, C. Adrados, C. Ciuti, I. Carusotto, R. Houdr´e, E. Giacobino, and A. Bramati, “Superfluidity
of polaritons in semiconductor microcavities,” Nature Physics 5, 805 (2009).
[33] J. P. Fern´andez and W. J. Mullin, “The Two-Dimensional Bose−Einstein Condensate,” J. Low. Temp. Phys. 128, 233
Из аннотаций нам потребуется информация только об авторах и подразделах статей.
Ниже, в качестве примера, рассмотрен массив статей из раздела cond-mat за 2017-й год. Все описанное легко воспроизвести для любой другой секции.
Самое простое, с чего можно начать исследование текстов — составить список интересующих нас ключевых слов и подсчитать долю статей, в которых они встречаются.

Оценим изменение доли, например, по сравнению с 2010-м годом.
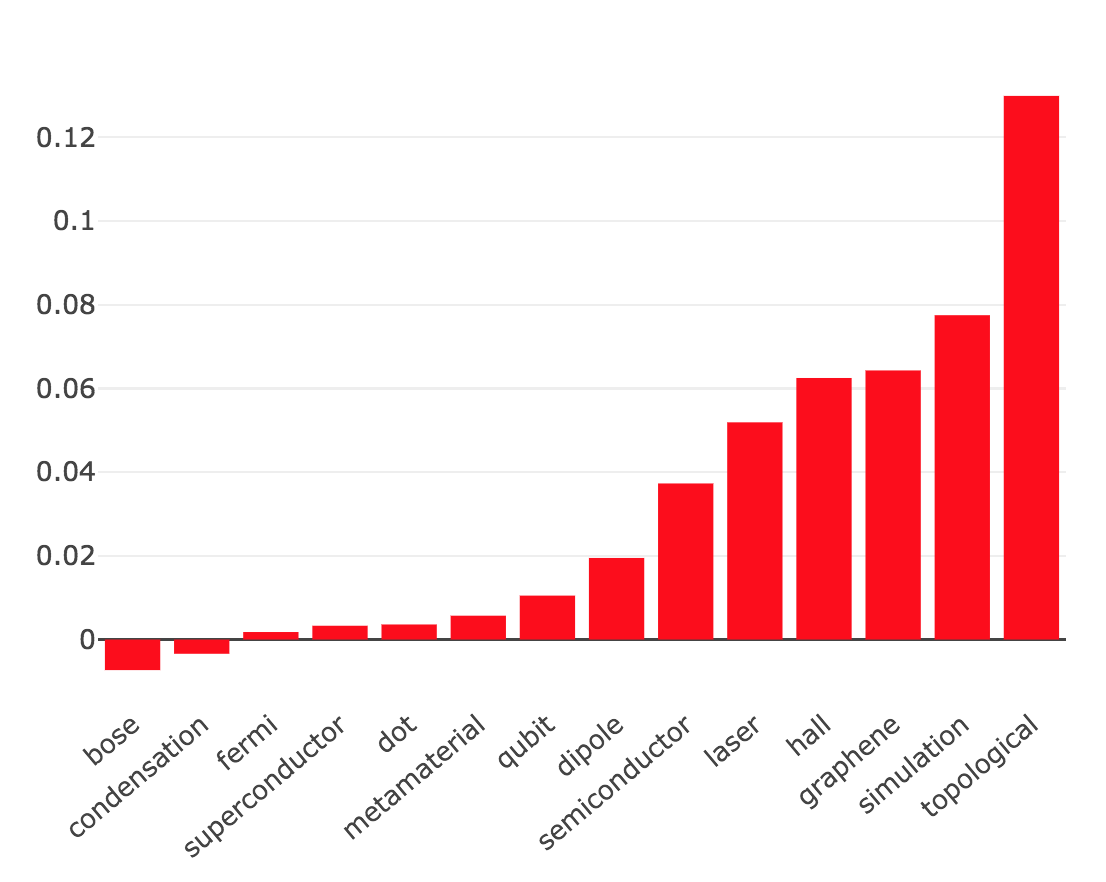
Разница долей за 2017-й и 2010-й гг. (прим.: нобелевская премия по физике в 2016-м году вручена за исследование топологических фаз материи)
Далее, по содержимому текстов строим word2vec модель (для визуализации лучше взять окно пошире, 20 слов). Для каждого ключа берем N ближайших соседей и с помощью t-SNE вычисляем их 2D координаты. Смотрим, как ключевые слова соотносятся друг с другом:

Облако ключевых слов и их сателлитов, N=100. Чем дальше находится N-й сосед, тем больше выделено слово. Релевантные пары: Graphene+Semiconductor, Qubit+Dot, Topological+Hall, Bose+Condensation
На arxiv для каждого раздела есть подразделы. Узнаем, в каких именно подразделах встречаются ключевые слова:
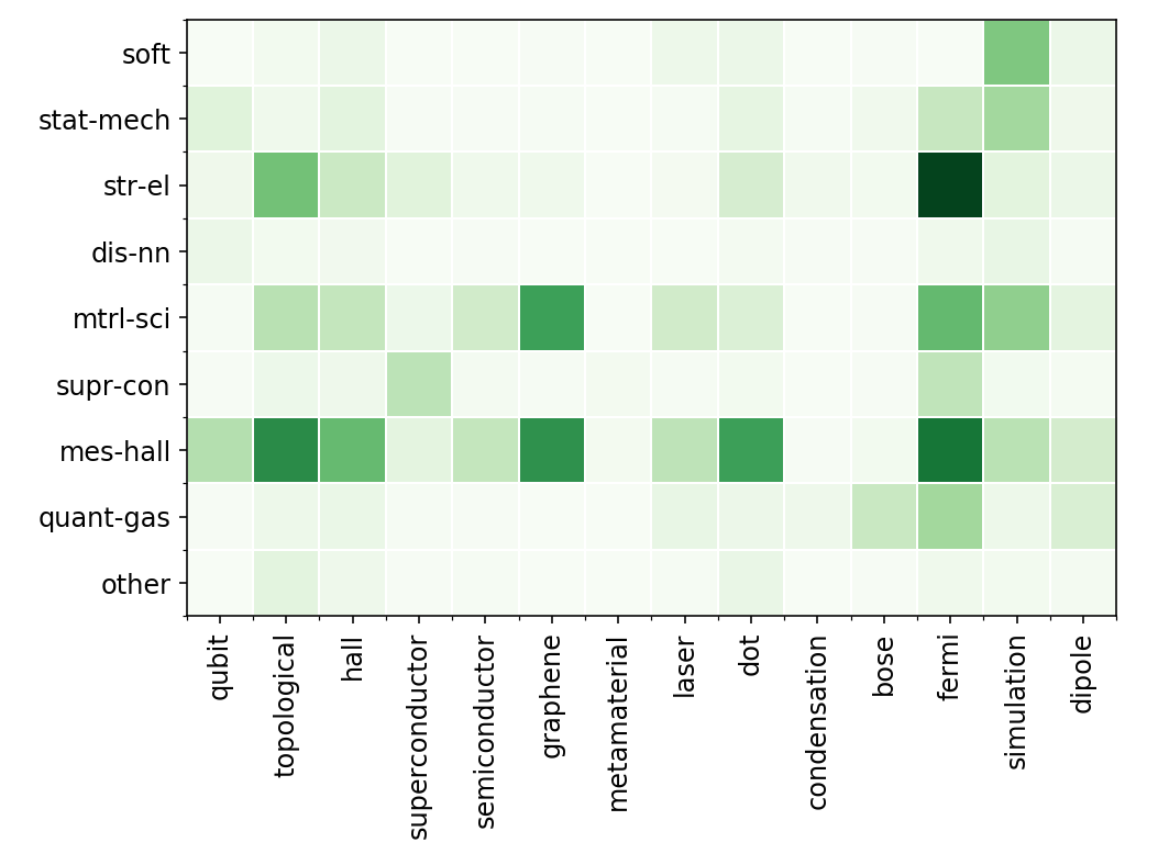
Расшифровка названий подразделов cond-mat
Выше описана работа с набором ключевых слов, который требуется составить вручную, однако какие-то темы могли быть пропущены. Построим LDA модель и посмотрим на топики:

Для каждого топика получим список соответствующих ему статей:
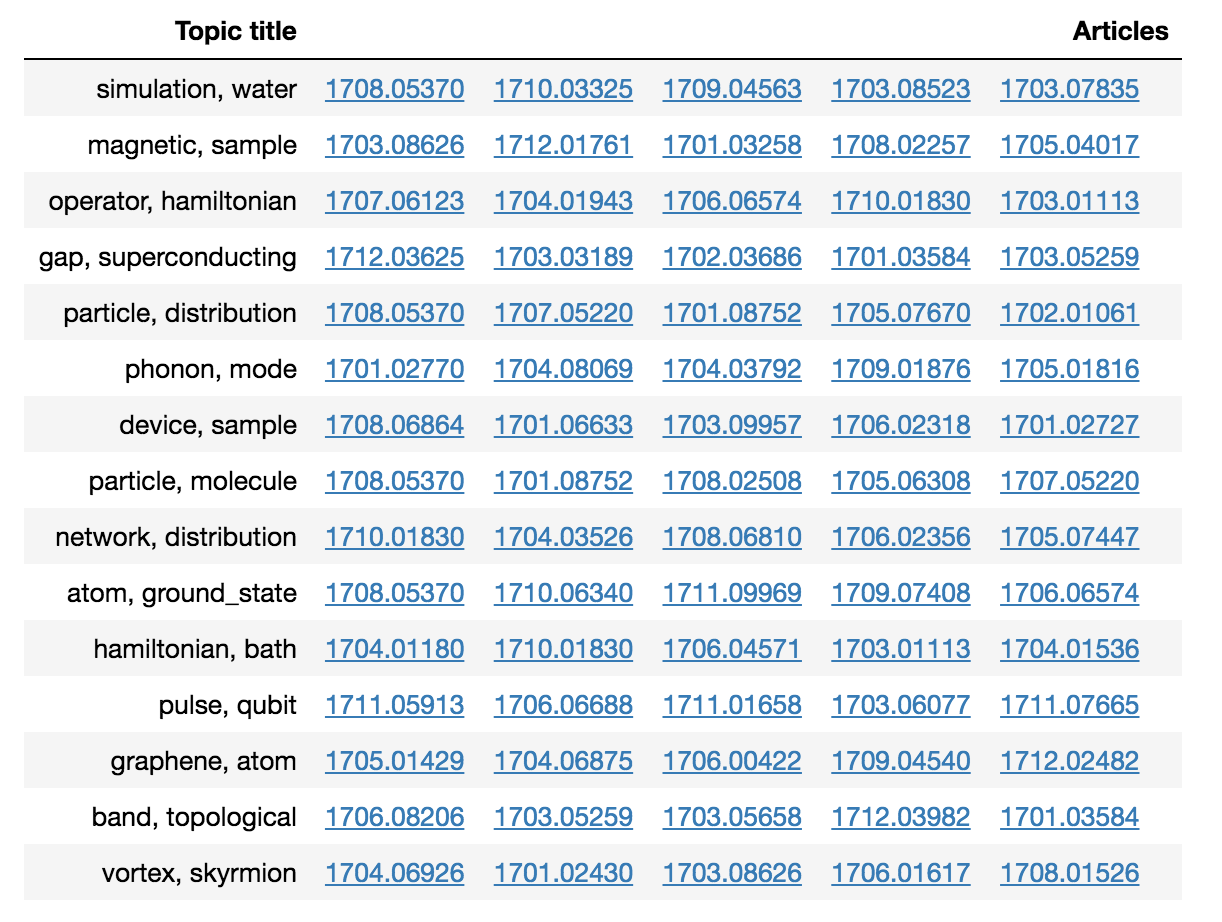
Как известно, при чтении статей всегда полезно изучить ссылки. Можем ли мы собрать какую-то информацию о них? Можем! Посмотрим на «хвост» текста.
Хвост
[23] L. Onsager, “Statistical Hydrodynamics,” Nuovo Cimento Suppl. 6, 279 (1949).
[24] R. P. Feynman, “Application of Quantum Mechanics to Liquid Helium,” Prog. Low Temp. Phys. 1, 17 (1955).
[25] P. C. Hohenberg and P. C. Martin, “Microscopic Theory of Superfluid Helium,” Ann. Phys. 34, 291 (1965).
[26] G. Blatter, M. Y. FeigelвЂman, Y. B. Geshkenbein, A. I. Larkin, and V. M. Vinokur, “Vortices in high-temperature super-
conductors,” Rev. Mod. Phys. 66, 1125 (1994).
[27] N. S. Voronova and Yu. E. Lozovik, “Excitons in cores of exciton-polariton vortices,” Phys. Rev. B 86, 195305 (2012);
N. S. Voronova, A. A. Elistratov, and Yu. E. Lozovik, “Detuning-Controlled Internal Oscillations in an Exciton-Polariton
Condensate,” Phys. Rev. Lett. 115, 186402 (2015) .
[28] A. Griffin, “Conserving and gapless approximations for an inhomogeneous Bose gas at finite temperatures,” Phys. Rev. B
53, 9341 (1996).
[29] A. A. Abrikosov, L. P. Gorkov and I. E. Dzyaloshinski, Methods of Quantum Field Theory in Statistical Physics (Prentice-
Hall, Englewood Cliffs. N.J., 1963).
[30] O. L. Berman, Yu. E. Lozovik, and D. W. Snoke, “Theory of Bose-Einstein condensation and superfluidity of two-
dimensional polaritons in an in-plane harmonic potential,” Phys. Rev. B 77, 155317 (2008).
[31] O. L. Berman, R. Ya. Kezerashvili, and K. Ziegler, “Superfluidity and collective properties of excitonic polaritons in gapped
graphene in a microcavity”, Phys. Rev. B 86, 235404 (2012).
[32] A. Amo, J. Lefr`ere, S. Pigeon, C. Adrados, C. Ciuti, I. Carusotto, R. Houdr´e, E. Giacobino, and A. Bramati, “Superfluidity
of polaritons in semiconductor microcavities,” Nature Physics 5, 805 (2009).
[33] J. P. Fern´andez and W. J. Mullin, “The Two-Dimensional Bose−Einstein Condensate,” J. Low. Temp. Phys. 128, 233
Конвертер PDF хорошо обрабатывает раздел с библиографией. Это означает, что ссылки можно извлечь с помощью нескольких регулярных выражений. В результате получим список часто цитируемых, must-read, статей.

Проверим эти ссылки в Google Scholar:
- Pedrew, Burke, Ernzenhof, 1996 ~85 тыс. цитирований
- Hasan, Kane, 2010 ~10 тыс. цитирований
- Kresse, Furthmüller, 1996 ~44 тыс. цитирований
- Kresse, Joubert, 1999 ~33 тыс. цитирований
Составим список наиболее активных авторов для каждого подраздела — извлечем и подсчитаем содержимое тега author из аннотаций. Число опубликованных конкретным автором статей — характеристика понятная, но ненадежная, ее можно дополнить медианой числа соавторов (см. ноутбуки).
Авторы из mes-hall вне конкуренции: их средний темп работы — больше одной статьи в неделю...
Напоследок оценим долю подразделов:
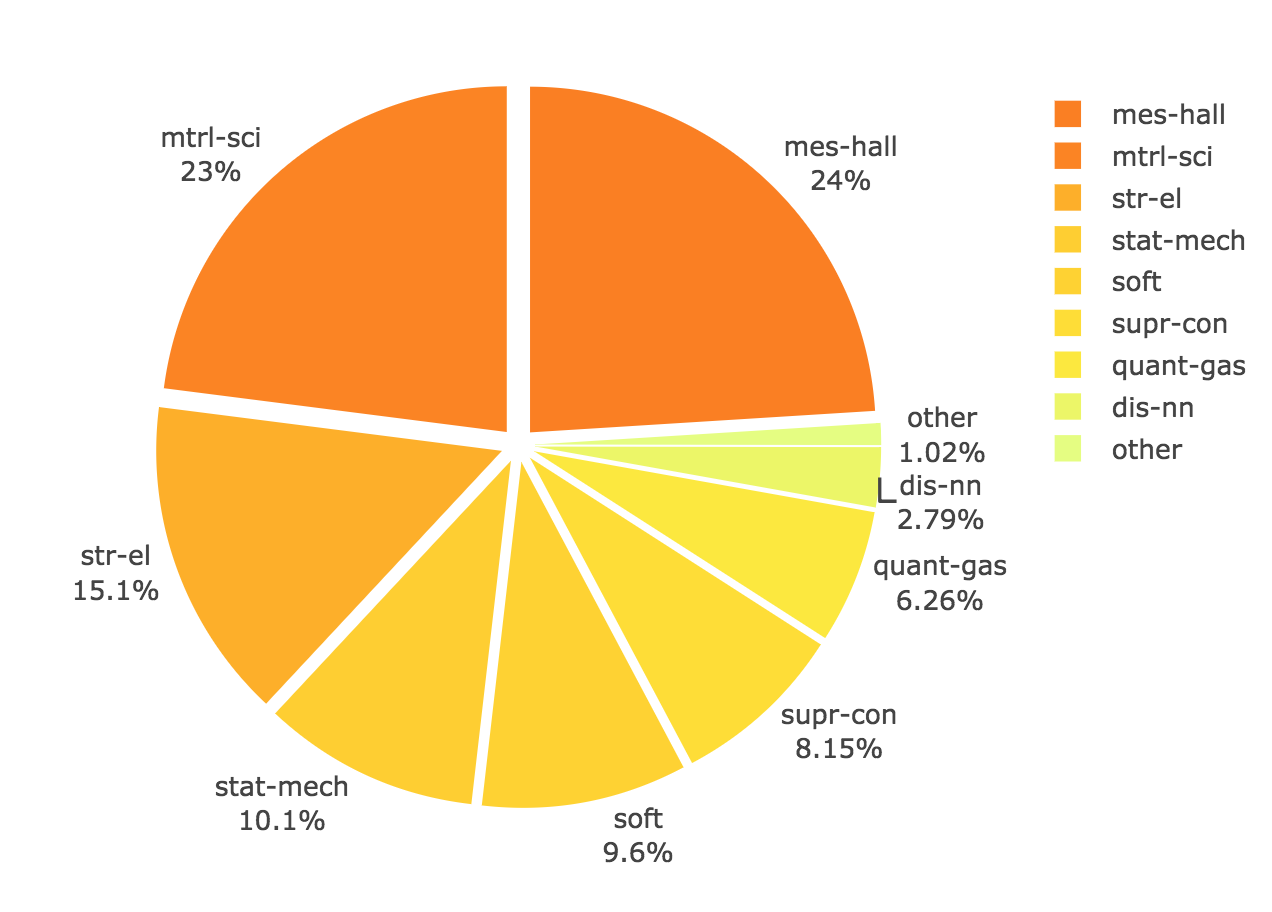
Демо-ноутбуки: cond-mat.17, astro-ph.17, cs.17, math.17
GitHub: ilovescience