Even as I am posting this, I can see that my previous post received a hundred and twenty plus views, but no comments yet. I am saying again that my pursuit is not to give an answer, but to ask a question. I only wonder if there is in fact no answer to the questions I am asking – but anyway, I will continue asking them. If you know how to deal with the problems I am setting – or happen to understand they are not problems at all, I will be most grateful for a constructive input in the comments section. I am sorry to say I was unable to make this post sound as light and unpretentious as the previous one. This one deals with harder questions, is a little wordy, and requires at least elementary knowledge of calculus to be read properly.
In my previous post we discussed the ‘Galilean’ velocity composition used for introduction or substantiation of relative simultaneity. It is not the only point where Einstein resorts to sums c + v or c – v: he does that actually to deduce the Lorentz transforms, notwithstanding the fact that a corollary of the Lorentz transforms is a different velocity composition which makes the above sums null and void. It looks like the conclusions of this deduction negate its premises – but this is not the only strange thing about Einstein’s deduction of the Lorentz transforms undertaken by him in his famous 1905 article.
In Paragraph 3 of that paper Einstein is considering the linear function τ (the time of the reference frame in motion) of the four variables x′ = x – vt, y, z, and t (the three spatial coordinates and time of the frame of reference at rest) and eventually derives a relation between the coefficients of this linear function.
He starts with the definition of τ as of ‘a summary of the data of synchronized clocks’ (p. 6), whence

should hold ‘according to the rule given in §1’ (p. 6), where tau sub zero, tau sub one and tau sub two are the moments when light traveling along the x' axis is respectively emitted at 0, reflected back at x', and returns to 0. Then Einstein re-writes Expression (1) substituting arguments of τ for its indices
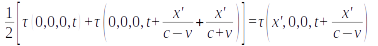
which, granting that

(i. e. τ is understood to be a linear function of four variables where the variables y and z can be omitted as fixed and equal to zero, and q is a certain constant), yields

or

There’s something else exceedingly odd about this way of reasoning apart from already mentioned sums of the velocity of light and that of the frame of reference which, if Einstein’s composition of velocities is true, should not exist.
I must confess it took me some time to figure out what it was that struck me as strange in the transition from (1) to (2). I felt it at once, but the essence and meaning of this oddity was not immediately obvious.
By the definition of relative simultaneity (p. 5) it follows that the clocks which are synchronized in one frame of reference should be unsynchronized in some other, since the readings of a multitude of synchronized clocks are nothing else but a series of simultaneous events. Relativity of simultaneity by right should be referred to as ambiguity of being synchronized, and in these terms it does not make sense to call clocks synchronized without specifying the frame of reference. Clocks of the moving frame of reference as observed ‘from within’ and the same clocks observed ‘from without’ are therefore two different sets. In other words, if (1) is true in one frame of reference, it cannot be true in another.
Recalling the relativity of simultaneity experiment, the test of simultaneity is either a success or a failure depending on the observer.
Which frame of reference are the clocks τ synchronized in? Expression (1) presents the set τ as synchronized; it is rather a plain statement that the time needed for light to travel from 0 to x' is exactly two times shorter than the entire time of the return journey, and that should stand for some ‘internal’ synchronization. At the same time, (2) treats τ as a function τ = f(x', t) of the variables belonging to the conditionally stationary frame of reference, which, if handled properly, should end in the Lorentz transforms and a set of asynchronous clocks. Thus, the clocks τ of (2) are a different set, namely the clocks as observed from not the proper frame of reference; i. e. (2) stands for some ‘external’ synchronization – which, by the way, cannot be since obviously ∂τ/∂x' ≠ 0 (in plain language, at each moment t clocks τ located at different x' spots show different time). And yet, the synchronization test is passed even for τ = f(x', t). It means that (1) is made true in either frame of reference.
One cannot have both. We have to conclude that τ is surreptitiously used to denote two different sets, both synchronized and non-synchronized clocks, and that these two conflicting notions are synthesized in (2). As far as I understand, this non-existent mathematics should render all further derivations meaningless.
It is possible to argue that this was Einstein’s attempt to make the results of the internal synchronization of τ clocks into ones not contradicting the time τ as observed from without. However, this attempt would lead to a result incompatible with the premises of the inference. The τ clocks, as is clear from the nature of (2), do not change their x' coordinate with time (are at rest relative to the x' axis), and at the same time ∂τ/∂x' ≠ 0, while ∂τ/∂x' = 0 should be just another way to define the τ set as synchronized. The travel time of light on its path from 0 to x' is thus stated to be objectively different from that on its return path. The synchronization of τ, therefore, will not stand any test other than the one suggested by Einstein: we only need to switch the point of emission and point of reflection, to send a ray of light from x' to be reflected back at 0, and the same clocks will become asynchronous – or, if we insist they are still synchronous, we come up with different factors of the linear function τ. That makes the transformation of τ dependent on the setup of the test, and synchronization comes off for one particular arrangement and not any other. Through any other test the inhabitants of the moving frame of reference will find their clocks to be objectively asynchronous and themselves indeed moving relative to ‘ether’ – that is, I must remind you, according to the setup suggested by Einstein. I am not saying whether it is possible or not to find yourself objectively moving or objectively standing still; I am merely developing his idea of this synchronization process.
Speaking of incongruities, the substitution x′ = x – vt where x', as has been observed, is motionless relative to the τ clocks, presupposes a one-to-one relation between the moving and stationary coordinate for any point x or x' for any moment t (if x′ = x – vt, then x =x′ + vt). And that means that t in this transformation plays the role of ever universal, never local time for both the coordinate x and the coordinate x'. The substitution x′ = x – vt is ‘Galilean’, while the Lorentz transformation presupposes that time of a frame of reference is now universal, now local depending on the observer, making such substitutions illegitimate.
And the most terrible part of it is that all that effort is fruitless: Einstein does not obtain the Lorentz transforms. Einstein, as is seen from (4), gets the ratio of partial derivatives of the moving frame’s time proportional to the mean velocity of light on its enclosed path, and this lacks the square root of the Lorentz factor. The transforms of y and z, that is, the coordinates which do not take part in motion, contain the Lorentz factor derived from the supposition of the propagation of light along the axes y and z (p. 6) which makes Einstein contract dimensions perpendicular to the line of motion. The transition from these ‘Einstein transforms’ to the proper Lorentz transforms in Page 7 of the article remains uncommented and unexplained.
I will finish my ruminations by telling you that no later source makes an attempt to reproduce the original derivation from the Einstein initial paper – probably because it is impossible to reproduce a nonentity? Ever since, the Lorentz transformation is deduced from the invariance of the interval. And that problem I will try to address in my following posts.
All this, if I may remind you, is not an answer but a question: I am still wondering whether there is an expert on special relativity who will make it all clear.
To be continued.
Literature
Einstein, A. On the Electrodynamics of Moving Bodies; all page numbers are as in the text available here
Previous part
Let’s Discuss Relativity of Simultaneity
Following parts
Let’s Discuss the Lorentz Transforms – Part 2
Let’s Discuss the Lorentz Transforms – Intermission
Let’s Discuss the Lorentz Transforms – Part the Last: The Real Derivation, or The Nail in the Casket