Sergey_Kovalenko May 10 2023 at 21:59

Дешевый как автобус, удобный как такси: перспективный вид общественного транспорта для больших и средних городов. Часть3

Medium

33 min

5.2K

Algorithms*Mathematics*TransportThe future is hereUrbanism

Opinion

Ссылка на Часть1: «Предварительный анализ» (ру / eng )
Ссылка на Часть2: «Эксперименты на торе» (ру / eng )
Cсылка на «Часть3: Практически значимые решения» (ру / eng )
Cсылка на «Summary» (ру / eng )

1 Игра в дипломатию

1.1 О чем эта работа

Перед вами третья и последняя публикация в цикле статей, посвященных таким схемам движения микроавтобусов, которые позволили бы достаточно быстро, достаточно дешево, а главное безо всяких пересадок доехать от любого перекрестка до любого другого перекрестка внутри большого города. Ниже вы увидите много графиков, формул и цифр, однако, перед тем как перейти к технической части, я хотел бы обсудить с вами проблему претворения всего этого замысла в жизнь и предложить вам поучаствовать в ее решении.

1.2 Головоломка для талантливых и смелых (чудаки приветствуются: 🎶)

Я предлагаю вам приключение,
я предлагаю вам игру,
я предлагаю вам стать причастными к позитивному изменению образа жизни почти миллиарда людей на всей планете,
одному мне с этим не справится.
Для начала мне потребуется ваша помощь вот в каком деле:

Один из пионеров кибернетики и доктор медицины Росс Эшби выдвинул идею, что основная задача интеллекта — это борьба с разнообразием. Живые существа и общественные институты пытаются сузить до желаемого возможные варианты будущего, пытаются препятствовать либо компенсировать поток направленной в них информации, в частности, создают информационные барьеры (от панциря черепахи до антиспам-программ). Если вы хотите оказать влияние на что-то интеллектуальное, то вам придется преодолеть его информационное противодействие. Это правили естественно, оно — почти что математический закон и его существование в нашем мире стоит принимать как данность.

Сейчас у меня есть, пусть и модельное, но достаточно хорошее решение и следующий шаг я вижу в том, чтобы попытаться преодолеть информационный барьер. Нужно сделать так, чтобы тема беспересадочного общественного транспорта стала предметом общественной дискуссии, объектом внимания потенциально заинтересованных в его реализации групп лиц. Дальше уже можно будет говорить о создании исследовательской группы, которая займется поиском решений для реальных городов и о ее финансировании.

Если у вас есть идеи, разумные советы — высказывайте их в комментариях. Если вы готовы поучаствовать лично — напишите мне письмо со своими предложениями на мой электронный адрес: magnolia@bk.ru.

Я не смогу заплатить за вашу работу сразу, но могу дать следующее публичное обещание. В случае успеха ко мне наверняка обратятся за техническими консультациями. Я не дам ни одной, пока та ваша работа, которая имеет рыночную стоимость и была направлена на результат, не будет оплачена в пятикратном размере. Если мы потерпим неудачу, то труд каждого из нас останется неоплаченным. Риск требует награды!

Я уважаю вашу потребность в самореализации. Если вы присоединитесь к проекту, то ваше участие и ваш труд будут настолько публичными, насколько вы того пожелаете.

Теперь позвольте мне высказать свое, пусть и не очень зрелое виденье того, с чем предположительно предстоит поработать.

1.3 Игровое поле и расстановка сил (🎶)

Начнем с хорошей новости.

Объем рынка.
Оценки, которые я привожу в этой статье, показывают, что беспересадочную схему движения уже можно пытаться реализовать в городах с населением в 1 миллион человек. По всему миру в городах-миллионниках проживает порядка 1 миллиарда человек. Если ежедневные транспортные расходы их усредненного жителя оценить в 3 $, то мы имеем подходящий для внедрения рынок объемом примерно 1 000 000 000 000 (1трл) $/год — это примерно треть всего ВВП Франции за 2021 год. У меня есть скромное предположение, что капитал такой величины является достаточным стимулом для изменений в экономиках целых стран и отраслей мировой промышленности. Обсудим теперь наш маленький зоопарк интересантов.

Жители крупных городов.
Наверное, самая заинтересованная и одновременно наименее влиятельная группа. В случае внедрения автобусного такси получат несколько десятков минут личного времени в сутки, комфорт и простоту перемещения по городу, свободные дороги, меньше шума и загрязнения воздуха. Имеют коллективное политическое влияние на муниципалитеты. На саму эту группу могут влиять СМИ и действия муниципалитетов.

Муниципалитеты крупных городов.
Ключевой элемент мозаики, по всей видимости, наиболее влиятельный и наименее заинтересованный. Именно администрации городов дают доступ к исследовательским данным и принимают решения о реформе транспорта. В идеальном мире от всего этого могут получить только политические очки. В реальном надо учитывать различные лобби и неформальные договоренности, которые могут как способствовать (например, со стороны фирм-производителей микроавтобусов), так и препятствовать (владельцы прежнего общественного транспорта) внедрению технологии. Возможен и крайне позитивный сценарий, когда мэр и его команда окажутся идейными новаторами.

Фирмы-производители автомобилей и автобусов.
Здесь складывается очень интересная игровая ситуация. Если появится комфортное автобусное такси, то с одой стороны оно создаст конкуренцию автомобилю и эти фирмы неминуемо потерпят убытки, а с другой — образуется новый достаточно объемный рынок по производству и обслуживанию огромного количества микроавтобусов особого типа. Потенциально, действуй автомобильные производители как единое целое, они могли бы заблокировать внедрение автобусного такси. Однако если они так поступят, то у каждого из них будет огромный стимул сжульничать и занять новый рынок раньше остальных. Первый, кто начнет массово производить микроавтобусы для совместного такси, весь бонус от захвата нового рынка получит сам, а убытки от сокращения старого — поделит между всеми. Блокирование — неустойчивая ситуация и представители автопрома попытаются ее избежать, а я — помогу им это сделать :).

Фирмы и стартапы на рынке городских пассажироперевозок.
Тоже интересная группа. Игровая ситуация для старых игроков напоминает игровую ситуацию для фирм-производителей автомобилей, но только в этот раз она значительно благоприятней. Отличие состоит в том, что автобусное такси потенциально может переманить значительную часть тех, кто раньше водил автомобиль сам, а значит изменения дают выгоду. С другой стороны, так же как и для фирм-производителей автомобилей, если фирма-оператор пассажирских перевозок решит продолжить работать по старинке, то имеет огромный риск быть вытесненной из ее старой ниши. Огромный потенциал роста для быстрых и пластичных в организаторских решениях стартапов.

Являются теми, кто непосредственно будет использовать технологию маршрутизации автобусного таки, поэтому всячески будут пытаться перетянуть одеяло на себя, все запатентовать и сделать тайной. Влияют через лобби на муниципалитеты и через рабочие места на настроение жителей города.

Исследовательские группы и университеты.
“В основном безвредны”. Как о структуре, способной на что-то влиять и быть восприимчивой к влиянию, я думаю об университетских исследовательских группах с очень большим скепсисом. Нынешняя политика вынуждает их на публикацию количества статей, а не на достижение практического результата. В то же время я допускаю, что существуют отдельные выдающиеся коллективы и личности, с которыми стоит наладить двусторонний контакт.

1.4 Образ будущего и мои личные цели: вариант 0

То решение, которое есть сейчас, подходит только для клеточных городов и вопрос о его обобщении на города других типов требует исследований. Я предполагаю, что такие обобщения существуют и даже понимаю в каком направлении двигаться. Но все это — объемный кропотливый труд, и с моей стороны было бы глупо пытаться выполнить его в одиночку. Нужна исследовательская группа. Даже если мы говорим о внедрении уже разработанной схемы автобусного такси в реальные клеточные города, а такие существуют, то “на земле” обязательно всплывет миллион мелких нюансов и проблем, для решения которых тоже нужна исследовательская группа. Я думаю, что мне интересно будет взять на себя задачу создания и координации такой группой, а мое присутствие в ней ускорит ход исследований.

Моя позиция в том, чтобы результаты исследований были открытыми, а технология общедоступной. Мне не нужен миллиард, моя жизнь стоит дороже и в ней есть еще много загадок, которые я хотел бы успеть разгадать. Конечно, такую установку трудно вписать в современный мир капитала, где промышленное знание пытаются либо превратить в собственность, либо засекретить. Но кажется, я придумал способ, как можно решить эту проблему.

Скорее всего, главными заинтересованными субъектами в результатах исследований станут фирмы, способные производить нового типа автобусы, и фирмы, которые непосредственно будут заниматься пассажирскими перевозками. Как заставить их финансово содержать независимую исследовательскую группу без передачи прав на результаты исследований?
Моя идея состоит в том, чтобы продавать этим фирмам право посольства. Я вижу это так.

Независимая исследовательская группа имеет костяк своих постоянных сотрудников с полностью прозрачными и открытыми для всех ее участников исследовательскими задачами. Периодически, скажем раз в полгода или год, результаты исследований публикуются для остального мира. Если некоторая фирма заинтересована получении более свежей информации, а заодно и подготовке своих кадров, то она может купить у независимой исследовательской группы право посольства для всоих представителей. С этим правом фирме позволяется разместить внутри независимой исследовательской группы 3-5 своих собственных сотрудников, которые автоматически получат доступ ко всей информации внутри и смогут по желанию сами присоединиться к исследовательским проектам.

Я не самый большой специалист в теории игр, но кажется в описанной только что схеме все ключевые фирмы-интересанты предпочтут купить право посольства.

1.5 Ближайшие необходимые действия

Среди первоочередного я вижу:
a) перевод на английский;
b) рецензирование;
c) поиск какого-то минимального источника денег;
d) вопрос об англоязычных площадках, где можно опубликовать переведенные статьи.
f) адаптация текста для обычных СМИ;
g) поиск контактов с сообществом архитекторов и урбанистов.

Если у вас есть какие-то соображения по поводу любого из пунктов, обязательно делитесь.

Что касается перевода, я знаю переводчицу с хорошим знанием математики и экономики, которая достаточно долгое время живет в Великобритании и поэтому хорошо понимает особенности западной культуры. Она переводила для меня “Город без пробок”. Тогда ее работу: перевод вместе с редактурой я оплатил сам.
Теперь я нуждаюсь в меценатах.
Стоимость перевода одной статьи около 20 тыс. руб.
В качестве благодарности имя мецената (или название организации-спонсора) будет указано в английской и русской версиях статьи перед авторской подписью.

Ну что же, хватит на сегодня дипломатии, давайте перейдем технической части статьи. Эта часть не является самостоятельной и чтобы ее понять, вам понадобится познакомиться с двумя предыдущими. Если формулы отображаются не корректно, попробуйте несколько раз обновить страницу.

Практически значимые решения.

В чем собственно задача

Предположим, что внутри некоторого прямоугольного клеточного города на плоскости нужно спроектировать схему автобусного сообщения. Как это сделать наилучшим способом?

Пройдя круг, мы вернулись ровно к тому же вопросу, с которого начали Часть1, однако теперь у нас есть новые знания и благодаря им мы сможем построить для автобусов такую сеть маршрутных коридоров что:

1) остановочные пункты этих автобусов покроют весь город квадратной решеткой с ячейкой размера $d \times d$ , где $inline$ — это размер квартала;
2) от любого остановочного пункта к любому другому можно будет доехать без пересадок;
3) перемещаться по городу на автобусе в среднем будет не более чем в $(1 + \lambda)$ раз времязатратнее, чем на личном автомобиле или персональном такси;
4) среднее число пассажиров в салоне будет таково, что себестоимость поездок на нашем автобусном такси будет близка к себестоимости поездок на обычном городском автобусе.

2 Автобусное такси с сетью из простых уголковых коридоров

2.1 Сеть из верхних уголков

Пусть наш город имеет размер $L_h \times L_w$ и уже разбит решеткой $\{S_{h,w}\}$ , $1 \leq h \leq H$ , $1 \leq w \leq W$ на квадраты размера $\Delta l$ . Между любыми двумя клетками $S_{h’,w’}$ и $S_{h’’,w’’}$ решетки $\{S_{h,w}\}$ такими, что они не лежат в одной и той же строке или в одном и том же столбце, можно построить в точности два $\Gamma$ -образных кратчайших клеточных пути из $S_{h’,w’}$ в $S_{h’’,w’’}$ . Что, если продолжить эти пути вплоть до границ решетки $\{S_{h,w}\}$ ?

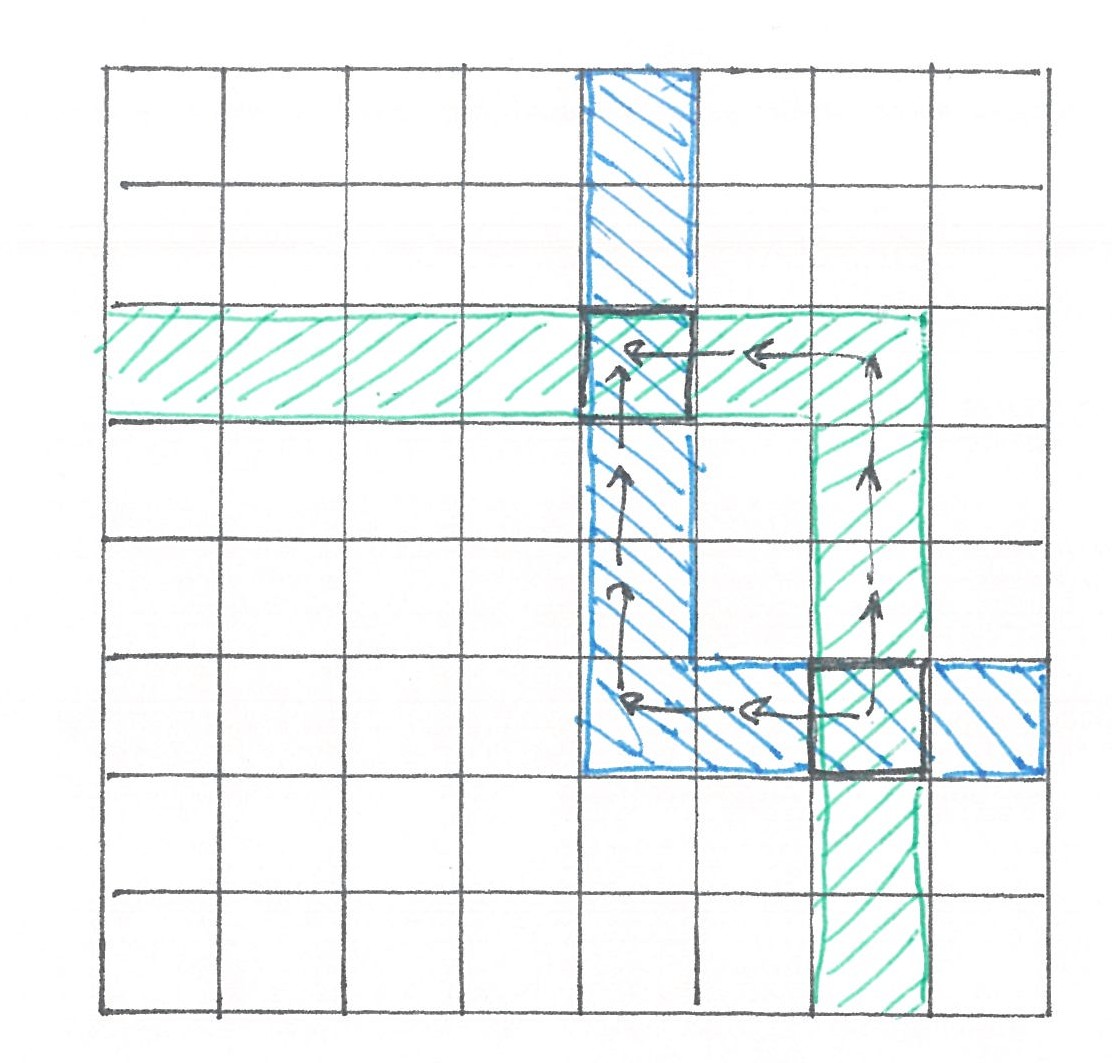
рис 1

“Уголковым” мы будем называть всякий $\Gamma$ -образный клеточный путь, который начинается и заканчивается на границе $\{S_{h,w}\}$ . Легко проверить, что каждый отрезок уголкового пути является его геодезическим отрезком. В свою очередь через любую пару клеток $S_{h’,w’}$ , $S_{h’’,w’’} in\ \{S_{h,w}\}$ проходит по крайней мере два уголковых пути: по крайней мере один из них упирается в верхнюю границу города и по крайней мере один — в нижнюю. Из этих двух фактов например следует, что множество $inline$ всех тех уголковых клеточных путей, чьи вертикальные сегменты упираются в верхний край города, и множество $inline$ всех тех уголковых клеточных путей, чьи вертикальные сегменты упираются в нижний край, оба являются геодезически связными сетями маршрутных коридоров. Индексы конкуренций у обеих этих сетей близки к 1: конкуренция в них присутствует только за перевозку пассажиров между теми парами клеток, которые находятся в одном и том же столбце или одной и той же строке.

Построим и исследуем характеристики автобусного такси с сетью $inline$ .

2.2 Число пассажиров в автобусе в зависимости от его положения внутри назначенного ему маршрутного коридора

Когда на торе мы рассматривали автобусное такси с прямоугольными маршрутами (глава 3 части 2), то имели дело с почти постоянным во времени ожидаемым числом пассажиров в салоне каждого автобуса. Для автобусного такси с сетью из уголковых маршрутов все немного иначе. Пусть $\pi$ — это коридор из $inline$ с началом в клетке $S_{y,0}$ и концом в $S_{0,x}$ (отсчет строк решетки в данном случае ведется сверху вниз). Угловой точкой для $\pi$ будет служить клетка $S_{y,x}$ . Как и в случае сети из больших прямоугольников тора, мы можем пренебречь пассажирами, чьи маршруты путешествий лежать в пределах одной стоки или одного столбца, поскольку их в целом мало и за них идет большая конкуренция. При таком рассмотрении все клиенты автобуса, следующего по маршруту $\pi$ из $S_{y,0}$ в $S_{0,x}$ сядут в него в первых $inline$ -ной клетках горизонтального участка $\pi$ и выйдут в последних $inline$ клетках вертикального

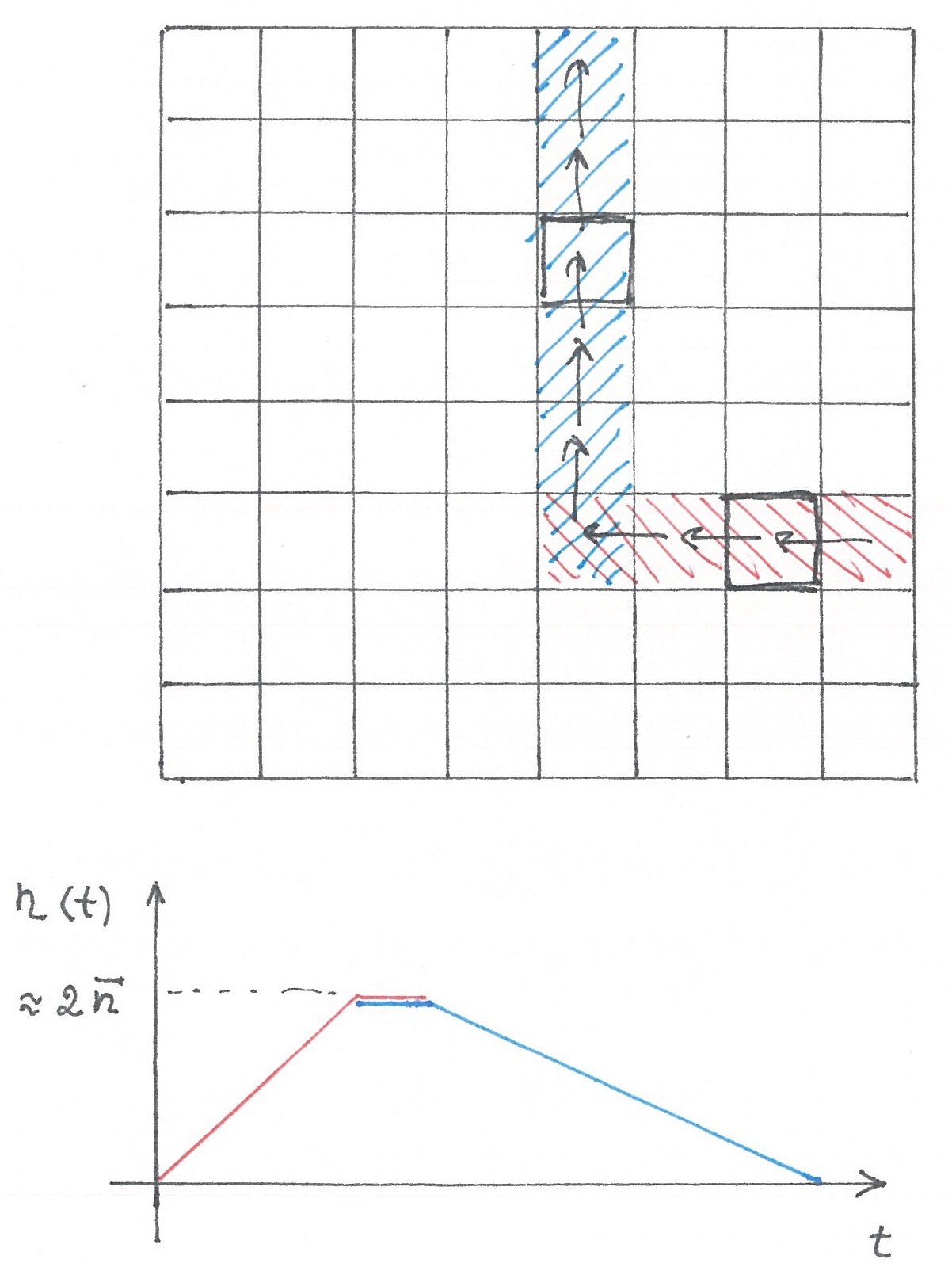
рис 2

В модели города с равномерным доступом средний поток путешествий из каждой клетки горизонтального участка в каждую клетку вертикального будет одинаковым. Одинаковость потока означает, что на горизонтальном участке $\pi$ ожидаемое число пассажиров в салоне автобуса будет линейно расти, а на вертикальном — линейно падать. Как следствие зависимость ожидаемой загрузки автобуса от времени будет описываться графиком примерно треугольной формы.

Для дальнейшего анализа нам понадобятся некоторые дополнительные обозначения. Пусть $n_{pass}(x,y)(t)$ — это ожидаемое число пассажиров в момент $inline$ внутри автобуса, приписанного уголковому коридору размера $x \times y$ . Далее $n_{pass}(x,y)$ — это значение $n_{pass}(x,y)(t)$ усредненное по большому периоду времени $inline$ , наконец $n_{pass}$ — усреднённая по всем автобусам в городе величина $n_{pass}(x,y)$ .

Максимум ожидаемое числа $n_{pass}(x,y)(t)$ пассажиров в автобусе приходится на тот момент (моменты) $inline$ , когда автобус уже собрал всех своих пассажиров на горизонтальном участке, но еще никого не высадил на вертикальном (или наоборот при поездке в обратную сторону). Другими словами, максимум $n_{pass}(x,y)(t)$ достигается, когда проходит проходит угловую зону $\pi$ :

$max_t n_{pass}(x,y)(t) = \Delta T xy \sigma (\Delta l)^4/L^2 \ \ \ \ \ (1)$

где $\sigma$ — это число новых путешественников которые появляются в области города единичной площади за единичное время.

Поскольку график $n_{pass}(x,y)(t)$ имеет треугольную форму, то его среднее по времени составляет половину от максимума, то есть:

$n_{pass}(x,y) = 1/2\ max_t n_{pass}(x,y)(t) = 1/2\ \Delta T xy \sigma (\Delta l)^4/L^2 \ \ \ \ \ (2)$

2.3 Анализ загрузки автобусов внутри отдельного уголкового коридора

Постараемся сделать так, чтобы среднее число пассажиров внутри автобуса, следующего вдоль $\pi$ было максимальным. Будем пока считать, что размер клетки $\Delta l$ уже выбран. В этом случае единственным контролируемым нами параметром является интервал между автобусами $\Delta T$ . Понятно, что чем больше $\Delta T$ , тем больше $n_{pass}(x,y)$ , однако мы возьмем $\Delta T$ слишком большим, то путешествия на автобусном такси станут слишком долгими по сравнению с путешествиями на личном автомобиле. Выразим, чему равна разница по времени между средним путешествием на автомобиле и в автобусном такси.

Среднее количество времени, которое путешественник тратит на ожидание следующего автобуса равно $\Delta T/2$ . Далее, мы будем считать, что автобус использует тот же алгоритм обхода, что и в параграфе 4.3 части 2. В таком случае каждая остановка автобуса сопряжена с боковым маневром, который удлиняет путь каждого пассажира в среднем на $\Delta l/3$ . В среднем пассажир станет участником половины всех остановок, на которых автобус подбирает и в среднем половины всех остановок, на которых автобус высаживает своих клиентов в течении одного рейса. Если мы пренебрегаем временем разгона/торможения и временем посадки/высадки, то ездка на автобусе будет дольше поездки на личном автомобиле в среднем на

$\Delta T/2 + max_t n_{pass}(x,y)(t) \cdot \Delta l/3v = \Delta T/2 + 2/3\ n_{pass}(x,y)\Delta l/v \ \ \ \ \ (3)$

Если бы поездки между клетками уголкового коридора $\pi$ путешественники совершали на личном автомобиле, то среднее время в пути составило бы:

$1/2\ (x + y) \Delta l/v \ \ \ \ \ (4)$

Потребуем чтобы в среднем дополнительные потери времени в поездке на автобусном такси не превышали $\lambda$ от среднего времени путешествия на автомобиле. Это требование устанавливает ограничение на максимальное значение $\Delta T$ :

$\Delta T/2 + 2 n_{pass}(x,y) \cdot \Delta l/3v = \lambda (x + y) \Delta l/2v \ \ \ \ \ (5)$

используя $inline$ , получаем:

$\Delta T/2 + \Delta T xy \sigma (\Delta l)^4/L^2 \cdot \Delta l/3v = \lambda (x + y) \Delta l/2v \ \ \ \ \ (6)$

откуда

$\Delta T = \lambda \frac {С_1 (x+y)}{1 + C_2xy} \ \ \ \ \ (7)$

где

$C_1 = \Delta l/v \ \ \ \ \ (8)$
$C_2 = 2/3\ \sigma (\Delta l)^5/L^2v \ \ \ \ \ (9)$

С этими сокращениями

$n_{pass}(x,y) = 1/2\ \Delta T xy \sigma (\Delta l)^4/L^2 = 3/4\ \lambda \frac {C_2xy(x+y)}{1 + C_2xy} \ \ \ \ \ (10)$

Из формулы $inline$ мы видим, что асимптотически при пропорциональном росте $inline$ и $inline$ оптимальная величина $\Delta T$ становится меньше, то есть чем длиннее и обширнее коридор, тем с меньшим интервалом по нему должны ходить автобусы.

2.4 Общее число автобусов во всем городе

Пусть как и прежде $\pi \in “Uppercorners”$ — это коридор размера $x \times y$ клеток. Число автобусов движущихся по $\pi$ в каком-либо одном из двух его направлении обозначим как $N_{bus}(x,y)$ . Если бы эти автобусы нигде не останавливались, то за один проход $\pi$ они должны были бы преодолевать расстояние величиной $\approx (x+y)\Delta l$ . Каждая остановка удлиняет путь в среднем на $\Delta l/3$ . Всего за один проход таких остановок должно быть примерно $4n_{pass}(x,y)$ , то есть эффективная длина маршрута автобуса получается равной примерно

$l_{ef}(x,y) = (x+y + 4/3\ n_{pas}(x,y))\Delta l \ \ \ \ \ (11)$

Чтобы временной интервал между автобусами в коридоре $\pi$ был равен $\Delta T$ , их число должно удовлетворять уравнению:

$N_{bus}(x,y) v \Delta T = l_{ef}(x,y) \ \ \ \ \ (12)$

откуда

$N_{bus}(x,y) = \left (\frac {(x+y)}{\Delta T} + 4/3\ \frac {n_{pas}}{\Delta T} \right ) \Delta l/v \ \ \ \ \ (13)$

или

$N_{bus}(x,y) = \frac {1 + C_2xy}{\lambda} + C_2xy= \frac {1}{\lambda} + \frac {1+\lambda}{\lambda}C_2xy \ \ \ \ \ (14)$

Ради простоты вычислений будем считать наш город квадратным: $inline$ , $inline$ . Для каждой пары допустимых x и y в сети “Uppercorners” есть в точности два (без учета направлений) коридора с горизонтальным размером $inline$ и вертикальным $inline$ . Далее, у каждого коридора $\pi \in “Uppercorners”$ имеется ровно два направления движения, откуда следует, что общее число автобусов в городе:

$N_{bus} = 4 \sum_{x=1}^N \sum_{y=1}^N N_{bus}(x,y) = 4 \sum_{x=1}^N \sum_{y=1}^N \frac {1}{\lambda} + \frac {1+\lambda}{\lambda}C_2xy \approx \frac {1}{\lambda} (4N^2 + (1 +\lambda)C_2N^4) \ \ \ \ \ (15)$

Подставляя в $inline$ $N = L/\Delta l$ и $C_2 = 2/3\ \sigma (\Delta l)^5/L^2v$ имеем:

$N_{bus} = \frac {L^2}{\lambda} \left [\frac {4}{(\Delta l)^2} + 2/3\ (1 + \lambda) \Delta l \frac {\sigma}{v} \right ] \ \ \ \ \ (16)$

Эксплуатация каждого дополнительно автобуса стоит денег и, если мы хотим сделать цену поездки как можно меньше, то должны сделать как можно меньше и число $N_{bus}$ . Дифференцируя $N_{bus}$ по единственному подконтрольному нам параметру $\Delta l$ , мы получаем условие экстремума:

$- \frac {8}{(\Delta l)^3} + 2/3\ (1 + \lambda)\frac {\sigma}{v} = 0 \ \ \ \ \ (17)$

откуда:

$\Delta l = \left (\frac {12}{1 + \lambda} \right )^{1/3} \cdot \left (\frac {\sigma}{v} \right )^{1/3} \ \ \ \ \ (18)$

и

$N_{bus} = \frac {L^2 12^{1/3} (1+\lambda)^{2/3}}{\lambda} \cdot \left ( \frac{\sigma}{v} \right )^{2/3} \ \ \ \ \ (19)$

2.5 Среднее приведенное число пассажиров в автобусе

Само по себе среднее число пассажиров в салоне в действительности не является той переменной, к которой должен стремиться бизнес. Почему? Все дело в том, что на среднюю заполняемость автобусов (машин такси) влияет не только то, насколько хорошо алгоритм находит попутчиков, но и то, насколько этот алгоритм удлиняет длину пути каждого из пассажиров. Простой пример:

Предположим, что вы нашли способ, как в персональном такси возить в среднем сразу по два клиента, но при этом увеличили путь каждого клиента в среднем в два раза. Легко сообразить, что на тот же самый город при том же самом спросе на поездки вам понадобится то же самое количесво машин такси, что и прежде. То есть в описанной только что ситуации никакой “выгоды” от совмещения поездок пассажиров вы не получили.

Хорошо, если среднее число попутчиков — это плохой показатель, к чему же тогда стоит стремиться. Очевидно, что к сокращению числа автобусов. Но как тогда сравнивать эффективность совместных поездок в разных городах? Чтобы это делать мы будем использовать “приведенное” средне число пассажиров в салоне $n_{pass}^*$ . По своему смыслу $n_{pass}^*$ показывает, как много пассажиров в среднем вез бы один автобус, если бы алгоритм подбора попутчиков вовсе не увеличивал путь ни одного из них.

При условии, что средняя скорость $\bar {v}$ движения вдоль коридоров, одинакова для всех автобусов во всем городе, обычное среднее $n_{pas}$ выражается формулой (параграф 4.2 часть 2):

$n_{pass} = \frac {P}{N_{bus} \bar {v}} \ \ \ \ \ (20)$

где P — это полная транспортная нагрузка, создаваемая городом (параграф 4.2 часть 2). В нашей модели средняя скорость $\bar {v}$ движения автобуса вдоль назначенного ему коридора лишь потому меньше максимальной разрешенной скорости v, что его маршрут из-за боковых маневров к точкам остановок оказывается длиннее оптимального. Чтобы “вычесть” влияние неоптимальности пути, мы заменим в предыдущей формуле $\bar {v}$ на $inline$ и будем считать, что

$n_{pass}^* = \frac {P}{N_{bus} v} \ \ \ \ \ (21)$

В прямоугольном городе размера $L\times L$ средняя длина поездки по кратчайшему пути равна $2/3\ L$ , соответственно транспортная нагрузка $P = 2/3\ \sigma L^3$ . Отсюда мы получаем, что для сети $inline$ среднее приведенное число пассажиров, которое везет автобус, имеет вид:

$\frac {2}{3 \cdot 12^{1/3}} \cdot \frac {\lambda L}{(1 + \lambda)^{2/3}} \cdot \left ( \frac {\sigma}{v} \right )^{1/3} \approx 0.29 \frac {\lambda L}{(1+\lambda)^{2/3}} \cdot \left ( \frac {\sigma}{v} \right )^{1/3} \ \ \ \ \ (22)$

2.6 Самый долгий интервал движения

Внутри разных маршрутных коридоров мы установили разные интервалы движения автобусов. Это было сделано из следующих соображений. Выбирая автобусное такси путешественник получает некоторый разрешенный излишек времени. В нашей модели этот излишек тратится на ожидание автобуса и неидеальность маршрута совместной поездки. Внутри малых по размеру коридоров интенсивность путешествий ниже и соответственно путь автобусов “прямее”. Отсюда следует, что при том же значении $\lambda$ мы можем заставить путешественника ждать автобус дольше, другими словами — увеличить интервал движения между автобусами и тем самым хоть немного поднять их загрузку. Раз интервал $\Delta T = \Delta T(x,y)$ является переменной величиной, давайте тогда определим, чему равно его самое большое значение.

Согласно формуле $inline$

$\Delta T = \lambda (\Delta i/v) \frac {(x+y)}{1 + C_2xy} \ \ \ \ \ (23)$

где

$C_2 = 2/3\ \sigma (\Delta l)^5/(L^2v) \ \ \ \ \ (24)$

Сделаем замену $p = x \Delta l/L$ , $q = x \Delta l/L$ , $p,q \in [0,1]$ :

$\Delta T = \lambda L/v \frac {(p+q)}{1 + pq C_2 (L/\Delta l)^2} \ \ \ \ \ (25)$

Поскольку:

$C_2 (L/\Delta l)^2 = 2/3\ \sigma (\Delta l)^3/v \ \ \ \ \ (26)$

и мы нашли, что

$- \frac {8}{(\Delta l)^3} + 2/3\ (1 + \lambda)\frac {\sigma}{v} = 0 \ \ \ \ \ (27)$

то

$C_2 (L/\Delta l)^2 = \frac {8}{1+\lambda} \ \ \ \ \ (28)$

и

$\Delta T = \lambda L/v \frac {(p+q)}{1 + \frac {8}{1+\lambda}pq} \ \ \ \ \ (29)$

В точке максимума дифференциал $\Delta T (p,q)$ должен быть равен нулю, это требование дает нам два уравнения:

$\left ( 1+ \frac {8}{1+\lambda}pq \right) - (p + q) \cdot \frac {8}{1+\lambda}p = 0 \ \ \ \ \ (30)$

$\left ( 1+ \frac {8}{1+\lambda}pq \right) - (p + q) \cdot \frac {8}{1+\lambda}q = 0 \ \ \ \ \ (31)$

откуда:

$p = q = \left ( \frac {1 + \lambda}{8} \right )^{1/2} \ \ \ \ \ (32)$

и

$\Delta T = \frac {\lambda L}{v} \cdot \left ( \frac {1 + \lambda}{8} \right )^{1/2} \ \ \ \ \ (33)$

2.7 Численные оценки для почти реальных городов

Выпишем все наши формулы вместе:

$n_{pass}^* \approx 0.29 \frac {\lambda L}{(1+\lambda)^{2/3}} \cdot \left ( \frac {\sigma}{v} \right )^{1/3} \ \ \ \ \ (34)$

$\Delta T \leq \frac {\lambda L}{v} \cdot \left ( \frac {1 + \lambda}{8} \right )^{1/2} \ \ \ \ \ (35)$

$\Delta l = \left (\frac {12}{1 + \lambda} \right )^{1/3} \cdot \left ( \frac {\sigma}{v} \right )^{1/3} \ \ \ \ \ (35)$

Возьмем наше стандартное $\lambda = 1/2$ , и посчитаем, чему были бы равны $n_{pass}^*$ , $\Delta T$ и $\Delta l$ в реальных городах, если бы те были клеточными, имели квадратную форму и реализовывали миграционную модель равномерного доступа.

$n_{pass}^*(\lambda = 1/2) \approx 0.089 L \left ( \frac{\sigma}{v} \right )^{1/3} \ \ \ \ \ (36)$
$\Delta T (\lambda = 1/2) \leq 0.22 L/v \ \ \ \ \ (37)$
$\Delta l (\lambda = 1/2) = 2 \left ( \frac {\sigma}{v} \right )^{1/3} \ \ \ \ \ (38)$

Условный квадратный Нью-Йорк (Лондон, Москва):
эффективный диаметр $L \approx 28$ км,
разрешенная скорость $inline$ км/мин
$\sigma \approx 33$ чел/мин кв км
$n_{pass}^* (\lambda = 1/2) \approx 0.089 \cdot 28 (33/0.8)^{1/3} \approx 8.6$ чел.
$\Delta l (\lambda = 1/2) \approx 2 \cdot (0.8/33)^{1/3} \approx 0.58$ км
$\Delta T (\lambda = 1/2) \leq 0.22 \cdot 28/0.8 \approx 7.7$ мин

Условный квадратный Берлин:
эффективный диаметр $L \approx 30$ км,
разрешенная скорость $inline$ км/мин
$\sigma \approx 13$ чел/мин кв км
$n_{pass}^* (\lambda = 1/2) \approx 0.089 \cdot 30 (13/0.8)^{1/3} \approx 6.8$ чел.
$\Delta l (\lambda = 1/2) \approx 2 \cdot (0.8/13)^{1/3} \approx 0.79$ км
$\Delta T (\lambda = 1/2) \leq 0.22 \cdot 30/0.8 \approx 8.3$ мин

Условный квадратный Париж:
эффективный диаметр $L \approx 10$ км,
разрешенная скорость $inline$ км/мин
$\sigma \approx 70$ чел/мин кв км
$n_{pass}^* (\lambda = 1/2) \approx 0.089 \cdot 10 (70/0.5)^{1/3} \approx 4.6$ чел.
$\Delta l (\lambda = 1/2) \approx 2 \cdot (0.5/70)^{1/3} \approx 0.39$ км
$\Delta T (\lambda = 1/2) \leq 0.22 \cdot 10/0.5 \approx 4.4$ мин

Условная квадратная Прага:
эффективный диаметр $L \approx 23$ км,
разрешенная скорость v = 0.8 км/мин
$\sigma \approx 8.3$ чел/мин кв км
$n_{pass}^* (\lambda = 1/2) \approx 0.089 \cdot 23 (8.3/0.8)^{1/3} \approx 4.5$ чел.
$\Delta l (\lambda = 1/2) \approx 2 \cdot (0.8/8.3)^{1/3} \approx 0.92$ км
$\Delta T (\lambda = 1/2) \leq 0.22 \cdot 23/0.8 \approx 6.3$ мин

Условный стандартный квадратный полумиллионный город.
население $inline$ чел,
плотность $\rho = 5000$ чел/кв км,
эффективный диаметр $inline$ км,
разрешенная скорость $inline$ км/мин
$\sigma \approx 17$ чел/мин кв км
$n_{pass}^* (\lambda = 1/2) \approx 0.089 \cdot 10 (17/1)^{1/3} \approx 2.3$ чел.
$\Delta l (\lambda = 1/2) \approx 2 \cdot (1/17)^{1/3} \approx 0.78$ км
$\Delta T (\lambda = 1/2) \leq 0.22 \cdot 10/1 \approx 2.2$ мин.

Упражнение: покритикуйте только что представленное решение сами.

3 Автобусное такси с сетью из уголковых коридоров адаптивной ширины

3.1 Еще одна возможность для улучшения

Сейчас мы модифицируем сеть $inline$ так, что эффективная загрузка курсирующих вдоль автобусов станет распределена чуть более однородно, а ее среднее значение немного возрастет.

Пусть автобус курсирует по уголковому коридору $\pi$ размера $x \ times y$ .
Величина эффективной загрузки этого автобуса пропорциональна произведению площадей вертикального и горизонтального сегментов $\pi$ и выражается формулой

$n_{pass} \approx xyA$ , где $A = 1/2 \Delta T \sigma (\Delta l)^4/L^2 \ \ \ \ \ (1)$

Эта формула показывает, что если интервал движения $\Delta T$ во всех коридорах сделать одинаковым, то чем меньше у уголкового коридора размеры $inline$ и $inline$ , тем меньшую загрузку будут иметь курсирующие по нему автобусы. В прошлой главе, чтобы хоть как-то компенсировать уменьшение величины загрузки автобусов при уменьшении $inline$ и $inline$ , мы разрешили интервалу движения $\Delta T$ быть неодинаковым в разных коридорах. Почему бы нам не пойти дальше и не позволить быть различными в разных коридорах ширине их вертикальных и горизонтальных сегментов. Чтобы это сделать разрешим вертикальному и горизонтальному сегменту уголкового коридора иметь в ширину не одну, а сразу несколько клеток. Такие уголковые коридоры мы будем называть “обобщенными”

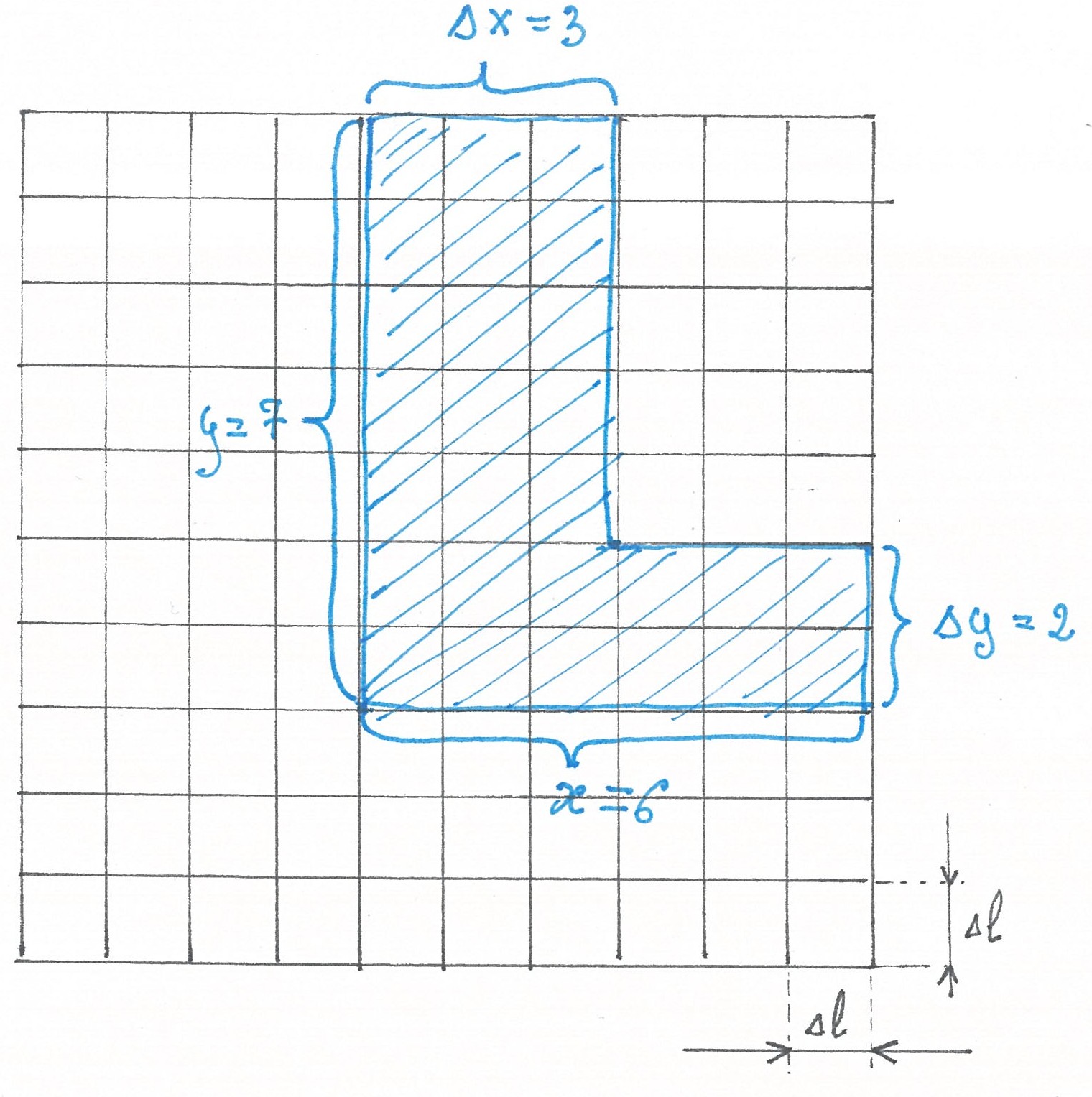
рис 3

Выраженную в клетках ширину горизонтального сегмента обобщенного коридора $\gamma$ мы будем обозначать как $\Delta y$ , а вертикального — как $\Delta x$ . Как и прежде мы будем предполагать, что через центр каждой клетки проходит горизонтальная и вертикальная уличные дороги, а посадка и высадка пассажиров осуществляется исключительно на перекрестах. Максимальная загрузка автобуса, курсирующего по $\gamma$ будет выражаться формулой:

$max_t \ n_{pass}(x,y,t) \approx A xy\Delta x\Delta y \Delta T(x,y) \ \ \ \ \ (2)$ ,

где коэффициент

$A = \sigma (\Delta l)^4/L^2 \ \ \ \ \ (3)$

не зависит от $inline$ и $inline$ .

Из $inline$ видно, что уменьшение $inline$ и $inline$ можно попытаться компенсировать увеличением $\Delta y$ и $\Delta x$ .

3.2 Анализ работы автобусного такси внутри одного обобщенного коридора

Как и в прошлой схеме, если автобус начинает свое движение с горизонтального сегмента коридора $\gamma$ , то почти все его пассажиры сядут в клетках горизонтального, а выйдут в клетках вертикального сегмента. Как и на прошлой схеме функция ожидаемого числа пассажиров в салоне автобуса $n_{pass}(x,y,t)$ от времени в пути будет иметь примерно треугольный график с максимумом в момент прохождения углового участка. В качестве следствия мы имеем:
1) среднее число пассажиров рейса подчиняется формуле

$n_{pass}(x,y) = 1/2/ max_t n_{pass}(x,y,t) =1/2\ \Delta T(x,y) xy\Delta x\Delta y \sigma (\Delta l)^4/L^2 \ \ \ \ \ (4)$

2) в среднем пассажир автобуса за одно путешествие станет участником примерно $n_{pass}(x,y)$ остановок на горизонтальном и примерно $n_{pass}(x,y)$ остановок на вертикальном участке $\gamma$ .

Каждая остановка автобуса внутри \gamma сопряжена с его предварительным боковым маневром и становится причиной дополнительного пройденный пути. Если остановка совершается на горизонтальном участке, то предварительный маневр обходится избыточным путем величиною в среднем $\Delta y \Delta l/3$ единиц длины, а если на вертикальном, то — $\Delta y \Delta l/3$ единиц длины. В итоге горизонтальный сегмент $\gamma$ автобус проедет примерно за примерно $(x\Delta l + n_{pass}(x,y)\Delta y \Delta l)/v$ единиц времени, а вертикальный — за $(y\Delta l + n_{pass}(x,y)\Delta x \Delta l)/v$ . Отсюда мы имеем, что средняя скорость продвижения автобуса вдоль горизонтального участка $\gamma$ будет равна:

$\bar {v}_{hor} \approx v \frac {x}{x + n_{pass}(x,y)\Delta y} \ \ \ \ \ (5)$

а средняя скорость вдоль горизонтального:

$\bar {v}_{ver} \approx v \frac {y}{y + n_{pass}(x,y) \Delta x} \ \ \ \ \ (6)$

По отношению к путешественникам будет честно, если средние скорости на обоих участках окажутся равными. Последнее условие это приводит нас к уравнению:

$\frac {\Delta y}{x} = \frac {\Delta x}{y} \ \ \ \ \ (7)$

Откуда в свою очередь вытекает, что:

$n_{pass}(x,y) = 1/2\ \Delta T(x,y) \frac {x^2}{y} (\Delta x)^2 \sigma (\Delta l)^4/L^2 \ \ \ \ \ (8)$

Займемся теперь подсчетом времени, которое пассажир проводит в пути. Если человек, путешествующий вдоль $\gamma$ , выбрал автобусное такси, то в среднем с учетом ожидания автобуса его поездка займет:

$\Delta T/2 + [(x + y)/2 + n_{pass}(x,y)(\Delta x + \Delta y)/3] \Delta l/v \ \ \ \ \ (9)$

единиц времени. Средняя поездка внутри $\gamma$ на личном автомобиле отняла бы в среднем:

$1/2\ (x + y)\Delta l/v \ \ \ \ \ (10)$

единиц времени. Потребуем, чтобы наше автобусное такси внутри любого \gamma в среднем было не более чем $(1 + \lambda)$ раз медленнее автомобиля. В пределе это требование приводит к уравнению:

$1/2\ \Delta T + 1/3\ n_{pass}(x,y)(\Delta x + \Delta y)\Delta l/v =1/2\ \lambda (x + y)\Delta l/v \ \ \ \ \ (11)$

Пусть $inline$ – произвольные действительные числа из отрезка $inline$ такие, что $inline$ . Положим

$1/2\ \Delta T = p [1/2\ \lambda (x + y)\Delta l/v] \ \ \ \ \ (12)$

и

$1/3\ n_{pass}(x,y)(\Delta x + \Delta y)\Delta l/v = q [1/2\ \lambda (x + y)\Delta l/v] \ \ \ \ \ (13)$

тогда:

$\Delta T = p \lambda (x + y)\Delta l/v \ \ \ \ \ (14)$

$\frac {n_{pass} (x,y)}{\Delta T}(\Delta x + \Delta y)\Delta l/3v =q/2p \ \ \ \ \ (15)$

Подставляя в $inline$ $\Delta y = (\Delta x) \ x/y$ и выражение для $n_{pass}(x,y)$ , имеем:

$\frac {x^2(x + y)}{y}(\Delta x)^3 \sigma (\Delta l)^5/L^2v = 3q/p \ \ \ \ \ (16)$

откуда:

$\Delta x = (3)^{1/3} \frac {y^{1/3}}{x^{2/3}(x + y)^{1/3}} (L)^{2/3} \left ( \frac {q}{p} \right )^{1/3} \left ( \frac {v}{\sigma} \right )^{1/3} (\Delta l)^{-5/3} \ \ \ \ \ (17)$

и

$n_{pass}(x,y) = 1/2\ \lambda p (x + y) x^2 (\Delta x)^2 \sigma (\Delta l)^5/L^2v \ \ \ \ \ (18)$

Используя $inline$ из $inline$ получаем:

$n_{pass}(x,y) = 1/2\ \lambda p \frac {y}{\Delta x} [(x + y) \frac {x^2}{y} (\Delta x)^3 \sigma (\Delta l)^5/L^2v] = 3/2\ \lambda q \frac {y}{\Delta x} \ \ \ \ \ (19)$

и окончательно:

$n_{pass}(x,y) = \frac {3^{2/3}}{2} \lambda L^{-2/3} p^{1/3}q^{2/3} x^{2/3}y^{2/3}(x + y)^{1/3} \ \ \ \ \ (20)$

3.3 Среднее приведенное число пассажиров в автобусе

Будем действовать по шаблону предыдущей главы. Проезжая в одном направлении обобщенный уголковый коридор $\gamma$ c размерами $inline$ , $inline$ , $\Delta x$ , $\Delta y$ автобус проходит эффективный путь:

$l_{ef}(x,y) \approx (x + y)\Delta l + 2n_{pass}(x,y) \left ( \frac {\Delta x \Delta l}{3} + \frac {\Delta x \Delta l}{3} \right) = (x + y)\Delta l + 2/3\ \frac {n_{pass}(x,y) \Delta x}{y}(x + y)\Delta l \ \ \ \ \ (21)$

Используя $inline$ , получаем:

$l_{ef}(x,y) \approx (1 + \lambda q)(x + y)\Delta l \ \ \ \ \ (22)$

Упражнение: получите $inline$ логически без вычислений.

Зная эффективную длину маршрута и временной интервал между автобусами, мы можем вычислить, как много таких автобусов приписано к $\gamma$

$N_{bus}(x,y) = \frac {l_{ef}(x,y)}{v \Delta T(x,y)} = \frac {1 + \lambda q}{\lambda p} \ \ \ \ \ (23)$

Чтобы найти число автобусов $N_{bus}$ во всем городе пойдем на хитрость: мысленно заменим каждый обобщенный уголковый коридор $\gamma$ на $\Delta x \Delta y$ лежащих внутри него простых уголковых клеточных путей.

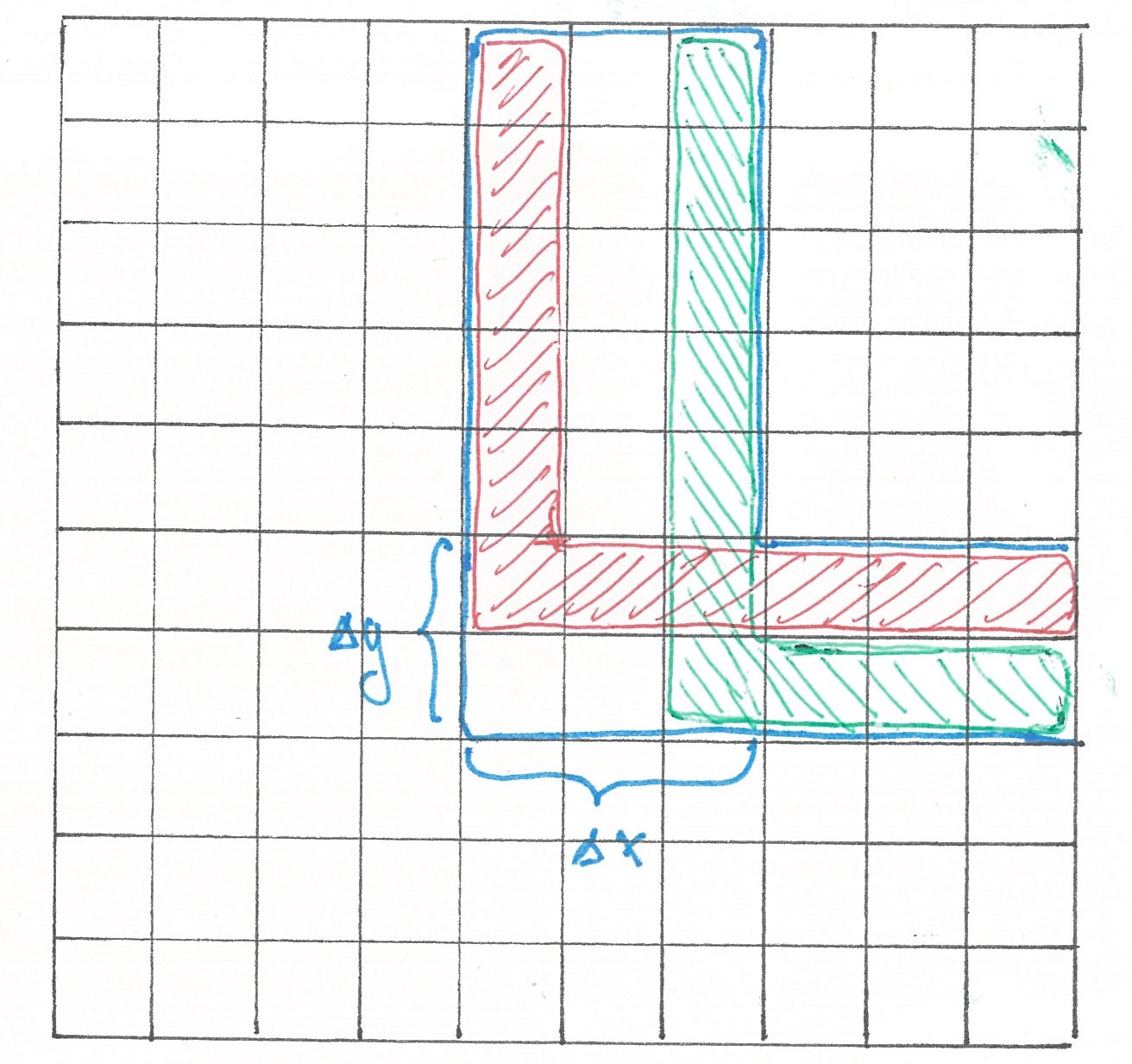
рис 4

На каждый такой путь придется

$N_{bus}^*(x,y) \approx \frac {N_{bus}(x,y)}{\Delta x \Delta y} = \frac {y N_{bus}(x,y)}{x (\Delta x)^2} \ \ \ \ \ (24)$

автобусов, из тех, что приписаны к $\gamma$ . Подставив в $inline$ выражение для $\Delta x$ и $N_{bus}(x,y)$ , получаем:

$N_{bus}^*(x,y) \approx \frac {1 + \lambda q}{\lambda p} \cdot (3)^{- 2/3} y^{1/3}x^{1/3}(x + y)^{2/3} (L)^{- 4/3} \left ( \frac {p}{q} \right )^{2/3} \left ( \frac{\sigma}{v} \right )^{2/3} (\Delta l)^{10/3} \ \ \ \ \ (25)$

или после упрощений:

$N_{bus}^*(x,y) \approx = (3)^{- 2/3} \frac {1 + \lambda q}{\lambda p^{1/3}q^{2/3}} y^{1/3}x^{1/3}(x + y)^{2/3} \left ( \frac{\sigma}{v} \right )^{2/3} (L)^{- 4/3} (\Delta l)^{10/3} \ \ \ \ \ (26)$

Полное число автобусов в городе теперь можно найти как:

$N_{bus} = 4 \sum_{x = 1}^{N} \sum_{y = 1}^{N} N_{bus}^*(x,y) \approx 4 \cdot (3)^{- 2/3} \frac {1 + \lambda q}{\lambda p^{1/3}q^{2/3}} \left ( \frac{\sigma}{v} \right )^{2/3} \int_{1}^{N} \int_{1}^{N} y^{1/3}x^{1/3}(x + y)^{2/3} (L)^{- 4/3} (\Delta l)^{10/3} dxdy \ \ \ \ \ (27)$

Чтобы в последнем выражении вычислить интеграл сделаем замену $\alpha = x \Delta l/L$ , $\beta = y \Delta l/L$ и учтем, что $N = L/\Delta l$ :

$\int_{1}^{N} \int_{1}^{N} y^{1/3}x^{1/3}(x + y)^{2/3} (L)^{- 4/3} (\Delta l)^{10/3} dxdy \approx L^2 \int_{0}^{1} \int_{0}^{1} \alpha ^{1/3} \beta^{1/3}(\alpha + \beta)^{2/3} d\alpha d\beta \ \ \ \ \ (28)$

Онлайн калькулятор двойных интегралов дает ответ $\approx 0.61$ . Если сильно не оптимизировать и взять $inline$ и $inline$ , то

$N_{bus} \approx 2.21 \frac {1 + 2/3\ \lambda}{\lambda} L^2 \left ( \frac{\sigma}{v} \right )^{2/3} \ \ \ \ \ (29)$

Транспортная нагрузка $inline$ , которую генерирует город, как мы знаем, равна $2/3 L^3 \sigma$ , следовательно приведенная средняя загрузка автобусов

$n_{pass}^* = \frac {P}{vN_{bus}} \approx 0.30 \frac {\lambda L}{1 + \lambda/2} \left ( \frac{\sigma}{v} \right )^{1/3} \ \ \ \ \ (30)$

3.4 Численные оценки для почти реальных городов

Снова возьмем $\lambda = 1/2$ , тогда

$n_{pass}^*(\lambda = 1/2) \approx 0.11 L \left ( \frac{\sigma}{v} \right )^{1/3} \ \ \ \ \ (31)$

Максимальный интервал между автобусами будет внутри двух самых больших коридоров с x = y = N:

$max_{x,y}\Delta T (\lambda = 1/2) = L/3v \ \ \ \ \ (32)$

Ширина горизонтальных и вертикальных сегментов обобщенных коридоров зависит от $inline$ , $inline$ и вообще не зависит от $\lambda$ . Чтобы составить о ней представление, вычислим ее при значениях $x \Delta l = y \Delta l = L/2$ , тогда

$\Delta r^*= (\Delta x \Delta l) = (\Delta y \Delta l) = (3)^{1/3} \frac {1}{(x\Delta l/L)^{1/3}((x +y)\Delta l/L)^{1/3}} \left ( \frac {2/3}{1/3} \right )^{1/3} \left ( \frac {v}{\sigma} \right )^{1/3} \approx 2.3 \left ( \frac {v}{\sigma} \right )^{1/3} \ \ \ \ \ (33)$

Условный квадратный Нью-Йорк (Лондон, Москва):
эффективный диаметр $L \approx 28$ км,
разрешенная скорость $inline$ км/мин
$\sigma \approx 33$ чел/мин кв км
$n_{pass}^* (\lambda = 1/2) \approx 0.11 \cdot 28 (33/0.8)^{1/3} \approx 10.6$ чел ( $inline$ в пике).
$\Delta r^* \approx 2.3 \cdot (0.8/33)^{1/3} \approx 0.67$ км
$\Delta T (\lambda = 1/2) \leq 1/3\ \cdot 28/0.8 = 11.7$ мин (в среднем $\sim 6$ мин).

Условный квадратный Берлин:
эффективный диаметр $L \approx 30$ км,
разрешенная скорость $inline$ км/мин
$\sigma \approx 13$ чел/мин кв км
$n_{pass}^* (\lambda = 1/2) \approx 0.11 \cdot 30 (13/0.8)^{1/3} \approx 8.4$ чел ( $inline$ в пике).
$\Delta r^* \approx 2.3 \cdot (0.8/13)^{1/3} \approx 0.91$ км
$\Delta T (\lambda = 1/2) \leq 1/3\ \cdot 30/0.8 = 12.5$ мин (в среднем $\sim 6$ мин).

Условный квадратный Париж:
эффективный диаметр $L \approx 10$ км,
разрешенная скорость $inline$ км/мин
$\sigma \approx 70$ чел/мин кв км
$n_{pass}^* (\lambda = 1/2) \approx 0.11 \cdot 10 (70/0.5)^{1/3} \approx 5.7$ чел ( $inline$ в пике).
$\Delta r^* \approx 2.3 \cdot (0.5/70)^{1/3} \approx 0.45$ км
$\Delta T (\lambda = 1/2) \leq 1/3\ \cdot 10/0.5 = 6.7$ мин (в среднем $\sim 3.5$ мин).

Условная квадратная Прага:
эффективный диаметр $L \approx 23$ км,
разрешенная скорость $inline$ км/мин
$\sigma \approx 8.3$ чел/мин кв км
$n_{pass}^* (\lambda = 1/2) \approx 0.11 \cdot 23 (8.3/0.8)^{1/3} \approx 5.5$ чел ( $inline$ в пике).
$\Delta r^* \approx 2.3 \cdot (0.8/8.3)^{1/3} \approx 1.1$ км
$\Delta T (\lambda = 1/2) \leq 1/3\ \cdot 23/0.8 = 9.6$ мин (в среднем $\sim 5$ мин).

Условный стандартный квадратный полумиллионный город.
население $inline$ чел,
плотность $\rho = 5000$ чел/кв км,
эффективный диаметр $inline$ км,
разрешенная скорость $inline$ км/мин
$\sigma \approx 17$ чел/мин кв км
$n_{pass}^* (\lambda = 1/2) \approx 0.11 \cdot 10 (17/1)^{1/3} \approx 2.8$ чел ( $inline$ в пике).
$\Delta r^* \approx 2.3 \cdot (1/17)^{1/3} \approx 0.90$ км
$\Delta T (\lambda = 1/2) \leq 1/3\ \cdot 10/0.5 = 6.7$ мин (в среднем $\sim 3.5$ мин).

Упражнение: рассуждения этой главы неявно предполагают, что обобщенными уголковыми коридорами адаптивной ширины можно без нахлестов “накрыть” все “простые” уголковые коридоры из $inline$ . Выясните, существует ли на самом деле сеть “Adaptivecorners” уголковых коридоров адаптивной ширины такая, что:
1) зависимость $\Delta x$ и $\Delta y$ от $inline$ , $inline$ описывается формулой $inline$ и $inline$
2) каждый простой уголковый маршрут из $inline$ как область на карте лежит внутри единственного обобщенного уголкового маршрута из $inline$ .

Если вдруг сети $inline$ с указанными свойствами нет, подумайте, насколько и как нужно ослабить требования 1) и 2), чтобы получить достаточно хороший ее эквивалент?

4 Ближе к реальности

4.1 Нарушение границ применимости и необходимость уточнения модели

В плоть до этого момента во всех построенных нами моделях совместного такси мы считали, что издержки времени, связанные с неидеальностью маршрута и ожиданием подходящей машины будут много больше временных издержек разгона/торможения возле остановок и погрузки.выгрузки пассажиров на них. Оправданны ли такие предположения? На самом деле нет!

Возьмем нашу последнюю модель с сетью $inline$ проанализируем ее результат для условного Берлина. Модель предсказывает, что при $\lambda = 1/2$ среднее число пассажиров в автобусе такси будет равно примерно $inline$ . Поскольку график ожидаемого числа пассажиров внутри автобуса имеет треугольную форму, то “ $\sim 8.5$ в среднем” означает $\sim 17$ в максимуме (в угловой точки коридора). Если так, то в среднем автобус сделает $\sim 17$ остановок, чтобы подобрать пассажиров и еще $\sim 17$ , чтобы их высадить: всего $\sim 34$ остановки. Поскольку наш условный клеточный Берлин имеет форму квадрата со стороной $L \approx 30$ км, то средняя длина путешествия в нем равна $2/3\ L = 20$ км. В этом “среднем” путешествии пассажир нашего автобуса станет участником примерно половины, то есть примерно $inline$ остановок, таким образом одна остановка автобуса такси приходится на $20/17 \approx 1.2$ километра его пути. Теперь давайте вспомним (параграф 3.2 часть 1), что даже для транзитного автобуса, который едет только по прямой и никуда не сворачивает, чтобы не быть медленнее автомобиля более чем в $inline$ раз, нужно совершать остановки не чаще чем одну на $\approx 2.5$ км.

Выходит, что мы пренебрегли чуть ли не главным. Давайте скорректируем наши вычисления.

4.2 Вычисления на пальцах

По причине громоздкости мы не буду здесь проводить точных вычислений и удовлетворимся почти точными оценками. Давайте для начала попробуем получить такие оценки для нашего условного Берлина, когда нам это удастся, мы сможем обобщить их на все модельные города.

Средний путь, который путешественник должен был бы преодолеть, если бы он использовал личный автомобиль, равен $2/3\ L = 20$ км. Средняя продолжительность путешествия на автомобиле составила бы $2/3\ L/v = 20/0.8 = 25$ мин. В расчетах прошлой главы мы предполагали, что среднее путешествие на автобусном такси будет примерно в $(1 + \lambda) = (1 + 1/2)$ раза дольше среднего путешествия на личном автомобиле, следовательно $(2\lambda /3)\ L/v = 12,5$ мин пассажир автобусного такси может потратить на ожидание автобуса и преодоление избыточной длины неидеального маршрута. При средней загрузки $в n_{pass}^* = 8.5$ человек, пассажир в среднем становится участником примерно $inline$ остановок автобуса, то есть, его потери времени без учета длительности остановок и замедлнения автобуса на участках разгона/торможения составляют примерно

$T_{exra} = \frac {lambda L}{3vn_{pass}^*} \approx 0.74 \ \ \ \ \ (1)$ мин/остановку

Каждая остановка требует двух участков разгона\торможения: в окрестности поворота к остановке и в окрестности самой остановки, это приводит к задержке примерно на $inline$ секунды (параграф 3.2 часть 1). За одну остановку в автобус садится или покидает его примерно $inline$ человек, дадим ему на это щедрые $inline$ секунд (исследования показывают, что для простого городского автобуса это время составляет $\sim 4$ секунды). Получается, что не учтенные раннее потери времени составляют примерно $T_{stop} = 42$ секунды = $inline$ мин, а значит вместо $\lambda = 1/2$ фактически мы будем иметь дело с $\lambda = 1$ . Существует простой способ вернуть $\lambda$ на место.

Заметим следующее:
1) потери времени на ожидание автобуса пропорциональны интервалу их движения $\Delta T$ :
2) среднее приведенное число пассажиров внутри салона $n_{pass}^*$ тоже пропорционально $\Delta T$ ;
3) средние потери времени пассажира от каждой остановки складываются из $T_{stop}$ и времени движения автобуса вбок, которые вместе есть константа. Последнее означает, что суммарные потери времени пассажира автобусного такси от пережитых им остановок будут пропорциональны числу последних, следовательно пропорциональны $n_{pass}^*$ , следовательно пропорциональны $\Delta T$ .
4) выходит, что не только $T_{stop}$ но и $T_{exra}$ является константой (не зависит от $\Delta T$ )

Перечисленные выше утверждения показывают, что избыточное время, которое отнимает поездка на автобусном такси по сравнению с поездкой на личном автомобиле, пропорциональна интервалу движения автобусов $\Delta T$ . Чтобы сделать $\lambda$ снова равной $inline$ изменим во всех маршрутных коридорах интервал $\Delta T$ в

$\eta = \frac {T_{exra}}{T_{exra} + T_{stop}} = 0.74/1.44 = 0.51\ \ \ \ \ (2)$

раз. Приведенное число пассажиров $n_{pass}^*$ тоже домножится на $\eta$ и станет равным

$n_{pass}^{true} \approx \eta n_{pass}^* \approx 4.3 \ \ \ \ \ (3)$

пассажирам для условного Берлина. Это результат куда хуже, чем мы имели в прошлой главе, но есть один

4.3 Кролик из шляпы: участок пешего пути

Уж если мы решили приблизить модель к условиям реальности, то должны учесть, что путешествие на общественном транспорте имеет два участка пешего пути внутри кварталов (рис). Среднее время, которое путешественник тратит на их преодоление, обозначим как $T_{ped}$ . Путь до места парковки личного автомобиля и очень медленная езда внутри квартала тоже занимают время, для простоты будем считать, что оно тоже равно $T_{ped}$ .

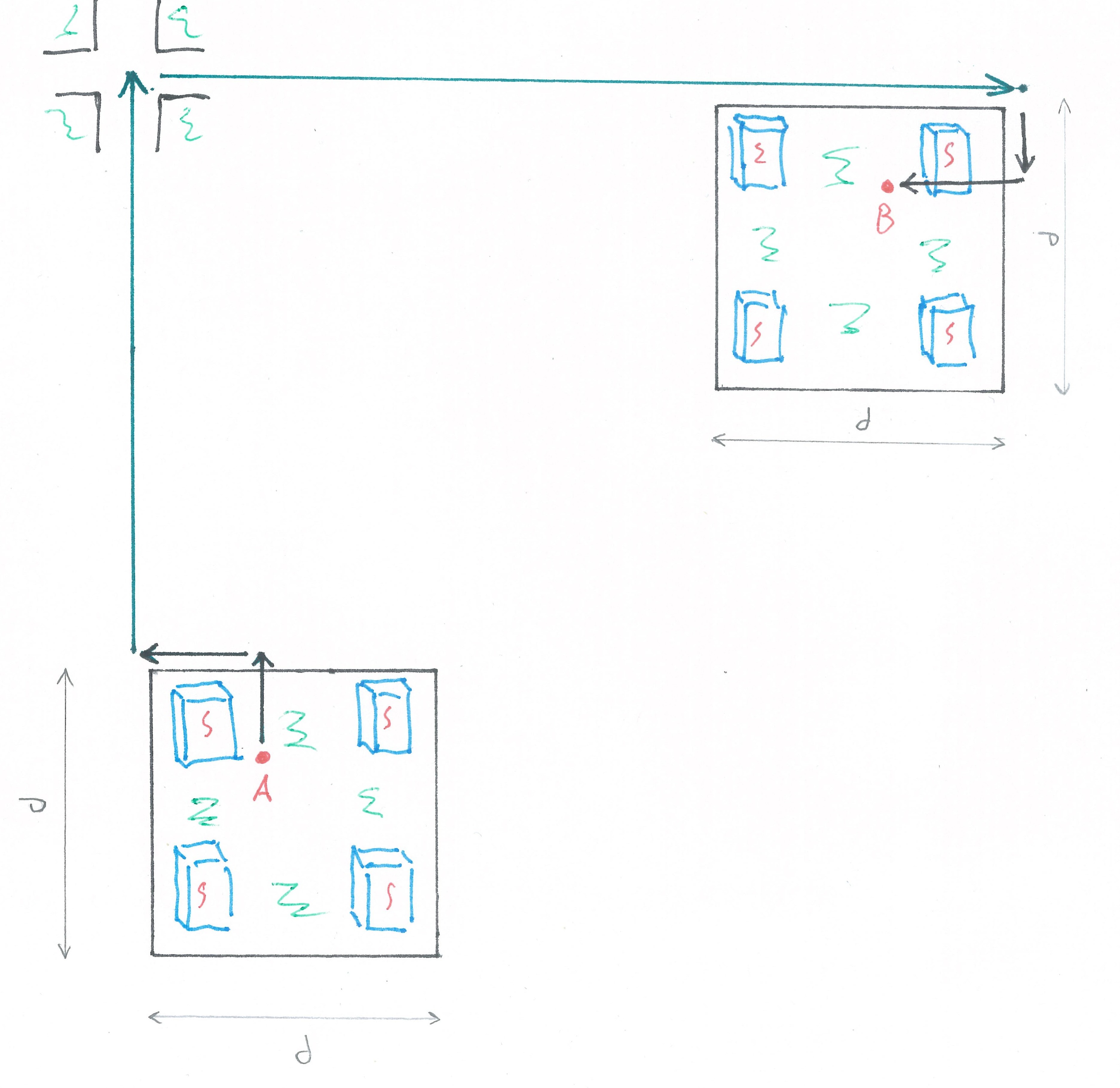
рис 5

Суммарная длина пеших путей в начале и в конце путешествия в среднем равна длине квартала. При длине квартала в $inline$ км и средней скорости пешехода в $inline$ км/ч величина $T_{ped}$ равна $inline$ часа то есть $inline$ -ти минутам.

С поправкой на пеший путь среднему путешествию на автобусном такси будет разрешено по длительности превосходить путешествие на личном автомобиле уже на время, равное

$\lambda (2/3\ L/v + T_{ped}) \ \ \ \ \ (4)$

Если $n_{pass}^{true}$ — это среднее число пассажиров в автобусе, то среднее путешествие будет сопряжено с $2 n_{pass}^{true}$ остановками, на каждой из которых путешественник потеряет в среднем $(T_{stop} + T_{extra})$ единиц времени. Эти рассуждения приводят нас к уравнению баланса:

$2 n_{pass}^{true} (T_{stop} + T_{extra}) = \lambda (2/3\ L/v + T_{ped}) = 2 n_{pass}^* T_{extra} + \lambda T_{ped} \ \ \ \ \ (5)$

откуда

$n_{pass}^{true} = n_{pass}^* \frac {T_{extra}}{T_{stop} + T_{extra}} + 1/2\ \lambda\frac {T_{ped}}{T_{stop} + T_{extra}} \ \ \ \ \ (6)$

и

$\eta = n_{pass}^{true}/ n_{pass}^* \ \ \ \ \ (7)$

Соответственно для Берлина:

$n_{pass}^{true} \approx 4.3 + 1/4\ \cdot 6/1.44 = 5.3$ чел

$\eta = 5.3/8.4 = 0.63$

Как видите, у нас появился “экстрапассажир”. Ниже приведены результаты пересчета для всех использованных нами раннее модельных городов.

Условный квадратный Нью-Йорк (Лондон, Москва):
эффективный диаметр $L \approx 28$ км,
разрешенная скорость $inline$ км/мин
$n_{pass}^*\approx 10.6$ чел.
$T_{extra} = 0.55$ мин
$n_{pass}^{true} \approx 5.9$ чел (в пике $\sim 11.8$ )
$\Delta T^{true} \leq 11.7 \cdot 5.9/10.6 = 6.5$ мин.

Условный квадратный Берлин:
эффективный диаметр $L \approx 30$ км,
разрешенная скорость $inline$ км/мин
$n_{pass}^* \approx 8.4$ чел.
$T_{extra} = 0.74$ мин
$n_{pass}^{true} \approx 5.3$ чел (в пике $\sim 10.6$ )
$\Delta T^{true} \leq 12.5 \cdot 5.3/8.4 = 7.9$ мин.

Условный квадратный Париж:
эффективный диаметр $L \approx 10$ км,
разрешенная скорость $inline$ км/мин
$n_{pass}^* \approx 5.7$ чел.
$T_{extra} = 0.58$ мин
$n_{pass}^{true} \approx 3.75$ чел (в пике $\sim 7.5$ )
$\Delta T^{true} \leq 6.7 \cdot 3.75/5.7 = 4.0$ мин.

Условная квадратная Прага:
эффективный диаметр $L \approx 23$ км,
разрешенная скорость $inline$ км/мин
$n_{pass}^* \approx 5.5$ чел.
$T_{extra} = 0.87$ мин
$n_{pass}^{true} \approx 4.0$ чел (в пике $\sim 8$ )
$\Delta T^{true} \leq 9.6 \cdot 4/5.5 = 7.0$ мин

Условный стандартный квадратный полумиллионный город.
население $inline$ чел,
плотность $\rho = 5000$ чел/кв км,
эффективный диаметр $inline$ км,
разрешенная скорость $inline$ км/мин
$\sigma \approx 17$ чел/мин кв км
$n_{pass}^* \approx 2.8$ чел.
$T_{extra} = 0.74$ мин
$n_{pass}^{true} \approx 2.5$ чел (в пике $\sim 5$ )
$\Delta T^{true} \leq 6.7 \cdot 2.5/2.8 = 6.0$ мин

Как вы видите, правдивое число пассажиров — это не золотые горы, но все же кое-что. Можно ли улучшить результат? Пусть это останется нашей с вами маленькой интригой (🎶).
.
.
.
.

5 Для тебя

Маленькому Спящему Дракону,
Юной Воспламенительнице сердец (🎶),
Мне повезло увидеть ваши чары —
Они прекрасны.
Я буду по ним скучать (🎶).
.
.
.
.
Сергей Коваленко
magnolia@bk.ru
(Это была прекрасная)
весна 2023 года.

Ссылка на Часть1: «Предварительный анализ» (ру / eng )
Ссылка на Часть2: «Эксперименты на торе» (ру / eng )
Cсылка на «Часть3: Практически значимые решения» (ру / eng )
Cсылка на «Summary» (ру / eng )

Tags:

Hubs: