Пролог
В программировании часто возникает задача найти угол между векторами. Например пишите вы прошивку для PTZ камеры. У вас есть датчик текущего положения объектива. И есть желаемое направление положения объектива. Вам надо вычислить ошибку в градусах. Вам надо определить знак ошибки и решить в какую сторону надо поворачивать чтобы затратить минимальную энергию и время.
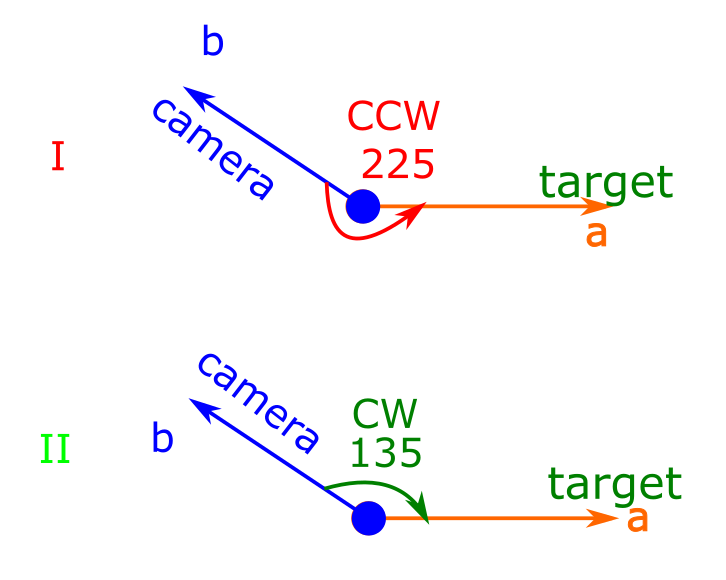
Чисто формально, между двумя векторами можно увидеть два угла: тот, что отсчитывается по часовой стрелке, и тот, что отсчитывается против часовой стрелки. В данном примере логично поворачивать камеру по часовой стрелке.
Теперь вместо PTZ камеры ставим радарную антенну и приходим к выводу, что надо решать ту же самую задачу: найти угол между векторами.
Потом в SDR обработке в цифровых PLL надо находить разность фаз между двумя комплексными числами (по сути- векторами).
Мне так часто приходилось решать задачу поиска угла между векторами, что я решил написать про это заметку.
Определения
Скаляр - число, которое не зависит от выбора системы координат. Скаляр всегда описывается одним числом
Вектор - это математический объект, который имеет величину и направление. Говоря по простому, вектор - это направленный отрезок. Пример вектора это стрелка компаса, или направление ветра в данной местности. Комплексное число a+j*b тоже можно рассматривать как вектор на плоскости.
Скалярное произведение векторов - это операция над двумя векторами, результатом которой является скаляр. Если угол между векторами прямой, то скалярное произведение равно 0.
Определитель - это скалярная величина. Используется при вычислении векторного произведения.
Векторное произведение - вектор, перпендикулярный обоим исходным векторам, длина которого численно равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой
Постановка задачи.
Даны два вектора на плоскости Va=(xa,ya,0) и Vb=(xb,yb,0). Спрашивается найти угол между этими векторами в градусах (так привычнее). Также определить знак этого угла (+ или -). Разумеется, об углах между векторами имеет смысл говорить лишь для двух ненулевых векторов.
Очевидно, что этот угол между векторами может принимать значения от -180...0... 180 градусов. Или -pi ....pi радиан. Не больше ни меньше. К слову, угол между векторами 180 Deg и -180 Deg - это один и тот же угол.
Для начала, как обыкновенно, набросаем модульных тестов. Чтобы мы понимали, что мы делаем и для чего? Какой результат мы ожидаем и чего хотим? Всё это надо отразить в списке с модульными тестами. Только потом кидаться писать код. Это же очевидно.... Вот список этих тестов.
номер | Вектор A | Вектор B | ожидаемый угол | ||
теста | a_x | a_y | b_x | b_y | градусы |
1 | 1 | 0 | 0 | 1 | +90 |
2 | 0 | 1 | 1 | 0 | -90 |
3 | 0 | 0 | 0 | 0 | Угол не определён. Может быть любой угол. |
4 | 1 | 1 | 1 | 1 | 0 |
5 | 1 | 0 | -1 | 0 | 180 |
6 | 1 | 0 | -1 | -1 | -135 |
7 | 1 | 0 | -1 | 1 | 135 |
8 | 0 | 0 | 0 | 0 | 0 |
9 | 1 | 0 | 0 | 0 | 0 |
Решение
Для вычисления этого угла придется воспользоваться линейной алгеброй и аналитической геометрией. Классическим способом вычисления модуля угла между векторами является скалярное произведение. Об этом знает даже школьник.
Как известно угол между векторами показывает скалярное произведение. Даешь два вектора, получаешь число. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними (скалярное произведение для двух векторов с координатами (a_x; a_y) и (b_x; b_y) вычисляется по формуле (1)
Как видно скалярное произведение максимально когда cos=1 то есть угол равен нулю. Одновременно скалярное произведение 0, когда векторы ортогональные (угол 90 градусов).
Из уравнения (1) можно выразить theta
Скрытый текст
\theta= arccos ( \frac{a_xb_x+a_y b_y }{\left |\overrightarrow{a} \right | \left |\overrightarrow{b} \right |}) \qquad \qquad \qquad (2)
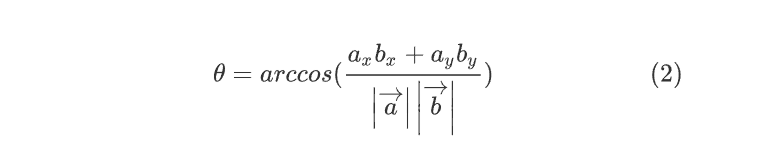
В знаменателе происходит перемножение длин векторов.
Но вот одна неприятность. Формула (2) выдает только модуль этого угла. А для всяческих систем автоматического управления, SDR обработки, нужен ещё и знак угла (+ или -) учитывая, что векторы образуют правую тройку. Да. Вот так..

Вот тут, как раз, и начитается институтская математика: матрицы, определители, векторы и прочее. Знак нам определит уже векторное произведение. Идея очень проста. Мы вычислим векторное произведение [a,b] и посмотрим на знак z компоненты получившегося результата. По сути знак угла - это знак определителя для вектора k. Это и будет знак угла между векторами.
Получается, что финальная формула для угла между векторами кристаллизируется в такой вид
Тут функция sign() - это ступенька. В положительной области определения - 1 в отрицательной области определения -1.
Громоздко? Да. Вот так... А Вы как хотели? Добро пожаловать в математику...
Программная часть
Любую математику лучше всего делать на Си. Тогда вы сможете запускать код на любой платформе. На разных микроконтроллерах, в Linux ядре, в User Spaсe и прочих программах. Си(шник) - максимально переносимый язык программирования.
typedef struct {
double dx;
double dy;
double dz;
} Vector_t;
bool is_double_equal_absolute(double d1, double d2, double precision) {
bool res = false;
qWord_t w1;
qWord_t w2;
w1.val = d1;
w2.val = d2;
if(w1.num == w2.num) {
res = true;
} else {
if(((d1 - precision) <= d2) && (d2 < (d1 + precision))) {
res = true;
} else {
res = false;
}
}
return res;
}
bool double_is_zero(double value) {
bool res = false;
res = is_double_equal_absolute(0.0, value, 0.000001);
return res;
}
double dot_product(const Vector_t*const v1, const Vector_t* const v2) {
double dot = 0.0;
dot = (v1->dx) * (v2->dx) + (v1->dy) * (v2->dy) + (v1->dz) * (v2->dz);
return dot;
}
double norm(const Vector_t* const Node) {
double norm=0.0;
if(Node) {
double argument=((Node->dx) * (Node->dx)) + ((Node->dy) * (Node->dy)) + ((Node->dz) * (Node->dz));
norm = sqrt(argument);
}
return norm;
}
double math_sign(double val) {
if (0.0 < val) {
return 1.0;
}
if (val < 0.0) {
return -1.0;
}
return 0.0;
}
/**/
double calc_angle_between_vectors_rad(
const Vector_t* const v1,
const Vector_t* const v2) {
LOG_DEBUG(MATH,"V1:%s",VectorToStr(v1));
LOG_DEBUG(MATH,"V2:%s",VectorToStr(v2));
double betta_rad = 0.0, norm1, norm2, absBetta_rad;
double dotPr;
Vector_t v3;
norm1 = norm(v1);
norm2 = norm(v2);
bool res1= double_is_zero( norm1);
bool res2= double_is_zero( norm2);
if (res1 || res2) {
return 0.0;
} else {
dotPr = dot_product(v1, v2);
absBetta_rad = acos(dotPr / (norm1 * norm2));
// scalar multiplication gives just module of the angle.
// vector multiplication gives the sign of the angle.
v3 = cross(v1, v2);
if ( double_is_zero(v3.dx) && double_is_zero(v3.dy) && double_is_zero(v3.dz)) {
betta_rad = absBetta_rad;
} else {
betta_rad = math_sign(v3.dz) * absBetta_rad;
}
}
LOG_DEBUG(MATH,"AbsTheta:%f rad,Theta:%f rad",absBetta_rad,betta_rad);
return betta_rad;
}
Как вариант можно еще вычислить угол между векторами если представить векторы как комплексные числа.
#include <complex.h>
const char* VectorToStr(const Vector_t* const Node){
static char text[80]="";
if(Node) {
strcpy(text,"");
snprintf(text,sizeof(text),"%s(dx:%f,",text,Node->dx);
snprintf(text,sizeof(text),"%sdy:%f,",text,Node->dy);
snprintf(text,sizeof(text),"%sdz:%f)",text,Node->dz);
}
return text;
}
double calc_angle_between_vectors_complex_rad(
const Vector_t* const v1,
const Vector_t* const v2) {
double arg_diff_rad = 0.0;
LOG_DEBUG(MATH,"V1:%s", VectorToStr(v1));
LOG_DEBUG(MATH,"V2:%s", VectorToStr(v2));
double complex X1= v1->dx - v1->dy * I;
double complex X2= v2->dx - v2->dy * I;
if(0.0<cabs(X1)) {
if(0.0<cabs(X2)) {
double x1_arg_rad = carg(X1);
double x2_arg_rad = carg(X2);
arg_diff_rad = x1_arg_rad-x2_arg_rad;
if (M_PI < arg_diff_rad) {
arg_diff_rad = arg_diff_rad-M_2_PI;
} else {
if(arg_diff_rad < -M_PI) {
arg_diff_rad =arg_diff_rad + M_2_PI;
}
}
}
}
LOG_DEBUG(MATH,"Theta:%f rad", arg_diff_rad);
return arg_diff_rad;
}
или так
double norm(const Vector_t* const Node) {
double norm=0.0;
if(Node) {
double argument=((Node->dx) * (Node->dx)) + ((Node->dy) * (Node->dy)) + ((Node->dz) * (Node->dz));
norm = sqrt(argument);
}
return norm;
}
double calc_angle_between_vectors_atan_rad(const Vector_t* const a,
const Vector_t* const b){
double angle_rad = 0.0;
if(a) {
if(b) {
double abs_a = norm(a);
double abs_b = norm(b);
if(abs_a) {
if(abs_b) {
LOG_DEBUG(MATH,"V1:%s",VectorToStr(a));
LOG_DEBUG(MATH,"V2:%s",VectorToStr(b));
double y=(a->dx)*(b->dy) - (a->dy)*(b->dx);
double x=(a->dx)*(b->dx) + (a->dy)*(b->dy);
angle_rad = atan2(y,x);
LOG_DEBUG(MATH,"VecAndle:%fRad ",angle_rad);
}
}
}
}
return angle_rad;
}
Отладка
Я написал консольное приложение для проверки функции вычисления угла между векторами. Как видно тесты проходят. Значит алгоритм работает.
Вот еще несколько результатов вычислений.
Функция работает.
Достоинства
++Формализм, простота и понятность. Используются широко известные и общепризнанные математические методы линейной алгебры.
++Этот код можно использовать как эталон для тестирования более простых с вычислительной точки зрения алгоритмов вычисления углов между векторами. Угол между векторами можно ещё вычислить через манипуляцию с комплексными числами или арктангенсом.
Недостатки
--Способ вычисления угла при помощи арккосинуса между векторами весьма ёмкий с вычислительной точки зрения. Тут два корня, арккосинус, умножение и сложение.
Где обычно надо вычислять угол между векторами?
1--Везде, где есть нужда хоть чем-то поворачивать. Это PTZ камеры, астрономические телескопы, лазерные дальномеры расстояний до спутников GPS, тяжелые мельницы с приводом у лопастей, ветрогенераторы, турели, строительные краны, направленные антенны (ЯГИ, параболические, АФАРы), геодезические теодолиты, солнечные батареи. Там постоянно возникает задача определения угла между векторами и наведения опорно-поворотной платформы на какую-то цель.
2--В SDR обработке на стороне приёмника (как real-time так и в post-processing(е)) есть такая вещь как фазовый детектор. Фазовый детектор- это часть ФАПЧ цепей. Фазовый детектор с программной точки зрения - это как раз определитель угла между векторами, которые образованы двумя комплексными числами виде (I+jQ): фаза от LocalOscullator (LO) и фаза сигнала с делителя частоты на выходе.
3--Подразумеваю, что вычисление углов между векторами также нужно в разработке компьютерных игр.
Итоги
Удалось научиться вычислять угол между векторами. Алгоритм вычисления угла работает.
Как видите, чтобы определить угол между векторами надо знать тригонометрию, линейную алгебру, (скалярное произведение, векторное произведение) и вычислительные методы.
Было бы здорово если бы такая операция как найти угол между векторами была реализована на аппаратном уровне прямо среди набора поддерживаемых assembler команд.
Если вам известен более простой код для вычисления угла между векторами, то пишите в комментариях.
Словарь
Акроним | Расшифровка |
PTZ | Pan Tilt Zoom |
SDR | Software-Defined Radio |
PLL | Phase-locked loop |
CCW | Counter Clock Wise |
CW | Clock Wise |
ФАПЧ | Фазовая автоподстройка частоты |
Ссылки
http://latex.codecogs.com/eqneditor/editor.php
https://rsdn.org/forum/alg/4415389.hot
Теория управления шаговым двигателем (или вертел я вашу PTZ камеру)