Если вы интересуетесь машинным обучением, то наверняка слышали про BERT и трансформеры.
BERT — это языковая модель от Google, показавшая state-of-the-art результаты с большим отрывом на целом ряде задач. BERT, и вообще трансформеры, стали совершенно новым шагом развития алгоритмов обработки естественного языка (NLP). Статью о них и «турнирную таблицу» по разным бенчмаркам можно найти на сайте Papers With Code.
С BERT есть одна проблема: её проблематично использовать в промышленных системах. BERT-base содержит 110М параметров, BERT-large — 340М. Из-за такого большого числа параметров эту модель сложно загружать на устройства с ограниченными ресурсами, например мобильные телефоны. К тому же, большое время инференса делает эту модель непригодной там, где скорость ответа критична. Поэтому поиск путей ускорения BERT является очень горячей темой.
Нам в Авито часто приходится решать задачи текстовой классификации. Это типичная задача прикладного машинного обучения, которая хорошо изучена. Но всегда есть соблазн попробовать что-то новое. Эта статья родилась из попытки применить BERT в повседневных задачах машинного обучения. В ней я покажу, как можно значительно улучшить качество существующей модели с помощью BERT, не добавляя новых данных и не усложняя модель.

Knowledge distillation как метод ускорения нейронных сетей
Существует несколько способов ускорения/облегчения нейронных сетей. Самый подробный их обзор, который я встречал, опубликован в блоге Intento на Медиуме.
Способы можно грубо разделить на три группы:
- Изменение архитектуры сети.
- Сжатие модели (quantization, pruning).
- Knowledge distillation.
Если первые два способа сравнительно известны и понятны, то третий менее распространён. Впервые идею дистилляции предложил Рич Каруана в статье “Model Compression”. Её суть проста: можно обучить легковесную модель, которая будет имитировать поведение модели-учителя или даже ансамбля моделей. В нашем случае учителем будет BERT, учеником — любая легкая модель.
Задача
Давайте разберём дистилляцию на примере бинарной классификации. Возьмём открытый датасет SST-2 из стандартного набора задач, на которых тестируют модели для NLP.
Этот датасет представляет собой набор обзоров фильмов с IMDb с разбивкой на эмоциональный окрас — позитивный или негативный. В качестве метрики на этом датасете используют accuracy.
Обучение BERT-based модели или «учителя»
Прежде всего необходимо обучить «большую» BERT-based модель, которая станет учителем. Самый простой способ это сделать — взять эмбеддинги из BERT и обучить классификатор поверх них, добавив один слой в сеть.
Благодаря библиотеке tranformers сделать это довольно легко, потому что там есть готовый класс модели BertForSequenceClassification. На мой взгляд, самое подробное и понятное руководство по обучению этой модели опубликовал Thilina Rajapakse на Towards Data Science.
Давайте представим, что мы получили обученную модель BertForSequenceClassification. В нашем случае num_labels=2, так как у нас бинарная классификация. Эту модель мы будем использовать в качестве «учителя».
Обучение «ученика»
В качестве ученика можно взять любую архитектуру: нейронную сеть, линейную модель, дерево решений. Давайте для большей наглядности попробуем обучить BiLSTM. Для начала обучим BiLSTM без BERT.
Чтобы подавать на вход нейронной сети текст, нужно представить его в виде вектора. Один из самых простых способов — это сопоставить каждому слову его индекс в словаре. Словарь будет состоять из топ-n самых популярных слов в нашем датасете плюс два служебных слова: “pad” — «слово-пустышка», чтобы все последовательности были одной длины, и “unk” — для слов за пределами словаря. Построим словарь с помощью стандартного набора инструментов из torchtext. Для простоты я не стал использовать предобученные эмбеддинги слов.
import torch
from torchtext import data
def get_vocab(X):
X_split = [t.split() for t in X]
text_field = data.Field()
text_field.build_vocab(X_split, max_size=10000)
return text_field
def pad(seq, max_len):
if len(seq) < max_len:
seq = seq + ['<pad>'] * (max_len - len(seq))
return seq[0:max_len]
def to_indexes(vocab, words):
return [vocab.stoi[w] for w in words]
def to_dataset(x, y, y_real):
torch_x = torch.tensor(x, dtype=torch.long)
torch_y = torch.tensor(y, dtype=torch.float)
torch_real_y = torch.tensor(y_real, dtype=torch.long)
return TensorDataset(torch_x, torch_y, torch_real_y)Модель BiLSTM
Код для модели будет выглядеть так:
import torch
from torch import nn
from torch.autograd import Variable
class SimpleLSTM(nn.Module):
def __init__(self, input_dim, embedding_dim, hidden_dim, output_dim, n_layers,
bidirectional, dropout, batch_size, device=None):
super(SimpleLSTM, self).__init__()
self.batch_size = batch_size
self.hidden_dim = hidden_dim
self.n_layers = n_layers
self.embedding = nn.Embedding(input_dim, embedding_dim)
self.rnn = nn.LSTM(embedding_dim,
hidden_dim,
num_layers=n_layers,
bidirectional=bidirectional,
dropout=dropout)
self.fc = nn.Linear(hidden_dim * 2, output_dim)
self.dropout = nn.Dropout(dropout)
self.device = self.init_device(device)
self.hidden = self.init_hidden()
@staticmethod
def init_device(device):
if device is None:
return torch.device('cuda')
return device
def init_hidden(self):
return (Variable(torch.zeros(2 * self.n_layers, self.batch_size, self.hidden_dim).to(self.device)),
Variable(torch.zeros(2 * self.n_layers, self.batch_size, self.hidden_dim).to(self.device)))
def forward(self, text, text_lengths=None):
self.hidden = self.init_hidden()
x = self.embedding(text)
x, self.hidden = self.rnn(x, self.hidden)
hidden, cell = self.hidden
hidden = self.dropout(torch.cat((hidden[-2, :, :], hidden[-1, :, :]), dim=1))
x = self.fc(hidden)
return xОбучение
Для этой модели размерность выходного вектора будет (batch_size, output_dim). При обучении будем использовать обычный logloss. В PyTorch есть класс BCEWithLogitsLoss, который комбинирует сигмоиду и кросс-энтропию. То, что надо.
def loss(self, output, bert_prob, real_label):
criterion = torch.nn.BCEWithLogitsLoss()
return criterion(output, real_label.float())Код для одной эпохи обучения:
def get_optimizer(model):
optimizer = torch.optim.Adam(model.parameters())
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, 2, gamma=0.9)
return optimizer, scheduler
def epoch_train_func(model, dataset, loss_func, batch_size):
train_loss = 0
train_sampler = RandomSampler(dataset)
data_loader = DataLoader(dataset, sampler=train_sampler,
batch_size=batch_size,
drop_last=True)
model.train()
optimizer, scheduler = get_optimizer(model)
for i, (text, bert_prob, real_label) in enumerate(tqdm(data_loader, desc='Train')):
text, bert_prob, real_label = to_device(text, bert_prob, real_label)
model.zero_grad()
output = model(text.t(), None).squeeze(1)
loss = loss_func(output, bert_prob, real_label)
loss.backward()
optimizer.step()
train_loss += loss.item()
scheduler.step()
return train_loss / len(data_loader)Код для проверки после эпохи:
def epoch_evaluate_func(model, eval_dataset, loss_func, batch_size):
eval_sampler = SequentialSampler(eval_dataset)
data_loader = DataLoader(eval_dataset, sampler=eval_sampler,
batch_size=batch_size,
drop_last=True)
eval_loss = 0.0
model.eval()
for i, (text, bert_prob, real_label) in enumerate(tqdm(data_loader, desc='Val')):
text, bert_prob, real_label = to_device(text, bert_prob, real_label)
output = model(text.t(), None).squeeze(1)
loss = loss_func(output, bert_prob, real_label)
eval_loss += loss.item()
return eval_loss / len(data_loader)Если это всё собрать воедино, то получится такой код для обучения модели:
import os
import torch
from torch.utils.data import (TensorDataset, random_split,
RandomSampler, DataLoader,
SequentialSampler)
from torchtext import data
from tqdm import tqdm
def device():
return torch.device("cuda" if torch.cuda.is_available() else "cpu")
def to_device(text, bert_prob, real_label):
text = text.to(device())
bert_prob = bert_prob.to(device())
real_label = real_label.to(device())
return text, bert_prob, real_label
class LSTMBaseline(object):
vocab_name = 'text_vocab.pt'
weights_name = 'simple_lstm.pt'
def __init__(self, settings):
self.settings = settings
self.criterion = torch.nn.BCEWithLogitsLoss().to(device())
def loss(self, output, bert_prob, real_label):
return self.criterion(output, real_label.float())
def model(self, text_field):
model = SimpleLSTM(
input_dim=len(text_field.vocab),
embedding_dim=64,
hidden_dim=128,
output_dim=1,
n_layers=1,
bidirectional=True,
dropout=0.5,
batch_size=self.settings['train_batch_size'])
return model
def train(self, X, y, y_real, output_dir):
max_len = self.settings['max_seq_length']
text_field = get_vocab(X)
X_split = [t.split() for t in X]
X_pad = [pad(s, max_len) for s in tqdm(X_split, desc='pad')]
X_index = [to_indexes(text_field.vocab, s) for s in tqdm(X_pad, desc='to index')]
dataset = to_dataset(X_index, y, y_real)
val_len = int(len(dataset) * 0.1)
train_dataset, val_dataset = random_split(dataset, (len(dataset) - val_len, val_len))
model = self.model(text_field)
model.to(device())
self.full_train(model, train_dataset, val_dataset, output_dir)
torch.save(text_field, os.path.join(output_dir, self.vocab_name))
def full_train(self, model, train_dataset, val_dataset, output_dir):
train_settings = self.settings
num_train_epochs = train_settings['num_train_epochs']
best_eval_loss = 100000
for epoch in range(num_train_epochs):
train_loss = epoch_train_func(model, train_dataset, self.loss, self.settings['train_batch_size'])
eval_loss = epoch_evaluate_func(model, val_dataset, self.loss, self.settings['eval_batch_size'])
if eval_loss < best_eval_loss:
best_eval_loss = eval_loss
torch.save(model.state_dict(), os.path.join(output_dir, self.weights_name))Дистилляция
Идея этого способа дистилляции взята из статьи исследователей из Университета Ватерлоо. Как я говорил выше, «ученик» должен научиться имитировать поведение «учителя». Что именно является поведением? В нашем случае это предсказания модели-учителя на обучающей выборке. Причём ключевая идея — использовать выход сети до применения функции активации. Предполагается, что так модель сможет лучше выучить внутреннее представление, чем в случае с финальными вероятностями.
В оригинальной статье предлагается в функцию потерь добавить слагаемое, которое будет отвечать за ошибку «подражания» — MSE между логитами моделей.

Для этих целей сделаем два небольших изменения: изменим количество выходов сети с 1 до 2 и поправим функцию потерь.
def loss(self, output, bert_prob, real_label):
a = 0.5
criterion_mse = torch.nn.MSELoss()
criterion_ce = torch.nn.CrossEntropyLoss()
return a*criterion_ce(output, real_label) + (1-a)*criterion_mse(output, bert_prob)Можно переиспользовать весь код, который мы написали, переопределив только модель и loss:
class LSTMDistilled(LSTMBaseline):
vocab_name = 'distil_text_vocab.pt'
weights_name = 'distil_lstm.pt'
def __init__(self, settings):
super(LSTMDistilled, self).__init__(settings)
self.criterion_mse = torch.nn.MSELoss()
self.criterion_ce = torch.nn.CrossEntropyLoss()
self.a = 0.5
def loss(self, output, bert_prob, real_label):
return self.a * self.criterion_ce(output, real_label) + (1 - self.a) * self.criterion_mse(output, bert_prob)
def model(self, text_field):
model = SimpleLSTM(
input_dim=len(text_field.vocab),
embedding_dim=64,
hidden_dim=128,
output_dim=2,
n_layers=1,
bidirectional=True,
dropout=0.5,
batch_size=self.settings['train_batch_size'])
return modelВот и всё, теперь наша модель учится «подражать».
Сравнение моделей
В оригинальной статье наилучшие результаты классификации на SST-2 получаются при a=0, когда модель учится только подражать, не учитывая реальные лейблы. Accuracy всё ещё меньше, чем у BERT, но значительно лучше обычной BiLSTM.

Я старался повторить результаты из статьи, но в моих экспериментах лучший результат получался при a=0,5.
Так выглядят графики loss и accuracy при обучении LSTM обычным способом. Судя по поведению loss, модель быстро обучилась, а где-то после шестой эпохи пошло переобучение.
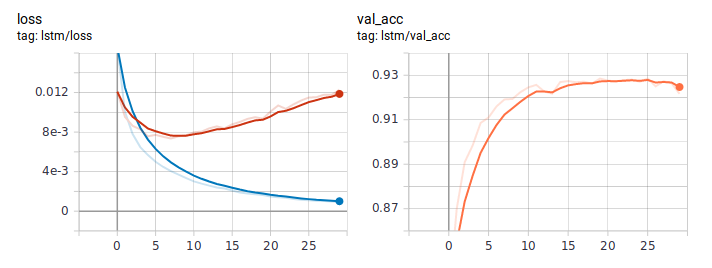
Графики при дистилляции:
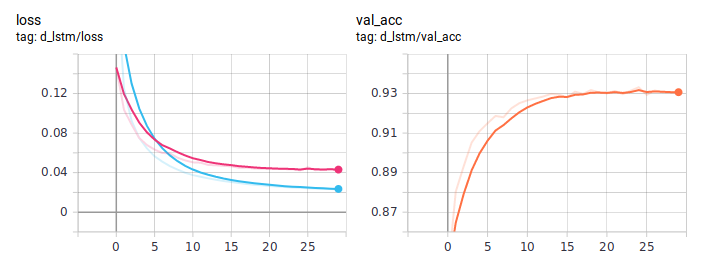
Дистиллированная BiLSTM стабильно лучше обычной. Важно, что по архитектуре они абсолютно идентичны, разница только в способе обучения. Полный код обучения я выложил на ГитХаб.
Заключение
В этом руководстве я постарался объяснить базовую идею подхода дистилляции. Конкретная архитектура ученика будет зависеть от решаемой задачи. Но в целом этот подход применим в любой практической задаче. За счёт усложнения на этапе обучения модели, можно получить значительный прирост её качества, сохранив изначальную простоту архитектуры.
