
Это 4-я статья цикла по разработке, управляемой моделями. В предыдущих статьях мы познакомились с OCL и метамоделями, Eclipse Modeling Framework и Sirius. Сегодня научимся описывать метамодели в текстовой нотации (а не в виде диаграмм как раньше) и познакомимся с табличным представлением моделей в Sirius. Сделаем это на примере кризиса среднего возраста и метода анализа иерархий. Возможно, это пригодится вам при разработке ИИ в играх, при принятии решений или в работе.
Введение
Вообще, я планировал статью про разработку DSL и преобразование моделей. Но мои планы внезапно нарушили мысли о смысле жизни, о том, тем ли я вообще занимаюсь.
Самое очевидное, что может при этом сделать специалист по разработке, управляемой моделями, это
- Выбрать метод, который позволит получить интересующие ответы (раздел 1)
- Создать метамодель под этот метод (раздел 2)
- Создать инструмент разработки моделей в соответствии с метамоделью (раздел 3)
- Создать модель (раздел 4)
- …
- Profit
Именно этим мы и займемся.
Прмечание
Если вам интересен метод анализа иерархий, но вы не хотите разбираться в метамоделях и т.п., то тут доступен Excel-калькулятор приоритетов.

1 Метод анализа иерархий
Меня интересовали следующие вопросы:
- Чем мне интересно заниматься?
- Достаточно ли времени я уделяю интересным вещам?
- Что можно изменить в жизни к лучшему?
- Не станет ли от этих изменений хуже?
- …
Когда я учился в вузе, для получения ответов на разные вопросы мы использовали метод анализа иерархий. Суть метода следующая.
- Вы определяете
- цель,
- критерии достижения цели и
- возможные альтернативы.
- Оцениваете значимость критериев.
- Оцениваете альтернативы по каждому из критериев.
- Рассчитываете приоритеты альтернатив.
- Принимаете решение.
Более подробно этот метод описан в книге Томаса Саати «Принятие решений. Метод анализа иерархий» (она легко гуглится). Кстати, в ней много примеров от психологии до мировой экономики.
1.1 Построение иерархии
Итак, в простейшем случае иерархия должна содержать цель, критерии и альтернативы.
Если суммировать все мои вопросы, то, по большому счету, меня интересует стоит ли мне сменить работу. Поэтому цель: выбрать работу.
При выборе работы меня интересует
- сколько денег я буду зарабатывать,
- на сколько интересно мне будет этим заниматься,
- будет ли у меня время на жизнь,
- карьерные перспективы,
- смогу ли я бывать на природе или буду видеть солнце и деревья раз в год,
- на сколько близка мне культура коллег, соседей и остальных людей.
При этом возможны следующие альтернативы:
- ничего не менять,
- переехать в Москву,
- переехать за границу,
- заняться фрилансом или каким-нибудь предпринимательством.
В соответствии с методом анализа иерархий строится следующая иерархия:
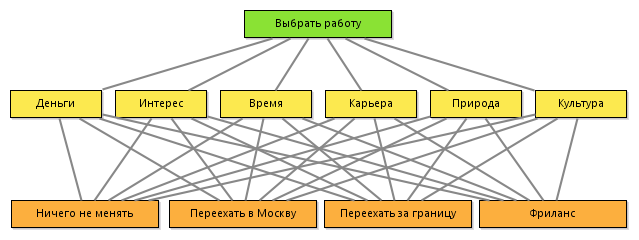
1.2 Оценка критериев
У разных людей при принятии решений могут быть примерно одинаковые критерии. Однако, их значимость может сильно различаться. Кто-то работает в большей степени ради денег, кто-то ради интереса, кому-то просто нравится общаться с коллегами и т.д.
В соответствии со своими приоритетами один человек не раздумывая выберет более денежную работу, а другой – более интересную. Не существует работы, которая по всем критериям подходит абсолютно всем.
Наверное, при принятии решений большинство людей в явной или неявной форме ранжируют критерии от самого значимого до самого незначительного. Последние отбрасывают, а по первым сравнивают возможные альтернативы. На каждую возможную работу они навешивают ярлычок: вот, эта работа более денежная, но не интересная, а эта интересная и коллектив там хороший, но сомнительные карьерные перспективы и т.д.
Если сходу не получается сделать выбор, то человек начинает переоценивать критерии: может быть интерес пока не так важен и в пробке можно лишние два часа постоять, зато там больше зарплата, вот, выплачу ипотеку и займусь чем-то интересным.
Подобные рассуждения могут продолжаться долго, мучительно и без гарантии, что в итоге действительно будет принято оптимальное решение.
В методе анализа иерархий предлагается формальный алгоритм принятия подобных решений: все критерии попарно сравниваются друг с другом по шкале от 1 до 9.
Например, что для меня важнее: интерес или деньги? Интерес важнее, но не сказать, что очень сильно. Если максимальная оценка 9 к 1, то для себя я оцениваю приоритеты как 5 к 1.
Или, например, что важнее: деньги или наличие времени для жизни, хобби? Готов ли я ради дополнительных денег работать в выходные или стоять по два часа в пробках? Я для себя оцениваю значимость этих критериев как 1 к 7.
В итоге заполняется подобная таблица:
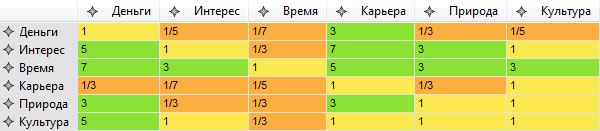
Очевидно, что по диагонали всегда будут единицы. Также очевидно, что все оценки будут обратно-симметричны относительно главной диагонали. Например, если я оцениваю значимость «интерес-деньги» как 5 к 1, то значимость «деньги-интерес» будет 1 к 5. Иногда такие матрицы называют обратно-симметричными.
В общем случае, если мы сравниваем N критериев, то необходимо сделать (N*(N-1))/2 сравнений. Казалось бы, всё только усложнилось. Если изначально было 6 критериев, то сейчас целая матрица каких-то чисел. Чтобы снова вернуться к критериям, рассчитаем собственный вектор матрицы. Элементы этого вектора и будут относительной значимостью каждого критерия.
В книге Томаса Саати предлагается несколько упрощенных методов расчета собственного вектора в уме или на бумаге. Мы воспользуемся более точным итеративным алгоритмом:
N = количество критериев
m = матрица оценок размерностью NxN
eigenvector = вектор размерностью N, заполненный значениями 1/N
Повторяем пока eigenvalue не начнет сходиться к определенному значению
или пока не сделаем максимально допустимое количество итераций
x = m * eigenvector
eigenvalue = sum(x)
eigenvector = x / eigenvalue
В итоге получаем следующий вектор:
[ 0,0592; 0,2323; 0,3846; 0,0555; 0,1220; 0,1462 ]
Наиболее значимый критерий – время (0,3846), наименее значимый – карьера (0,0555).
При парных сравнениях некоторые оценки могут получиться несогласованными. Например, для меня интерес важнее денег, а деньги важнее карьеры. Очевидно, что интерес должен быть существенно важнее карьеры. В данной таблице так и есть. Но если бы оценка для «интерес-карьера» была меньшей или вообще обратной, то мои оценки были бы не согласованы между собой.
Оценить меру этой несогласованности поможет собственное значение матрицы сравнений. Оно равно 6,7048.
Очевидно, что собственное значение пропорционально количеству критериев. Чтобы оценка согласованности не зависела от количества критериев, рассчитывается так называемый индекс согласованности = (собственное значение — N) / (N — 1).
Наконец, чтобы оценка была совсем объективной необходимо разделить данный индекс на усредненный индекс согласованности для случайных матриц. Если полученная величина (отношение согласованности) меньше 0,1000, то парные сравнения можно считать более-менее согласованными. В нашем примере оно равно 0,1137, это значит, что рассчитанным приоритетам можно более-менее доверять.
1.3 Оценка альтернатив
Теперь необходимо сравнить все альтернативы по каждому из критериев.

Например, при переезде в Москву я существенно выиграю в зарплате. Но работа, скорее всего, будет менее интересная, а также будет оставаться меньше времени для жизни. Или при переезде за границу мне придется отказаться от своего языка, подстраиваться под чужие культурные ценности.
По каждому критерию рассчитывается собственный вектор и отношение согласованности.
Полученные собственные векторы записаны в столбцах:

Отношения согласованности по каждому критерию записаны в следующем векторе:
[ 0,0337; 0,0211; 0,1012; 0,1399; 0,1270; 0,9507 ]
Большинство значений меньше или незначительно превышают 0,1000. Однако для критерия «культура» отношение согласованности получилось очень большое. Это связано с тем, что я неправильно расставил часть оценок. Хотел поставить 7 для «ничего не менять – переехать за границу», потому что жить в родном городе гораздо комфортнее. Но по ошибке поставил 1/7.
1.4 Определение приоритетов альтернатив
Итак, мы оценили критерии, навесили на каждую альтернативу ярлычок: какой вариант более денежный, какой более интересный и т.д. Теперь необходимо оценить альтернативы по всем критериям в сумме. Для этого достаточно умножить матрицу

на вектор
[ 0,0592; 0,2323; 0,3846; 0,0555; 0,1220; 0,1462 ]
В итоге мы получим следующий вектор:
[ 0,3184; 0,1227; 0,2049; 0,3540 ]
Это и есть значимости альтернатив относительно достижения цели.
1.5 Принятие решения
Теперь изобразим все рассчитанные значения на следующем рисунке:
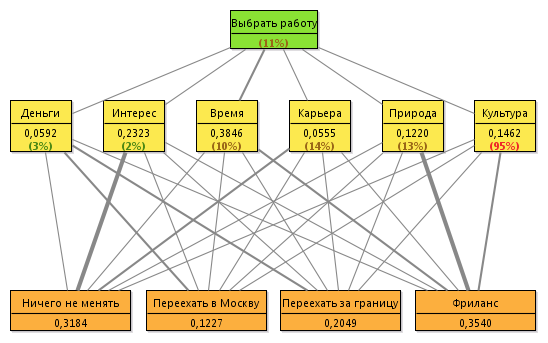
В скобках указано отношение согласованности оценок.
Толщина линий пропорциональна приоритетам. Наиболее интересна и перспективна в плане карьеры текущая работа. Фриланс позволил бы больше бывать на природе и больше времени тратить на жизнь. Более денежная работа в Москве и заграницей.
Видно, что Москва совсем отпадает. Заграница чуть лучше, но тоже не очень. Ничего не менять и фриланс примерно на одном уровне.
2 Создание метамодели
Теперь опишем как всё это рисуется и считается.
Сначала необходимо описать метамодель: виды сущностей, которые используются в методе анализа иерархий. Причем, в отличие от предыдущей статьи мы не будем рисовать метамодель в виде диаграммы, а опишем её в текстовой нотации Xcore.
Как и раньше понадобится Eclipse Modeling Tools. Установите Xcore и Sirius.
Вы можете взять либо готовый проект, либо сделать всё самостоятельно. Если самостоятельно, то создайте Xcore-проект. В папке model создайте файл ahp.xcore со следующим содержимым:
@Ecore(nsURI="http://www.example.org/ahp")
@GenModel(
modelName="AHP",
prefix="AHP",
editDirectory="/xctest.edit/src-gen",
editorDirectory="/xctest.editor/src-gen",
testsDirectory="/xctest.tests/src-gen")
package ahp
class Hierarchy
{
contains Goal[1] goal
contains Criterion[+] criteria
contains Alternative[2..*] alternatives
}
interface Named
{
String[1] name
}
class Goal extends Named { }
class Criterion extends Named { }
class Alternative extends Named { }
Смысл должен быть интуитивно понятен. Мы описали иерархию, которая содержит одну цель, хотя бы один критерий, две или более альтернативы. У всех трёх сущностей есть имя.
После сохранения файла автоматически сформируется Java API для работы с иерархиями в папке src-gen. А также будут созданы 3 дополнительных проекта. Нечто подобное мы уже делали в статье про EMF. Только там было две модели (ecore и genmodel), и генерацию кода мы запускали вручную. Xcore делает это автоматически.
Думаю, что описывать всю метамодель в статье нет смысла, вы можете посмотреть её самостоятельно.
Остановимся только на самых интересных вещах. Xcore в отличие от Ecore позволяет описывать не только структуру модели, но и некоторую логику на Java-подобном языке. Опишем, например, тип данных для хранения оценок. Положительные оценки будем хранить в виде положительных целых чисел. А обратные оценки вида 1/n будем хранить как -n. Мы могли бы хранить оценки в виде строк или в виде действительных чисел, но, наверное, это плохая идея.
При этом нам нужны две функции для преобразования оценок из или в строковое представление. На Xcore это будет выглядеть так:
type Weight wraps int
create
{
if (it.matches("\\d+")) {
Integer.parseInt(it)
}
else if (it.matches("1\\s*/\\s*\\d+")) {
val result = Integer.parseInt(it.replaceFirst("1\\s*/\\s*", ""))
if (result <= 1) 1 else -result
}
else {
throw new NumberFormatException("The weight must be either n or 1/n")
}
}
convert
{
if (it >= 1) {
it.toString
}
else if (it >= -1) {
"1"
}
else {
"1/" + (-it).toString
}
}
Xcore позволяет описывать также и относительно сложную логику.
Вот, например, операция расчета приоритетов в иерархии.
class Hierarchy
{
op void updatePriorities()
{
priorities.clear
inconsistencies.clear
val mat = new JudgmentMatrix<Criterion>(criteria)
val criteriaJudgments = judgments.filter(typeof(CriterionJudgment)).filter(cj | cj.goal == goal)
for (judgment : criteriaJudgments) {
mat.set(judgment.first, judgment.second, judgment.weight)
}
for (criterion : criteria) {
val GoalCriterionPriority priority = AHPFactory.eINSTANCE.createGoalCriterionPriority
priority.goal = goal
priority.criterion = criterion
priority.value = mat.findEigenvectorElement(criterion)
priorities.add(priority)
}
val goalInconsistency = AHPFactory.eINSTANCE.createGoalInconsistency
goalInconsistency.goal = goal
goalInconsistency.value = mat.inconsistency
inconsistencies.add(goalInconsistency)
val mat2 = new Matrix(alternatives.size, criteria.size)
criteria.forEach[criterion, j|
val mat3 = new JudgmentMatrix<Alternative>(alternatives)
val alternativeJudgments = judgments.filter(typeof(AlternativeJudgment)).filter(aj | aj.criterion == criterion)
for (judgment : alternativeJudgments) {
mat3.set(judgment.first, judgment.second, judgment.weight)
}
val criterionInconsistency = AHPFactory.eINSTANCE.createCriterionInconsistency
criterionInconsistency.criterion = criterion
criterionInconsistency.value = mat3.inconsistency
inconsistencies.add(criterionInconsistency)
alternatives.forEach[alternative, i|
val CriterionAlternativePriority priority = AHPFactory.eINSTANCE.createCriterionAlternativePriority
priority.criterion = criterion
priority.alternative = alternative
priority.value = mat3.findEigenvectorElement(alternative)
priorities.add(priority)
mat2.set(i, j, priority.value)
]
]
val mat4 = mat2.multiply(mat.eigenvector)
alternatives.forEach[alternative, i|
val GoalAlternativePriority priority = AHPFactory.eINSTANCE.createGoalAlternativePriority
priority.goal = goal
priority.alternative = alternative
priority.value = mat4.get(i)
priorities.add(priority)
]
}
}
Наконец, для Xcore-модели (как и для Ecore-модели) вы можете создать диаграмму классов.
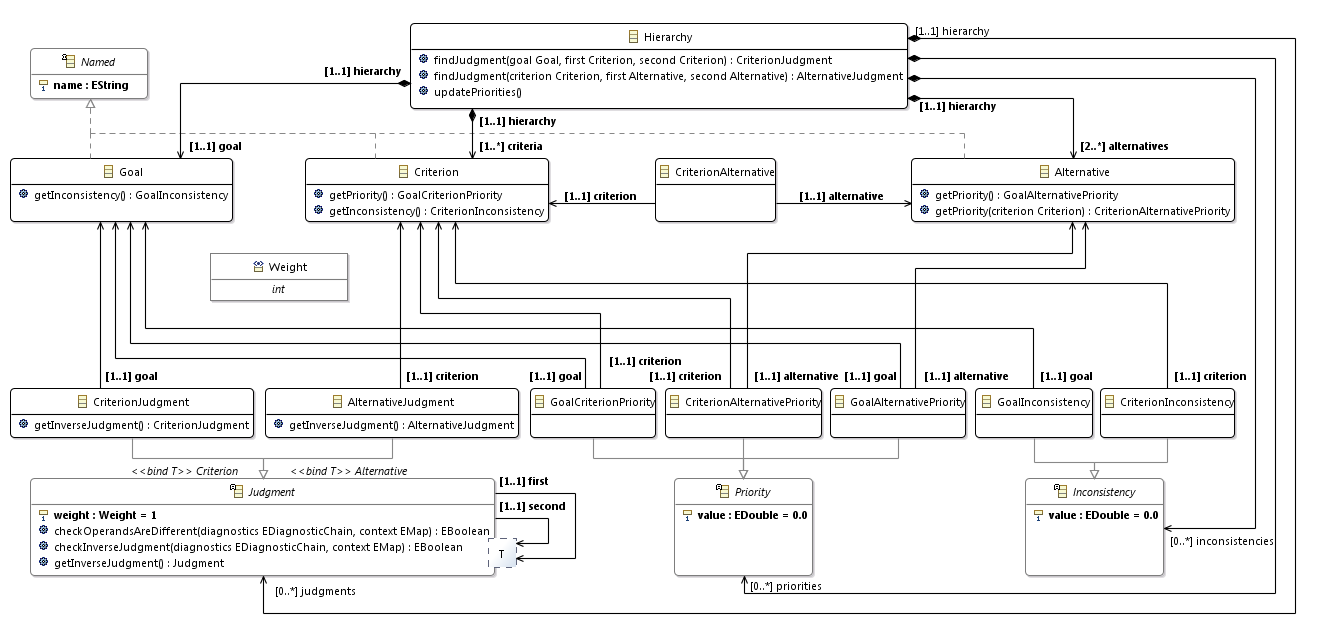
Так выглядит метамодель для метода анализа иерархий. Это максимально упрощенный вариант. А в общем случае, иерархия может содержать более трех уровней (например, у критериев могут быть подкритерии). Матрицы связей между уровнями могут быть разреженными. Оценки могут ставить несколько экспертов, а не один.
3 Разработка инструмента для работы с моделями
Метамодель готова, теперь нужен редактор иерархий и матриц. Наверное, нет смысла подробно описывать как всё это сделано. Если вам это интересно, то можете прочитать предыдущую статью про Sirius и посмотреть готовый проект.
Так выглядит спецификация редактора диаграмм и таблиц:
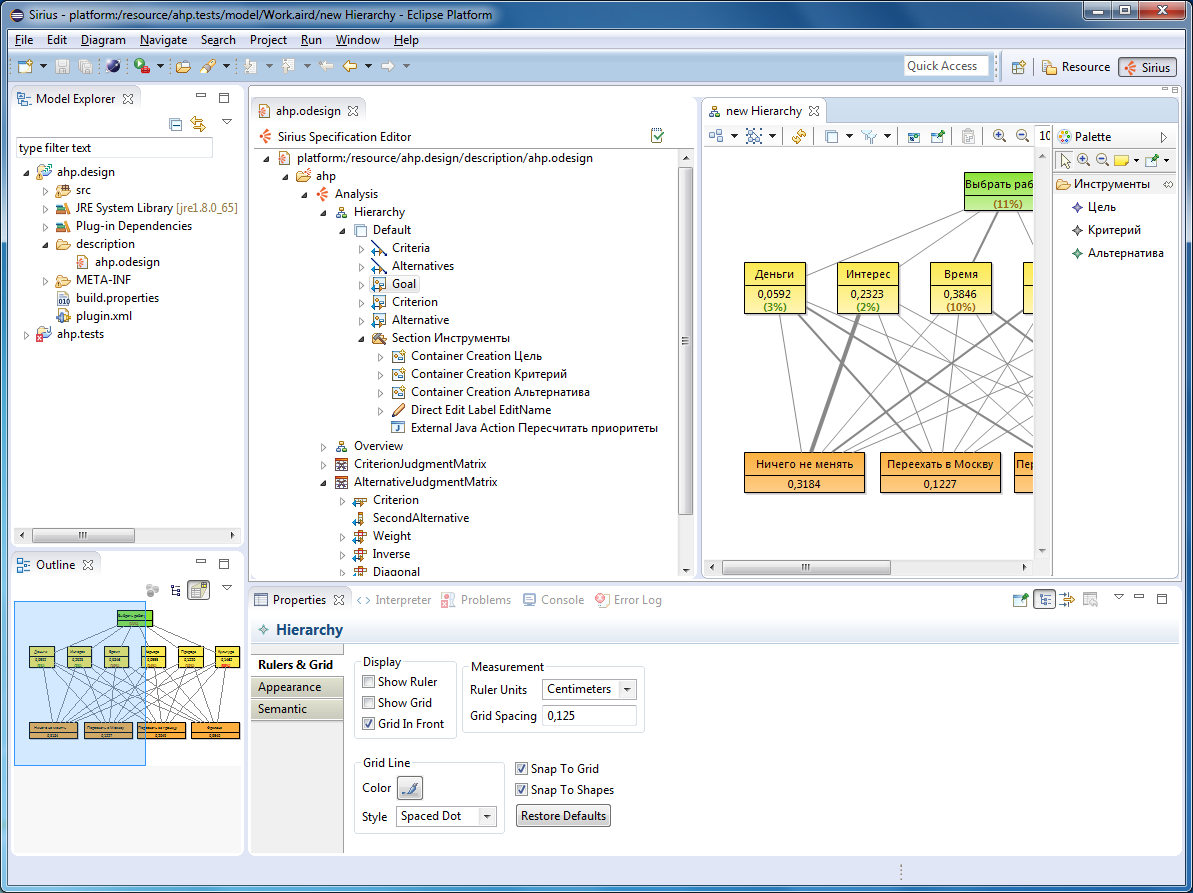
Так выглядит результирующий редактор:

Совсем декларативно описать редактор иерархий не получилось, пришлось писать расширения на Java. Думаю, стоит остановиться на этом немного подробней. В Sirius есть по крайней мере два варианта расширений: службы (service) и действия (action).
С помощью служб вы можете добавить классам из метамодели некоторые дополнительные операции. Например, следующие две операции соответственно форматируют приоритет и рассчитывают толщину связей между критериями и альтернативами.
public class Service {
public String toString(Priority priority) {
return String.format("%.4f", priority.getValue());
}
public int getEdgeWidth(Alternative alternative, EdgeTarget targetView) {
DSemanticDecorator targetNode = (DSemanticDecorator)targetView;
Criterion criterion = (Criterion)targetNode.getTarget();
Priority priority = alternative.getPriority(criterion);
return (int) (priority.getValue() * 7);
}
}
Удобно то, что эти операции вы можете использовать прямо в AQL-выражениях. Однако, вы не можете с их помощью изменять модель.
Для изменения модели нужно использовать Java-действия. Действия в отличие от служб уже не могут вызываться в AQL-выражениях. Их можно запускать, например, через контекстное меню или по нажатию кнопки. Действия можно откатывать с помощью команды Undo.
Пример действия, которое пересчитывает приоритеты в иерархии.
package ahp.design;
import java.util.Collection;
import java.util.Iterator;
import java.util.Map;
import org.eclipse.emf.ecore.EObject;
import org.eclipse.emf.transaction.RecordingCommand;
import org.eclipse.emf.transaction.TransactionalEditingDomain;
import org.eclipse.sirius.business.api.action.AbstractExternalJavaAction;
import org.eclipse.sirius.business.api.session.Session;
import org.eclipse.sirius.business.api.session.SessionManager;
import org.eclipse.sirius.diagram.DSemanticDiagram;
import ahp.Hierarchy;
public class UpdatePrioritiesAction extends AbstractExternalJavaAction {
public UpdatePrioritiesAction() {
}
@Override
public boolean canExecute(Collection<? extends EObject> arg0) {
return true;
}
@Override
public void execute(Collection<? extends EObject> selections, Map<String, Object> parameters) {
Iterator<? extends EObject> iter = selections.iterator();
if (!iter.hasNext()) {
System.out.println("Selections is empty");
return;
}
EObject obj = selections.iterator().next();
if (!(obj instanceof DSemanticDiagram)) {
System.out.println("DSemanticDiagram is expected");
}
DSemanticDiagram diagram = (DSemanticDiagram)obj;
EObject target = diagram.getTarget();
if (!(target instanceof Hierarchy)) {
System.out.println("Hierarchy is expected");
}
Hierarchy hierarchy = (Hierarchy)target;
Session session = SessionManager.INSTANCE.getSession(target);
TransactionalEditingDomain ted = session.getTransactionalEditingDomain();
RecordingCommand cmd = new RecordingCommand(ted) {
@Override
protected void doExecute() {
hierarchy.updatePriorities();
}
};
ted.getCommandStack().execute(cmd);
}
}
4 Создание модели
Ну, собственно, свою модель я уже создал и показал выше. Попробуйте взять этот проект и построить свою иерархию.
Profit
После прочтения данной статьи вы должны
- получить общее представление о методе анализа иерархий,
- научиться описывать метамодели на языке Xcore,
- научиться создавать сводные таблицы с помощью Sirius,
- научиться писать расширения для Sirius на Java.