Привет! Этот пост — немного сокращенная версия моего одноименного доклада на встрече сообщества Apache Ignite. Полную видеоверсию вместе с вопросами и ответами можно посмотреть здесь, а слайды скачать здесь. В докладе я постарался на примерах показать, как данные распределяются в Apache Ignite.
Довольно стандартная история развития любой системы требующей хранения данных и их обработки — это достижение некоторого потолка. Либо данных становится очень много и они физически не помещаются на устройство хранения, либо нагрузка растет такими темпами, что один сервер больше не в состоянии обрабатывать такое количество запросов. Нередки случаи, когда происходит и то и другое.
Как правило приходят к одному из двух решений: либо это шардирование имеющегося хранилища, либо переход на распределенную базу данных. Оба решения имеют ряд общих черт, самая очевидная из которых — это использование более чем одного узла для работы с данными. Далее множество узлов я буду называть топологией.
Проблема распределения данных по узлам топологии может быть сформулирована в виде набора требований, которым наше распределение должно удовлетворять:
Достичь выполнения первых двух требований достаточно легко.
Знакомый всем подход, часто применяемый при балансировке нагрузки между функционально эквивалентными серверами, деление по модулю N, где N — это количество узлов в топологии и мы имеем взаимно-однозначное соответствие между номером узла и его идентификатором. Тогда все что нам нужно сделать, это представить ключ объекта в виде числового значения с помощью хэш-функции и взять от полученного значения остаток от деления на N.
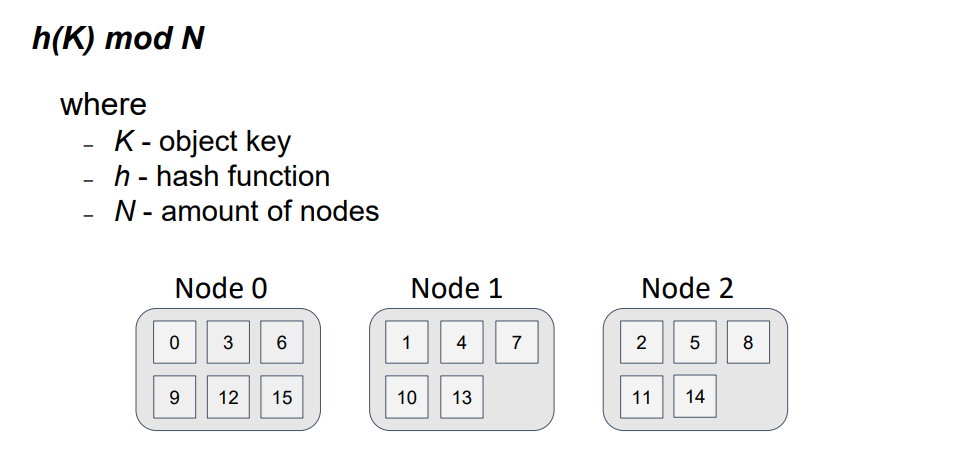
На схеме отображено распределение 16-ти ключей по 3-м узлам. Видно, что это распределение равномерно, а алгоритм получения узла для объекта прост и гарантирует, что если все узлы топологии будут использовать этот алгоритм, то для одного и того же ключа и одного и того же N будет получен один и тот же результат.
Но что будет, если мы введем в топологию 4-ый узел?
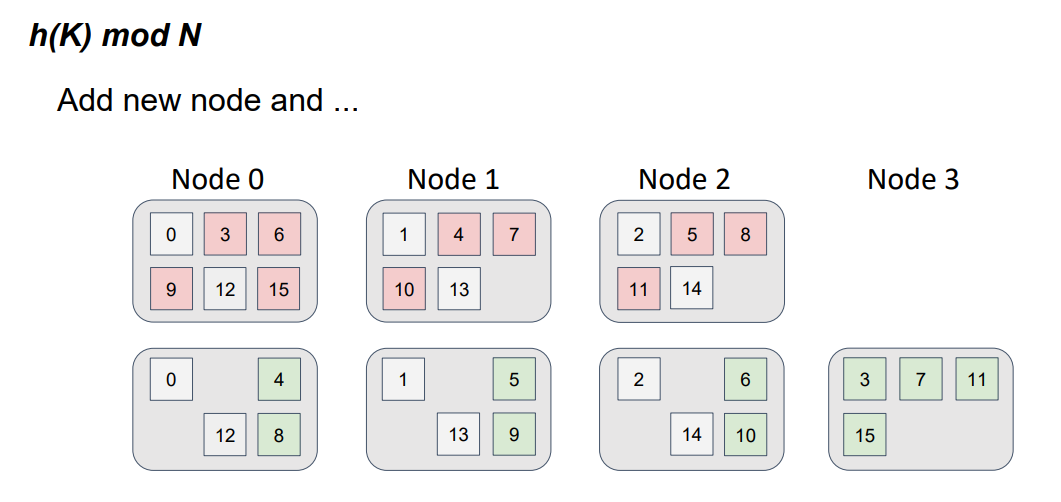
Наша функция изменилась, теперь мы берем остаток от деления на 4, а не на 3. А если изменилась функция, то изменилось и распределение, причем очень сильно.
Здесь красным цветом показано предыдущее местоположение объектов для предыдущей версии топологии из трех узлов, а зеленым соответственно положение объектов для новой версии топологии из четырех узлов. Это очень похоже на привычный многим diff файлов, только вместо файлов у нас узлы.
Легко увидеть, что данные переместились не только на новый узел, но и произошел обмен данными между узлами, которые уже были в топологии. Т.е. мы наблюдаем паразитный трафик между узлами и требование минимального изменения распределения не выполняется.
Два популярных способа решения проблемы распределения данных с учетом перечисленных требований, следующие:
Оба этих алгоритма очень просты. Их описания на Википедии укладываются в несколько предложений. Хотя их все-таки трудно назвать очевидными. Интересующимся рекомендую почитать оригинальные статьи Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web и A Name-BasedMapping Scheme for Rendezvous. Наиболее понятно, на мой взгляд, идея алгоритма консистентного хэширования донесена в этом стэндфорском курсе.
Давайте рассмотрим эти алгоритмы более подробно.
Хитрость, лежащая в основе алгоритма консистентного хэширования, состоит в том, чтобы и узлы и хранимые объекты отобразить на одно и тоже пространство идентификаторов. Это делает наши, казалось бы разные сущности, объекты и узлы, сравнимыми.
Для получения такого отображения будем просто применять одну и ту же хэш-функцию к ключам объектов и к идентификаторам узлов. Результат хэш-функции для узла будем называть токеном, это нам пригодится позже.
Представим наше пространство идентификаторов в виде окружности, т.е. просто будем считать, что за максимальным значением идентификатора сразу же следует минимальное значение идентификатора.
Теперь для того, чтобы определить на каком узле живет объект, нужно получить значение хэш-функции от его ключа, а затем просто двигаться по окружности по часовой стрелке, пока не встретим на пути токен какого-либо узла. Направление движения неважно, но оно должно быть фиксированным.
Воображаемое движение по часовой стрелке функционально эквивалентно бинарному поиску по отсортированному массиву токенов узлов.
На схеме каждый сектор отдельного цвета отражает пространство идентификаторов, за которое ответственен конкретный узел.
Если мы добавим новый узел, то…
… он разделит один из секторов на две части и полностью заберет на себя соответствующие ключи.
В данном примере узел 3 забрал на себя часть ключей узла 1.
Как видите, этот подход дает довольно неравномерное распределение объектов по узлам, т.к. он сильно зависим от идентификаторов самих узлов. Как можно улучшить этот подход?
Можно назначить узлам не один, а несколько токенов (обычно это сотни). Добиться этого можно например введением множества хэш-функций для узла (по одной на токен) или многократным последовательным применением одной и той же хэш-функции к токену, полученному на предыдущем шаге. Но нужно не забывать о коллизиях. Не должно быть двух узлов с одинаковым токеном.
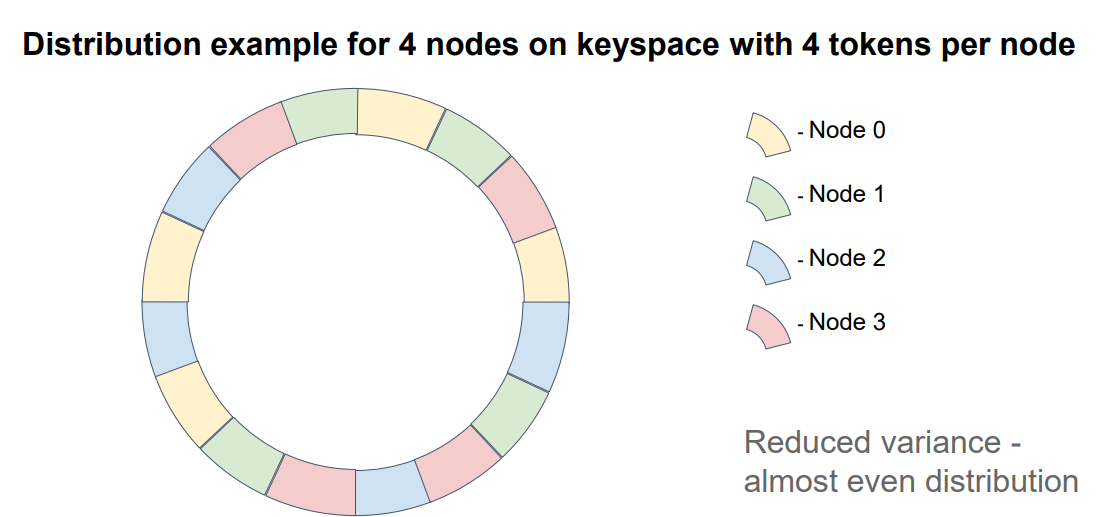
В данном примере каждый узел имеет 4 токена.
Что еще важно упомянуть: если мы хотим обеспечить сохранность данных в случае выхода какого-либо узла из топологии, то нам нужно хранить ключи на нескольких узлах (т.н. репликах или бэкапах). В случае алгоритма консистеного хэширования репликами будут следующие N-1 узлов на окружности, где N — это фактор репликации. Конечно порядок узлов должен определяться по конкретному токену (например по первому), т.к. при использовании множества токенов для каждого из них порядок расположения узлов может отличаться. Обратите внимание на схему: в ней нет четкого паттерна повторения узлов.
Что касается требования минимального изменения распределения при изменении топологии, то оно выполняется из-за того, что взаимный порядок узлов на окружности неизменен. Т.е. удаление узла из топологии не изменит отношение порядка между оставшимися узлами.
Алгоритм Rendezvous hashing кажется еще более простым, чем консистентное хэширование. В основе алгоритма лежит тот же принцип неизменности отношения порядка. Но вместо того, чтобы делать сравнимыми и узлы и объекты, мы делаем сравнимыми лишь узлы для конкретного объекта. Т.е. мы определяем отношение порядка между узлами для каждого объекта независимо.
Помогает нам в этом опять же хэширование. Но теперь, для того, чтобы определить вес узла N для данного объекта O, мы смешаем идентификатор объекта с идентификатором узла и возьмём хэш уже от этого микса. Проделав эту операцию для каждого узла мы получим набор весов, по которым и отсортируем узлы.
Узел, оказавшийся первым и будет отвечать за хранение объекта.
Так как все узлы топологии используют одни и те же входные данные, результат для них будет идентичным. Что удовлетворяет первому требованию.
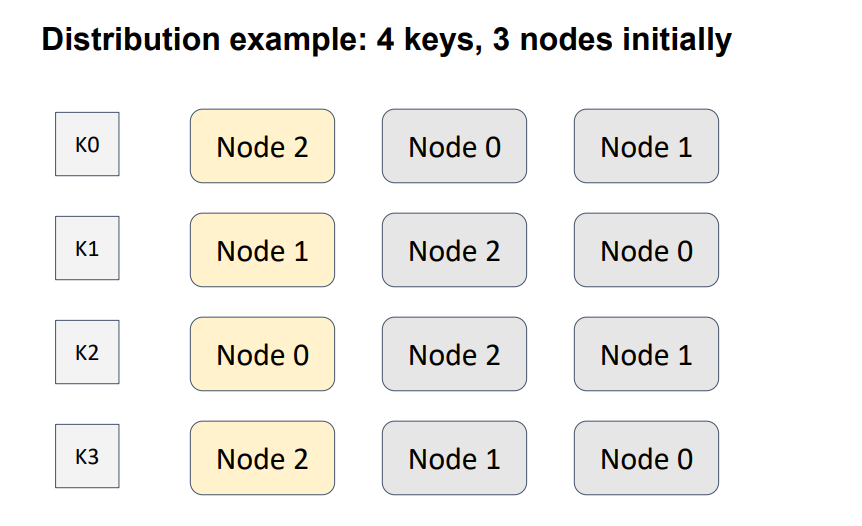
Рассмотрим пример. Здесь у нас определено отношение порядка между тремя узлами для четырех различных ключей. Желтым обозначен узел с наибольшим весом, т.е. тот узел который будет в итоге отвечать за конкретный ключ.
Добавим еще один узел в топологию.

Я намеренно поместил его в диагональ, чтобы учесть все возможные варианты. Здесь узел 3, обозначенный зеленым цветом, вошел в топологию. Следовательно, развесовка узлов для каждого из ключей изменилась. Красным цветом обозначены узлы, которые изменили свое местоположение в списке для конкретного ключа, т.к. веса этих узлов оказались меньше, чем вес добавленного узла. При этом данное изменение повлияло лишь на один из ключей, K3.
Давайте вероломно выведем узел из топологии.

Вновь изменения коснулись лишь одного ключа, на этот раз K1. Остальные объекты не пострадали. Причиной тому, как и в случае с консистентным хэшированием, является неизменность отношения порядка между любой парой узлов. Т.е. требование минимального изменения распределения выполняется и не наблюдается паразитного трафика между узлами.
Распределение для rendezvous выглядит довольно хорошо и не требует дополнительных ухищрений по сравнению с консистентным хэшированием вроде токенов.
В случае, если мы хотим поддержать репликацию, то следующий в списке узел будет первой репликой для объекта, следующий узел второй репликой и т.д.
За распределение данных в Apache Ignite отвечает так называемая аффинити-функция (см. интерфейс AffinityFunction). Реализация по-умолчанию — rendezvous hashing (см. класс RendezvousAffinityFunction).
Первое, на что нужно обратить внимание, это то, что Apache Ignite не отображает хранимые объекты напрямую на узлы топологии. Вместо этого вводится дополнительное понятие — партиция.
Партиция является контейнером для объектов и единицей репликации. Кроме того, количество партиций для конкретного кэша (это аналог таблицы в привычных нам базах данных) задается на этапе конфигурирования и не изменяется в течении жизненного цикла кэша.
Таким образом мы можем отображать объекты на партиции, используя эффективное деление по модулю, а для отображения партиций на узлы использовать rendezvous hashing.
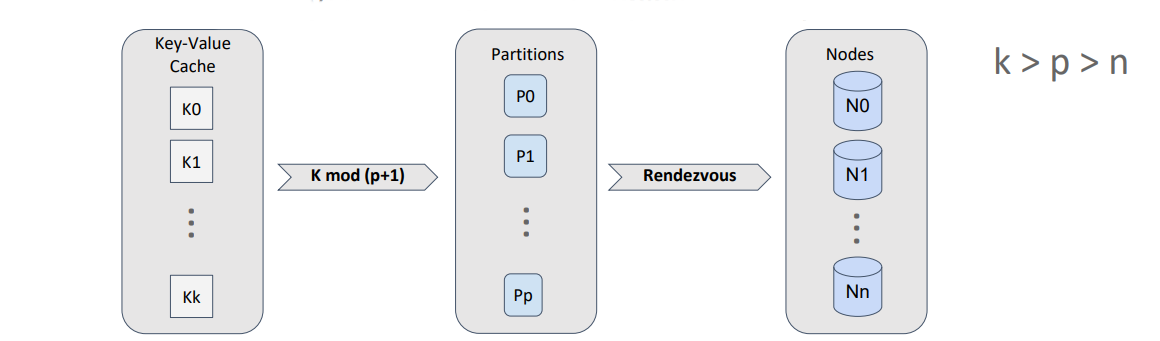
Т.к. количество партиций для кэша — это константа, то мы можем рассчитать распределение партиций по узлам один раз и закэшировать результат до тех пор, пока топология не будет изменена.
Каждый узел рассчитывает это распределение независимо, но на всех узлах при одинаковых входных данных это распределение будет идентичным.
Партиция может иметь несколько копий, мы их называем бэкапами. Основная партиция — называется праймари (primary) партицией.
Для наилучшего распределения ключей по партициям и партиций по узлам должно выполняться следующее правило: количество партиций должно быть значительно больше количества узлов, в свою очередь количество ключей должно быть значительно больше количества партиций.
Кэши в Ignite бывают партиционированные и реплицированные.
В партиционированном кэше количество бэкапов задается на этапе создания кэша. Партиции — праймари и бэкапы — равномерно распределены между узлами. Такой кэш лучше всего подходит для работы с оперативными данными, т.к. обеспечивает наилучшую производительность на запись, которая напрямую зависит от количества бэкапов. В общем случае чем больше бэкапов, тем больше узлов должны подтвердить запись ключа.
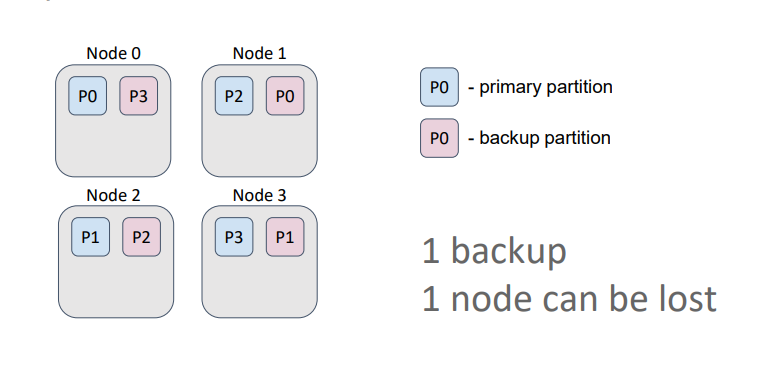
В данном примере кэш имеет один бэкап. Т.е. мы можем потерять один узел и при этом не потерять данные, т.к. бэкапы партиций никогда не хранятся на одном узле с праймари партицией или с другим ее бэкапом.
В реплицированном кэше количество бэкапов всегда равно количеству узлов топологии минус 1. Т.е. каждый узел всегда содержит копии всех партиций.
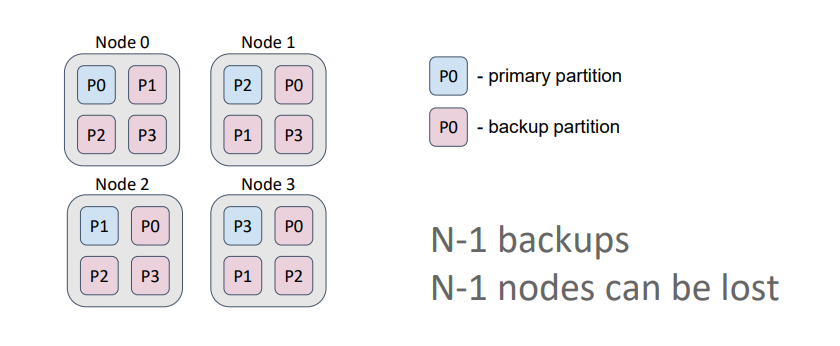
Такой кэш лучше всего подходит для работы с редко изменяемыми данными (например справочниками) и обеспечивает наибольшую доступность, т.к. мы можем потерять N-1 узлов (в данном случае 3), не потеряв данные. Также в этом варианте мы получим максимальную производительность на чтение, если позволим читать данные как из праймари партиций, так и из бэкапов.
Важное понятие, о котором нужно помнить для достижения наилучшей производительности — это колокация. Колокацией называют размещение каких-либо объектов в одном и том же месте. В нашем случае объекты — это хранимые в кэше сущности, а место — это узел.
Если объекты распределяются по партициям одной и той же аффинити функцией, то логично, что объекты с одинаковым аффинити-ключом попадут в одну и ту же партицию, а значит, на один и тот же узел. В Ignite это называется колокацией по аффинити.
По умолчанию аффинити-ключ — это первичный ключ объекта. Но в Ignite в качестве аффинити-ключа можно использовать любое другое поле объекта.
Колокация существенно снижает количество данных, пересылаемых между узлами для выполнения вычислений или SQL-запросов, что естественно ведет к уменьшению времени, затрачиваемого на выполнение этих задач. Рассмотрим это понятие на примере.
Пусть наша модель данных состоит из двух сущностей: заказ (Order) и позиция заказа (OrderItem). Одному заказу может соответствовать множество позиций. Идентификаторы заказов и позиций независимы, но позиция имеет внешний ключ, ссылающийся на соответствующий заказ.
Допустим, нам нужно выполнить некоторую задачу, которая должна для каждого заказа выполнить расчеты по позициям этого заказа.
По умолчанию аффинити-ключ — это первичный ключ. Поэтому заказы и позиции будут распределены между узлами в соответствии с их первичными ключами, которые, напомню, независимы.
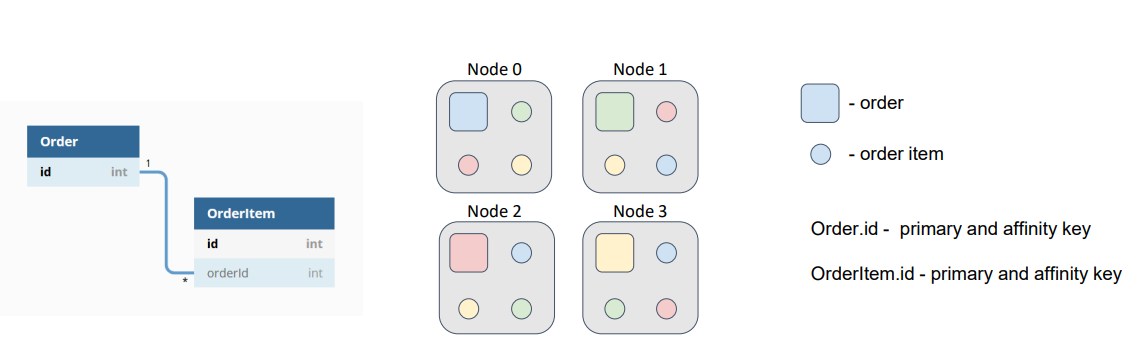
На схеме заказы представлены квадратами, а позиции кругами. Цвет говорит о принадлежности позиции к заказу.
При таком распределении данных наша гипотетическая задача будет отправлена на узел, где расположен искомый заказ, а затем ей потребуется зачитать позиции со всех остальных узлов, либо отправить на эти узлы подзадачу и получить результат вычислений. Это лишнее сетевое взаимодействие, которого можно и нужно избегать.
Что если мы подскажем Ignite, что позиции заказов нужно разместить на тех же узлах, что и сами заказы, т.е. сколоцируем данные?
В качестве аффинити-ключа для позиции мы возьмем внешний ключ OrderId и именно это поле будем использовать при вычислении партиции, которой принадлежит запись. При этом внутри партиции мы всегда сможем найти наш объект по первичному ключу.
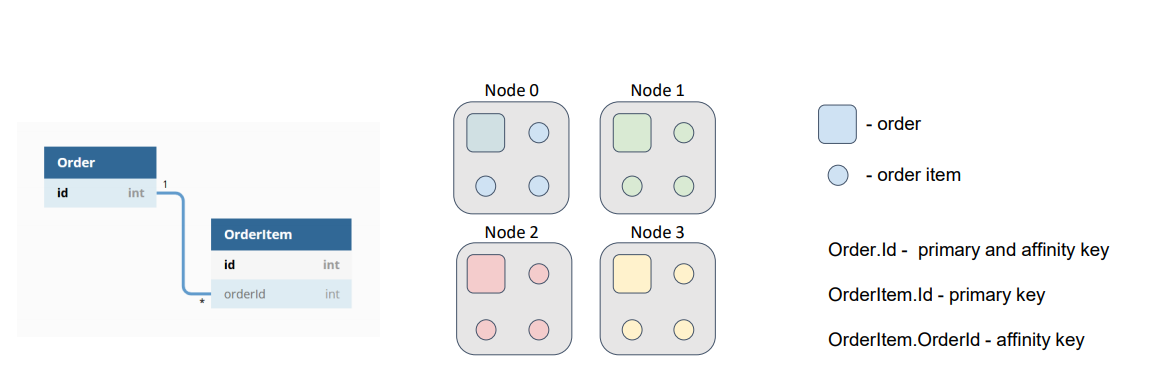
Теперь, если оба кэша (Order и OrderItem) используют одинаковую аффинити функцию с одинаковыми параметрами, наши данные будут находиться рядом и нам не потребуется ходить по сети за позициями заказов.
В текущей реализации объект аффинити-функции является параметром конфигурации кэша.
Сама аффинити-функция при создании принимает следующие аргументы:
Эти параметры не могут быть изменены.
С количеством партиций и бэкапов вроде все ясно. Про бэкап фильтр и флаг excludeNeighbors я расскажу чуть позже.
Во время выполнения аффинити-функция на вход получает текущую топологию кластера — по сути список узлов кластера — и рассчитывает распределение партиций по узлам в соответствии с примерами, которые я показывал, когда говорил об алгоритме rendezvous hashing.
Что касается бэкап-фильтра, то это предикат, который позволяет запретить аффинити-функции назначать бэкап партиции узлу, для которого предикат вернул значение false.
В качестве примера предположим, что наши физические узлы — серверы — расположены в дата-центре в разных стойках. Обычно каждая стойка имеет свое независимое питание…
… и если мы потеряем стойку, то потеряем и данные.
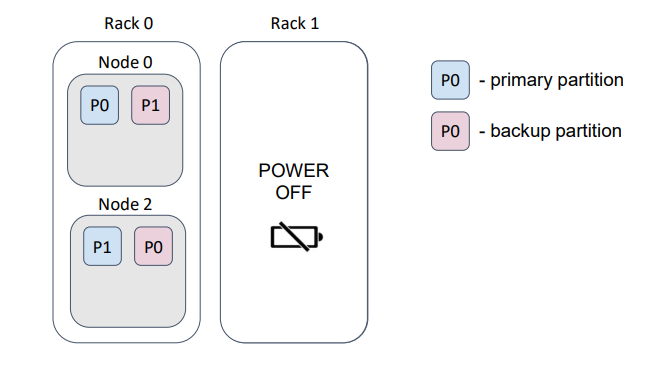
В данном примере мы потеряли половину партиций.
Но если мы зададим правильный бэкап-фильтр, то и распределение изменится таким образом…
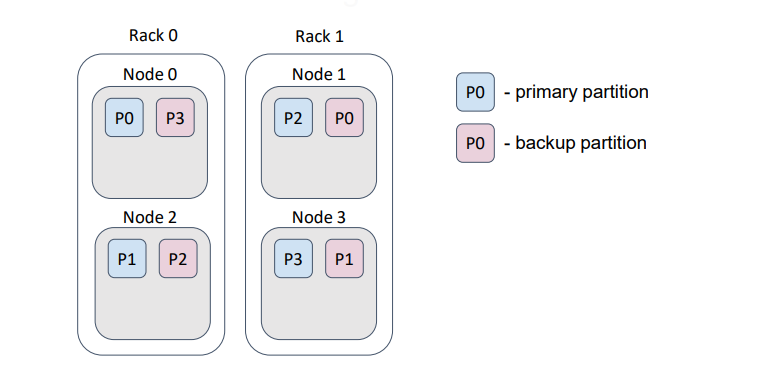
… что при потере стойки не произойдет потери данных и они все еще будут доступны.

Похожую функцию выполняет флаг excludeNeighbors и по сути он является сокращением для одного конкретного случая.
Нередко несколько узлов Ignite запускаются на одном физическом хосте. Этот случай очень похож на пример со стойками в датацентре, только теперь мы боремся с потерей данных при потере хоста, а не стойки.
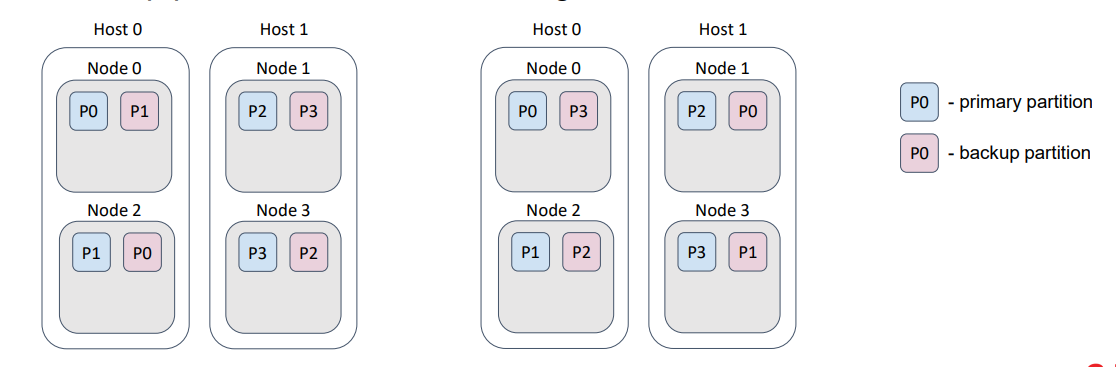
В остальном все то же самое. Можно реализовать это поведение с помощью бэкап-фильтра. Этот флаг является историческим наследием и может быть удален в следующем мажорном релизе Ignite.
Кажется, я рассказал об аффинити-функции и распределении данных все, что необходимо знать разработчику, использующему Apache Ignite.
В завершение давайте рассмотрим пример распределения 16 партиций по топологии из 3-х узлов. Для простоты и наглядности считаем, что у партиций нет бэкапов.
Я просто взял и написал маленький тест, который вывел мне реальное распределение:

Как видите, равномерность распределения не идеальная. Но погрешность будет заметно ниже с ростом количества узлов и партиций. Главное правило, которое необходимо соблюдать, это чтобы количество партиций было существенно больше, чем количество узлов. Сейчас в Ignite количество партиций для партиционированного кэша по умолчанию равно 1024.
Теперь добавим в топологию новый узел.
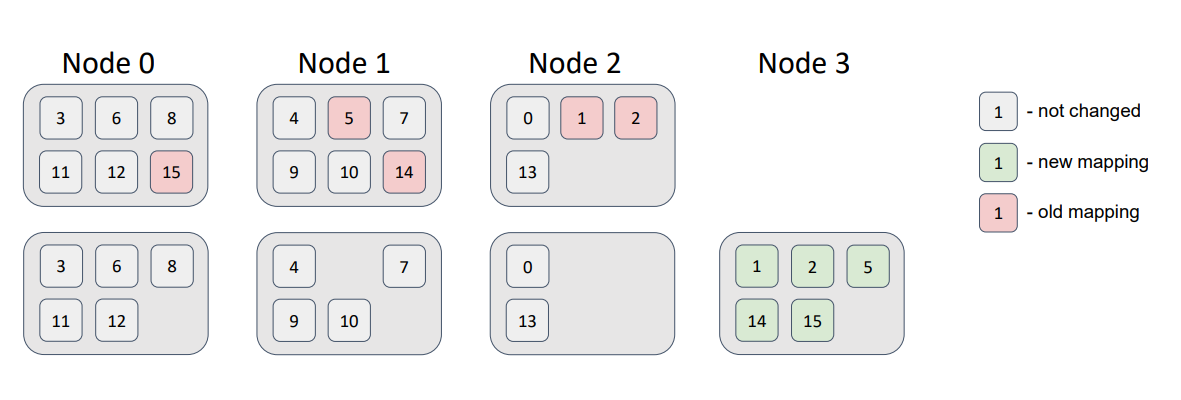
Часть партиций переехало на него. При этом требование минимального изменения распределения было соблюдено: новый узел получил часть партиций, а другие узлы партициями не обменивались.
Удалим из топологии узел, который присутствовал в ней на начальном этапе:
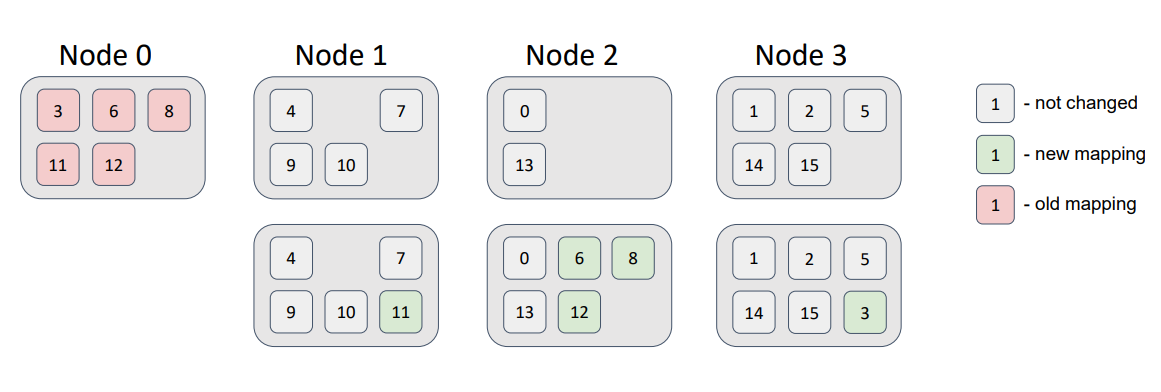
Теперь все партиции, которые были связаны с нулевым узлом, перераспределились по другим узлам топологии, не нарушая наших требований к распределению.
Как видите, в основе решения сложных задач зачастую лежат довольно тривиальные, хотя и не совсем очевидные идеи. Описанные решения используются в большинстве распределенных баз данных и неплохо справляются со своей задачей. Но решения эти рандомизированы и поэтому равномерность распределения далека от идеала. Можно ли улучшить равномерность без ущерба производительности и другим требованиям к распределению? Вопрос остается открытым.
Зачем вообще нужно что-то распределять
Довольно стандартная история развития любой системы требующей хранения данных и их обработки — это достижение некоторого потолка. Либо данных становится очень много и они физически не помещаются на устройство хранения, либо нагрузка растет такими темпами, что один сервер больше не в состоянии обрабатывать такое количество запросов. Нередки случаи, когда происходит и то и другое.
Как правило приходят к одному из двух решений: либо это шардирование имеющегося хранилища, либо переход на распределенную базу данных. Оба решения имеют ряд общих черт, самая очевидная из которых — это использование более чем одного узла для работы с данными. Далее множество узлов я буду называть топологией.
Проблема распределения данных по узлам топологии может быть сформулирована в виде набора требований, которым наше распределение должно удовлетворять:
- Необходим алгоритм, который позволит всем узлам топологии и клиентским приложениям прийти к одинаковому выводу о том, на каком узле или узлах находится некоторый объект (или ключ).
- Равномерность распределения. Чем равномернее данные распределены между узлами, тем равномернее будет распределена и нагрузка на эти узлы. Здесь я делаю допущение, что наши узлы обладают примерно одинаковыми ресурсами.
- Минимальное изменение распределения. При изменении топологии вследствие отказа узла, изменения в распределении должны коснуться только данных, расположенных на этом узле. Дополнительно нужно отметить, что при включении нового узла в топологию, не должно происходить обмена данными между узлами, которые уже были в топологии.
Достичь выполнения первых двух требований достаточно легко.
Знакомый всем подход, часто применяемый при балансировке нагрузки между функционально эквивалентными серверами, деление по модулю N, где N — это количество узлов в топологии и мы имеем взаимно-однозначное соответствие между номером узла и его идентификатором. Тогда все что нам нужно сделать, это представить ключ объекта в виде числового значения с помощью хэш-функции и взять от полученного значения остаток от деления на N.

На схеме отображено распределение 16-ти ключей по 3-м узлам. Видно, что это распределение равномерно, а алгоритм получения узла для объекта прост и гарантирует, что если все узлы топологии будут использовать этот алгоритм, то для одного и того же ключа и одного и того же N будет получен один и тот же результат.
Но что будет, если мы введем в топологию 4-ый узел?

Наша функция изменилась, теперь мы берем остаток от деления на 4, а не на 3. А если изменилась функция, то изменилось и распределение, причем очень сильно.
Здесь красным цветом показано предыдущее местоположение объектов для предыдущей версии топологии из трех узлов, а зеленым соответственно положение объектов для новой версии топологии из четырех узлов. Это очень похоже на привычный многим diff файлов, только вместо файлов у нас узлы.
Легко увидеть, что данные переместились не только на новый узел, но и произошел обмен данными между узлами, которые уже были в топологии. Т.е. мы наблюдаем паразитный трафик между узлами и требование минимального изменения распределения не выполняется.
Два популярных способа решения проблемы распределения данных с учетом перечисленных требований, следующие:
- Консистентное хэширование (consistent hashing).
- Алгоритм наибольшего случайного веса (HRW), также известный как Rendezvous hashing.
Оба этих алгоритма очень просты. Их описания на Википедии укладываются в несколько предложений. Хотя их все-таки трудно назвать очевидными. Интересующимся рекомендую почитать оригинальные статьи Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web и A Name-BasedMapping Scheme for Rendezvous. Наиболее понятно, на мой взгляд, идея алгоритма консистентного хэширования донесена в этом стэндфорском курсе.
Давайте рассмотрим эти алгоритмы более подробно.
Консистентное хэширование
Хитрость, лежащая в основе алгоритма консистентного хэширования, состоит в том, чтобы и узлы и хранимые объекты отобразить на одно и тоже пространство идентификаторов. Это делает наши, казалось бы разные сущности, объекты и узлы, сравнимыми.
Для получения такого отображения будем просто применять одну и ту же хэш-функцию к ключам объектов и к идентификаторам узлов. Результат хэш-функции для узла будем называть токеном, это нам пригодится позже.
Представим наше пространство идентификаторов в виде окружности, т.е. просто будем считать, что за максимальным значением идентификатора сразу же следует минимальное значение идентификатора.
Теперь для того, чтобы определить на каком узле живет объект, нужно получить значение хэш-функции от его ключа, а затем просто двигаться по окружности по часовой стрелке, пока не встретим на пути токен какого-либо узла. Направление движения неважно, но оно должно быть фиксированным.
Воображаемое движение по часовой стрелке функционально эквивалентно бинарному поиску по отсортированному массиву токенов узлов.

На схеме каждый сектор отдельного цвета отражает пространство идентификаторов, за которое ответственен конкретный узел.
Если мы добавим новый узел, то…

… он разделит один из секторов на две части и полностью заберет на себя соответствующие ключи.
В данном примере узел 3 забрал на себя часть ключей узла 1.
Как видите, этот подход дает довольно неравномерное распределение объектов по узлам, т.к. он сильно зависим от идентификаторов самих узлов. Как можно улучшить этот подход?
Можно назначить узлам не один, а несколько токенов (обычно это сотни). Добиться этого можно например введением множества хэш-функций для узла (по одной на токен) или многократным последовательным применением одной и той же хэш-функции к токену, полученному на предыдущем шаге. Но нужно не забывать о коллизиях. Не должно быть двух узлов с одинаковым токеном.

В данном примере каждый узел имеет 4 токена.
Что еще важно упомянуть: если мы хотим обеспечить сохранность данных в случае выхода какого-либо узла из топологии, то нам нужно хранить ключи на нескольких узлах (т.н. репликах или бэкапах). В случае алгоритма консистеного хэширования репликами будут следующие N-1 узлов на окружности, где N — это фактор репликации. Конечно порядок узлов должен определяться по конкретному токену (например по первому), т.к. при использовании множества токенов для каждого из них порядок расположения узлов может отличаться. Обратите внимание на схему: в ней нет четкого паттерна повторения узлов.
Что касается требования минимального изменения распределения при изменении топологии, то оно выполняется из-за того, что взаимный порядок узлов на окружности неизменен. Т.е. удаление узла из топологии не изменит отношение порядка между оставшимися узлами.
Rendezvous hashing
Алгоритм Rendezvous hashing кажется еще более простым, чем консистентное хэширование. В основе алгоритма лежит тот же принцип неизменности отношения порядка. Но вместо того, чтобы делать сравнимыми и узлы и объекты, мы делаем сравнимыми лишь узлы для конкретного объекта. Т.е. мы определяем отношение порядка между узлами для каждого объекта независимо.
Помогает нам в этом опять же хэширование. Но теперь, для того, чтобы определить вес узла N для данного объекта O, мы смешаем идентификатор объекта с идентификатором узла и возьмём хэш уже от этого микса. Проделав эту операцию для каждого узла мы получим набор весов, по которым и отсортируем узлы.
Узел, оказавшийся первым и будет отвечать за хранение объекта.
Так как все узлы топологии используют одни и те же входные данные, результат для них будет идентичным. Что удовлетворяет первому требованию.

Рассмотрим пример. Здесь у нас определено отношение порядка между тремя узлами для четырех различных ключей. Желтым обозначен узел с наибольшим весом, т.е. тот узел который будет в итоге отвечать за конкретный ключ.
Добавим еще один узел в топологию.

Я намеренно поместил его в диагональ, чтобы учесть все возможные варианты. Здесь узел 3, обозначенный зеленым цветом, вошел в топологию. Следовательно, развесовка узлов для каждого из ключей изменилась. Красным цветом обозначены узлы, которые изменили свое местоположение в списке для конкретного ключа, т.к. веса этих узлов оказались меньше, чем вес добавленного узла. При этом данное изменение повлияло лишь на один из ключей, K3.
Давайте вероломно выведем узел из топологии.

Вновь изменения коснулись лишь одного ключа, на этот раз K1. Остальные объекты не пострадали. Причиной тому, как и в случае с консистентным хэшированием, является неизменность отношения порядка между любой парой узлов. Т.е. требование минимального изменения распределения выполняется и не наблюдается паразитного трафика между узлами.
Распределение для rendezvous выглядит довольно хорошо и не требует дополнительных ухищрений по сравнению с консистентным хэшированием вроде токенов.
В случае, если мы хотим поддержать репликацию, то следующий в списке узел будет первой репликой для объекта, следующий узел второй репликой и т.д.
Как rendezvous hashing используется в Apache Ignite
За распределение данных в Apache Ignite отвечает так называемая аффинити-функция (см. интерфейс AffinityFunction). Реализация по-умолчанию — rendezvous hashing (см. класс RendezvousAffinityFunction).
Первое, на что нужно обратить внимание, это то, что Apache Ignite не отображает хранимые объекты напрямую на узлы топологии. Вместо этого вводится дополнительное понятие — партиция.
Партиция является контейнером для объектов и единицей репликации. Кроме того, количество партиций для конкретного кэша (это аналог таблицы в привычных нам базах данных) задается на этапе конфигурирования и не изменяется в течении жизненного цикла кэша.
Таким образом мы можем отображать объекты на партиции, используя эффективное деление по модулю, а для отображения партиций на узлы использовать rendezvous hashing.

Т.к. количество партиций для кэша — это константа, то мы можем рассчитать распределение партиций по узлам один раз и закэшировать результат до тех пор, пока топология не будет изменена.
Каждый узел рассчитывает это распределение независимо, но на всех узлах при одинаковых входных данных это распределение будет идентичным.
Партиция может иметь несколько копий, мы их называем бэкапами. Основная партиция — называется праймари (primary) партицией.
Для наилучшего распределения ключей по партициям и партиций по узлам должно выполняться следующее правило: количество партиций должно быть значительно больше количества узлов, в свою очередь количество ключей должно быть значительно больше количества партиций.
Кэши в Ignite бывают партиционированные и реплицированные.
В партиционированном кэше количество бэкапов задается на этапе создания кэша. Партиции — праймари и бэкапы — равномерно распределены между узлами. Такой кэш лучше всего подходит для работы с оперативными данными, т.к. обеспечивает наилучшую производительность на запись, которая напрямую зависит от количества бэкапов. В общем случае чем больше бэкапов, тем больше узлов должны подтвердить запись ключа.

В данном примере кэш имеет один бэкап. Т.е. мы можем потерять один узел и при этом не потерять данные, т.к. бэкапы партиций никогда не хранятся на одном узле с праймари партицией или с другим ее бэкапом.
В реплицированном кэше количество бэкапов всегда равно количеству узлов топологии минус 1. Т.е. каждый узел всегда содержит копии всех партиций.

Такой кэш лучше всего подходит для работы с редко изменяемыми данными (например справочниками) и обеспечивает наибольшую доступность, т.к. мы можем потерять N-1 узлов (в данном случае 3), не потеряв данные. Также в этом варианте мы получим максимальную производительность на чтение, если позволим читать данные как из праймари партиций, так и из бэкапов.
Колокация данных в Apache Ignite
Важное понятие, о котором нужно помнить для достижения наилучшей производительности — это колокация. Колокацией называют размещение каких-либо объектов в одном и том же месте. В нашем случае объекты — это хранимые в кэше сущности, а место — это узел.
Если объекты распределяются по партициям одной и той же аффинити функцией, то логично, что объекты с одинаковым аффинити-ключом попадут в одну и ту же партицию, а значит, на один и тот же узел. В Ignite это называется колокацией по аффинити.
По умолчанию аффинити-ключ — это первичный ключ объекта. Но в Ignite в качестве аффинити-ключа можно использовать любое другое поле объекта.
Колокация существенно снижает количество данных, пересылаемых между узлами для выполнения вычислений или SQL-запросов, что естественно ведет к уменьшению времени, затрачиваемого на выполнение этих задач. Рассмотрим это понятие на примере.
Пусть наша модель данных состоит из двух сущностей: заказ (Order) и позиция заказа (OrderItem). Одному заказу может соответствовать множество позиций. Идентификаторы заказов и позиций независимы, но позиция имеет внешний ключ, ссылающийся на соответствующий заказ.
Допустим, нам нужно выполнить некоторую задачу, которая должна для каждого заказа выполнить расчеты по позициям этого заказа.
По умолчанию аффинити-ключ — это первичный ключ. Поэтому заказы и позиции будут распределены между узлами в соответствии с их первичными ключами, которые, напомню, независимы.

На схеме заказы представлены квадратами, а позиции кругами. Цвет говорит о принадлежности позиции к заказу.
При таком распределении данных наша гипотетическая задача будет отправлена на узел, где расположен искомый заказ, а затем ей потребуется зачитать позиции со всех остальных узлов, либо отправить на эти узлы подзадачу и получить результат вычислений. Это лишнее сетевое взаимодействие, которого можно и нужно избегать.
Что если мы подскажем Ignite, что позиции заказов нужно разместить на тех же узлах, что и сами заказы, т.е. сколоцируем данные?
В качестве аффинити-ключа для позиции мы возьмем внешний ключ OrderId и именно это поле будем использовать при вычислении партиции, которой принадлежит запись. При этом внутри партиции мы всегда сможем найти наш объект по первичному ключу.

Теперь, если оба кэша (Order и OrderItem) используют одинаковую аффинити функцию с одинаковыми параметрами, наши данные будут находиться рядом и нам не потребуется ходить по сети за позициями заказов.
Конфигурация аффинити-функции в Apache Ignite
В текущей реализации объект аффинити-функции является параметром конфигурации кэша.
Сама аффинити-функция при создании принимает следующие аргументы:
- Количество партиций;
- Количество бэкапов (на самом деле это тоже конфигурационный параметр кэша);
- Фильтр бэкапов;
- Флаг excludeNeighbors.
Эти параметры не могут быть изменены.
С количеством партиций и бэкапов вроде все ясно. Про бэкап фильтр и флаг excludeNeighbors я расскажу чуть позже.
Во время выполнения аффинити-функция на вход получает текущую топологию кластера — по сути список узлов кластера — и рассчитывает распределение партиций по узлам в соответствии с примерами, которые я показывал, когда говорил об алгоритме rendezvous hashing.
Что касается бэкап-фильтра, то это предикат, который позволяет запретить аффинити-функции назначать бэкап партиции узлу, для которого предикат вернул значение false.
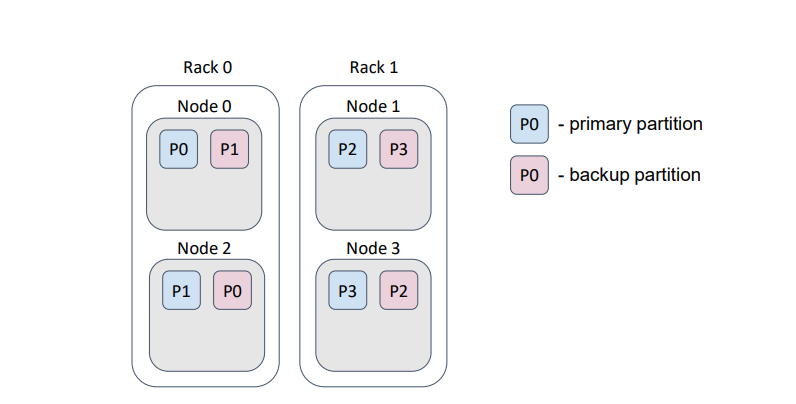
В качестве примера предположим, что наши физические узлы — серверы — расположены в дата-центре в разных стойках. Обычно каждая стойка имеет свое независимое питание…

… и если мы потеряем стойку, то потеряем и данные.

В данном примере мы потеряли половину партиций.
Но если мы зададим правильный бэкап-фильтр, то и распределение изменится таким образом…

… что при потере стойки не произойдет потери данных и они все еще будут доступны.

Похожую функцию выполняет флаг excludeNeighbors и по сути он является сокращением для одного конкретного случая.
Нередко несколько узлов Ignite запускаются на одном физическом хосте. Этот случай очень похож на пример со стойками в датацентре, только теперь мы боремся с потерей данных при потере хоста, а не стойки.

В остальном все то же самое. Можно реализовать это поведение с помощью бэкап-фильтра. Этот флаг является историческим наследием и может быть удален в следующем мажорном релизе Ignite.
Кажется, я рассказал об аффинити-функции и распределении данных все, что необходимо знать разработчику, использующему Apache Ignite.
В завершение давайте рассмотрим пример распределения 16 партиций по топологии из 3-х узлов. Для простоты и наглядности считаем, что у партиций нет бэкапов.
Я просто взял и написал маленький тест, который вывел мне реальное распределение:

Как видите, равномерность распределения не идеальная. Но погрешность будет заметно ниже с ростом количества узлов и партиций. Главное правило, которое необходимо соблюдать, это чтобы количество партиций было существенно больше, чем количество узлов. Сейчас в Ignite количество партиций для партиционированного кэша по умолчанию равно 1024.
Теперь добавим в топологию новый узел.

Часть партиций переехало на него. При этом требование минимального изменения распределения было соблюдено: новый узел получил часть партиций, а другие узлы партициями не обменивались.
Удалим из топологии узел, который присутствовал в ней на начальном этапе:

Теперь все партиции, которые были связаны с нулевым узлом, перераспределились по другим узлам топологии, не нарушая наших требований к распределению.
Как видите, в основе решения сложных задач зачастую лежат довольно тривиальные, хотя и не совсем очевидные идеи. Описанные решения используются в большинстве распределенных баз данных и неплохо справляются со своей задачей. Но решения эти рандомизированы и поэтому равномерность распределения далека от идеала. Можно ли улучшить равномерность без ущерба производительности и другим требованиям к распределению? Вопрос остается открытым.