Потому что во многой мудрости много печали;
И кто умножает познания, умножает скорбь.
• Екклесиаст 1:18

Данная статья не может служить поводом для выражения нетолерантности или дискриминации по какому-либо признаку.
В первой части статьи я только лишь обозначил проблему, которая звучала следующим образом: вероятность быть одинокой/одиноким зависит от имени человека. Более корректно было бы использовать слово корреляция, однако я все же позволю себе некоторую лингвистическую вольность еще раз в этом вопросе и буду надеятся на то, что все понимают это утверждение правильно. Тем не менее, я хотел бы поблагодарить всех за комментарии к моей предыдущей статье.
В одном из комментариев я говорил о том, что вполне возможно, есть некоторый третий фактор, который коррелирует c именем и одиночеством. В качестве иллюстрации я привел пример с яблоками: положим, что одиночество зависит от того, сколько яблок ест девушка, и по какой-то причине девушки с именем Катя едят больше яблок, чем с имеем Маша. Понятно, что для каждой конкретной Маши или Кати это не значит ровным счетом ничего, но в среднем выходит, что одни одиноки более, чем другие, из-за того, что едят яблоки в разном количестве.
На самом деле проблема сводится к другой ровно такой же: почему люди с одним именем едят яблок больше, чем другие? Однако объяснение этой корреляции может оказаться более простым.
Cherry picking и статистическая значимость
Прежде чем я продолжу, я сделаю несколько замечаний по поводу выборки в предыдущей статье, потому что мы продоложим с ней работать. С одной стороны, я действительно предпочитаю качественные аргументы. С другой стороны, я понимаю людей, который задают вопрос почему выборка была именно такой и статистически значимы ли результаты. Я сознательно ничего не писал про статистическую значимость, потому что ситуация, когда два "случайных" процесса ведут себя одинаково в разных системах, с разными людьми и механикой постановки статуса кажется мне совершенно невероятной. Что касается выбора имен, тут есть элемент случайности (я старался брать не только имена своих знакомых девушек, но и заполнять недостающие в частотном смысле части распределения), но я не делал ничего специально, кроме ограничения себя в количестве, а полученная таблица содержала 3 стабильные части совершенно независимо от моего желания.
Однако, по просьбе трудящихся (как написано в одном из комментариев), я взял 100 абсолютно случайных имен, для которых было достаточно статистики в Одноклассниках и проверил, что будет если перемешать сами имена. Если бы я получил точно такое же распределение (после подсчета u), как предсказывали некоторые люди, то можно было бы говорить, что результат статистически не значим и в лучшем случае можно говорить о зависимости лишь от частоты имени. Однако тест Манна-Уитни показал p-value = 0.000256, т.е. начальное распределение и то, что получилось при перемешивании — совершенно разные вещи.
Поэтому я и дальше буду использовать изначальные таблицы, считая их в достаточной степени репрезентативными для нашего исследования.
У меня будут проблемы с вами, Бонд?
Мой опыт работы в СПбГУ натолкнул меня на следующую мысль (мне кажется, она посетила не меня одного): а что если более умные люди более одиноки? То есть весь этот диалог между Бондом и Веспер на картинке из фильма Казино Рояль — это своего рода тавтология в вероятностном смысле.
Хорошо известно, что IQ тесты не очень репрезентативны, да и померить IQ на прямую в социальной сети не представляется возможным. Но мы можем сделать следующее предположение: люди, которые имеют высшее образование, в среднем более умные, чем те, кто его не имеют. Конечно, это так себе критерий, потому что высшее образование есть почти у всех. Поэтому можно попробовать взять более или менее элитные учебные заведения, но такие, чтобы diversity по специализации было достаточно хорошим. Поэтому мы попробуем сделать следующее: для города Санкт-Петербург мы посмотрим распределение имен среди студентов СПбГУ, а для Москвы — соответственно среди студентов МГУ. Это опять же спекулятивное предположение, но в среднем оно вполне жизнеспособно для наших целей.
Сделаем следующее: просто найдем тех, кто учился в СПбГУ и МГУ с заданным именем и поделим на число всех с таким именем в нужном городе. По правде говоря, имя Лейла тут стоило бы убрать, т.е. оно имеет некоторую "региональную специфику", но для полноты картины мы ничего трогать не будем.
Давайте посмотрим, что же получилось и сравним с теми таблицами по городам Санкт-Петербург и Москва, что я сделал для предыдущей статьи:
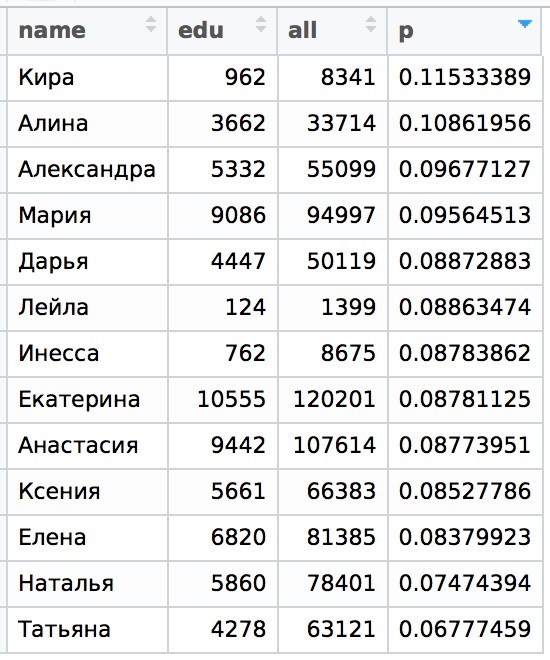
Здесь p = edu / all, т.е. доля девушек с данным именем (согласно статистике ВКонтакте), которые учились или учатся в СПбГУ в общем объеме людей с таким же именем в Санкт-Петербурге.
Теперь тоже самое для МГУ:
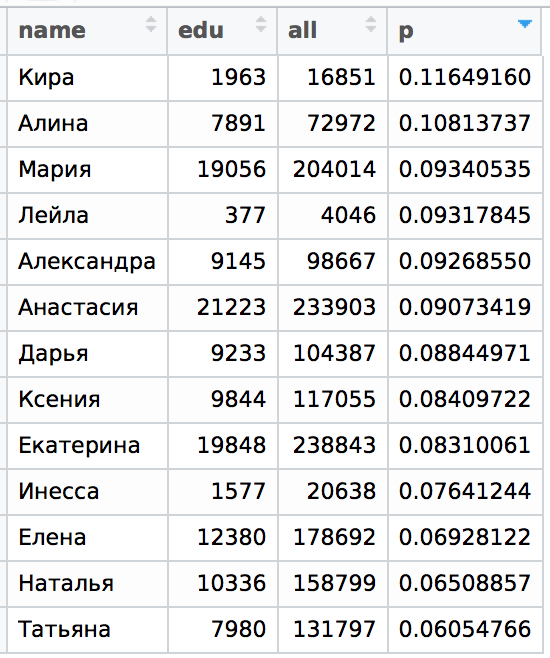
Давайте еще раз взглянем для сравнения на таблицы из предыдущей статьи. Вот распределение по Санкт-Петербургу (q — это унифицированный показатель "одиночества", полный спектр обозначений можно найти в первой части статьи).
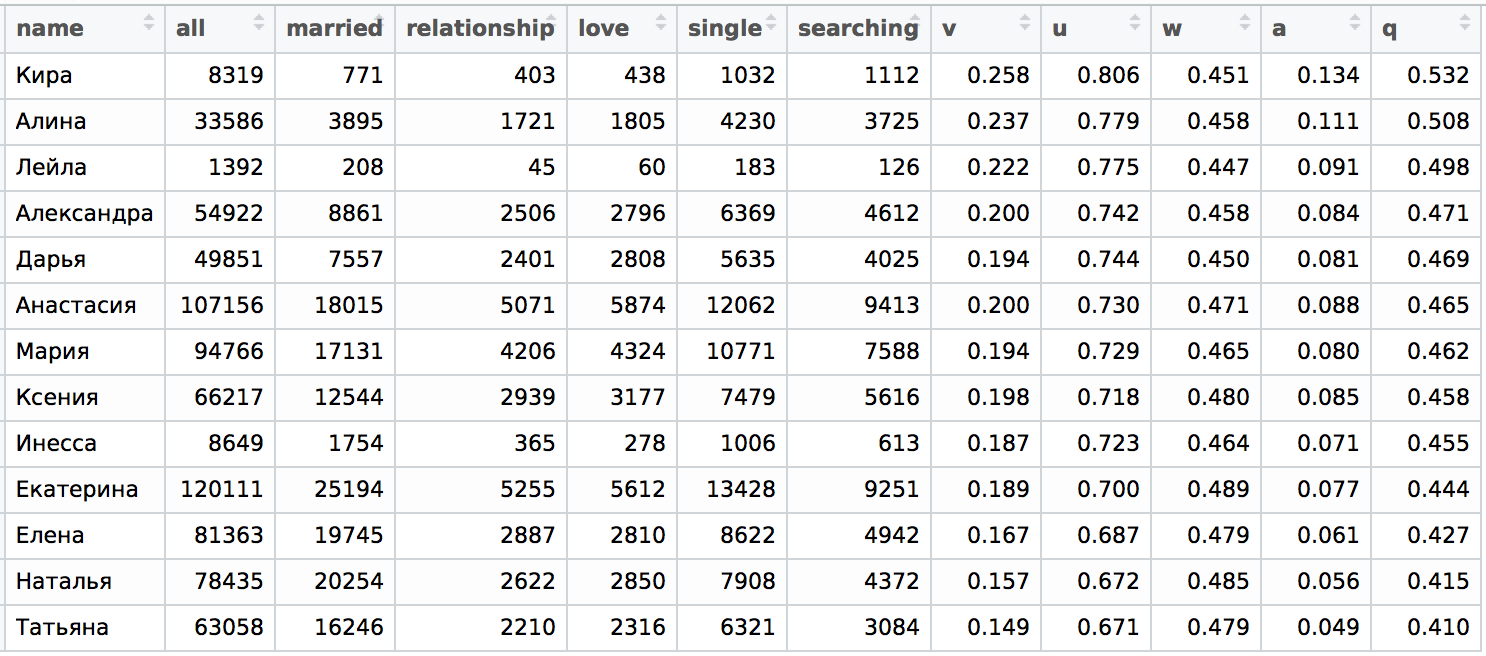
Для Москвы распределение выглядит следующим образом:
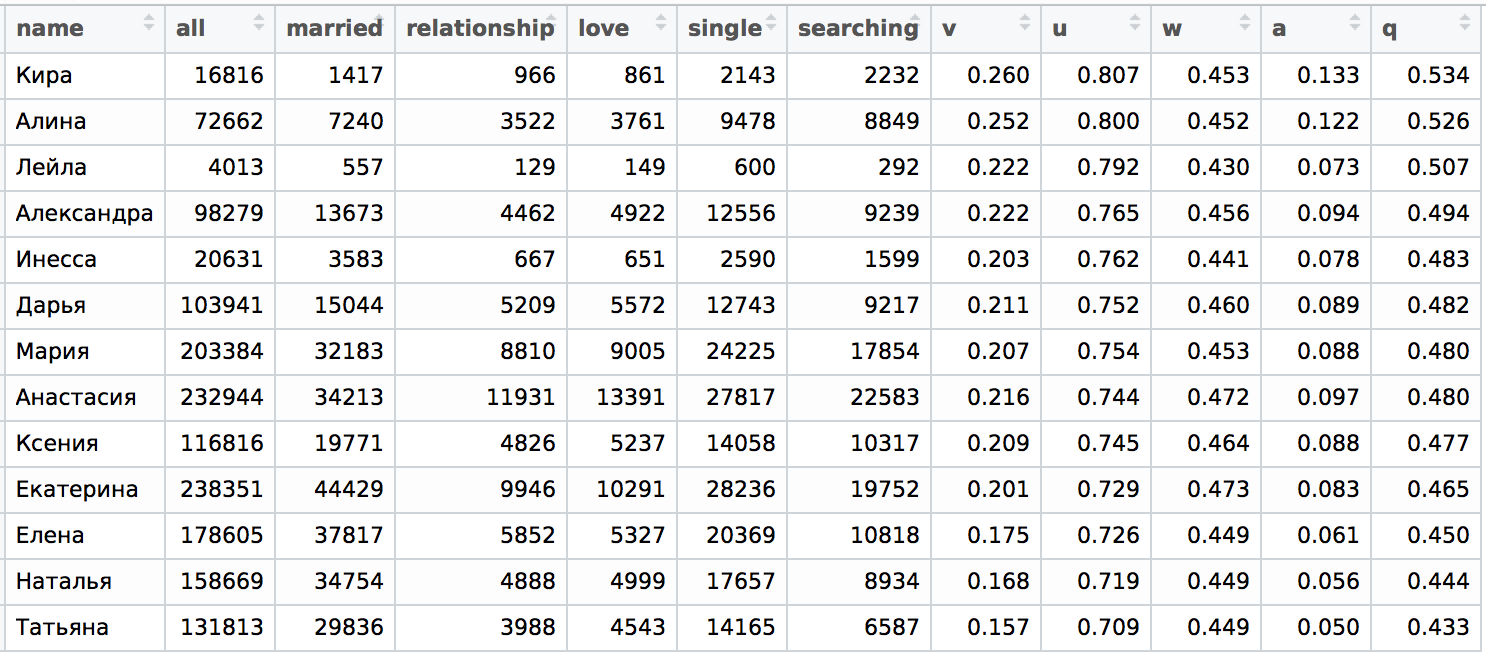
Видно, что по крайней мере верхняя и нижняя часть таблицы при сортировке по p и q более или менее совпадают, средняя немного перемешана, но каких-то существенных перестановок между частями не наблюдается. В случае имени Инессы есть некоторое несовпадение, для точного анализа нужно было бы отделить имя Инна и Инесса и посмотреть детали распределения по Москве и Санкт-Петербургу. Но здесь мы этого делать не будем, ограничимся лишь качественной оценкой. Для этого построим "зависимость" q от p для случая Санкт-Петербурга:
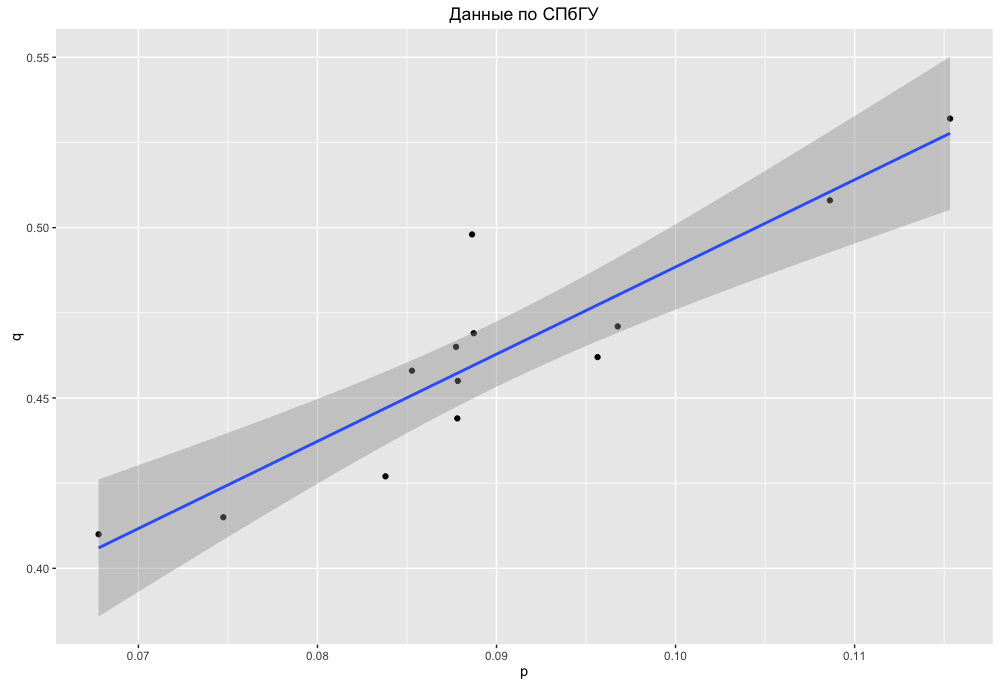
Теперь такой же график для МГУ:

То есть выходит так, что более умные и хорошо образованные девушки более одиноки. Это все конечно условно, и возможно например, что это лишь означает более поздний брак.
Рейтинг университетов
На самом деле, если есть корреляция между одиночеством и хорошим образованием, то, наверное, одиночество можно считать некоторой мерой качества образования и интеллекта (конечно, в вероятностном смысле). Поэтому я взял несколько хороших университетов, которые смог сходу вспомнить (и которые с некоторым трудом мне удалось найти в поиске в ВК) и решил посчитать для них те самые показатели q, u и v, которые в прошлой статье я сосчитал для множества имен. Как и в случае имен я взял и сделал сортировку по q (в качестве дополнительного параметра я посчитал diversity d = all / (all + all_m) по гендерному признаку, где all_m — это количество молодых людей в университете):
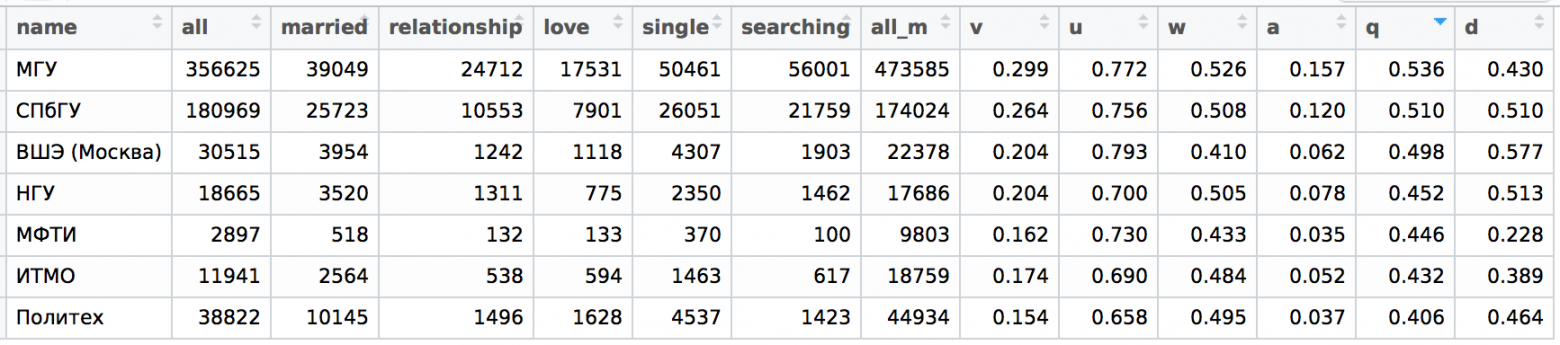
Вам это ничего не напоминает? Правильно, если погуглить рейтинг университетов, то можно найти следующее (это верхушка национального рейтинга):
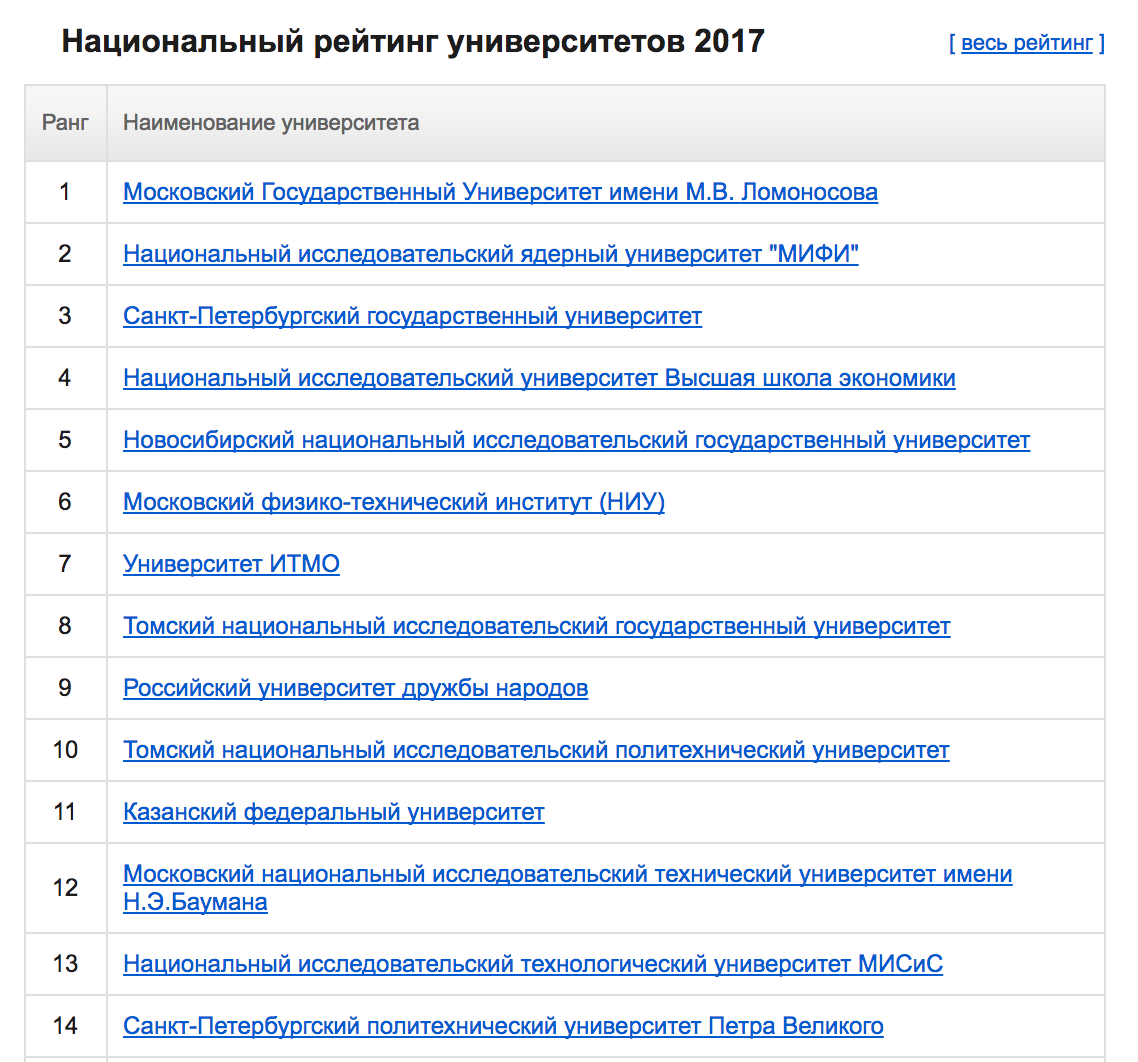
Кто хочет увидеть полный рейтинг, тому сюда: Национальный рейтинг университетов 2017. Конечно в моей таблице не все ВУЗы, и для университетов с низким рейтингом это так не работает (к примеру, для РГПУ им. Герцена), однако это точно заставляет задуматься.
Вместо заключения
Трудно сказать, насколько сильно мы приблизились к пониманию происходящего. Однако корреляция между образованием и одиночеством уже не выглядит так безумно, как корреляция между именем и одиночеством.
Здесь я использовал данные Одноклассников только для проверки статистической значимости результатов предыдущей статьи, а все остальное было построено целиком на данных ВКонтакте.