Finite State Entropy (FSE) – алгоритм энтропийного кодирования, чем-то похожий и на алгоритм Хаффмана, и на арифметическое кодирование. При этом он взял лучшее от них обоих: работает так же быстро, как хаффмановский, и со степенью сжатия как у арифметического кодирования.
FSE принадлежит семейству кодеков ANS (Asymmetric Numeral Systems), изобретённых Яреком Ду́дой. На основе его исследований Ян Колле разработал оптимизированный вариант алгоритма, впоследствии названный FSE.
В заметках Яна Колле непросто разобраться, поэтому я изложу объяснение в несколько ином порядке, более удобном для понимания, на мой взгляд.

Вспомним, как работает алгоритм Хаффмана.
Пусть у нас есть некое сообщение, состоящее из символов в следующих пропорциях:
С таким удачным распределением можно закодировать символы следующим образом:

Для A понадобится 1 бит, для B – 2 бита; C и D – по 3 бита.
Если распределение вероятностей окажется не столь подходящим, например:
A: 40%; B: 30%; C: 15%; D: 15%, то по алгоритму Хаффмана мы получим точно такие же коды символов, но сжатие при этом будет уже не столь хорошим.
Степень сжатия сообщения описывается следующей формулой: , где
, где
Известно, что для энтропийных кодеков оптимальное качество сжатия описывается формулой Шеннона: . Если сравнить это с предыдущей формулой, то получается, что
. Если сравнить это с предыдущей формулой, то получается, что  . Чаще всего величина этого логарифма получается нецелой.
. Чаще всего величина этого логарифма получается нецелой.
В алгоритме Хаффмана число бит округляется до целого, что негативно сказывается на степени сжатия.
В алгоритме арифметического кодирования используется другой подход, позволяющий не округлять и тем самым приблизиться к «идеальному» сжатию. Но он работает сравнительно медленно.
Алгоритм FSE – нечто среднее между предыдущими двумя подходами. В нём для кодирования символа используется переменное число бит (иногда больше, иногда меньше) так, чтобы в среднем получалось бит на символ.
бит на символ.
Рассмотрим пример. Пусть в кодируемом сообщении символы встречаются в следующей пропорции:
A: 5; B: 5; C: 3; D: 3
Назовём эти числа нормализованными частотами и обозначим
 – сумма (нормализованных) частот символов.
– сумма (нормализованных) частот символов.
В нашем примере N = 16. Для быстрой работы алгоритма необходимо, чтобы N было степенью двойки. Если сумма частот символов не равна степени двойки (почти всегда), то частоты нужно нормализовать – пропорционально уменьшить (или увеличить) их так, чтобы в сумме получилась степень двойки. Подробнее об этом будет сказано позднее.
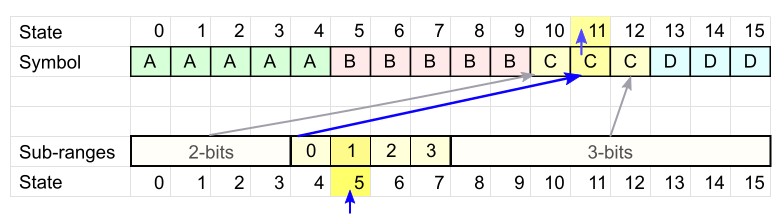
Возьмём таблицу из N колонок и впишем туда символы сообщения так, чтобы каждый символ встречался ровно столько раз, какая у него частота. Порядок пока не важен.
Каждому символу А сопоставим свой диапазон ячеек (Sub-ranges на рисунке): размер каждого диапазона должен быть степенью двойки (для быстродействия), в сумме они должны покрывать все N ячеек (пока что нам не важно, как расположены эти диапазоны).
Аналогично для каждого из остальных символов определяем свой набор диапазонов.
Для символа D будет 3 диапазона:

Кодовая таблица готова. Закодируем с её помощью слово «BCDA».
Декодирование выполняется в обратном порядке – от последнего закодированного символа к первому.
Теория говорит нам, что кодирование будет оптимальнее, если одинаковые символы распределены по таблице более равномерно.

Это нужно для того, чтобы состояние не «застаивалось» в больших интервалах, теряя лишний бит.
Может показаться, что неплохо было бы неплохо всё время попадать в маленькие интервалы (в левой части таблицы). Но в этом случае уже другие символы будут чаще попадать в большие интервалы – в итоге получится только хуже.
Наконец, перейдём от теории к коду. Для начала разберёмся, как во время кодирования рассчитать, в какой интервал попадает текущее состояние и сколько бит потребуется записать.
Для кодирования нам нужно разбить таблицу размером N (равным некоторой степени двойки) на
Например, если N = 16 и нам нужно 6 интервалов, то разбиение будет: 2+2+2+2+4+4 – четыре «малых» интервала размером 21 и два «больших» размером 22.

Достаточно просто вычислить размер большого интервала – это наименьшая степень двойки, такая что
Соответственно,
Вернёмся к получению
Теперь найдем, при каком условии состояние state попадает в большой интервал.
Чтобы определить границу между малыми и большими интервалами, умножим количество малых интервалов на их размер:
Получается, что состояние
Размер интервала, в который мы попали, определяет, сколько младших бит от текущего состояния нужно записать при кодировании. Если условие выше выполняется, то
Вместо операции сравнения применим хак со сдвигом разности на достаточно большое число:
Отсутствие условия в данном выражении позволяет процессору эффективнее задействовать внутренний параллелизм. (Переменная count соответствует символу q в предыдущих формулах.)
В итоге, функция кодирования приобретает следующий вид:
Всё, что можно рассчитать заранее, выносим в таблицу:
Заметим, что
Как видите, вычисления очень простые и быстрые.
Декодирование будет выглядеть соответственно:
Ещё проще!
Реальный код можно посмотреть здесь. Там же можно найти, как заполняются таблицы
Выше мы исходили из предположения, что сумма частот символов
При этом нужно принять во внимание, что сумма частот символов равна размеру кодовой таблицы. Чем больше таблица, тем точнее будут представлены частоты символов и тем лучше будет сжатие. С другой стороны, сама таблица тоже занимает много места. Для оценки размера сжатых данных можно использовать формулу Шеннона ,
, чересчур смело предполагая, что сжатие стремится к идеалу, и таким способом подобрать оптимальные таблицы.
В процессе нормализации частот может возникнуть множество мелких проблем. Например, если у некоторых символов очень-очень маленькая вероятность, то наименьшая представимая частота 1 / N может оказаться слишком неточным приближением, но меньше уже никак. Один из подходов в этом случае – сразу назначить таким символам
Существуют как быстрые эвристические алгоритмы нормализации частот, так и медленные, но более точные. Выбор за вами.
Давайте рассмотрим ситуацию, когда нам нужно кодировать числовые значения из потенциально большого диапазона, например, от -65536 до +65535. При этом вероятностное распределение этих чисел сильно неравномерное: с большим пиком в центре и очень маленькими вероятностями по краям, как на картинке. Если кодировать каждое значение отдельным символом, то таблица будет невообразимого размера.
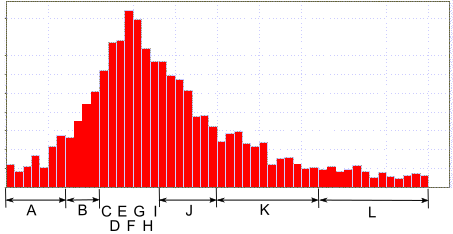
В такой ситуации можно обозначить одним символом целый диапазон значений. При помощи FSE будем кодировать только сам символ, а смещение в диапазоне будем записывать «как есть», по размеру диапазона.
Такой приём позволяет сделать кодовые таблицы более-менее компактными.
Этот пример демонстрирует, что выбор алфавита сильно зависит от ваших данных. Нужно применить немного фантазии, чтобы кодирование получилось наиболее оптимальным.
Если у разных частей данных разное частотное распределение, то для их кодирования лучше использовать разные таблицы.
При этом разнородные данные можно кодировать, поочерёдно используя разные таблицы! Состояние из одной таблицы используется для кодирования следующего символа другой таблицей. Главное, чтобы вы смогли повторить тот же порядок при декодировании. Таблицы также должны быть одинакового размера.
К примеру, пусть ваши данные – это последовательность вида "команда – число – команда – число…". Вы всегда знаете, что после команды будет идти число, и это определяет порядок использования таблиц.
Если кодировать данные от конца к началу, то при декодировании (от начала к концу) будет понятно, что за чем будет идти и, соответственно, какую таблицу использовать для декодирования следующего элемента.
Как уже упоминалось выше, кодовую таблицу нужно сохранять вместе с данными, чтобы их декодировать. При этом желательно, чтобы таблица не занимала много места.
Давайте посмотрим, какие поля есть в таблице dTable:
Итого: 4 байта на каждый символ. Немало.
Но если подумать, вместо таблицы dTable можно хранить лишь нормализованные частоты символов. К примеру, если размер кодовой таблицы будет 28 = 256, то 8 бит на символ будет более чем достаточно.
Зная частоты, можно построить точно такой же dTable, как при кодировании.
При этом советую убедиться, что в алгоритме не используется float (с ним бывают различия на разных процессорах, лучше использовать fixed point), применять только stable_sort и тому подобные меры для надёжной воспроизводимости результата.
Кстати, и эти таблицы тоже можно как-нибудь сжать. ;)
Мы в компании Playrix используем FSE для кодирования векторных анимаций. Дельты между кадрами состоят из множества маленьких значений с пиком распределения около нуля. Переход с Хаффмана на FSE позволил уменьшить размер анимаций примерно в полтора раза. В памяти хранятся сжатые данные, распаковка делается «на лету» с одновременным воспроизведением. FSE позволяет делать это очень эффективно.
Теперь, когда вы разобрались, как работает FSE, для большего понимания рекомендую прочитать подробности в блоге Яна Колле (на английском):
Код на GitHub (автор Ян Колле): https://github.com/Cyan4973/FiniteStateEntropy.
FSE принадлежит семейству кодеков ANS (Asymmetric Numeral Systems), изобретённых Яреком Ду́дой. На основе его исследований Ян Колле разработал оптимизированный вариант алгоритма, впоследствии названный FSE.
В заметках Яна Колле непросто разобраться, поэтому я изложу объяснение в несколько ином порядке, более удобном для понимания, на мой взгляд.

Сравнение с существующими алгоритмами
Вспомним, как работает алгоритм Хаффмана.
Пусть у нас есть некое сообщение, состоящее из символов в следующих пропорциях:
A: 50%; B: 25%; C: 12.5%; D: 12.5%
С таким удачным распределением можно закодировать символы следующим образом:

Для A понадобится 1 бит, для B – 2 бита; C и D – по 3 бита.
Если распределение вероятностей окажется не столь подходящим, например:
A: 40%; B: 30%; C: 15%; D: 15%, то по алгоритму Хаффмана мы получим точно такие же коды символов, но сжатие при этом будет уже не столь хорошим.
Степень сжатия сообщения описывается следующей формулой:
pi – с какой частотой символ встречается в сообщении, bi – количество бит для кодирования этого символа.Известно, что для энтропийных кодеков оптимальное качество сжатия описывается формулой Шеннона:
bi должно быть равно Нецелое число бит – что с этим делать?
В алгоритме Хаффмана число бит округляется до целого, что негативно сказывается на степени сжатия.
В алгоритме арифметического кодирования используется другой подход, позволяющий не округлять и тем самым приблизиться к «идеальному» сжатию. Но он работает сравнительно медленно.
Алгоритм FSE – нечто среднее между предыдущими двумя подходами. В нём для кодирования символа используется переменное число бит (иногда больше, иногда меньше) так, чтобы в среднем получалось
Как работает FSE
Рассмотрим пример. Пусть в кодируемом сообщении символы встречаются в следующей пропорции:
A: 5; B: 5; C: 3; D: 3
Назовём эти числа нормализованными частотами и обозначим
qi.В нашем примере N = 16. Для быстрой работы алгоритма необходимо, чтобы N было степенью двойки. Если сумма частот символов не равна степени двойки (почти всегда), то частоты нужно нормализовать – пропорционально уменьшить (или увеличить) их так, чтобы в сумме получилась степень двойки. Подробнее об этом будет сказано позднее.
Возьмём таблицу из N колонок и впишем туда символы сообщения так, чтобы каждый символ встречался ровно столько раз, какая у него частота. Порядок пока не важен.
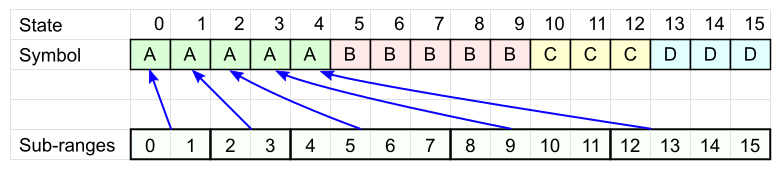
Каждому символу А сопоставим свой диапазон ячеек (Sub-ranges на рисунке): размер каждого диапазона должен быть степенью двойки (для быстродействия), в сумме они должны покрывать все N ячеек (пока что нам не важно, как расположены эти диапазоны).
Аналогично для каждого из остальных символов определяем свой набор диапазонов.
Для символа D будет 3 диапазона:
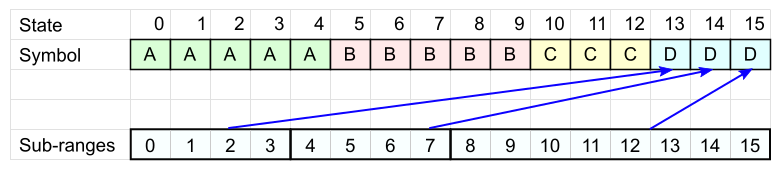
Кодовая таблица готова. Закодируем с её помощью слово «BCDA».
- Первый символ – "B". Выберем любую ячейку таблицы с этим символом. Номер ячейки – наше текущее состояние.

Текущее состояние = 5.
- Возьмём следующий символ – "C". Смотрим кодовую таблицу для C и проверяем, в какой из интервалов попало наше текущее состояние.

В нашем случае состояние 5 попало во второй интервал.
Записываем смещение от начала этого интервала. В нашем случае оно равно 1. Для записи смещения понадобится 2 бита – по размеру диапазона, в который попало наше состояние.
Текущий диапазон соответствует символу C в ячейке 11, значит новое состояние = 11.
- Повторяем пункт 2 для каждого последующего символа: выбираем нужную таблицу, определяем диапазон, записываем смещение, получаем новое состояние.
Для каждого символа записывается лишь смещение в интервале. Для этого используется разное число бит – в зависимости от того, в «большой» или «маленький» интервал мы попадём. В среднем, количество бит на символ будет стремиться к значению. Доказательство этого факта требует сложной теории, поэтому просто поверьте.
- Когда будет закодирован последний символ, у нас останется конечное состояние. Его нужно сохранить, с него будет начинаться декодирование.
Декодирование выполняется в обратном порядке – от последнего закодированного символа к первому.
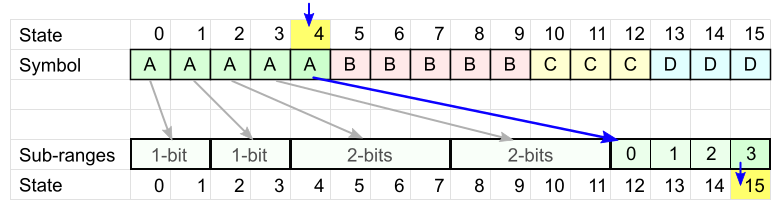
- У нас есть конечное состояние (4), и оно однозначно определяет последний закодированный символ (A).
- Каждое состояние соответствует интервалу в кодовой таблице. Считываем требуемое число бит по размеру интервала (2 бит) и получаем новое состояние (15), которое определяет следующий символ.
- Повторяем пункт 2, пока не декодируем все символы.
Декодирование заканчивается, либо когда заканчиваются закодированные данные, либо когда встречается специальный стоп-символ (требует дополнительного символа в алфавите).
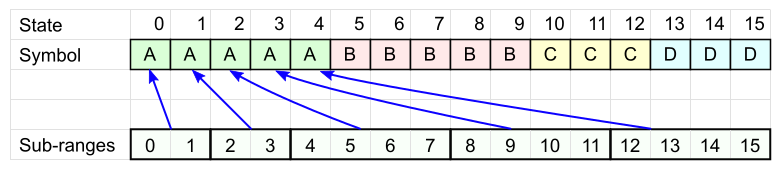
Распределение символов в таблице
Теория говорит нам, что кодирование будет оптимальнее, если одинаковые символы распределены по таблице более равномерно.
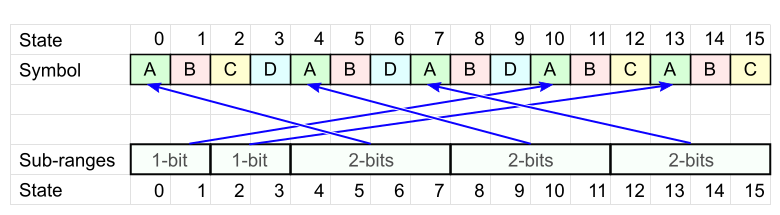
Это нужно для того, чтобы состояние не «застаивалось» в больших интервалах, теряя лишний бит.
Может показаться, что неплохо было бы неплохо всё время попадать в маленькие интервалы (в левой части таблицы). Но в этом случае уже другие символы будут чаще попадать в большие интервалы – в итоге получится только хуже.
Оптимизация
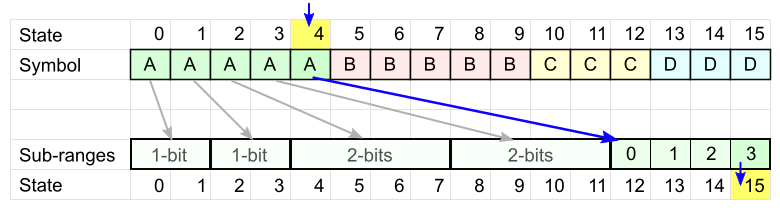
Наконец, перейдём от теории к коду. Для начала разберёмся, как во время кодирования рассчитать, в какой интервал попадает текущее состояние и сколько бит потребуется записать.
Для кодирования нам нужно разбить таблицу размером N (равным некоторой степени двойки) на
qi интервалов. Размеры этих интервалов тоже будут степени двойки: 2^maxbit и 2^(maxbit-1) – назовём их «большие» и «малые». Пусть малые интервалы находятся слева, а большие – справа, как на рисунке ниже.Например, если N = 16 и нам нужно 6 интервалов, то разбиение будет: 2+2+2+2+4+4 – четыре «малых» интервала размером 21 и два «больших» размером 22.

Достаточно просто вычислить размер большого интервала – это наименьшая степень двойки, такая что
2^maxbit >= N / q.Соответственно,
maxbit = log2(N) - highbit(q), где highbit – номер старшего ненулевого бита.Вернёмся к получению
q интервалов. Сначала поделим таблицу на «большие» интервалы: (N / 2^maxbit) штук, затем несколько из них разделим пополам. Разделение интервала увеличивает их общее количество на 1, поэтому «поделить» потребуется q - (N / 2^maxbit) больших интервалов. Соответственно, количество малых интервалов будет (q - (N / 2^maxbit))*2.Теперь найдем, при каком условии состояние state попадает в большой интервал.
Чтобы определить границу между малыми и большими интервалами, умножим количество малых интервалов на их размер:
(q - (N / 2^maxbit))*2 * 2^(maxbit-1) = (q * 2^maxbit) - N;Получается, что состояние
state попадает в большой интервал при условииN + state >= q * 2^maxbit, иначе – в малый.Размер интервала, в который мы попали, определяет, сколько младших бит от текущего состояния нужно записать при кодировании. Если условие выше выполняется, то
nbBitsOut = maxbit, в противном случае (maxbit - 1). Остальные биты состояния будут определять номер интервала.Вместо операции сравнения применим хак со сдвигом разности на достаточно большое число:
nbBitsOut = ((maxbit << 16) + N + state - (count << maxbit)) >> 16;Отсутствие условия в данном выражении позволяет процессору эффективнее задействовать внутренний параллелизм. (Переменная count соответствует символу q в предыдущих формулах.)
В итоге, функция кодирования приобретает следующий вид:
// Рассчитываем количество бит для записи
nbBitsOut = ((maxBitsOut << 16) + N + state - (count << maxBitsOut)) >> 16;
// Записываем nbBitsOut младших бит от state в bitStream:
bitStream.WriteBits(state, nbBitsOut);
interval_number = (N + state) >> nbBitsOut;
// новое состояние:
state = nextStateTable[deltaFindState[symbol] + interval_number];
Всё, что можно рассчитать заранее, выносим в таблицу:
symbolTT[symbol].deltaNbBits = (maxBitsOut << 16) - (count << maxBitsOut);Заметим, что
state всё время используется в виде N + state. Если в nextStateTable тоже хранить N + next_state, то функция примет следующий вид:nbBitsOut = (N_plus_state + symbolTT[symbol].deltaNbBits) >> 16;
bitStream.WriteBits(N_plus_state, nbBitsOut);
// новое состояние:
N_plus_state = nextStateTable[symbolTT[symbol].deltaFindState + (N_plus_state >> nbBitsOut)];
Как видите, вычисления очень простые и быстрые.
Декодирование будет выглядеть соответственно:
// Записываем декодированный символ
outputSymbol(decodeTable[state].symbol);
// Берём из таблицы, сколько бит надо прочитать
nbBits = decodeTable[state].nbBits;
// Прочитанные биты определяют смещение в интервале
offset = readBits(bitStream, nbBits);
// Вычисляем следующее состояние: начало диапазона + смещение
state = decodeTable[state].subrange_pos + offset;Ещё проще!
Реальный код можно посмотреть здесь. Там же можно найти, как заполняются таблицы
symbolTT и decodeTable.О нормализации частот символов
Выше мы исходили из предположения, что сумма частот символов
qi равна степени двойки. В общем случае это, конечно же, не так. Тогда нужно пропорционально уменьшить эти числа, чтобы в сумме они давали степень двойки.При этом нужно принять во внимание, что сумма частот символов равна размеру кодовой таблицы. Чем больше таблица, тем точнее будут представлены частоты символов и тем лучше будет сжатие. С другой стороны, сама таблица тоже занимает много места. Для оценки размера сжатых данных можно использовать формулу Шеннона
В процессе нормализации частот может возникнуть множество мелких проблем. Например, если у некоторых символов очень-очень маленькая вероятность, то наименьшая представимая частота 1 / N может оказаться слишком неточным приближением, но меньше уже никак. Один из подходов в этом случае – сразу назначить таким символам
qi = 1, поместить их в конец кодовой таблицы (так оптимальнее), и затем разбираться с остальными символами. Округление значений к ближайшему целому тоже может оказаться не лучшим вариантом. Об этом и о множестве других нюансов хорошо написано у Яна Колле (1, 2, 3, 4).Существуют как быстрые эвристические алгоритмы нормализации частот, так и медленные, но более точные. Выбор за вами.
Выбор модели данных
Давайте рассмотрим ситуацию, когда нам нужно кодировать числовые значения из потенциально большого диапазона, например, от -65536 до +65535. При этом вероятностное распределение этих чисел сильно неравномерное: с большим пиком в центре и очень маленькими вероятностями по краям, как на картинке. Если кодировать каждое значение отдельным символом, то таблица будет невообразимого размера.
В такой ситуации можно обозначить одним символом целый диапазон значений. При помощи FSE будем кодировать только сам символ, а смещение в диапазоне будем записывать «как есть», по размеру диапазона.
Такой приём позволяет сделать кодовые таблицы более-менее компактными.
Этот пример демонстрирует, что выбор алфавита сильно зависит от ваших данных. Нужно применить немного фантазии, чтобы кодирование получилось наиболее оптимальным.
Смешанное кодирование
Если у разных частей данных разное частотное распределение, то для их кодирования лучше использовать разные таблицы.
При этом разнородные данные можно кодировать, поочерёдно используя разные таблицы! Состояние из одной таблицы используется для кодирования следующего символа другой таблицей. Главное, чтобы вы смогли повторить тот же порядок при декодировании. Таблицы также должны быть одинакового размера.
К примеру, пусть ваши данные – это последовательность вида "команда – число – команда – число…". Вы всегда знаете, что после команды будет идти число, и это определяет порядок использования таблиц.
Если кодировать данные от конца к началу, то при декодировании (от начала к концу) будет понятно, что за чем будет идти и, соответственно, какую таблицу использовать для декодирования следующего элемента.
О записи таблицы
Как уже упоминалось выше, кодовую таблицу нужно сохранять вместе с данными, чтобы их декодировать. При этом желательно, чтобы таблица не занимала много места.
Давайте посмотрим, какие поля есть в таблице dTable:
unsigned char symbol; // если алфавит не более 256 символов
unsigned short subrange_pos; // начало соответствующего интервала
unsigned char nbBits; // сколько бит прочитать
Итого: 4 байта на каждый символ. Немало.
Но если подумать, вместо таблицы dTable можно хранить лишь нормализованные частоты символов. К примеру, если размер кодовой таблицы будет 28 = 256, то 8 бит на символ будет более чем достаточно.
Зная частоты, можно построить точно такой же dTable, как при кодировании.
При этом советую убедиться, что в алгоритме не используется float (с ним бывают различия на разных процессорах, лучше использовать fixed point), применять только stable_sort и тому подобные меры для надёжной воспроизводимости результата.
Кстати, и эти таблицы тоже можно как-нибудь сжать. ;)
Эпилог
Мы в компании Playrix используем FSE для кодирования векторных анимаций. Дельты между кадрами состоят из множества маленьких значений с пиком распределения около нуля. Переход с Хаффмана на FSE позволил уменьшить размер анимаций примерно в полтора раза. В памяти хранятся сжатые данные, распаковка делается «на лету» с одновременным воспроизведением. FSE позволяет делать это очень эффективно.
Ссылки
Теперь, когда вы разобрались, как работает FSE, для большего понимания рекомендую прочитать подробности в блоге Яна Колле (на английском):
- Finite State Entropy — A new breed of entropy coder
- FSE decoding: how it works
- Huffman, a comparison with FSE
- A comparison of Arithmetic Encoding with FSE
- FSE: Defining optimal subranges
- FSE: distributing symbol values
- FSE decoding: wrap up
- FSE encoding: how it works
- FSE tricks — Memory efficient subrange maps
- Better normalization, for better compression
- Perfect Normalization
- Ultra-fast normalization
- Taking advantage of unequalities to provide better compression
- Counting bytes fast — little trick from FSE
Код на GitHub (автор Ян Колле): https://github.com/Cyan4973/FiniteStateEntropy.