Блог компании Специальный Технологический Центр
Разберём, как можно выбрать исполнительные двигатели для своего проекта, самоделки и иных целей. Будет использоваться подход к синтезу, который получил название синтеза цифровой системы по ее непрерывному аналогу. Начальным этапом процесса проектирования является выполнение энергетического расчёта и выбор на этой основе исполнительных двигателей, механических передач и силовых преобразователей (усилителей мощности), в совокупности обеспечивающих возможность реализации силового воздействия на объект управления.
1. Энергетический расчёт.
Целью энергетического расчета является рациональный выбор исполнительных элементов приводов системы, которые обладают энергетическими возможностями для обеспечения механического объекта управления по заданному закону во всех предусмотренных режимах работы. Задача энергетического расчета состоит в анализе сил (моментов сил) и скоростей, которые должны развивать приводы системы и выборе исполнительных элементов, энергетически обеспечивающих возможность получения требуемых сил и скоростей движения механических объектов управления и удовлетворяющих заданным критериям эффективности такого выбора.
Считаем, что динамическая жёсткость приводов бесконечно высока и поэтому взаимовлияние степеней подвижности манипулятора не проявляется. Тогда можно считать, что при движении одного из звеньев второе звено остаётся неподвижным.
Примем себе техническое задание:
Спроектировать привода для двухзвенного плоского манипулятора робота. Возьмём для этого упрощенную модель двухзвенного механизма манипулятора (рис.1), имеющего "плечевое" и "локтевое" звенья, причем рабочий орган (РО) условно считается закрепленным непосредственно на конце "локтевого" звена.

На рисунке приняты обозначения:
q1 и q2 - обобщённые координаты манипуляционного механизма. Они представляют собой углы поворота "плечевого" и "локтевого" звеньев манипулятора, соответственно. Угол q1 определяется как отклонение "плечевого" звена от вертикали, а угол q2 определяется как отклонение "локтевого" звена от продольной оси "плечевого" звена. Положительные значения этих углов соответствуют вращению звеньев по часовой стрелке;
L1 и L2 - длины «плечевого» и «локтевого» звеньев, соответственно. L2 - расстояние от оси поворота "локтевого" звена до центра масс рабочего органа с объектом манипулирования;
m1 и m2 - массы «плечевого» и «локтевого» звеньев, соответственно.
Считается, что каждая из этих масс сосредоточена в центре соответствующего звена;
m0 - суммарная масса рабочего органа и объекта манипулирования;
mДВ1 и mДВ2 - массы исполнительных двигателей;
V и a - скорость и ускорение конечной точки манипулятора соответственно;
R - расстояние от оси вращения «плечевого» звена до конечной точки манипулятора;
M1 и M2 - моменты сил, развиваемые приводами и действующие на звенья манипулятора.
Таблица 1. Параметры манипуляционного механизма:
Параметр | условное обозначение | значение |
Длина "плечевого" звена манипуляционного механизма, м | L.1 | 0.8 |
Расстояние от оси поворота "локтевого" звена до центра масс рабочего органа с объектом манипулирования, м | L.2 | 0.2 |
Диапазон изменения перемещенй "плечевого" звена манипулятора, град | q.1 | -30… +120 |
Диапазон изменения " локтевого" звена манипулятора, град | q.2 | -60 … +120 |
Масса "плечевого" звена, кг | m1 | 20 |
Масса "локтевого" звена, кг | m2 | 15 |
Масса рабочего органа, кг | mс | 6 |
Масса объекта манипулирования, кг | mо | 2 |
Таблица 2. Основные требования к исполнительной системе робота:
Параметр | условное обозначение | значение |
Допустимая статическая погрешность рабочего органа, мм | ΔX.доп.ст | 0.05 |
Допустимая динамическая погрешность рабочего органа, мм | ΔX.доп.дин | 0.1 |
Максимальная скорость рабочего движения, м/с | V.p.max | 0.5 |
Максимальное ускорение рабочего движения, | а.p.max | 0.2 |
Максимальная скорость рабочего органа при «переброске», м/с | V.п.max | 0.75 |
Время разгона до максимальной скорости, с | t.раз | 0.3 |
Перерегулирование при малом ступенчатом воздействии, % | σ.доп | 0 |
Относительная длительность “переброски” в рабочем цикле, % | t.пер.отн | 0.3 |
1.1 Выбор двигателя и редуктора привода второго звена.
Кинематический анализ:
Найдём максимальные значения угловой скорости и углового ускорения для второго звена манипулятора.
Максимальное угловое ускорение 2-го звена:
Максимальная угловая скорость рабочего движения 2-го звена:
Максимальное угловое ускорение рабочего движения 2-го звена:

Максимальный суммарный момент сил M2max , который должен развивать привод второго звена, определяется по формуле.

η - КПД механической передачи.
Статический момент относительно оси вращения 2-го звена определяется по формуле:

где g =9.807 м/с2 - ускорение свободного падения.
Mст2 имеет максимальное значение при выполнении условия sin(q1+q2)=1. Mст2 = 30.4 Н*м.
Для вычисления динамического момента, действующего на второе звено, находим эквивалентный момент инерции Jэкв2 этого звена по формуле:
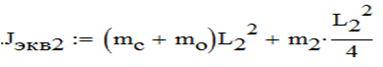
Jэкв2 = 0.62 кг*м2
Максимальное значение динамического момента (для режима переброски) получим:
С целью обеспечения точной работы приводов манипулятора могут быть
выбраны волновые или планетарные редукторы. Предварительно выбираем волновой редуктор HDUR-32 компании Harmonic drive gearing. По данным производителя КПД такого редуктора η2̗ = 0.85 В этом случае максимальный суммарный момент сил M2max , который должен развивать привод второго звена:
Оценка мощности двигателя второго звена:
Максимальное значение мощности механического движения второго звена:
Требуемую мощность двигателя второго звена P2 выбираем из условия.
P2≈(2...3)*P2max. P2= 420 Вт
Выбор исполнительного двигателя производим по требуемой мощности. Выбираем двигатель TETRA 85SR2.2, обладающий следующими параметрами:
Pн2 = 650 Вт - номинальная мощность.
Мн2 = 2.2 ̗- номинальный момент Н*м.
J дв2 =1.8Έ10˕4 кг*Ем2 - момент инерции ротора.
mдв2 = 4.2 кг - масса двигателя.
n2ном = 3000 об/мин - номинальная частота вращения.
Rя = 19.76 Ом - активное сопротивление якоря.
U2ном = 250 В - номинальное напряжение якоря.
Определение требуемого передаточного отношения и марки редуктора.
Оценка значения передаточного отношения редуктора привода второго звена:
Выбираем редуктор HDUR FDD-32-260, обладающий следующими параметрами:
iр2 = 260 - передаточное отношение.
mp2 ̗= 1.7 кг- масса редуктора.
Для дальнейших расчётов и выбора компонентов привода первого звена принимаем массу привода второго звена равной:
Теперь проверим выполнения необходимых условий правильности выбора
двигателя и редуктора. Проверяем выбранный двигатель по моменту:
Следовательно, подсистема «двигатель-редуктор» способна создавать момент, не меньше требуемого.
1.2 Выбор двигателя и редуктора привода первого звена.
Кинематический анализ манипуляционного механизма
Расчёты проводятся в соответствии с кинематической схемой и схемой действия сил, представленной на рис. 3

В таком положении момент М1 первого звена будет иметь значения, наиболее близкие к максимально возможным значениям. Скорость вращения первого звена Ω1 определяется по формуле:
где q2 - обобщённая координата, характеризующая положение второго звена
относительно продольной оси первого звена. Таким образом, видно, что скорость вращения первого звена Ω1 зависит от обобщенной координаты q2
Угловое ускорение, с которым движется первое звено, определяется по формуле:
Следовательно, угловое ускорение тоже зависит от q2.
Силовой анализ манипуляционного механизма.
Определяется момент сил, который должен развивать привод первого звена. При этом считаем, что силы приложены в центрах масс первого и второго звеньев, рабочего органа и объекта манипулирования
Статический момент Мст1 действующий относительно оси поворота первого звена, зависит от обобщённых координат:

Динамический момент Mдин1 , зависящий от углового ускорения ε1 и
эквивалентного момента инерции Jэкв1 вычисляется по формуле:

Эквивалентный момент инерции манипуляционного механизма, перемещаемого первым приводом, можно оценить по формуле:

где ρ - расстояние от оси вращения первого звена до центра масс второго звена, причём
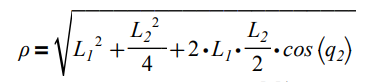
Максимальное значение суммарного момента М1 можно определить, варьируя значения переменных q1 и q2. Для упрощения решения задачи будем рассматривать конфигурацию манипулятора, представленную на рис. 3, при которой рабочий орган находится на горизонтальной прямой линии, проходящей через ось вращения первого звена. Тогда между переменными q1 и q2 будет существовать связь следующего вида:

КПД редуктора привода первого звена примем η1̗0.85
Оценка мощности механического движения первого звена.
Для определения максимального значения мощности механического движения первого звена воспользуемся графиком зависимости требуемой мощности P1 от обобщенной координаты q2.

P1max = 303 Вт. Примем q2pmax = 58 град.

1.3 Выбор двигателя привода первого звена.
Выбираем двигатель по мощности из расчета P1≈(2...3)*P1max. P1 = 2.5 * P1max = 757.5 Вт.
Выбираем двигатель ESA 3L обладающий следующими параметрами:
Pн1 = 800 Вт - номинальная мощность.
Мн1 = 1.75 Н*м - номинальный момент.
Jдв1 = 0.64 * 10^-4 кг*м^2 - момент инерции ротора.
Mдв1 = 3.05 кг – масса двигателя.
n1ном = 3000 об\мин - номинальная частота вращения.
Rя1 = 5.24 Ом - сопротивление якоря.
U1ном = 250 В - номинальное напряжение якоря.
Iяном = 2.5 А - номинальный ток якоря.
Tэ = 0.00275 - электромагнитная постоянная времени.
Вычислим номинальную угловую скорость двигателя:

Выбираем редуктор аналогичный редуктору второго звена HDUR-32-260
обладающий следующими параметрами:
i = 260 - передаточное отношение.
m 1.7 кг- масса редуктора.