Comments 24
Очень много опечаток: тире вместо дефисов, «статика» вместо «статистики» и так далее. Утверждение «если эти случайные величины не являются независимыми» — не верно. Случайные величины как раз должны быть iid (independent and identically distributed) — независимыми и имеющими одинаковое распределение. Увы, не знаком с русскоязычной терминологией.
+2
ну да, но в случае с монеткой или выборкой в t — тесте, это требование как и раз не выполняется.
+1
Броски идеальной «честной» монетки независимы в используемой модели. Кстати, для подобных случаев (два возможных исхода) существуют биномиальные тесты. t-тест используется для проверки гипотез относительно среднего значения при наличии iid случайных величин имеющих нормальное распределение с неизвестной дисперсией.
0
не независимыми являются рассчитанные отклонения от ожидаемых частот для орла и решки
0
Гипотезу, что монетка честная вы тестом проверить не можете, поэтому вы будете пытаться найти статистическое подтверждение тому, что она не честная («орёл» выпадает с вероятностью, отличной от 0,5) и в случае не отклонения нулевой гипотезы тестом станете считать, что у вас нет данных, подтверждающих нечестность монеты (что вовсе не равнозначно с её «честностью»). Так что же вам мешает взять точный биномиальный тест, который оптимально подходит для описываемой ситуации (100 iid бросков — это совершенно точно не «достаточно большое» количество) и что вы хотите сказать утверждением о «зависимости расчитанных отклонений» (языковой барьер, извиняюсь)?
0
Тут Вы конечно же правы, искать будем подтверждение именно альтернативной гипотезе! Собственно ничего не мешает, но это же пост не про оптимальный критерий работы с нечестными монетками, просто взял ее для примера, т.к. на двух исходах можно наглядно показать, почему несмотря на два слагаемых в формуле критерия мы используем распределение Хи — квадрат с df = 1.
0
t-распределение Студента, если мне не изменяет память, по определению, распределение частного, в котором в числителе величина, имеющая стандартное нормальное распределение а в знаменателе — квадратный корень из величины, имеющей хи-квадрат-распределение с n степенями свободы, поделённой на число степеней свободы. В модели с нормальным распределением с неизвестным стандартным отклонением мы используем несмещённую (unbiased) оценку (да простят меня за TeX) $\hat{\sigma} = \sqrt{\frac{1}{n-1}\sum_{i=0}^{n}{\big(X_i-\overline{X}\big)^2}}$ (версия, в которой n вместо n-1 — не является не смещённой) потому и она имеет t-распределение с n-1 степеней свободы. Могу ошибаться, но по-моему, так.
0
Хорошее замечание! Действительно в знаменателе стоит выборочная sd, распределение которой может быть описано:
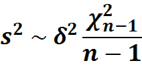
Но в процессе доказательства этого факта, мы сталкиваемся с n слагаемыми — для каждого наблюдения в выборке мы рассчитываем его квадрат отклонения от выборочного среднего. Но распределение этой суммы n слагаемых мы опишем распределение хи — квадрат с n — 1 степенью свободы.

Но в процессе доказательства этого факта, мы сталкиваемся с n слагаемыми — для каждого наблюдения в выборке мы рассчитываем его квадрат отклонения от выборочного среднего. Но распределение этой суммы n слагаемых мы опишем распределение хи — квадрат с n — 1 степенью свободы.
0
Это верно только для выборки из нормального распределения. И если у нас выборка из нормального распределения, то можно показать, что выборочное среднее и выборочная дисперсия будут независимыми, а выборочная дисперсия будет иметь \chi^2 распределение с n-1 степенью свободы.
0
И, кстати, ровно поэтому формула (\bar(x) — \mu) / sd / \sqrt(n) выше не верна. Т.к. нам нужно или же чтобы тут было не обычное стандартное отклонение, а корень из несмещенной оценки дисперсии («подправленное стандартное отклонение»), или же sqrt(n-1).
0
При росте размера выборки биномиальное распределение стремится к нормальному, этот факт подробно обсосан у Боровкова.
0
Случайные величины никому ничего не должны, они вполне могут быть зависимыми. Типичный пример: случайный x и случайная y = f(x), где f — непрерывная функция.
0
Никакой «магии» в степенях свободы нет, и никакого физического смысла это название не несет. Просто такое название, ага.
Ну и использовать t-критерий для проверки гипотезы о росте нельзя, т.к. ключевое предположение t-критерия о том, что у нас выборка из нормального распределения, не выполняется. Поэтому вероятность ошибки первого рода такого критерия будет отличаться от заданного уровня значимости, мощность будет непонятно какой, а полученным p-значениями верить нельзя. Разница будет особенно заметна на малых объемах выборки, ага.
Ну и использовать t-критерий для проверки гипотезы о росте нельзя, т.к. ключевое предположение t-критерия о том, что у нас выборка из нормального распределения, не выполняется. Поэтому вероятность ошибки первого рода такого критерия будет отличаться от заданного уровня значимости, мощность будет непонятно какой, а полученным p-значениями верить нельзя. Разница будет особенно заметна на малых объемах выборки, ага.
0
Да, согласен конечно, если подходить к задаче с ростом серьезно разумеется и выборка нужна больше и проверка допущений теста, тут просто для пример привел эту задачу.
0
А по какому закону распределен рост человека? В медикобиологических исследованиях часто по умолчанию подразумевают нормальное распределение (я не утверждаю, что это правильно). Даже тот же же Гланц любит приводить примеры с ростом.
Другой аспект связан с тем, что на практике t-критерий весьма робастен, и его все же используют даже со слегка асимметричными распределениями.
Другой аспект связан с тем, что на практике t-критерий весьма робастен, и его все же используют даже со слегка асимметричными распределениями.
0
Подразумевать можно все, что угодно. Весь вопрос в том, можем ли мы предъявить вероятность нашей ошибки (и ошибочных выводов) при подобного рода заблуждениях. Если можем, то все хорошо, если нет… то вылезают всевозможного рода эффекты.
t-критерий как раз очень сильно «неробастен». При маленьких объемах выборки и толстых хвостах / несимметричных распределениях распределение нулевой гипотезы может очень сильно отличаться от распределения Стьюдента. Ну и говорить о «робастности» применительно к критерию с простой гипотезой как-то вообще странно. Он был бы «робастным», если бы сохранял вероятность ошибки первого рода при отклонении распределения от нормального. А это не так. Применения на практике обычно обосновываются тем, что «ну давайте получим доверительные интервалы пошире», естественно сильно проигрывая в мощности за счет занижения вероятности ошибки первого рода критерия.
Все начинает быть не так грустно, когда объем выборки становится сколько-нибудь нетривиальным (say, n > 50), и тогда в силу ЦПТ критерий становится асимптотическим (возможно, именно это Анатолий и имел в виду под неизвестным мне «z-распределением» выше, которое там на самом деле стандартное нормально).
И как бы на самом деле нас не интересует распределение роста. Нас интересует гипотеза относительно значения среднего. Зачем нам тогда точный критерий с дополнительными (сильными) предположениями? Может быть лучше рассмотреть выборку побольше, взять асимптотический критерий и получить то, что надо. Если же у нас только 10 человек, то надо правильно выбирать инструмент — можно, например, попробовать непараметрические тесты (правда, тогда гипотеза будет о медиане) или же воспользоваться перестановочным критерием и вычислить распределение статистики критерия явно.
t-критерий как раз очень сильно «неробастен». При маленьких объемах выборки и толстых хвостах / несимметричных распределениях распределение нулевой гипотезы может очень сильно отличаться от распределения Стьюдента. Ну и говорить о «робастности» применительно к критерию с простой гипотезой как-то вообще странно. Он был бы «робастным», если бы сохранял вероятность ошибки первого рода при отклонении распределения от нормального. А это не так. Применения на практике обычно обосновываются тем, что «ну давайте получим доверительные интервалы пошире», естественно сильно проигрывая в мощности за счет занижения вероятности ошибки первого рода критерия.
Все начинает быть не так грустно, когда объем выборки становится сколько-нибудь нетривиальным (say, n > 50), и тогда в силу ЦПТ критерий становится асимптотическим (возможно, именно это Анатолий и имел в виду под неизвестным мне «z-распределением» выше, которое там на самом деле стандартное нормально).
И как бы на самом деле нас не интересует распределение роста. Нас интересует гипотеза относительно значения среднего. Зачем нам тогда точный критерий с дополнительными (сильными) предположениями? Может быть лучше рассмотреть выборку побольше, взять асимптотический критерий и получить то, что надо. Если же у нас только 10 человек, то надо правильно выбирать инструмент — можно, например, попробовать непараметрические тесты (правда, тогда гипотеза будет о медиане) или же воспользоваться перестановочным критерием и вычислить распределение статистики критерия явно.
0
Некоторое время назад на реддите встретил такое обяснение почему n-1
"In statistical terms the degrees of freedom relate to the number of observations that are free to vary. If we take a sample of four observations from a population, then these four scores are free to vary in any way (they can be any value). However, if we then use this sample of four observations to calculate the mean squared error in the population, we have to use the mean of the sample as an estimate of the populations mean. Thus we hold one parameter constant. Say that the mean of the sample was 10; then we assume that the population mean is 10 also and we keep this value constant. With this parameter fixed, can all four score from our sample vary? The answer is no, because to ensure that the population mean is 10 only three values are free to vary. For example, if the values in the sample were 8, 9, 11, 12 (mean = 10) and we changed three of these values to 7, 15, and 8, then the final value must be 10 so that the mean is also 10. Therefore, if we hold one parameter constant then the degrees of freedom must be one less than the number of scores used to calculate that parameter. This fact explains why when we use a sample to estimate the mean squared error (or indeed the standard deviation) of a population, we divide the sums of squares by N — 1 rather than N alone" --Andy Field, Discovering Statistics Using IBM SPSS Statistics
0
This fact explains why when we use a sample to estimate the mean squared error (or indeed the standard deviation) of a population, we divide the sums of squares by N — 1 rather than N alone" --Andy Field, Discovering Statistics Using IBM SPSS Statistics
Это довольно странно, N — 1 в выборочном стандартном отклонении возникает в результате нашей борьбы со смещенностью.
Это довольно странно, N — 1 в выборочном стандартном отклонении возникает в результате нашей борьбы со смещенностью.
0
Если мы не применяем байесовский подход
А будет пост о том как применять этот подход? А то я как-то искал, но ничего не нашёл, есть описание как применять теорему Байеса, но оно не про тестирование гипотез т.к. нужно знать реальную вероятность, можно предположить, что это какой-то итеративный процесс, может быть с бинарным поиском, но хотелось бы внятного объяснения от специалистов.
0
Честно говоря пока не получает уложить в голове все эти объяснения, вот тут ответ от юзера sevenkul мне кажется близким к тому каким должно быть инутуитивное объяснение, хотя и там есть «One can prove easily.» которое стоилом бы пояснить.
Если кто-то сможет пояснить, добавить про то, что с ростом n влияние вычитания единицы снижается, то получится неплохое доступное для всех объяснение.
Если кто-то сможет пояснить, добавить про то, что с ростом n влияние вычитания единицы снижается, то получится неплохое доступное для всех объяснение.
0
Нихрена не понятно объяснили!
Степень свободы это число наблюдений минус 1 (пример с игральной костью: подкинули ее 100 раз, число степеней свободы 100-1)
ИЛИ
это число всевозможных вариантов наблюдений минус 1 (пример с игральной костью: 6 граней, то есть число степеней свободы 6 — 1)
?
Степень свободы это число наблюдений минус 1 (пример с игральной костью: подкинули ее 100 раз, число степеней свободы 100-1)
ИЛИ
это число всевозможных вариантов наблюдений минус 1 (пример с игральной костью: 6 граней, то есть число степеней свободы 6 — 1)
?
0
Sign up to leave a comment.
О степенях свободы в статистике