В этой части мы не будем говорить о рекомендательных системах как таковых. Вместо этого мы отдельно сконцентрируемся на главном инструменте машинного обучения — теореме Байеса — и рассмотрим один простой пример её применения — наивный байесовский классификатор. Disclaimer: знакомому с предметом читателю я вряд ли тут сообщу что-то новое, поговорим в основном о базовой философии машинного обучения.
Теорему Байеса или помнит, или тривиально может вывести любой, кто проходил хоть самый-самый базовый курс теории вероятностей. Помните, что такое условная вероятность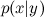
события x при условии события y? Прямо по определению: 
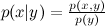, где 
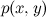– это совместная вероятность x и y, а p(x) и p(y) – вероятности каждого события по отдельности. Значит, совместную вероятность можно выразить двумя способами:
.
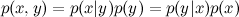Ну, вот вам и теорема Байеса:
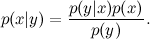
Вы, наверное, думаете, что я над вами издеваюсь — как может тривиально-тавтологичное переписывание определения условной вероятности быть основным инструментом чего бы то ни было, тем более такой большой и нетривиальной науки, как машинное обучение? Однако давайте начнём разбираться; сначала просто перепишем теорему Байеса в других обозначениях (да-да, я продолжаю издеваться):
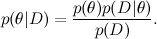
А теперь давайте соотнесём это с типичной задачей машинного обучения. Здесь D — это данные, то, что мы знаем, а θ — это параметры модели, которые мы хотим обучить. Например, в модели SVD данные — это те рейтинги, которые ставили пользователи продуктам, а параметры модели — факторы, которые мы обучаем для пользователей и продуктов.
Каждая из вероятностей тоже имеет свой смысл.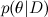
— это то, что мы хотим найти, распределение вероятностей параметров модели после того, как мы приняли во внимание данные; это называется апостериорной вероятностью (posterior probability). Эту вероятность, как правило, напрямую не найти, и здесь как раз и нужна теорема Байеса. 
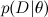– это так называемое правдоподобие (likelihood), вероятность данных при условии зафиксированных параметров модели; это как раз найти обычно легко, собственно, конструкция модели обычно в том и состоит, чтобы задать функцию правдоподобия. А 
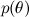— априорная вероятность (prior probability), она является математической формализацией нашей интуиции о предмете, формализацией того, что мы знали раньше, ещё до всяких экспериментов.
Здесь, наверное, не время и не место в это углубляться, но заслуга преподобного Томаса Байеса была, конечно, не в том, чтобы переписать в две строчки определение условной вероятности (не было тогда таких определений), а как раз в том, чтобы выдвинуть и развить такой взгляд на само понятие вероятности. Сегодня «байесовским подходом» называют рассмотрение вероятностей с позиций скорее «степеней доверия», чем фриквентистской (от слова frequency, а не freak!) «доли успешных экспериментов при стремлении к бесконечности общего числа экспериментов». В частности, это позволяет рассуждать о вероятностях одноразовых событий – ведь на самом деле нет никакого «стремящегося к бесконечности числа экспериментов» для событий вроде «Россия станет чемпионом мира по футболу в 2018 году» или, ближе к нашей теме, «Васе понравится фильм «Трактористы»»; тут скорее как с динозавром: или понравится, или нет. Ну а математика, конечно, при этом везде одна и та же, колмогоровским аксиомам вероятности всё равно, что о них думают.
Для закрепления пройденного — простой пример. Рассмотрим задачу категоризации текстов: например, предположим, что мы пытаемся рассортировать по темам поток новостей на основе уже имеющейся базы данных с темами: спорт, экономика, культура… Мы будем использовать так называемую bag-of-words model: представлять документ (мульти)множеством слов, которые в нём содержатся. В результате каждый тестовый пример x принимает значения из множества категорий V и описывается атрибутами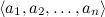
. Нам нужно найти наиболее вероятное значение данного атрибута, т.е.
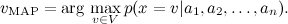
По теореме Байеса,
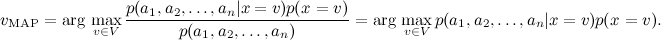
Оценить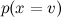
легко: будем просто оценивать частоту его встречаемости. Но оценить разные 
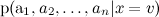не получится — их слишком много, 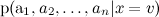— это вероятность в точности такого набора слов в сообщениях на разные темы. Очевидно, такой статистики взять неоткуда.
Чтобы с этим справиться, наивный байесовский классификатор (naive Bayes classifier — его иногда даже называют idiot’s Bayes) предполагает условную независимость атрибутов при условии данного значения целевой функции:
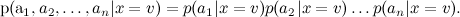
Теперь обучить отдельные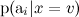
гораздо проще: достаточно подсчитать статистику встречаемости слов в категориях (там есть ещё одна деталь, которая приводит к двум разным вариантам наивного байеса, но мы сейчас углубляться в детали не будем).
Заметим, что наивный байесовский классификатор делает чертовски сильное предположение: в классификации текстов мы предполагаем, что разные слова в тексте на одну и ту же тему появляются независимо друг от друга. Это, конечно, полный бред — но, тем не менее, результаты получаются вполне приличные. На самом деле наивный байесовский классификатор гораздо лучше, чем кажется. Его оценки вероятностей оптимальны, конечно, только в случае настоящей независимости; но сам классификатор оптимален в куда более широком классе задач, и вот почему. Во-первых, атрибуты, конечно, зависимы, но их зависимость одинакова для разных классов и «взаимно сокращается» при оценке вероятностей. Грамматические и семантические зависимости между словами одни и те же и в тексте про футбол, и в тексте о байесовском обучении. Во-вторых, для оценки вероятностей наивный байес очень плох, но как классификатор гораздо лучше (обычно, если даже на самом деле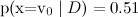
и 
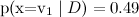, наивный байес выдаст 
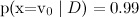и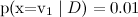 
, но классификация при этом будет чаще правильная).
В следующей серии мы усложним этот пример и рассмотрим модель LDA, которая способна выделять темы в корпусе документов безо всякого набора отмеченных документов, причём так, что один документ сможет содержать несколько тем, а также применим её к задаче рекомендаций.
Теорему Байеса или помнит, или тривиально может вывести любой, кто проходил хоть самый-самый базовый курс теории вероятностей. Помните, что такое условная вероятность
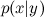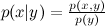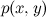события x при условии события y? Прямо по определению: , где – это совместная вероятность x и y, а p(x) и p(y) – вероятности каждого события по отдельности. Значит, совместную вероятность можно выразить двумя способами: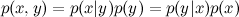.Ну, вот вам и теорема Байеса:
Вы, наверное, думаете, что я над вами издеваюсь — как может тривиально-тавтологичное переписывание определения условной вероятности быть основным инструментом чего бы то ни было, тем более такой большой и нетривиальной науки, как машинное обучение? Однако давайте начнём разбираться; сначала просто перепишем теорему Байеса в других обозначениях (да-да, я продолжаю издеваться):
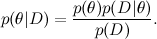
А теперь давайте соотнесём это с типичной задачей машинного обучения. Здесь D — это данные, то, что мы знаем, а θ — это параметры модели, которые мы хотим обучить. Например, в модели SVD данные — это те рейтинги, которые ставили пользователи продуктам, а параметры модели — факторы, которые мы обучаем для пользователей и продуктов.
Каждая из вероятностей тоже имеет свой смысл.
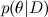— это то, что мы хотим найти, распределение вероятностей параметров модели после того, как мы приняли во внимание данные; это называется апостериорной вероятностью (posterior probability). Эту вероятность, как правило, напрямую не найти, и здесь как раз и нужна теорема Байеса. 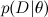– это так называемое правдоподобие (likelihood), вероятность данных при условии зафиксированных параметров модели; это как раз найти обычно легко, собственно, конструкция модели обычно в том и состоит, чтобы задать функцию правдоподобия. А 
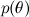— априорная вероятность (prior probability), она является математической формализацией нашей интуиции о предмете, формализацией того, что мы знали раньше, ещё до всяких экспериментов.Здесь, наверное, не время и не место в это углубляться, но заслуга преподобного Томаса Байеса была, конечно, не в том, чтобы переписать в две строчки определение условной вероятности (не было тогда таких определений), а как раз в том, чтобы выдвинуть и развить такой взгляд на само понятие вероятности. Сегодня «байесовским подходом» называют рассмотрение вероятностей с позиций скорее «степеней доверия», чем фриквентистской (от слова frequency, а не freak!) «доли успешных экспериментов при стремлении к бесконечности общего числа экспериментов». В частности, это позволяет рассуждать о вероятностях одноразовых событий – ведь на самом деле нет никакого «стремящегося к бесконечности числа экспериментов» для событий вроде «Россия станет чемпионом мира по футболу в 2018 году» или, ближе к нашей теме, «Васе понравится фильм «Трактористы»»; тут скорее как с динозавром: или понравится, или нет. Ну а математика, конечно, при этом везде одна и та же, колмогоровским аксиомам вероятности всё равно, что о них думают.
Для закрепления пройденного — простой пример. Рассмотрим задачу категоризации текстов: например, предположим, что мы пытаемся рассортировать по темам поток новостей на основе уже имеющейся базы данных с темами: спорт, экономика, культура… Мы будем использовать так называемую bag-of-words model: представлять документ (мульти)множеством слов, которые в нём содержатся. В результате каждый тестовый пример x принимает значения из множества категорий V и описывается атрибутами
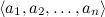. Нам нужно найти наиболее вероятное значение данного атрибута, т.е.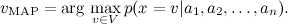
По теореме Байеса,
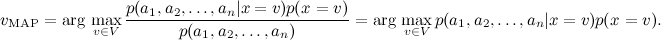
Оценить
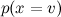легко: будем просто оценивать частоту его встречаемости. Но оценить разные 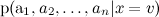не получится — их слишком много, 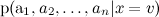— это вероятность в точности такого набора слов в сообщениях на разные темы. Очевидно, такой статистики взять неоткуда.Чтобы с этим справиться, наивный байесовский классификатор (naive Bayes classifier — его иногда даже называют idiot’s Bayes) предполагает условную независимость атрибутов при условии данного значения целевой функции:
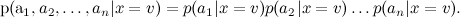
Теперь обучить отдельные
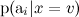гораздо проще: достаточно подсчитать статистику встречаемости слов в категориях (там есть ещё одна деталь, которая приводит к двум разным вариантам наивного байеса, но мы сейчас углубляться в детали не будем).Заметим, что наивный байесовский классификатор делает чертовски сильное предположение: в классификации текстов мы предполагаем, что разные слова в тексте на одну и ту же тему появляются независимо друг от друга. Это, конечно, полный бред — но, тем не менее, результаты получаются вполне приличные. На самом деле наивный байесовский классификатор гораздо лучше, чем кажется. Его оценки вероятностей оптимальны, конечно, только в случае настоящей независимости; но сам классификатор оптимален в куда более широком классе задач, и вот почему. Во-первых, атрибуты, конечно, зависимы, но их зависимость одинакова для разных классов и «взаимно сокращается» при оценке вероятностей. Грамматические и семантические зависимости между словами одни и те же и в тексте про футбол, и в тексте о байесовском обучении. Во-вторых, для оценки вероятностей наивный байес очень плох, но как классификатор гораздо лучше (обычно, если даже на самом деле
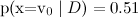и 
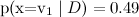, наивный байес выдаст 
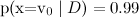и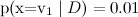 
, но классификация при этом будет чаще правильная).В следующей серии мы усложним этот пример и рассмотрим модель LDA, которая способна выделять темы в корпусе документов безо всякого набора отмеченных документов, причём так, что один документ сможет содержать несколько тем, а также применим её к задаче рекомендаций.
