How to become an author
Search
Write a publication
Pull to refresh
1986.89
Rating
Timeweb Cloud
То самое облако

JavaScript: заметка о побитовых операторах и числах с плавающей точкой

Reading time9 min
Views10K
Timeweb Cloud corporate blogJavaScript*


Привет, друзья!


В этой небольшой заметке я хочу поговорить с вами о манипулировании битами в JavaScript, а также о двоичном представлении чисел с плавающей точкой (floating point numbers).


Обратите внимание: заметка носит, в основном, теоретический характер и направлена на углубленное изучение JavaScript, поэтому предполагается, что вы имеете некоторый опыт работы с данным языком программирования.


С вашего позволения, я не буду рассказывать о двоичной системе счисления и побитовых операторах. О последних хорошо написано здесь.


Начнем с определения функции для вывода в консоль инструментов разработчика в браузере переданного числа в бинарном формате (для типизации параметров и возвращаемого значения я прибегну к помощи TypeScript):


// https://stackoverflow.com/questions/9939760/how-do-i-convert-an-integer-to-binary-in-javascript
const log = (n: number): void => {
  console.log((n >>> 0).toString(2))
}

Рассмотрим несколько примеров из этого репозитория.


Функция получения бита


const getBit = (n: number, bitPosition/* начиная с 0 */: number): number => (n >> bitPosition) & 1

console.log(getBit(2, 1)) // 1

Сначала мы сдвигаем соответствующий бит в нулевую позицию. Затем выполняем операцию & с 1, которая выглядит как 0001 в двоичном представлении. Это приводит к удалению из числа всех битов, кроме искомого. Если оставшийся бит является 1, возвращается 1, иначе возвращается 0.


Функция установки бита


const setBit = (n: number, bitPosition: number): number => n | (1 << bitPosition)

log(2)            // 10
log(setBit(2, 0)) // 11

Сначала мы сдвигаем 1 на количество битов, указанных в bitPosition, создавая значение, похожее на 0010. Затем выполняем операцию |, которая устанавливает соответствующий бит в значение 1, но не влияет на другие биты числа.


Функция очистки бита


function clearBit(n: number, bitPosition: number): number {
  const mask = ~(1 << bitPosition)

  return n & mask
}

log(5)              // 101
log(clearBit(5, 0)) // 100

Сначала мы сдвигаем 1 на количество битов, указанных в bitPosition, создавая значение, похожее на 0010. Затем инвертируем это значение (обращаем биты на противоположные), получая что-то вроде 1101. После этого выполняем операцию & над обоими значениями. Это приводит к удалению соответствующего бита.


Функция обновления бита


function updateBit(n: number, bitPosition: number, bitValue/* 0 или 1 */: number): number {
  const normalized = bitValue ? 1 : 0
  const mask = ~(1 << bitPosition)
  return (n & mask) | (normalized << bitPosition)
}

Это просто сочетание методов clearBit и setBit.


Функция определения четности числа


const isEven = (n: number): number => (n & 1) === 0

// 100
console.log(isEven(4)) // true
// 101
console.log(isEven(5)) // false

// или
const isOddOrEven = (n: number): string => (n & 1 ? 'нечетное' : 'четное')
console.log(isOddOrEven(4)) // четное
console.log(isOddOrEven(5)) // нечетное

Здесь весь фокус состоит в том, что крайним правым битом нечетного числа всегда является 1.


Функция определения положительности числа


function isPositive(n: number): number {
  if (n === 0) return false

  return ((n >> 31) & 1) === 0
}

console.log(isPositive(1))  // true
console.log(isPositive(0))  // false
console.log(isPositive(-1)) // false

Крайним левым (старшим) битом положительного числа всегда является 0. При этом, для +0 (или просто 0) и -0 должно возвращаться false.


Функция умножения числа на 2


const multiplyByTwo = (n: number): number => n << 1

log(5)                        // 0101 -> 0 + 2^2 + 0 + 2^0 (см. ниже)
log(multiplyByTwo(5))         // 1010 -> 2^3 + 0 + 2^1 + 0
console.log(multiplyByTwo(5)) // 10

Мы сдвигаем все биты числа влево по одному. Это приводит к тому, что все компоненты бинарного числа (степени числа 2) умножаются на 2, поэтому и само число также умножается на 2.


Функция деления числа на 2


const divideByTwo = (n: number): number => n >> 1

log(4)                      // 100 -> 2^2 + 0 + 0
log(divideByTwo(4))         // 010 -> 0 + 0 + 2^1
console.log(divideByTwo(4)) // 2

Мы сдвигаем все биты числа вправо по одному. Это приводит к тому, что все компоненты бинарного числа (степени числа 2) делятся на 2, поэтому и само число также делится на 2.


Функция смены знака числа


const switchSign = (n: number): number => ~n + 1

log(2)                     // 10
log(switchSign(2))         // -10
console.log(switchSign(2)) // -2

Мы инвертируем все биты числа и прибавляем к нему 1. Данная техника называется "дополнительным кодом" или "дополнением до двух" (two's complement).


Функция определения количества установленных битов


function countSetBits(n: number): number {
  let count = 0

  while (number) {
    // добавляем последний бит к результату
    count += number & 1

    // сдвигаем число на 1 бит вправо для достижения других битов
    number >>>= 1
  }

  return count
}

log(5)                        // 101
console.log(countSetBits(5))  // 2

Основная идея здесь состоит в том, что число сдвигается вправо по одному биту. Результат операции & возвращает либо 1, либо 0.


Функция определения количества битов


function countBits(n: number): number {
  let count = 0

  while (1 << count <= n) {
    count += 1
  }

  return count
}

log(5)                    // 101
console.log(countBits(5)) // 3

Мы каждый раз сдвигаем 1 на один бит влево и проверяем, не стало ли "сдвинутое" число больше или равно переданному. В приведенном примере для того, чтобы сдвинутое число стало больше или равно 5, 1 необходимо сдвинуть 4 раза.


Функция определения того, является ли число степенью числа 2


const isPowerOfTwo = (n: number): number => (n & (n - 1)) === 0

console.log(isPowerOfTwo(4)) // true
console.log(isPowerOfTwo(5)) // false

Предположим, что n — это число, которое является степенью числа 2 (2, 4, 8, 16 и т.д.). Тогда операция &, примененная к n и n - 1, возвращает 0:


4 & (4 - 1) = 100 & 011 = 000 -> число является степенью числа 2
10 & (10 - 9) = 1010 & 1001 = 1000 -> число не является степенью числа 2

Функция умножения 2 чисел со знаками


/**
 * Если значением `a` или `b`, или обоих множителей является `0`:
 * multiplySigned(a, b) === 0
 *
 * Если `b` - четное число:
 * multiplySigned(a, b) === multiplySigned(2 * a, b / 2)
 *
 * Если `b` - нечетное положительное число:
 * multiplySigned(a, b) === multiplySigned(2 * a, (b - 1) / 2) + a
 *
 * Если `b` - нечетное отрицательное число:
 * multiplySigned(a, b) === multiplySigned(2 * a, (b + 1) / 2) - a
 *
 * Временная сложность: O(log b)
 */
function multiplySigned(a: number, b: number): number {
  if (b === 0 || a === 0) return 0

  const multiplyByOddPositive = () =>
    multiplySigned(multiplyByTwo(a), divideByTwo(b - 1)) + a
  const multiplyByOddNegative = () =>
    multiplySigned(multiplyByTwo(a), divideByTwo(b + 1)) - a

  const multiplyByEven = () => multiplySigned(multiplyByTwo(a), divideByTwo(b))
  const multiplyByOdd = () =>
    isPositive(b) ? multiplyByOddPositive() : multiplyByOddNegative()

  return isEven(b) ? multiplyByEven() : multiplyByOdd()
}

console.log(multiplySigned(2, -4)) // -8

Выражение a * b может быть представлено следующим образом:


  • 0: когда a или b, или a и b равны 0;
  • 2a * (b/2): когда b — это четное число;
  • 2a * (b-1)/2 + a: когда b — это четное положительное число;
  • 2a * (b+1)/2 - a: когда b — это четное отрицательное число.

Преимущество такого подхода состоит в том, что на каждом шаге рекурсии значение одного из операндов уменьшается вдвое. Мы имеем временную сложность O(log b), поскольку b — это операнд, значение которого уменьшается в 2 раза при каждом рекурсивном вызове функции.


Функция умножения 2 чисел без знаков


function multiplyUnsigned(x: number, y: number): number {
  let result = 0

  // пусть `y` будет множителем `x`
  let multiplier = y

  // текущий индекс бита множителя
  let bitIndex = 0

  // перебираем биты `y`
  while (multiplier !== 0) {
    // проверяем, установлен ли текущий бит
    if (multiplier & 1) {
      // если бит с текущим индексом установлен,
      // значит, нужно умножить `x` на степень этого бита
      // и добавить его к результату
      result += x << bitIndex
    }

    bitIndex += 1
    multiplier >>= 1
  }

  return result
}

console.log(multiplyUnsigned(2, 4)) // 8

В основе этого метода лежит идея о том, что любое число можно представить как сумму степеней числа 2:


19 = 2^4 + 2^1 + 2^0

Поэтому умножение числа x на 19 эквивалентно следующему:


x * 19 = x * 2^4 + x* 2^1 + x * 2^0

А x * 2^4 означает сдвиг x на 4 бита влево (x << 4).


Пожалуй, на этом мы закончим рассмотрение примеров использования побитовых операторов для манипулирования битами чисел.


Что касается практического применения этих операторов в JavaScript, то, кроме приведенных выше функций для определения четности и положительности числа, следует упомянуть о двойном операторе ~, который может использоваться как альтернатива методу Math.floor:


const n = ~~3.14
console.log(n) // 3

А также об одиночном операторе ~, с помощью которого можно выполнить проверку на -1:


const arr = [3, 1, 2]
arr.forEach((_, i) => {
  if (~arr.indexOf(i)) {
    console.log(`В массиве есть ${i}`)
  }
})
/**
 * В массиве есть 1
 * В массиве есть 2
 */

Как видите, случаев использования побитовых операторов в JavaScript на так уж и много.


На практике я также встречал побитовые операторы в следующих функциях:


  • функция для генерации UUID (Node.js):

const genUuid = () =>
  ([1e7] + -1e3 + -4e3 + -8e3 + -1e11).replace(/[018]/g, (c) =>
    (
      c ^
      (crypto.getRandomValues(new Uint8Array(1))[0] & (15 >> (c / 4)))
    ).toString(16)
  )

console.log(genUuid()) // 7982fcfe-5721-4632-bede-6000885be57d

  • функция для получения случайного цвета в формате HEX:

const getRandomHexColor = () =>
  `#${((Math.random() * 0xffffff) << 0).toString(16)}`

console.log(getRandomHexColor()) // #6ec80d

  • функция для преобразования цвета из RGB в HEX:

const RgbToHex = (r, g, b) =>
  `#${((r << 16) + (g << 8) + b).toString(16).padStart(6, '0')}`

console.log(RgbToHex(255, 200, 55)) // #ffc837

А какие примеры использования побитовых операторов знаете вы? Поделитесь в комментариях.


Теперь поговорим о двоичном представлении чисел с плавающей точкой.


Числа двойной точности в бинарном формате


Источник.


Вы когда-нибудь задумывались о том, как компьютеры хранят числа с плавающей точкой, такие как 3.1416 (число Пи) или 9.109 × 10⁻³¹ (масса электрона в кг), в памяти, ограниченной определенным количеством нулей и единиц (битов)?


В случае с целыми числами (например, числом 17) все достаточно просто. Допустим, у нас есть 16 бит (2 байта) для хранения числа. В 16 битах можно хранить числа в диапазоне [0, 65535]:


(0000000000000000)₂ = (0)₁₀

(0000000000010001)₂ =
    (1 × 2⁴) +
    (0 × 2³) +
    (0 × 2²) +
    (0 × 2¹) +
    (1 × 2⁰) = (17)₁₀

(1111111111111111)₂ =
    (1 × 2¹⁵) +
    (1 × 2¹⁴) +
    (1 × 2¹³) +
    (1 × 2¹²) +
    (1 × 2¹¹) +
    (1 × 2¹⁰) +
    (1 × 2⁹) +
    (1 × 2⁸) +
    (1 × 2⁷) +
    (1 × 2⁶) +
    (1 × 2⁵) +
    (1 × 2⁴) +
    (1 × 2³) +
    (1 × 2²) +
    (1 × 2¹) +
    (1 × 2⁰) = (65535)₁₀

Если требуется хранить число со знаком, можно использовать дополнение до двух и сдвинуть диапазон [0, 65535] в отрицательную сторону. В этом случае 16 бит будут представлять числа в диапазоне [-32768, +32768].


Как можно заметить, такой подход не позволяет хранить числа наподобие -27.15625 (числа после точки будут игнорироваться).


Конечно, мы далеко не первые, кто заметил эту проблему. В далеком 1985 году умные люди преодолели это ограничение, представив стандарт IEEE 754 для чисел с плавающей точкой (далее — стандарт).


Стандарт описывает способ использования 16 бит (или 32, или 64) для хранения чисел более широкого диапазона, включая маленькие числа от 0 до 1.


Для того, чтобы понять идею, лежащую в основе стандарта, следует прибегнуть к экспоненциальной записи (scientific notation) — способу представления чисел, которые являются слишком большими или слишком маленькими (обычно, представленными в виде длинной строки из чисел) для того, чтобы быть пригодными для записи в десятичной форме.





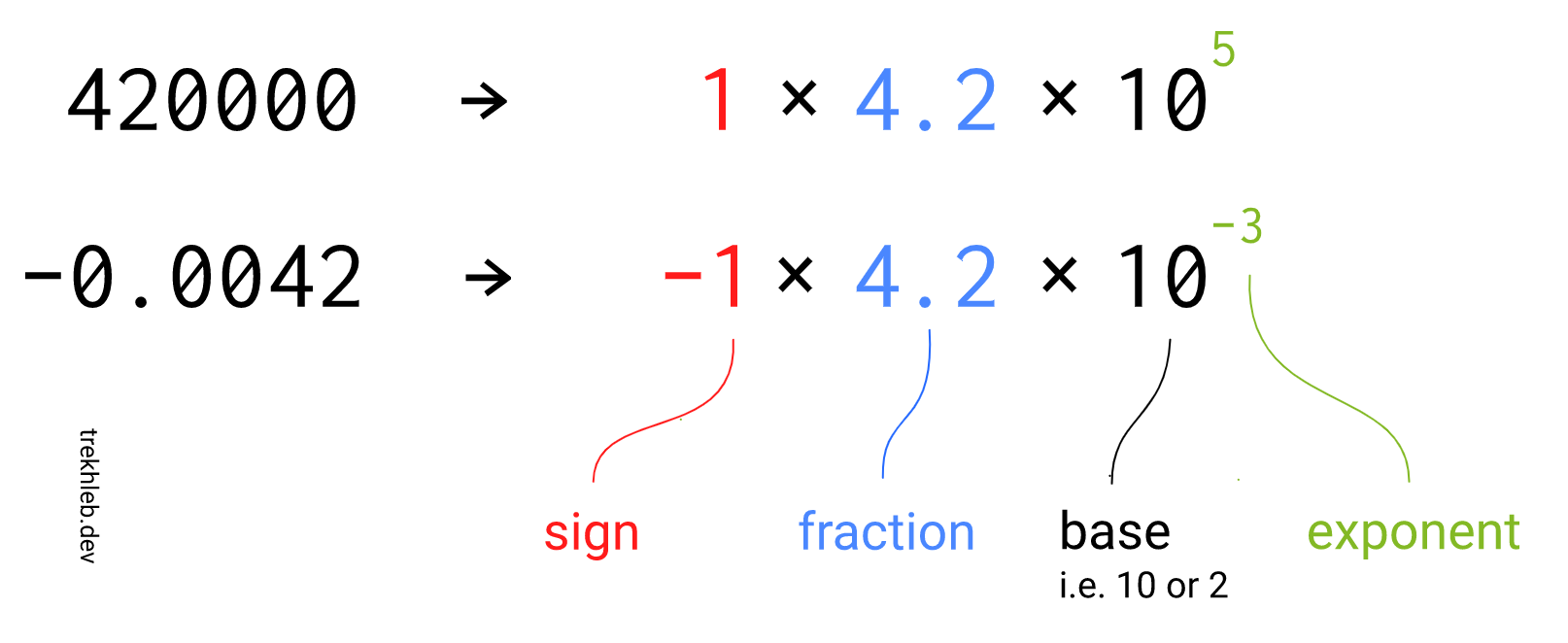
Как видно на изображении, представление числа может быть разделено на 3 части:


  • sign — знак;
  • fraction (significand) — фракция (значимые числа, полезная нагрузка) числа;
  • exponent — экспонента, определяющая, как далеко и в каком направлении сдвигается точка во фракции.

Часть base (основа, система счисления) можно опустить, условившись о том, чему она будет равняться. Мы в качестве основы будет использовать 2.


Вместо использования всех 16 бит (или 32, или 64) для хранения фракции числа, биты могут быть разделены для хранения знака, экспоненты и фракции по-отдельности. В зависимости от количества битов, имеющихся в нашем распоряжении для хранения числа, получается следующая таблица:


Формат Общее количество битов Количество битов для знака Для экспоненты Для фракции Основа
Половинная точность 16 1 5 10 2
Одинарная точность 32 1 8 23 2
Двойная точность 64 1 11 52 2

При таком подходе мы получаем меньшее количество битов для фракции (например, вместо 16 получаем всего 10). Это означает, что во фракцию можно записать меньший диапазон чисел (с незначительной потерей точности). Однако, поскольку у нас также имеется часть для экспоненты, на самом деле диапазон чисел расширяется. Это также позволяет описывать числа между 0 и 1 (за счет отрицательной экспоненты).


Например, максимальный значением переменной для 32-битного целого числа является 2³¹ − 1 = 2,147,483,647, а максимальным значением переменной для 32-битных чисел с плавающей точкой с основанием 2 по стандарту является ≈ 3.4028235 × 10³⁸.


Для представления отрицательной экспоненты в стандарте используется смещение экспоненты (exponent bias) — вычитание смещения (bias) из экспоненты. Например, если экспонента имеет 5 бит, она может принимать значения в диапазоне [0, 31] (в данном случае все значения положительные). Но если мы вычтем из нее 15, то диапазон будет выглядеть как [-15, 16]. Число 15 называется смещением и рассчитывается по следующей формуле:


exponent_bias = 2 ^ (k − 1) − 1

k - количество битов экспоненты

На представленном ниже изображении описывается логика преобразования чисел с плавающей точкой в бинарном формате в десятичный формат. Для простоты используется 16-битное число, но точно такой же подход применяется в отношении 32 и 64-битных чисел:





В этой статье можно найти интерактивную версию приведенного изображения.


В следующей таблице представлены диапазоны, поддерживаемые разными форматами:


Формат Минимальная экспонента Максимальная экспонента Диапазон Минимальное положительное число
Половинная точность -14 +15 ±65,504 6.10 × 10⁻⁵
Одинарная точность -126 +127 ±3.4028235 × 10³⁸ 1.18 × 10⁻³⁸

Обратите внимание: в данной заметке представлен лишь краткий обзор стандарта. Существует несколько крайних случаев, которые обрабатываются в особом порядке. Речь идет о таких значениях, как -0, -Infinity, +Infinity и NaN.


Примеры кода


  • bitsToFloat — функция для преобразования массива битов в число с плавающей точкой;
  • floatAsBinaryString — функция для преобразования числа с плавающей точкой в двоичное представление согласно стандарту.

Полезные ссылки



Пожалуй, это все, чем я хотел поделиться с вами в данной заметке. Надеюсь, вы нашли для себя что-то интересное и не зря потратили время.


Благодарю за внимание и happy coding!



Tags:
Hubs:
Total votes 21: ↑21 and ↓0+21
Comments5
Timeweb Cloud
То самое облако
285
Karma
60.2
Rating
Igor Agapov @aio350

JavaScript Developer

Send message

Articles

Information

Website
timeweb.cloud
Registered
Founded
Employees
201–500 employees
Location
Россия
Representative
Timeweb Cloud

Your account

Sections

Information

Services

Support
© 2006–2024, Habr