
Скачать перевод в виде документа Mathematica, который содержит весь код использованный в статье, можно здесь (архив, ~5 МБ).
Введение
В русском языке, как и во многих других языках, существуют слова, которые имеют одинаковую длину, но при этом отличаются всего лишь одной буквой. Такого рода пары слов называются метаграммами.
Предположим, что у нас есть несколько последовательных метаграмм, скажем:
мнение-мление-тление-трение-прение-поение-роение-рдение-бдение-биение
они образуют цепь метаграмм, или цепочку слов.
Отсюда проистекает игра под названием цепь слов (word ladder), которую придумал в далеком 1879 году Льюис Кэрролл.
Ясно, что далеко не для каждого начального слова может быть составлена такого рода цепь, а некоторые слова, по-видимому, должны порождать довольно длинные цепи.
В этом посте мы постараемся проанализировать цепочки слов, которые могут быть построены в русском языке, а также найдем цепочки наибольшей длины.
Импорт списка слов русского языка
Для построения и анализа цепочек слов нам потребуется список слов, которые мы можем встретить в русском языке. В данном посте мы не будем делать ограничение на часть речи, которая может быть использована, но при этом будем рассматривать только форму слова, соответствующую именительному падежу в парадигме слова. Мы используем, как и в одном из предыдущих постов (Поиск наилучшей последовательности просмотра списка 250 лучших фильмов с помощью языка Wolfram Language (Mathematica)), морфологический словарь русского языка, созданный академиком Андреем Анатольевичем Зализняком:
In[1]:=
In[3]:=

Обработаем данные словаря, составив на его основе список слов русского языка russianWords:
In[4]:=

Функция, определяющая звено цепочки слов
Создадим функцию chainLinkQ, которая будут определять, могут ли два слова быть звеном цепочки слов, другими словами, эта функция отвечает на вопрос — являются ли два слова метаграммой.
При этом рассмотрим два варианта:
- слова отличаются одной буквой (в данном случае достаточно воспользоваться для проверки функцией EditDistance, которая вычисляет расстояние Левенштейна, результат вычисления которой должен равняться 1):
In[5]:=
- слова отличаются n соседними буквами:
In[6]:=

Функция поиска всех метаграмм слов фиксированной длины
Теперь найдем все звенья цепочек слов (метаграммы).
Для начала, разобьем все слова русского языка в классы эквивалентности, т. е., по сути мы построим фактор-множество слов русского языка по их длине, другими словами, разобьем список всех слов на множества слов из 1-й, 2-х, 3-х, 4-х и т. д. букв.
In[7]:=
Найдем минимальную и максимальную длину слова в русском языке:
In[8]:=
Out[8]=
Посмотрим на распределение слов русского языка по длине:
In[9]:=

Out[9]=
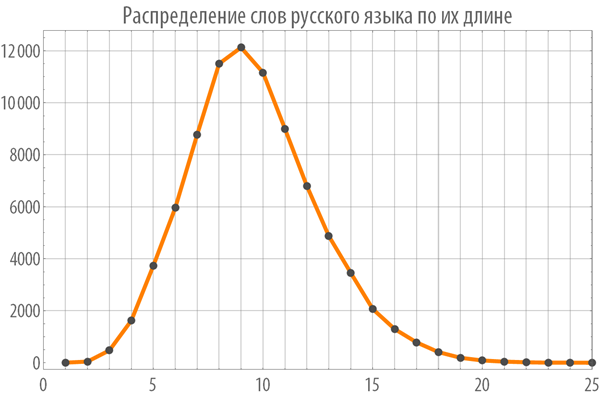
Теперь создадим функцию, сохраняющую свои вычисленные значения, которая будет отбирать среди всех возможных пар слов заданной длины те, которые могут быть звеньями цепочек слов:
In[10]:=

Вычислим эту функцию для каждого класса эквивалентности слов русского языка, при этом мы будет сейчас рассматривать только слова, отличающиеся на одну букву:
In[11]:=
Пример результата вычислений:
In[12]:=
Out[12]=

Графы цепочек слов
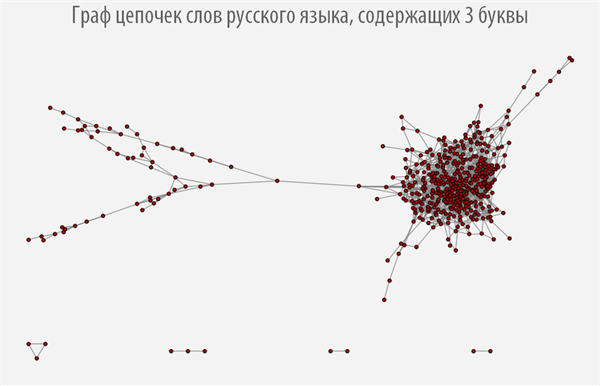
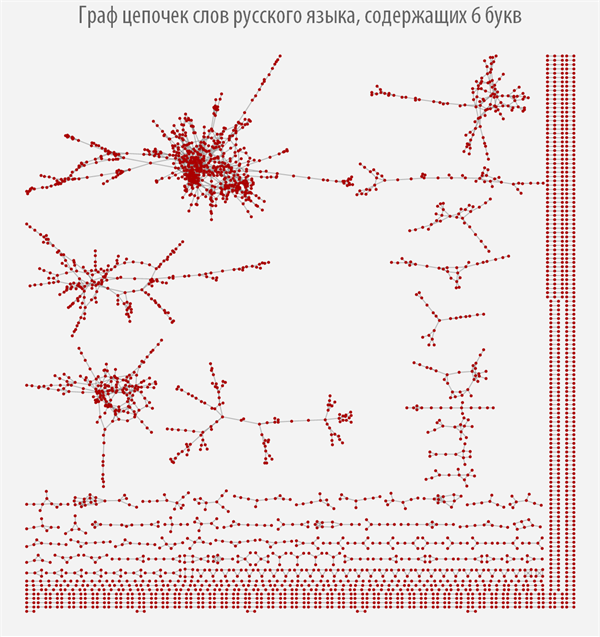
После того, как мы вычислили функцию поиска всех звеньев цепочек слов для каждого класса эквивалентности, мы можем построить соответствующие им графы, которые позволят наглядно изучить устройство цепочек слов каждого типа (если граф отсутствует, значит для слов данной длины нет ни одного звена).
При наведении на каждую из вершин графа вы можете получить всплывающую подсказку со словом, которому соответствует данная вершина графа (скачать документ с интерактивными графами и исходным кодом вы можете по ссылке, приведенной в самом начале поста).

In[13]:=

In[14]:=

Граф цепочек слов русского языка, содержащих 1 букву

Граф цепочек слов русского языка, содержащих 2 буквы




Граф цепочек слов русского языка, содержащих 8 букв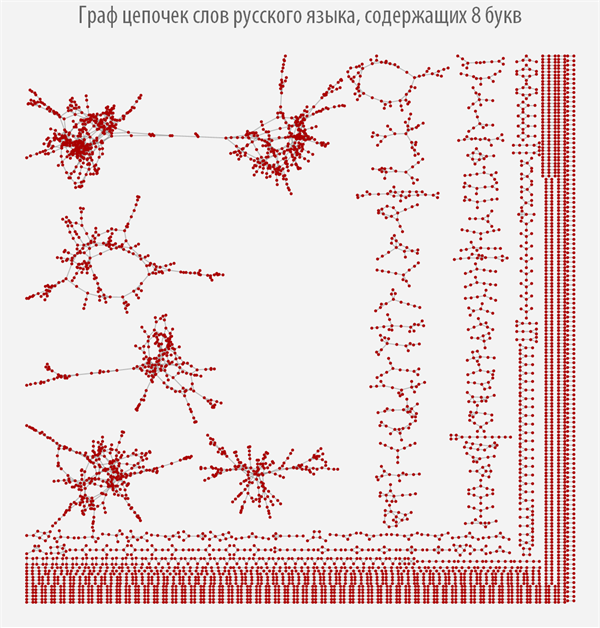

Граф цепочек слов русского языка, содержащих 9 букв

Граф цепочек слов русского языка, содержащих 10 букв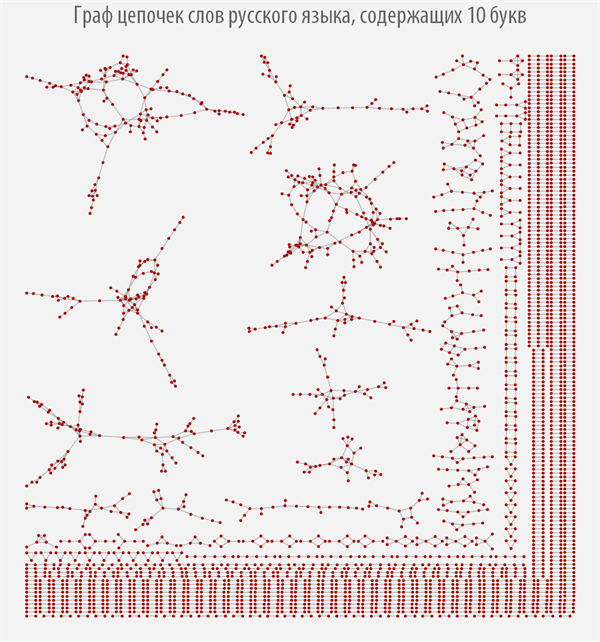

Граф цепочек слов русского языка, содержащих 11 букв

Граф цепочек слов русского языка, содержащих 12 букв

Граф цепочек слов русского языка, содержащих 13 букв

Граф цепочек слов русского языка, содержащих 14 букв

Граф цепочек слов русского языка, содержащих 15 букв

Граф цепочек слов русского языка, содержащих 16 букв

Граф цепочек слов русского языка, содержащих 17 букв

Граф цепочек слов русского языка, содержащих 18 букв

Граф цепочек слов русского языка, содержащих 21 букву

Из графов выше видно, как сильно меняется их структура в зависимости от длины слов, из которых он строится, при этом можно наблюдать, что большинство графов имеют более одной компоненты связности.
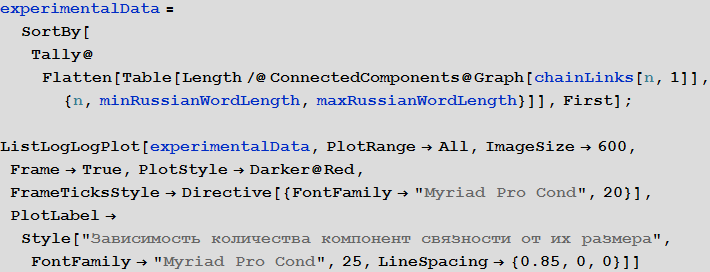
Из графика, представленного ниже можно видеть зависимость количества компонент связности различной длины среди всех рассмотренных выше графов, из которого следует, что зависимость должна иметь вид
In[15]:=
Out[16]=
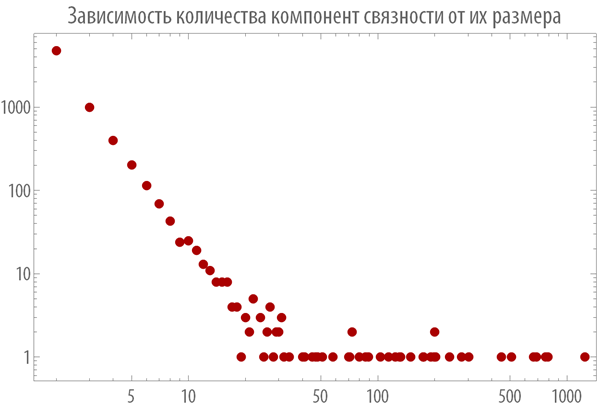
Действительно:
In[17]:=

Out[17]=
In[19]:=

Out[19]=

Предположение Дональда Кнута применительно к цепочкам слов в русском языке
Дональд Кнут одним из первых применил компьютер для исследования цепочек английского языка. Он изучал цепочки слов, состоящих из 5 букв, так как полагал, что слова из меньшего числа букв, скажем, 3-х слишком просты для изучения (хотя Льюис Кэрролл составил цепочку из 6 звеньев от слова APE до слова MAN), а слова из большего числа букв не смогут привести к длинным цепочкам, в том числе и потому, что соответствующий граф имеет много компонент связности.
Проверим предположение Кнута для цепочек слов русского языка.
График, представленный ниже, показывает то, как с увеличением числа букв в словах, из которых строятся цепочки меняется положение точки с координатами:
{количество компонент связности графа, количество рёбер графа}.
Верхний левый угол соответствует “идеальному графу” у которого одна компонента связности, при этом у него максимальное число рёбер. Граф, соответствующий наиболее близкой точке рассматриваемой траектории к данной точке, очевидно, может рассматриваться как “наилучший”. Соответствующая точка, найденная автоматически, помечена двумя красными окружностями и соответствует графу цепочек пятибуквенных слов.
Таким образом, можно утверждать, что предположение Дональда Кнута, сделанное для цепочек слов английского языка, так же, как это не удивительно, верно и для русского языка. Возможно в этом лежат довольно глубинные свойства человеческой психологии, завязанные на числа 5 и 10, соответствующие пальцам на одной и двух ладонях, соответственно.
In[20]:=

Out[25]=

Поиск самой длинной цепочки слов в русском языке
Итак, пройдя довольно долгий путь, мы наконец готовы найти самую длинную цепочку слов, которая существует в русском языке. Как следует из предыдущего раздела, она должна быть среди цепочек слов из пяти букв.
In[26]:=

Out[26]=

Итак, мы получили две самые длинные цепочки слов в русском языке, при этом, как и ожидалось, они содержатся в “наилучшем” графе цепочек пятибуквенных слов.
Поиск самых длинных цепочек n-буквенных слов русского языка
В предыдущем разделе мы искали самую длинную цепочку слов русского языка, и нами были найдены две цепочки из 40 пятибуквенных слов.
Давайте теперь посмотрим на самые длинные возможные цепочки n-буквенных слов:
In[27]:=

Цепочки слов русского языка, содержащих 2 буквы, с количеством слов не менее 5

Цепочки слов русского языка, содержащих 3 буквы, с количеством слов не менее 5




Цепочки слов русского языка, содержащих 7 букв, с количеством слов не менее 5

Цепочки слов русского языка, содержащих 8 букв, с количеством слов не менее 5

Цепочки слов русского языка, содержащих 9 букв, с количеством слов не менее 5

Цепочки слов русского языка, содержащих 10 букв, с количеством слов не менее 5

Цепочки слов русского языка, содержащих 11 букв, с количеством слов не менее 5

Цепочки слов русского языка, содержащих 12 букв, с количеством слов не менее 5

Цепочки слов русского языка, содержащих 13 букв, с количеством слов не менее 5

Заключение
Надеюсь, что мой пост смог заинтересовать вас, а некоторые идеи и программы, представленные в нем окажутся вам полезны. Безусловно, можно придумать еще массу интересных исследований русского языка. Скажем, в начале поста была создана функция chainLinkQ, функционал которой позволяет произвести аналогичное исследование для метаграмм, отличающихся двумя буквами — что соответствует, по сути, небольшой модификации правил игры в цепочки слов. Из двух графов, представленных ниже, видно, что граф четырёхбуквенных метаграмм, отличающихся двумя буквами является связным, по сравнению с графом метаграмм, отличающихся только лишь одной буквой. Это говорит о том, что результаты исследования таких графов и цепочек будут совершенно иными.
In[28]:=
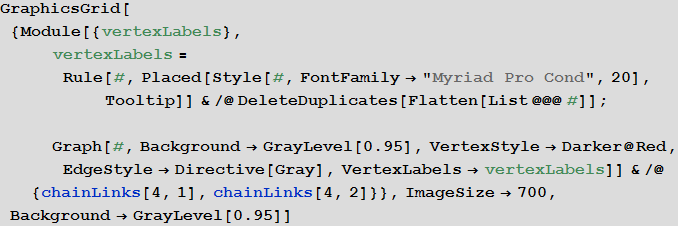
Out[28]=

Ресурсы для изучения Wolfram Language (Mathematica) на русском языке: http://habrahabr.ru/post/244451