Разбор задач финала чемпионата мира про программированию ACM ICPC 2013

На прошедшем неделю назад чемпионате мира по командному программированию ACM ICPC 2013 было 11 задач, одну из которых за отведённое время не смогла решить правильно ни одна из команд.

Но кроме команд есть и другие люди, которые профессионально решают задачи, — аналитики чемпионата. В течение трансляции они разбиваются на группы, распределяют задачи и потом рассказывают о них в студии. Множество зрителей следят за эфиром, пока эти ребята не разберут самую последнюю задачу. Кроме того, аналитики подсказывают ведущему, что происходит «на поле», высматривают интересные куски кода, следят за картинкой с веб-камер участников.

В этом году на ACM ICPC был 21 аналитик из Швеции, Нидерландов, США, Словакии, Беларуси и России. И 10 из них были из Яндекса. Все они в разные годы были призёрами ICPC. Специально для Хабра они разобрали все задания чемпионата.

Задача A. Self-Assembly

Одно высоконаучное химическое учреждение активно экспериментирует с Автоматическим Сборщиком Молекул. Молекулы, между которыми возможно образование химических связей, перемешивают и помещают в АСМ, где они образуют сложные молекулярные структуры. Однако иногда возникает проблема — молекулы образуют такую большую группу, что Сборщик заедает.

Напишите программу, которая будет определять, может ли предоставленный набор молекул собираться в структуры неограниченного размера. При этом 1) задача ограничена плоскими структурами и 2) каждая молекула имеет вид квадрата, все молекулы имеют одинаковый размер. Четыре стороны квадрата обозначают поверхности, которыми молекулы могут соединяться с совместимыми молекулами.

В каждом тесте вам будет представлен набор описаний молекул. Каждый тип молекулы описывается четырьмя парами символов — метками связей,
которые обозначают возможность соответствующей поверхности молекулы соединяться с другими молекулами.

Существует два вида меток связей:

• Заглавная латинская буква (A..Z) и один из символов + или -. Две поверхности могут соединяться, если их метки связей обозначены одинаковыми буквами, но различными знаками. Например, A+ совместима с A-, но не совместима с A+ и B-.
• Два нуля 00. Метка связи 00 означает, что эта поверхность не может образовывать связь (даже с такой же поверхностью с меткой 00).

Предположим, что в Сборщике имеется неограниченное количество молекул каждого из описанных видов, которые можно поворачивать и переворачивать. При образовании молекулярных структур молекулы могут находиться рядом только, если они совместимы. Каждая поверхность молекулы при этом может быть соединена с ничем.

Рисунок показывает пример молекул трех видов и структуры ограниченного размера, собранной из них (это не единственная возможная структура для заданных типов молекул).



Входные данные. Входные данные состоят из одного теста. Каждый тест состоит из двух строк. Первая строка содержит число n (1 ≤ n ≤ 40000) — количества типов молекул. Вторая строка содержит n подстрок по 8 символов каждая — описание каждого вида молекул, причем поверхности описываются по часовой стрелке.

Выходные данные. Выведите слово unbounded, если молекулы могут создать бесконечную структуру и слово bounded в противном случае.

Решение задачи A
Автор разбора — Василий Астахов, бронзовый медалист ACM ICPC 2011 в составе команды МГУ им. М.В. Ломоносова.

В задаче требуется понять, существует ли неограниченная молекулярная структура, в которой молекулы имеют вид квадратов с различными связями на сторонах. Учитывая доступность операций поворота и отражения, для решения задачи необходимо и достаточно было понять, существует ли цикл из молекул. Тогда, например, смещаясь все время вправо и вниз, можно было бы получить неограниченную на плоскости структуру, при этом никакие связи, кроме соседних по циклу, не были бы задействованы в молекуле. Для нахождения цикла можно было бы построить граф, в котором вершины — это типы соединений, а ребра из типа соединения X[+/−] идут во все типы соединений Y, для которых существует молекула, содержащая одновременно Y и X[−/+] (парную вершину). Тогда, найдя цикл в таком графе, получим существование цикла в исходном. Задача нахождения цикла в ориентированном графе на 52 вершинах (A+, A−, …, Z+, Z−) является несложной и может быть решена, например, алгоритмом построения компонент сильной связности (существование компоненты размером более одной вершины будет означать цикл).

Задача B. Hey, Better Bettor

Недавняя рецессия больно ударила по развлекательным заведениям, в том числе и по игорному бизнесу. Среди казино идет жесткая конкуренция, и, чтобы привлечь игроков, некоторые из них стали проводить особенно привлекательные акции. Акция казино включает следующее: вы можете играть столько, сколько хотите. И после того, как вы закончите, какую бы сумму вы ни проиграли с момента начала, казино возвращает х% ваших потерь. Естественно, если вы оказались в выигрыше, вы забираете его весь.

При этом нет ограничений ни на продолжительность игры, ни на количество денег, с которым вы вступаете в игру, но вы можете воспользоваться этой акцией только один раз.

Для простоты предположим, что все ставки стоят 1 доллар, а выигрыш составляет 2 доллара. Теперь допустим, что х равно 20. Если вы сделаете всего 10 ставок, перед тем как закончить игру, и только 3 из них выиграют, то ваши общие потери составят 3,2 доллара. Если 6 ставок выиграют, то ваш выигрыш составит 2 доллара.

Даны x и p (вероятность выигрыша единичной ставки в процентах), вам требуется написать программу для определения максимального ожидаемого выигрыша, который вы можете получить, используя любую стратегию игры.

Входные данные. Входные данные состоят из одного теста, который содержит процент возврата х (0 ≤ х <100) и вероятность выигрыша в процентах p (0 ≤ p ≤ 50). x и p имеют не более двух цифр после запятой.

Выходные данные. Выведите максимальный ожидаемый выигрыш с абсолютной погрешностью не более 10^-3.

Решение задачи B
Автор разбора — Михаил Левин, бронзовый медалист ACM ICPC 2007 года, серебряный медалист ACM ICPC 2008 года в составе команды МГУ им. М.В. Ломоносова.

Заметим, что решение остановить ли сейчас игру зависит только от текущего выигрыша или проигрыша игрока — история не имеет значения. Можно показать, что оптимальная стратегия в этом случае всегда имеет вид «остановиться, если на руках выигрыш A или проигрыш B», где A и B — некоторые целые неотрицательные числа. При фиксированных A и B для того чтобы вычислить ожидаемую прибыль, необходимо уметь решать такую задачу: найти вероятность P(A, B) того, что игрок в какой-то момент достигнет выигрыша A, при этом ни разу до того не имея на руках проигрыша B или большего. Если эта задача решена, то ожидаемая прибыль стратегии вычисляется как , где x% — скидка, предоставляемая казино игроку в случае проигрыша.

Для чисел P(A, B) выполнено рекуррентное соотношение:

,

где p — вероятность выигрыша при каждом броске монетки. При этом еще P(0, A + B) = 1, а P(A + B, 0) = 0. Если решить эту линейную рекурренту порядка 2, то получим

,

где .

Если бы мы могли перебрать все возможные пары (A, B) для каждого входа (x, p), то мы бы так и сделали, а потом выбрали лучшую. Пар (A, B) бесконечное количество, но если провести несколько численных экспериментов, то можно заметить, что при возрастании A и B ожидаемая прибыль сначала растет, а потом начинает падать (можно доказать выпуклость ожидаемой прибыли как функции от A и B), поэтому всегда достаточно проверить лишь конечное число пар. Кроме того, можно заметить, что наилучшие значения для A и B тем больше, чем ближе p к 0.5, а x — к 100. Худший возможный случай — p = 0.4999, x = 99.99. Оказывается, что в этом случае достаточно перебирать A до 21000, а B — до 2500, и такого перебора достаточно, чтобы решение проходило ограничения по времени.

Задача С. Surely You Congest

Вы отвечаете за систему интеллектуального управления дорожным движением для новых автомобилей. Ваша цель — избежать пробок из водителей, добирающихся из спальных районов в центр города в утренний час пик, используя информацию об устройстве города и движении других автомобилей.

К сожалению, из-за того что водители эгоистичны, они никогда не поедут по не самому короткому из возможных путей в центр, даже если вы попросите их об этом. Вы можете только советовать им, какой из нескольких кратчайших путей выбрать.

Город состоит из перекрестков, соединенных двухсторонними дорогами, которые можно проехать за заданное время. Все водители начинают свое движение на перекрестках (возможно, различных) и заканчивают на одном обозначенном как центр города перекрестке номер 1. Если два водителя одновременно начнут движение по одной и той же дороге в одном направлении, то возникнет пробка и ваша цель будет провалена. Однако водители могут проезжать один и тот же перекресток одновременно или ехать по одной и той же дороге, въехав на нее в разное время.

Определите максимальное количество водителей, которые могут добраться в центр города без пробок, если все водители начинают свое движение одновременно и ни один из них не поедет по неоптимальному пути.



На рисунке машины изображены в их начальном расположении. Один водитель уже находится в центре, а из машин, находящихся на 4 перекрестке, одна может двигаться вдоль пунктирной линии через перекресток 3, другая — вдоль пунктирной линии через перекресток 2, но оставшиеся две не смогут добраться до центра без пробок. Таким образом, ответ на этот тест будет 3.

Входные данные. Вход содержит один тест. Первая строка содержит три числа n, m и c, где n (1≤ n≤ 25000) — количество перекрестков, m (0 ≤ m ≤ 50000) — количество дорог в городе и c (0 ≤ c ≤ 1000) — количество водителей. Каждая из следующих m строк содержит три числа x_i, y_i и t_i, описывающие дорогу, где x_i и y_i (1≤ x_i, y_i ≤ n) — номера различных перекрестков, которые соединяет описанная дорога и t_i (1≤ t_i ≤ 10000) — время, которое должен потратить водитель чтобы добраться от начала до конца дороги в любом направлении. Гарантируется, что можно добраться в центр с любого перекрестка. Последняя строка содержит c чисел, описывающих начальные перекрестки, на которых расположены машины.

Выходные данные. Выведите максимальное количество водителей, которые смогут добраться в центр города без пробок.

Решение задачи С
Автор разбора — Михаил Левин.

Вычислим кратчайшие расстояния d(u) от всех вершин u до конечной вершины e при помощи алгоритма Дейкстры с кучей за O(m log n). Так как все стремятся ехать только по кратчайшему пути, то машины будут ездить только по таким ребрам (u, v) в сторону от u до v, что d(u) = d(v) + l(u, v), где l(u, v) — длина ребра (u, v). Построим новый ориентированный граф, состоящий только из таких ребер.

Для любых двух машин, начавших двигаться одновременно и движущихся от своих исходных точек до конечной точки с одинаковой скоростью, разница расстояний до конечной вершины остается всегда постоянной. Поэтому две машины, начинавшие на разных расстояниях, никогда не могут проехать по одному и тому же ребру одновременно. Сгруппируем все машины по расстоянию от конечной точки. Тогда для каждой группы необходимо найти наибольшее количество попарно непересекающихся по ребрам путей из всех стартовых вершин до конечной вершины в новом ориентированном графе, Эта задача решается при помощи алгоритма нахождения максимального потока в графе: добавим в граф источник и проведем из него ребра во все вершины, в которых есть машины, с пропускной способностью, равной количеству машин в вершине. Все ребра ориентированного графа сделаем пропускной способности 1. Если найти в этом графе максимальный поток из источника в конечную вершину, то как раз и получится максимальное количество попарно не пересекающихся по ребрам путей.

Найдем максимальный поток для каждой группы вершин на одном расстоянии от конечной и сложим ответы — это и будет ответ к задаче. На нахождение одного увеличивающего поток пути уходит O(m), а всего таких путей будет найдено не более c, поэтому суммарно все запуски нахождения максимального потока будут выполнены не более чем за O(mc). Итого сложность решения O(m log n + mc), что проходит в заданные ограничения.

Задача D. Factors

Одна из фундаментальных теорем арифметики гласит, что любое число большее 1 можно единственным образом представить в виде произведения простых чисел. Однако этот уникальный набор простых множителей можно упорядочить различными способами. Например:



Обозначим как f(k) количество различных способов упорядочить простые множители числа k. Тогда f(20) = 3 и f(10) = 2.

Вам дано целое положительное число n, причем гарантируется, что для любого n существует такое k, что f(k) = n. Определите такое минимальное k.

Входные данные. Во входном файле приведены не более 1000 тестов, каждый из которых записан в отдельной строке. Каждый тест состоит из целого положительного числа n < 2⁶³.

Выходные данные. Для каждого теста выведите число n и минимальное k > 1 такое что f(k) = n. Числа в тестах выбраны таким образом, что k < 2⁶³.

Решение задачи D
Автор разбора — Ренат Гимадеев, золотой медалист ACM ICPC 2012 в составе команды Физтеха.

Это довольная простая задача, у которой было много разных решений. Приведу одно из самых коротких.

Заметим, что если разложить на простые сомножители n=p₁^k₁p₂^k₂...p_t^k_t, то количество упорядоченных представлений в виде произведения простых будет равно . Это следует из простых комбинаторных рассуждений: упорядочить N разных простых множителей можно N! способами. Если среди этих множителей есть одинаковые, то все упорядочивания, которые отличаются только порядком одинаковых множителей, на самом деле совпадают. Каждую группу по k_i одинаковых множителей можно переставить k_i! способами. Поэтому каждая уникальная перестановка была посчитана k₁!k₂!...k_t! раз и на это число надо поделить. Эта формула дает нам возможность быстро вычислять f(k), зная разложение числа k на простые множители.

Дальше нужно заметить, что количество упорядочиваний не зависит от того, чему равны p_i и как упорядочены между собой k_i. Поэтому если мы ищем минимальное число, то его надо искать среди чисел вида n=2^k₁3^k₂5^k₃..., причем k₁≥k₂≥k₃≥… Оказывается, что таких чисел среди чисел меньших 2⁶³ не так уж и много (в условии просят искать только те решения, которые меньше 2⁶³), их около 40000 и они легко генерируются рекурсией. Для каждого из них можно найти f(k) по описанной выше формуле и сохранять в ассоциативном массиве минимальные значения числа k для каждого полученного f(k). После этого каждый запрос из условия обрабатывается за время обращения к этому ассоциативному массиву.

Задача E. Harvard

Термин «Гарвардская архитектура» применима к компьютеру с физически разделенной памятью для инструкций и данных. Термин происходит от имени компьютера Harvard Mark I, созданного в 1944 году. В нем для инструкций использовалась бумажная лента, а для данных — реле.

Некоторые современные микроконтроллеры используют «Гарвардскую архитектуру», но не бумажные ленты и реле! Данные лежат в банках, каждый из которых содержит одинаковое число ячеек. Каждая инструкция обращения к данным имеет байт-смещение f в пределах банка и бит a, который используется для определения номера банка. Если a равно 0, то обращение происходит к банку с номером 0. Если a равно 1, то номер банка хранится в специальном регистре выбора банка (РВБ).

Например, пусть у нас есть 4 банка с 8 ячейками каждый. Обратиться к ячейке с номером 5 можно двумя способами: одной инструкцией с a = 0 и f = 5 или двумя инструкциями, установив значение РВБ равным 0 и затем использовав инструкцию с a = 1 и f = 5. Очевидно, что первый способ быстрее, ибо не нужно присваивать значение РВБ. Теперь предположим, что нужно обратиться к ячейке 20 в той же памяти. Сейчас применим только один способ: выполнить инструкцию, установив значение РВБ 2 (если в нем уже не хранится нужное значение), и затем инструкцию с a = 1 и f = 4. Программа представляет собой последовательность операций. Каждая операция это:

• обращение к переменной, записывается как Vi, где i — положительное целое число;
• повторение, записывается как Rn E, где n — положительное целое число, а — произвольная программа, эта операция эквивалентна выполнению программы n раз.
  
  Задача состоит в определении минимального времени выполнения программы. А именно, зная количество и размер банков, а также имея программу, требуется определить минимальное количество инструкций 1(обращения к ячейкам и, возможно, установки значения РВБ) необходимое для выполнения программы. Для этого вам требуется ассоциировать переменные с ячейками памяти и среди всех отображений определить то, которое минимизирует число инструкций. Нужно выдать само это число. Обратите внимание, что значение РВБ до первого присвоения не определено.
  
  Входные данные. Содержат один тест, состоящий из двух строк. В первой b и s — количество и количество переменных, которое можно хранить в банке. Вторая строка содержит непустую программу с не более чем 1000 элементами (каждый из Rn, V i и E считается за один элемент).
  
  Можно предполагать, что:
  
  • в повторении Rn, n удовлетворяет 1≤ n ≤ 10⁶;
  • тело повторения Rn E не пусто;
в обращении к переменной Vi, i удовлетворяет 1 ≤ i ≤ min(bs; 13);
общее число обращений к переменным в программе не превосходит 1012.

    Выходные данные. Выведите одно число — минимальное число инструкций, необходимое для выполнения программы.
    
    Решение задачи E
    Автор разбора — Станислав Пак, золотой медалист ACM ICPC 2009 в составе команды Саратовского государственного университета.
    
    

    Можно сделать наблюдение, что интересных отображений множества переменных на ячейки банков данных достаточно немного, чтобы их все перебрать. А именно (ячейки, задействованные в отображении, будем называть заполненными, аналогично банки, если все их ячейки заполнены):
    
    

    1. Можно считать, что нулевой банк заполнен, если есть другой банк с заполненной ячейкой, потому что обращение к нулевому банку бесплатно.
    2. Банки с номерами больше нуля идентичны, поэтому можно полагать, что минимальные номера переменных, отображенных в ячейки этих банков, упорядочены, например, по возрастанию.
    3. Можно считать, что суммарное количество заполненных ячеек в двух любых банках больше s.

    
    
    С учетом отсечений 1 — 3 и ограничений входных данных интересных отображений около 3 · 10⁶.
    
    Так как обращение к нулевому банку бесплатно, то можно убрать из программы переменные, отображенные на этот банк. Для каждой пары оставшихся переменных i и j можно предпросчитать C_ij — стоимость операции обращения к переменной j после обращения к переменной i, после чего остается смоделировать работу программы.

    
    
    

    Задача F. Low Power

    
    Вы проектируете продвинутые чипы для вычислительных машин. Производство чипов просто и поставлено на рельсы, однако проблему вызывают источники питания, так как доступные батареи имеют различные выходные мощности.
    
    Представьте, что у нас есть n машин с двумя чипами на каждой, а каждый чип питается от k батарей. Удивительно, но не имеет значения, сколько энергии потребляют чипы, однако важно, чтобы выходные мощности чипов как можно меньше отличались друг от друга, так как в этом случае машина работает наилучшим образом. Выходная мощность чипа — это минимальная выходная мощность среди всех k батарей в чипе. Вы располагаете 2nk батареями, которые вам необходимо распределить по чипам машин. Может оказаться, что нет способа распределить батареи так, чтобы выходные мощности чипов были равны для всех машин. Тем не менее, вам нужно минимизировать разность мощностей. Подробнее, вы хотите гарантировать вашим заказчикам, что разность выходных мощностей чипов во всех машинах не превосходит d, при этом стараясь минимизировать d. Для этого вам нужно найти оптимальное распределение батарей по чипам.
    
    Входные данные. Состоят из одного теста, содержащего две строки. В первой строке два числа n и k (2nk ≤ 10⁶), во второй 2nk целых чисел p_i (1 ≤ p_i ≤10⁹).
    
    Выходные данные. Выведите минимальное d такое, что существует распределение батарей по чипам, чтобы разность выходных мощностей чипов в каждой машине не превосходила d.
    
    Решение задачи F
    Автор разбора — Станислав Пак.
    
    

    Эта задача одна из простых. Нужно из 2nk выбрать n пар (назовем их представителями) батареек, каждая из которых
    имеет минимальную мощность на своем чипе, чтобы максимум разности выходных мощностей батареек в паре был минимален. Предположим, что зафиксировано d, тогда можно узнать, существуют ли представители такие, что максимум не превосходит d. Отсортируем мощности p₁ ≤ p₂… ≤ p_2nk и будем жадно набирать пары: в первую пару попадут батареи p₁ и p₂. Если p₂ — p₁ > d, то представителей выбрать нельзя. Во вторую пару возьмем батареи (p_i2, p_i2+1) с разностью не больше d и минимальным индексом i2 ≤ 2k + 1, если это возможно. Аналогично в третью пару — (p_i3, p_{i3 + 1}), i3 ≤ 4k + 1.
    
    Если с помощью этого алгоритма не удается набрать n пар, то этого сделать нельзя. Ответ найдем бинарным поиском.

    
    
    

    Задача G. Map Tiles.

    
    Это задача, которую в отведённое время не смогла решить правильно ни одна из команд.
    
    Печать карт — сложная задачка. Сначала нужно найти подходящее преобразование, чтобы уместить карту сферической земли на плоскости, потом оказывается, что для печати высококачественных карт нужно использовать несколько листов бумаги, потому что на один они не помещаются. Чтобы преодолеть эту трудность, издатели карт разбивают карту на несколько прямоугольных частей и печатают каждую часть отдельно. Именно в этом процессе вы примете участие в этой задаче.
    
    Международная ассоциация издателей карт старается сократить расходы на печать карт минимизируя количество отдельных листов, используемых для печати карт. Даже со стандартным размером листов и масштабом карты можно оптимизировать расход листов, подстраивая их расположение.
    
    В левой части рисунка показаны 14 листов, покрывающие область. В правой части показано, как ту же область можно покрыть всего 10 листами, не изменяя ориентацию области, размер листов и масштаб.
    
    
    Два разных способа разложить по листам Техас
    
    Ваша задача — помочь Международной ассоциации издателей карт найти минимальное количество листов, необходимое для покрытия заданной области. Для простоты область является замкнутым многоугольником без самопересечений.
    
    Обратите внимание, что все листы должны являться частями непрерывной решетки, со сторонами параллельными горизонтали и вертикали. Листы могут касаться только своими сторонами полностью и не могут быть повернуты. Кроме того, хотя все заданные координаты являются целочисленными, листы могут быть расположены в нецелочисленных координатах.
    
    Многоугольник может касаться сторон листов (как в примере 2). Однако, для того чтобы избежать проблем с машинным представлением рациональных чисел, можно предполагать, что ответ не изменится если вершина многоугольника будет находиться снаруди листа на расстоянии 10^-6.
    
    Входные данные. Вход состоит из одного теста. В первой строке теста записаны три числа n, x_s и y_s. Количество вершин многоугольника n (3 ≤ n ≤ 50), x_s и y_s (1≤ x_s, y_s ≤ 100) — размеры листов, которыми нужно покрыть картую. Каждая из следующих n строк содержит два целых числа x и y (0 ≤ x ≤ 10x_s, 0 ≤ y ≤ 10y_s), описывающих вершину многоугольника (в направлении обхода либо по часовой, либо против часовой стрелки).
    
    Выходные данные. Выведите минимальное количество листов, необходимых для покрытия многоугольника.
    
    Решение задачи G
    Автор разбора — Яков Длугач, золотой медалист ACM ICPC 2012 в составе команды Физтеха.
    
    

    Решение этой задачи разбивается на две части: генерацию вариантов расположения многоугольника и подсчёт количества занимаемых клеток для каждого из вариантов расположения.
    
    

    Генерация вариантов

    
    Заметим, что если мы нашли некоторое решение, то его можно «подвинуть», пока многоугольник не упрётся в сетку (то есть дальнейшее движение может изменить набор выбранных клеток). Фактически есть несколько случаев, когда многоугольник упирается в сетку:
    
    

    • одна из вершин многоугольника попадает на линию сетки;
    • одно из рёбер многоугольника натыкается на узел сетки.

    
    
    При выполнении одного из этих условий у многоугольника всё ещё остаётся некоторая степень свободы:
    
    

    • в случае попадания вершины на линию сетки можно двигать многоугольник вдоль этой линии;
    • в случае попадания ребра на узел сетки можно двигать многоугольник вдоль ребра.

    
    
    Заранее оговоримся, что сдвиги, отличающиеся по каждой из координат на число, кратное шагу сетки, мы будем считать равными.
    
    Поэтому фактически есть три варианта выбора «упора», чтобы положение многоугольника относительно сетки задавалось однозначно.
    
    

    1. Одна из вершин попадает на вертикальную линию сетки, и одна из вершин попадает на горизонтальную линию сетки. Сюда входит случай, когда одна вершина попадает в узел сетки. То есть упор однозначно задаётся парой вершин, итого вариантов — n².
    2. Одна из вершин попадает на горизонтальную или вертикальную линию сетки. Без потери общности будем считать, что эта линия сетки — вертикальная и задаётся уравнением x = 0.
       Пусть теперь одно из рёбер, не являющееся вертикальным, попадает на узел. Для выбора сдвига достаточно выбрать абсциссу этого узла, а это можно сделать не более чем m + 1 способами. За m обозначено число 10. Итого вариантов — n²(m + 1).
    3. Два непараллельных ребра упираются в узел сетки. Тут для определения сдвига многоугольника помимо рёбер нужно зафиксировать «разность» между теми узлами сетки, в которые упираются эти рёбра. Итого — n²(m + 1)² вариантов.

    
    
    В результате получаем в худшем случае O(n²m²) вариантов выбора сдвига многоугольника. Поскольку для каждого из вариантов затем нужно будет подсчитать количество занятых клеток, нужно, сгенерировав список всех вариантов, вычистить из него дубликаты: говорят, что это помогало уменьшить количество вариантов в «максимальных» тестах в 3 — 5 раз.
    
    Стоит заметить, что многие команды забывали рассматривать некоторые из этих трёх случаев (большинство команд останавливались только на рассмотрении первого).
    
    

    Подсчёт занимаемых клеток

    
    Вторая сложность в этой задаче состояла в том, чтобы эффективно вычислить количество занимаемых клеток по заданному сдвигу. Наивный способ подсчёта — для (m + 1)² клеток проверить наличие пересечения с многоугольником — работает за O(m²n) и не укладывается в ограничение по времени. Оказывается, что эффективнее будет считать количество занятых клеток в каждом из m + 1 столбцов. Для этого нужно рассмотреть непрерывные куски границы многоугольника, проходящие через столбец: либо кусок границы «пересекает» столбец (один конец куска — на правой границе столбца,
    а другой конец — на левой), либо оба конца куска находятся на одной границе столбца. Можно доказать, что куски первого типа разбиваются на пары, причём все клетки между этими кусками будут заняты. После этого к полученным клеткам нужно добавить клетки, через которые проходят куски второго типа. Этот метод можно реализовать за O(m(m + n)) = O(mn).
    
    Итоговая сложность алгоритма для этой задачи — O(n³m³).

    
    
    

    Задача H. Матрёшка

    
    Матрёшкой называют набор традиционных русских деревянных кукол уменьшающегося размера, помещенных внутрь друг друга. Матрёшку можно открыть, чтобы достать изнутри меньшую матрёшку, у которой, в свою очередь, внутри также есть матрёшка и так далее.
    
    В Национальном Матрёшечном музее недавно проходила выставка матрёшек, на которой были представлены похожие по стилю, но отличающиеся количеством матрёшек в наборе куклы. С сожалению, один шаловливый (и оставленный без присмотра) ребенок разобрал все матрёшки и выставил все куклы в ряд.
    
    В ряду оказалось n матрёшек, про каждую известен её целочисленный размер. Вам нужно заново собрать все матрёшки в наборы, однако вы не знаете ни изначальное количество наборов, ни количество кукол в каждом из наборов. Вы знаете только то, что каждый набор состоит из кукол всех последовательных размеров от 1 до некоторого m, причём m может быть различным для различных наборов.
    
    При сборке наборов нужно руководствоваться следующими правилами:
    
    • можно поместить матрёшку только внутрь матрёшку большего размера;
    • можно объединить две матрёшки только если они стоят рядом в ряду;
    • после того как матрешку помещают внутрь набора матрешек, ее нельзя переместить в другую группу матрешек или отделить от группы матрешек. Разрешается только временно разделить ее при объединении двух групп матрешек.
    
    Ваше время очень ценно, поэтому вы хотите собрать все матрешки в группы как можно быстрее. Единственная часть процесса, которая занимает время, это открытие и после этого закрытие куклы, поэтому вы хотите минимизировать количество именно таких действий. Например, минимальное количество действий для объединения группы [1,2,6] и [4] — два, сначала нужно открыть матрешки размеров 6 и 4. Объединение групп [1,2,5] и [3,4] требует трех открытий.
    
    Напишите программу, которая вычислит минимальное количество открытий, необходимых для сборки всех наборов матрешек.
    
    Входные данные. Вам дан один тест, состоящий из двух строк. Первая строка содержит одно число n (1 ≤ n ≤ 500) — количество отдельных кукол в изначальном ряду. Во второй строке находится n чисел, описывающих размер каждой куклы в ряду. Размер каждой куклы не менее 1 и не превосходит 500.
    
    Выходные данные. Выведите минимальное количество открытий матрешек, необходимое для того, чтобы собрать все наборы. Если сборка невозможна (ребенок мог забрать несколько кукол себе), выведите слово impossible.
    
    Решение задачи H
    Автор разбора —  Алексей Ропан, бронзовый медалист ACM ICPC 2012 в составе команды Белорусского государственного университета информатики и радиоэлектроники.
    
    

    Давайте скажем, что значение F_i — это минимальное количество открытий матрёшек, которые нужно сделать для того, чтобы разбить первые i матрешек по группам. Тогда F₀ = 0 и F_i = min_0≤j<i F_j + G_j+1,i, где значение G_l,r — это минимальное количество открытий, которое нужно сделать, чтобы сложить матрёшки с l по r включительно в одну (нумерация матрешек с единицы), и на интервале от j + 1 до i включительно все размеры матрёшек различные и не превышают i − j. Тогда ответ на задачу будет F_n, а сложность решения без учета вычисления значений G будет O(n²). Для G_i,i значение всегда равно 0, а для G_i,j и i < j на последнем этапе происходит объединение двух групп матрёшек. Пусть k — это номер матрёшки, на которой заканчивается левая группа. Тогда G_i,j = min_i≤k<j G_i,k + G_k+1,j + C_i,k,j, где значение C_i,k,j — это минимальное количество открытий матрёшек, которое потребуется для того, чтобы объединить группы матрёшек с i-й по k-ю и c k+1-й по j-ю. Пусть значение M_i,j — это минимальный размер матрёшки на интервале от i до j и значение K_i,j,s — количество матрёшек на интервале от i до j, размеры которых меньше s. Тогда C_i,k,j можно посчитать как j − i + 1 − t, где t — это количество матрёшек, которые при объединении не будут открыты, то есть t = K_k+1,j,Mi,j + K_i,j,Mk+1,j (можно заметить, что одно из слагаемых всегда будет равно нулю). Сложность вычисления K и G равна .

    
    
    

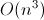    Задача I. Pirate Chest

    
    Пират Джек устал от битв, мародерства, воровства и угнетения всех и вся в открытом море. Он решил уйти на пенсию, и даже нашел идеальный необитаемый островок в океане, на котором он достойно проведет остаток жизни, если у него, конечно, не закончатся деньги. Сейчас у него много золотых монет, которые он хочет сложить в сундук (он же в конце концов пират!). Джек может построить сундук в форме прямоугольного параллелепипеда с целочисленными сторонами и не превышающими заданный размерами дна сундука. Осталось лишь найти, куда спрятать сундук с сокровищами.
    
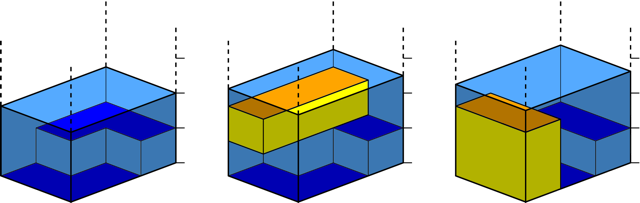
    Джек решил затопить сундук в тенистом пруду. Поверхность пруда представляет собой прямоугольник с заданными сторонами, пруд со всех сторон окружен вертикальными каменными берегами. Джек исследовал дно пруда и знает про каждый квадрат 1х1 пруда (в декартовой системе координат) глубину пруда в этом месте. Когда Джек утопит сундук, последний утонет на максимально возможную глубину до тех пор, пока не коснется дна хотя бы одним квадратом. Из-за утопленного сундука уровень воды в пруду поднимется. Берега пруда достаточно высоки, чтобы вода никогда не вылилась за его границы. Разумеется, так как сундук нужно спрятать, он должен полностью находиться ниже уровня воды в пруду. Ваша задача — найти максимальный объем сундука, который можно спрятать в пруду.
    
    На рисунке слева показан пруд без сундука, по центру — пруд в котором находится сундук объема 3, справа — сундук объема 4 (максимально возможного) в пруду. Обратите внимание, что если бы сундук с центрального рисунка был сделан на единицу большей высоты, то его верх был бы виден ровно на поверхности пруда.
    
    
    
    Входные данные. Вход содержит один тест. Тест начинается со строки, содержащей четыре целых числа a, b, m, n (1≤ a,b,m,n ≤ 500). Размеры поверхности пруда — m x n, максимальный размер дна сундука — a x b. Кроме того, a и b достаточно, сундук никогда не покроет весь пруд полностью. Каждая из оставшихся m строк входа содержит n чисел d_ij, описывающих глубину пруда в квадрате с координатами (i,j), где 0≤ d_ij ≤ 10⁹ для любого 1≤ i ≤ m, 1≤ j ≤ n.
    
    Выходные данные. Выведите максимальный объем сундука с целочисленными сторонами, который можно спрятать в пруду под поверхностью воды, причем одно из измерений дна должно не превышать a, а другое — не превышать b. Если ни один сундук нельзя спрятать под водой, то выведите 0.
    
    Решение задачи I
    Автор разбора — Василий Астахов.
    
    

    Для начала заметим, что если у нас есть участок дна размером h · w, глубиной хотя бы d, то мы можем положить туда сундук объемом , где S — площадь всего пруда. Отсюда получаем, что чем больше h · w, тем больший объем сундука мы можем погрузить, при фиксированном d. Перейдём теперь к решению задачи. По сути нам нужно проверить все прямоугольники (размером не превосходящем (a,b)) найти у них минимальную глубину дна, найти объем по формуле и выбрать максимум.
    
    Но такое решение будет работать слишком долго. Для ускорения работы, мы зафиксируем только x₀ и x₁ координаты прямоугольника (x₀<x₁, x₁-x₀ ≤ b). Таким образом, мы имеем дело с полосками, идущими от x₀ координаты до x₁. Посчитаем на каждой из них минимальную глубину (это можно сделать например препроцессингом за n³). Теперь заметим, что если w=x₁-x₀≤ a, то имеем ограничение на длину по y b, иначе длина по y меньше или равна a. Теперь задача свелась к одномерной: нам нужно найти такой отрезок (с указанным ограничением на его длину h), чтобы значение объема было максимальным. Отсортируем глубины всех отрезков начиная с максимальной. Введем двусторонний список индексов по оси y. По ходу действия алгоритма мы будем рассматривать индексы, начиная с максимальной глубины, а после обработки удалять их из списка.
    
    Так для каждого элемента мы будем знать номер ближайшего слева и справа элементов с меньшей глубиной (в плане индекса в массиве отсортированных глубин), чем уже отработаны. Таким образом, весь отрезок между ними имеет глубину ≥ текущей обрабатываемой. Значит, найдем минимум между его длиной и ограничение на длину отрезка и сравним с наилучшим ответом по формуле для объема. Таким образом, время работы алгоритма O(n² · m · log m ), где log берется из сортировки.

    
    
    

    Задача J. Pollution Solution

    
    Будучи сотрудником отделения природопользования и охраны окружающей среды, вы должны следить за отходами, которые сбрасываются (иногда случайно, иногда специально) в реки, озёра и океаны. Одна из ваших задач — измерение влияния загрязнения на различные водные экосистемы, такие как коралловые рифы, места нереста и так далее.
    
    
    
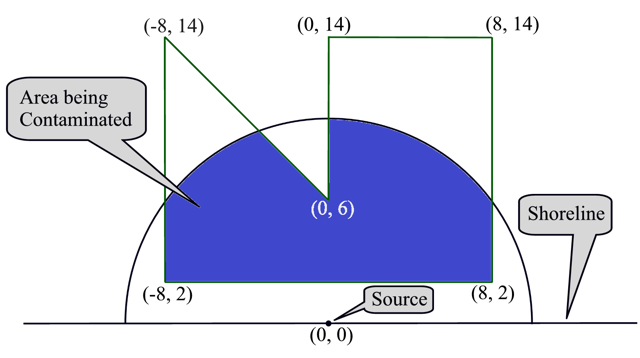
    Модель, которую вы используете при анализе, изображена на рисунке. Береговая линия (горизонтальная линия на рисунке) лежит на оси x, источник загрязнения расположен в начале координат (0, 0).
    Распространение загрязнения в воду представляется полукругом, а многоугольник означает интересующую вас экосистему. Вам требуется определить площадь экосистемы, которая подверглась загрязнению, то есть площадь тёмно-синей области на рисунке.
    
    Входные данные. Вход содержит один набор тестовых данных. Тест начинается строкой, содержащей два целых числа n и r, где 3 ≤ n ≤ 100 — это количество вершин многоугольника, 1 ≤ r ≤ 1000 — это радиус поля загрязнения. Следом идут n строк, каждая содержит по два целых числа x_i и y_i — координаты вершин многоугольника в порядке против часовой стрелки, причём −1500 ≤ x_i ≤ 1500 и 0 ≤ y_i ≤ 1500. Многоугольник не имеет самопересечений и самокасаний. Никакая вершина не лежит на окружности.
    
    Выходные данные. Выведите площадь части многоугольника, которая попадает в полукруг с центром в начале координат радиуса r. Дайте ответ с абсолютной погрешностью не более 10⁻³.
    
    Решение задачи J
    Автор разбора — Сергей Соболь, серебряный медалист ACM ICPC 2012 в составе команды Белорусского государственного университета.
    
    

    Это геометрическая задача с незамысловатым условием: требуется вычислить площадь пересечения полукруга и многоугольника, заданных на плоскости.
    
    Рассмотрим вначале удобный способ вычисления площадей произвольных простых многоугольников (без самопересечений, но не обязательно выпуклых). Пусть O — начало координат, а многоугольник задаётся n точками P₁, P₂, …, P_n в порядке обхода, которые можно отождествить с n двумерными радиус-векторами (x_i, y_i). Для простоты записи формул будем полагать, что P_n+1 = P₁. Тогда площадь фигуры выражается формулой
    
    ,
    
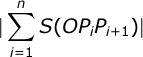    где S(O P_i P_i+1) — ориентированная площадь треугольника с вершинами O, P_i и P_i+1:
    
    .
    
    Эта величина по модулю равна площади треугольника, а знак её зависит от относительного расположения точек:
    
    
    
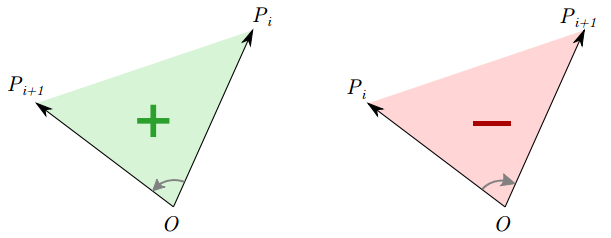
    Когда суммируются все n таких значений, площади «лишних» частей треугольников, лежащих вне многоугольника, взаимно уничтожаются и остаётся лишь искомая площадь многоугольника, итоговый знак которой зависит от порядка обхода точек (по часовой стрелке или против).
    
    
    
    Вернёмся к нашей задаче. Заметим, что вместо полукруга можно рассматривать и целый круг, при этом ничего не поменяется, потому что многоугольник всегда лежит в верхней полуплоскости. Воспользуемся той же идеей: будем по очереди пересекать каждый треугольник OP_iP_i+1 с кругом и суммировать площади, которые получаются, с учётом ориентации.
    
    
    
    Как найти площадь пересечения одного такого треугольника и заданного круга? Сначала стоит найти точки пересечения отрезка P_iP_i+1 с окружностью. Это можно делать разными способами.
    
    

    • Каждая точка отрезка имеет вид t P_i + (1 − t) P_i+1 при некотором t из [0, 1] (параметрическое уравнение отрезка). Можно расписать расстояние от точки до начала координат в зависимости от t, приравнять его к радиусу окружности и решить квадратное уравнение.
    • Исходя из чисто геометрических соображений можно придти к более красивым результатам.

    
    
    Легко видеть, что отрезок может иметь с окружностью одну (как P₁P₂ и P₃P₄ на рисунке), две точки пересечения (P₅P₁) или не иметь ни одной (отрезки P₂P₃ и P₄P₅).
    
    Область пересечения круга и каждого из треугольников OP_iP_i+1 тогда разобьётся на отдельные треугольники и сектора (например, для треугольника OP₅P₁ это будут два сектора и треугольник). В решении придётся сделать разбор случаев (по сути все они изображены на рисунке), что не очень приятно, но в целом не сложно. Для площадей треугольника и сектора есть общеизвестные формулы.
    
    Таким образом, задача решается за время .

    
    
    

    Задача K. Up a Tree

    
    Анатолий — типичный студент во многих смыслах. Всякий раз он пытается копипастить код вместо написания с нуля. Такой подход неизбежно доставляет ему проблемы. Например, когда он впервые познакомился с разными порядками обхода бинарных деревьев post, pre и in и получил код pre-обхода с вызовом функции вывода вершины output, он просто скопировал код, перенес вызов output в правильное место и переименовал функцию. Однако он забыл переименовать функции в теле обхода, получив неправильные функции обходов.
    
    Пример кода и результат копипасты с правками.
    

    void prePrint(TNode t)
    {
        output(t.value);
        if (t.left != null)
            prePrint(t.left);
        if (t.right != null)
            prePrint(t.right);
    }
    void inPrint(TNode t)
    {
        if (t.left != null)
            prePrint(t.left);
        output(t.value);
        if (t.right != null)
            prePrint(t.right);
    }
    void postPrint(TNode t)
    {
        if (t.left != null)
            prePrint(t.left);
        if (t.right != null)
            prePrint(t.right);
        output(t.value);
    }

    
    
    И тут Анатолий проявил себя не как типичный студент — он стал тестировать свой код! К сожалению, когда он увидел, что функции работаю неправильно, он стал вести себе как обычный студент снова. Он стал паниковать и случайным образом переименовывать вызовы функций во всех трех обходах, надеясь, что они начнут работать правильно.
    
    Преподаватель Анатолия тестировал его код на случайных деревьях с символами в вершинах. Когда она посмотрела на выходные данные программы, то поняла, что случилось. Тем не менее, вместо того, чтобы посмотреть код, она попробовала восстановить код по его выводу. Для этого она сделала справедливые предположения:
    
    
    • команда вывода символа находится на правильном месте, например, между вызовами функций в inPrint обходе;
    • среди всех 6 рекурсивных вызовов ровно по два вызова inPrint, prePrint и postPrint, возможно, стоящих в неправильных местах.
    
    Вскоре преподаватель поняла, что восстановление кода Анатолия и тестового дерева по выводу программы не такая простая задача и что результат может быть неоднозначным. Вам предстоит помочь ей найти все возможные реконструкции кода Анатолия. Вдобавок, для каждого восстановленного кода необходимо найти лексикографически наименьшее дерево по выходным данным программы.
    
    Входные данные. Состоят из одного теста, содержащего три строки — выходные строки функций соответственно prePrint, inPrint и postPrint. Строки имеею одинаковую длину n (4 ≤ n ≤ 26), все символы каждой из строк различны.
    
    Выходные данные. Для каждого восстановления в отдельную строку выведите 6 слов из множества {Pre, In, Post} — префиксы имен функций в теле prePrint в порядке следования в коде, имена функций в теле inPrint и, наконец, postPrint. Далее, в трех остальных строках выведите результаты правильных prePrint, inPrint, postPrint функций на тестовом дереве, на котором эти результаты лексикографически минимальны, то есть результат prePrint минимально возможный, среди всех таких деревьев, такое, на котором результат inPrint минимален.
    
    Решение задачи K
    Автор разбора — Егор Куликов, бронзовый медалист ACM ICPC 2007 года в составе команды МГУ им. М.В. Ломоносова.
    
    

    Давайте для начала переберём вариант расстановки вызовов функций. Таких вариантов всего 90. Пусть расстановка вызовов фиксирована. Далее мы можем посчитать ответ динамическим программированием. В качестве состояния возмём S(f₁, f₂, f₃, s₁, s₂, s₃, l) — существует ли дерево, которое, если его напечатать функцией f_i, будет подстрокой i-й строки входных данных, начинающейся в позиции s_i и имеющей длину l, и если да — то найти такое дерево с лексикографически минимальной префиксной записью, а если и таких несколько — с лексикографически минимальной инфиксной записью.
    
    В каждой позиции мы можем просто перебрать число вершин в левом поддереве текущего поддерева, таким образом время работы динамического перехода O(n²).
    
    Теоретически существует 3³ n⁴ возможных положений, но так как для положительного ответа набор букв в каждой подстроке должен совпадать, то содержательных позиций не более 3³ n², при n ≤ 26 это легко укладывается в ограничения по времени и памяти.
    
    

    
    
    Конечно, это не единственный существующий разбор задач ACM ICPC 2013, есть и другие. Например, можете посмотреть на разбор, который опубликовал доцент Королевского технологического института Швеции Per Austrin (на английском). В разные годы он также бывал и участником, и судьёй ICPC. Оригиналы задач вы можете найти здесь.