При выполнении запросов в ClickHouse можно обратить внимание, что в профайлере на одном из первых мест часто видна функция LZ_decompress_fast. Почему так происходит? Этот вопрос стал поводом для целого исследования по выбору лучшего алгоритма разжатия. Здесь я публикую исследование целиком, а короткую версию можно узнать из моего доклада на HighLoad++ Siberia.
Данные в ClickHouse хранятся в сжатом виде. А во время выполнения запросов ClickHouse старается почти ничего не делать — использовать минимум ресурсов CPU. Бывает, что все вычисления, на которые могло тратиться время, уже хорошо оптимизированы, да и запрос хорошо написан пользователем. Тогда остаётся выполнить разжатие.
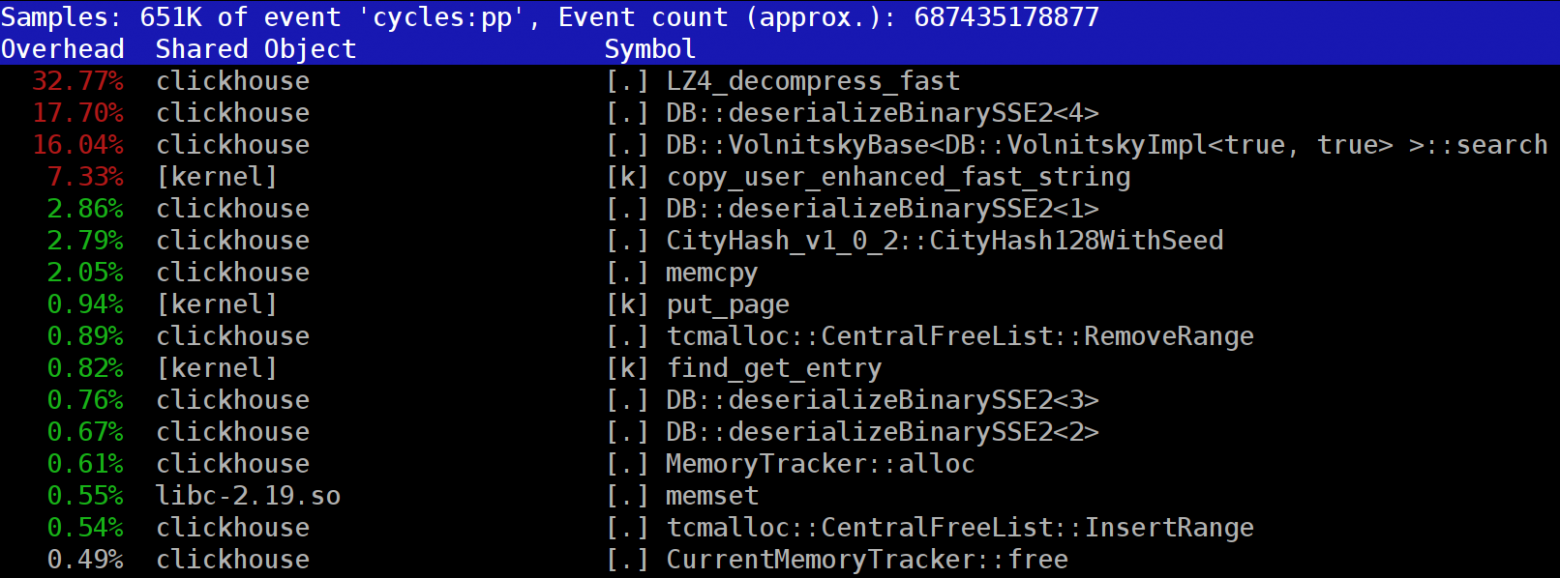
Вопрос — почему разжатие LZ4 может быть узким местом? Казалось бы, LZ4 — очень лёгкий алгоритм: скорость разжатия, в зависимости от данных, обычно составляет от 1 до 3 ГБ/с на одно процессорное ядро. Это уже существенно больше скорости работы дисковой подсистемы. Более того, мы используем все доступные ядра, а разжатие линейно масштабируется по всем физическим ядрам.
Но следует иметь в виду два момента. Во-первых, с диска читаются сжатые данные, а скорость разжатия приведена в количестве несжатых данных. Если коэффициент сжатия достаточно большой, то с дисков почти ничего не надо считывать. Но при этом разжатых данных образуется много, и разумеется, это влияет на расход CPU: объём работы по разжатию данных в случае LZ4 почти пропорционален объёму самих разжатых данных.
Во-вторых, чтение данных с дисков может не требоваться вообще, если данные находятся в кэше. Для этого можно полагаться на page cache или использовать свой собственный кэш. В столбцовых БД использование кэша более эффективно за счёт того, что в него попадают не все столбцы, а только часто используемые. Вот почему LZ4 в смысле нагрузки на CPU часто является узким местом.
Отсюда ещё два вопроса. Если разжатие данных «тормозит», то может, их вообще не стоит сжимать? Но на практике это предположение бессмысленно. Недавно в ClickHouse можно было настроить всего два варианта сжатия данных — LZ4 и Zstandard. По умолчанию используется LZ4. Переключившись на Zstandard, можно сделать сжатие сильнее и медленнее. А вот полностью отключить сжатие ещё совсем недавно было нельзя — LZ4 рассматривается как разумный минимум, который можно использовать всегда. Именно поэтому я очень люблю LZ4. :)
Но недавно в англоязычном чате поддержки ClickHouse появился таинственный незнакомец, который рассказал, что у него очень быстрая дисковая подсистема (NVMe SSD) и всё упирается в сжатие — неплохо было бы иметь возможность его выключить. Я ответил, что такой возможности нет, но её легко добавить. Через несколько дней нам пришёл пул-реквест, в котором реализуется метод сжатия
Второй возникающий вопрос: если есть кэш, почему бы не хранить в нём уже разжатые данные? Это допускается — во многих случаях так удастся избавиться от необходимости разжатия. И в ClickHouse есть такой кэш — кэш разжатых блоков. Но на него жалко тратить много оперативки из-за его низкой эффективности. Он оправдывает себя только на мелких, идущих подряд запросах, которые используют почти одни и те же данные.
Общее соображение: данные надо сжимать, желательно всегда. Всегда записывайте их на диск со сжатием. Передавайте по сети тоже со сжатием. На мой взгляд, сжатие по умолчанию следует считать оправданным даже при передаче в 10-гигабитной сети без переподписки в пределах дата-центра, а передавать данные без сжатия между дата-центрами вообще недопустимо.
Почему же используется именно LZ4? Можно ли подобрать нечто ещё более лёгкое? В принципе, можно, и это правильно и полезно. Но давайте сначала рассмотрим, к какому классу алгоритмов относится LZ4.
Во-первых, он не зависит от типа данных. К примеру, если вы заранее знаете, что у вас будет массив целых чисел, то можете использовать один из многочисленных вариантов алгоритма VarInt — так будет эффективнее по CPU. Во-вторых, LZ4 не слишком сильно зависит от требуемых допущений на модель данных. Предположим, у вас есть упорядоченный временной ряд показаний датчика — массив с числами типа float. Тогда вы можете посчитать дельты, а затем сжимать дальше, и это будет эффективнее по коэффициенту сжатия.
То есть LZ4 можно без проблем использовать для любых массивов байтов — для любых файлов. Конечно, у него есть своя специализация (об этом ниже), и в некоторых случаях его использование бессмысленно. Но если его назвать алгоритмом общего назначения, это будет небольшой ошибкой. И заметим, что, благодаря внутреннему устройству, LZ4 в качестве частного случая автоматом реализует алгоритм RLE.
Другой вопрос: неужели LZ4 — наиболее оптимальный алгоритм данного класса по совокупности скорости и силы сжатия? Такие алгоритмы называются pareto frontier — это значит, что не существует другого алгоритма, который строго лучше по одному показателю и не хуже по другим (да ещё и на широком множестве датасетов). Есть алгоритмы, которые быстрее, но дают меньший коэффициент сжатия, а есть те, которые сжимают сильнее, но при этом медленнее сжимают или разжимают.
На самом деле LZ4 — не pareto frontier. Есть варианты, которые чуть-чуть лучше. Например, это LZTURBO от некоего powturbo. В достоверности результатов можно не сомневаться благодаря сообществу на encode.ru (крупнейшем и примерно единственном форуме по сжатию данных). Но разработчик не распространяет ни исходники, ни бинарники, а только даёт их ограниченному кругу лиц для тестирования или за кучу денег (вроде никто до сих пор не заплатил). Также стоит обратить внимание на Lizard (бывший LZ5) и Density. Они могут работать чуть лучше LZ4 при выборе некоторого уровня сжатия. Также обратите внимание на LZSSE — крайне интересная вещь. Впрочем, посмотреть на неё лучше после прочтения этой статьи.
Давайте рассмотрим, как вообще работает LZ4. Это одна из реализаций алгоритма LZ77: L и Z указывают на фамилии авторов (Лемпель и Зив), а 77 — на 1977 год, когда алгоритм был опубликован. У него множество других реализаций: QuickLZ, FastLZ, BriefLZ, LZF, LZO, а также gzip и zip в случае использования низких уровней сжатия.
Сжатый с помощью LZ4 блок данных содержит последовательность записей (команд, инструкций) двух видов:
Пример. До сжатия:
После сжатия:
Если взять сжатый блок и пройтись по нему курсором, выполняя эти команды, то мы получим в качестве результата исходные, разжатые данные.
Мы примерно рассмотрели, как данные разжимаются. Также ясна суть: для выполнения сжатия алгоритм кодирует повторяющиеся последовательности байт с помощью матчей.
Ясны и некоторые свойства. Этот алгоритм byte-oriented — он не препарирует отдельные байты, а лишь копирует их целиком. Здесь кроется отличие, например, от энтропийного кодирования. Для примера, zstd является композицией LZ77 и энтропийного кодирования.
Заметим, что размер сжатого блока выбирается не слишком большим, чтобы не тратить много оперативки во время разжатия; чтобы не сильно замедлить random access в сжатом файле (который состоит из множества сжатых блоков); и иногда — чтобы блок помещался в какой-нибудь кэш CPU. Например, можно выбрать 64 КБ — так буферы для сжатых и несжатых данных поместятся в L2-кэш и половина ещё останется.
Если нам потребуется сжать файл большего размера, мы просто будем конкатенировать сжатые блоки. Заодно рядом с каждым сжатым блоком удобно расположить дополнительные данные — размеры, чек-сумму.
Максимальное смещение для матча ограничено, в LZ4 — 64 килобайтами. Эта величина называется sliding window. Действительно, это значит, что по мере продвижения курсора вперёд совпадения могут находиться в окне размером 64 килобайта до курсора, которое движется вместе с курсором.
Теперь рассмотрим, как сжать данные — другими словами, как найти в файле совпадающие последовательности. Конечно, вы можете использовать suffix trie (классно, если вы о нём слышали). Есть варианты, при которых в процессе сжатия среди предыдущих байт гарантированно находится самая длинная совпадающая последовательность. Это называется optimal parsing и даёт почти лучший коэффициент сжатия для фиксированного формата сжатого блока. Но есть и более эффективные варианты — когда мы находим какое-нибудь достаточно хорошее совпадение в данных, но не обязательно самое длинное. Самый эффективный способ его найти — использовать хэш-таблицу.
Для этого проходимся по исходному блоку данных курсором и берём несколько байт после курсора. Например, 4 байта. Хэшируем их и кладём в хэш-таблицу смещение от начала блока — где эти 4 байта встретились. Величина 4 называется min-match — с помощью такой хэш-таблицы мы можем отыскать совпадения минимум в 4 байта.
Если мы посмотрели в хэш-таблицу, а там уже есть запись, и если смещение не превышает sliding window, то мы проверяем, сколько ещё байт совпадает после этих четырёх байт. Может быть, там ещё много чего совпадает. Возможно и такое, что в хэш-таблице возникла коллизия и не совпадает ничего. Это нормально — можно просто заменить значение в хэш-таблице на новое. Коллизии в хэш-таблице будут просто приводить к меньшему коэффициенту сжатия, поскольку найдётся меньше совпадений. Кстати, такой вид хэш-таблиц (фиксированного размера и без разрешения коллизий) называется cache table, кэш-таблица. Это тоже логично — в случае коллизии кэш-таблица просто забывает про старую запись.
Итак, я хочу ускорить разжатие LZ4. Давайте посмотрим, что из себя представляет цикл разжатия. Вот этот цикл в псевдокоде:
Формат LZ4 устроен так, что в сжатом файле литералы и матчи чередуются. И очевидно, первым всегда идёт literal (потому что с самого начала матч ещё неоткуда взять). Поэтому их длины кодируются вместе.
На самом деле всё чуть-чуть сложнее. Из файла читается один байт, и из него берутся две половинки (nibble), в которых закодированы числа от 0 до 15. Если соответствующее число не равно 15, то оно считается длиной литерала и матча соответственно. А если оно равно 15, то длина больше и она закодирована в следующих байтах. Тогда считывается следующий байт, и его значение прибавляется к длине. Далее, если оно равно 255, то мы продолжаем — считываем следующий байт так же.
Отметим, что максимальный коэффициент сжатия для формата LZ4 не достигает 255. И второе (бесполезное) наблюдение: если ваши данные очень избыточны, то применение LZ4 дважды позволит увеличить коэффициент сжатия.
Когда мы прочитали длину литерала (а затем так же — длину матча и смещение матча), для разжатия достаточно просто скопировать два фрагмента памяти.
Казалось бы, можно использовать функцию
Почему использовать функцию memcpy неоптимально? Потому что она:
Последний пункт самый важный. Допустим, мы попросили функцию memcpy скопировать ровно 5 байт. Было бы очень хорошо скопировать сразу 8 байт, использовав для этого две инструкции movq.
Но тогда мы скопируем три лишних байта — то есть будем писать за границу переданного буфера. Функция
Но в нашем случае мы почти всегда можем писать лишние байты. Можем считывать лишние байты в input-буфере до тех пор, пока лишние байты расположены в нём целиком. При тех же условиях мы можем записать лишние байты в output-буфер — потому что на следующей итерации мы их всё равно перезапишем.
Эта оптимизация уже есть в оригинальной реализации LZ4:
Чтобы воспользоваться такой оптимизацией, нужно лишь проверять, что мы находимся достаточно далеко от границы буфера. Это должно быть бесплатно, потому что мы и так проверяем выход за границы буфера. А обработку последних нескольких байт — «хвостика» данных — можно делать уже после основного цикла.
Впрочем, всё равно есть некоторые тонкости. В цикле два копирования — литерала и матча. Но при использовании функции LZ4_decompress_fast (вместо LZ4_decompress_safe) проверка выполняется один раз — когда нам нужно скопировать литерал. При копировании матча проверка не выполняется, но в самой спецификации формата LZ4 есть условия, которые позволяют её избежать:
Специально подобранные входные данные могут вызвать «проезд» по памяти. Если вы используете функцию LZ4_decompress_fast, вам нужна защита от плохих данных. Сжатые данные надо по крайней мере чек-суммировать. А если вам нужна защита от злоумышленника, то используйте функцию LZ4_decompress_safe. Другие варианты: берите криптографическую хэш-функцию в качестве чек-суммы, но это почти наверное убьёт всю производительность; либо выделяйте больше памяти для буферов; либо выделяйте память для буферов отдельным вызовом mmap и создайте guard page.
Когда я вижу код, который копирует данные по 8 байт, сразу спрашиваю — а почему именно по 8 байт? Можно копировать по 16 байт, используя SSE-регистры:
Аналогично работает копирование 32 байт для AVX и 64 байт для AVX-512. Кроме того, можно развернуть цикл в несколько раз. Если вы когда-нибудь смотрели, как реализована
Почему в оригинальной реализации LZ4 так не сделано? Во-первых, неочевидно, лучше это или хуже. Результат зависит от размеров фрагментов, которые нужно копировать. Вдруг они все короткие и лишняя работа будет ни к чему? А во-вторых, это рушит те условия в формате LZ4, которые позволяют избежать лишнего бранча во внутреннем цикле.
Тем не менее, будем пока держать этот вариант в уме.
Вернёмся к вопросу — всегда ли можно таким образом копировать данные? Предположим, нам нужно скопировать матч — то есть скопировать фрагмент памяти из output-буфера, находящийся на некотором смещении позади от курсора, в позицию этого курсора.
Представим простой случай — нужно скопировать 5 байт по смещению 12:
Но есть более сложный случай — когда нам нужно скопировать фрагмент памяти, длина которого больше смещения. То есть он частично указывает на данные, которые ещё не были записаны в output-буфер.
Копируем 10 байт по смещению 3:
В процессе сжатия у нас есть все данные, и такой матч вполне может найтись. Функция
Вот как это работает:
То есть мы должны создать повторяющуюся последовательность. В оригинальной реализации LZ4 для этого написан удивительно непонятный код:
Мы копируем первые 4 байта побайтово, смещаемся на какое-то магическое число, копируем следующие 4 байта целиком, смещаем указатель на match на другое магическое число. Автор кода (Ян Коллет) по какой-то нелепой причине забыл оставить комментарий, что это значит. К тому же имена переменных запутывают. Обе называются dec...table, но одну из них мы прибавляем, а другую — вычитаем. Кроме того, ещё одна из них имеет тип unsigned, а другая — int. Впрочем, стоит отдать должное: как раз недавно автор улучшил это место в коде.
Вот как на самом деле это работает. Копируем первые 4 байта побайтово:
Теперь можно скопировать 4 байта сразу:
Можно продолжить как обычно, копируя 8 байт сразу:
Как вы знаете из опыта, иногда лучший способ понять код — это переписать его. Вот что получилось:
Производительность, конечно же, не изменилась никак. Впрочем, я очень хотел попробовать оптимизацию, в которой обычное копирование — сразу по 16 байт.
Но это усложняет «особый случай» и приводит к тому, что он вызывается чаще (условие
Можно ли реализовать именно эту функцию оптимальнее? Хотелось бы, чтобы для такого сложного кода нашлась магическая SIMD-инструкция, ведь мы всего лишь хотим записать 16 байт, которые целиком состоят из нескольких байт входных данных (от 1 до 15). Их, в свою очередь, нужно просто повторить в правильном порядке.
Такая инструкция есть — она называется
Вот пример:
Каждый байт результата мы заполнили выбранным нами байтом исходных данных — это как раз то что надо! Вот как выглядит код в результате:
Здесь
Можно ли сделать такую операцию для большего числа байт сразу, используя более новые инструкции? Ведь SSSE3 — очень старый набор инструкций, существующий с 2006 года. В AVX2 есть инструкция, которая делает это сразу для 32 байт, но только независимо для отдельных 16-байтных фрагментов. Она называется уже не packed shuffle bytes, а vector permute bytes — слова другие, а смысл такой же. В AVX-512 VBMI есть ещё одна инструкция, работающая сразу для 64 байт, но процессоры с её поддержкой появились совсем недавно. Похожие инструкции также есть в ARM NEON — они называются vtbl (vector table lookup), но позволяют записывать только 8 байт.
Кроме того, существует вариант инструкции
На конференции Highload++ Siberia после моего доклада ко мне подошёл слушатель и сказал, что для случая 8 байт можно просто использовать умножение на специально подобранную константу (также потребуется сдвиг) — я об этом раньше даже не думал!
Допустим, я хочу использовать вариант, копирующий по 16 байт. Как избежать необходимости дополнительной проверки выхода за границы буфера?
Я решил, что вообще не буду делать эту проверку. В комментарии к функции будет написано, что разработчику следует выделить кусок памяти на указанное количество байт больше, чем требуется, чтобы позволить нам читать и писать туда ненужный мусор. Интерфейс функции станет неудобным, но это уже другие проблемы.
Впрочем, могут возникнуть негативные последствия. Допустим, данные, которые нам надо разжимать, были сформированы из блоков по 65 536 байт. Тогда пользователь даёт нам фрагмент памяти размером 65 536 байт для разжатых данных. Но с новым интерфейсом функции пользователь будет обязан выделить фрагмент памяти, например, из 65 551 байта. Тогда аллокатор, вполне возможно, будет вынужден на самом деле выделить 96 или даже 128 килобайт — в зависимости от его реализации. Если же аллокатор очень плохой, он может внезапно перестать кэшировать фрагмент памяти у себя в «куче» и начать каждый раз использовать mmap для выделения памяти (либо освобождать память с помощью madvice). Такой процесс будет ужасно медленным из-за page faults. В итоге маленькая попытка оптимизации может привести к тому, что всё начнёт тормозить.
Итак, я сделал вариант кода, в котором применены три оптимизации:
Я стал тестировать этот код на самых разных наборах данных и получил неожиданные результаты.
Пример 1:
Xeon E2650v2, данные Яндекс.Браузера, столбец AppVersion.
reference: 1.67 GB/sec.
16 bytes, shuffle: 2.94 GB/sec (на 76% быстрее).
Пример 2:
Xeon E2650v2, данные Яндекс.Директа, столбец ShowsSumPosition.
reference: 2.30 GB/sec.
16 bytes, shuffle: 1.91 GB/sec (на 20% медленнее).
Сначала я увидел, что всё ускорилось на десятки процентов и успел обрадоваться. Потом на других файлах увидел, что ничего не ускорилось. Ещё на каких-то замедлилось, хоть и ненамного. Я сделал вывод, что результаты зависят от коэффициента сжатия. Чем больше сжат файл — тем больше преимущество от перехода на 16 байт. Это естественно: чем больше коэффициент сжатия, тем больше средняя длина фрагментов, которые нужно копировать.
Чтобы лучше разобраться, я с помощью шаблонов C++ сделал варианты кода для четырёх случаев: оперируем 8- или 16- байтными кусочками; используем или не используем shuffle-инструкцию.
На разных файлах выигрывали совершенно разные варианты кода, но при тестировании на рабочем компьютере вариант с shuffle всегда выигрывал. На рабочем компьютере тестировать неудобно, приходится делать так:
Потом я пошёл на один из старых «разработческих» серверов (c процессором Xeon E5645), достал ещё больше наборов данных и получил почти диаметрально противоположные результаты, которые меня окончательно запутали. Выяснилось, что выбор оптимального алгоритма определяется не только коэффициентом сжатия, но и моделью процессора. От неё зависит то, когда лучше использовать shuffle-инструкцию, а также порог, начиная с которого лучше использовать 16-байтные копирования.
Кстати при тестировании на серверах имеет смысл делать так:
Иначе результаты будут нестабильными. Также следите за thermal throttling и power capping.
Итак, у нас есть четыре варианта алгоритма, и нужно в зависимости от условий выбирать лучший. Можно было бы создать репрезентативный набор данных и железа, затем провести хорошее нагрузочное тестирование и выбрать тот метод, который лучше в среднем. Но у нас нет репрезентативного набора данных. Для тестирования я взял выборку данных Метрики, Директа, Браузера и авиаперелётов в США. Но этого недостаточно: ClickHouse используется сотнями компаний по всему миру, и переоптимизировав его на одном наборе данных, мы можем не заметить падения производительности с другими данными. А если результаты зависят от модели процессора, придётся явно вписывать условия в код и тестировать его на каждой модели (либо смотреть справочные данные по таймингам инструкций — как считаете?). В любом случае это слишком трудоёмко.
Тогда я решил использовать другой метод, который очевиден для коллег, которые не зря учились в ШАДе. Это «многорукие бандиты». Суть в том, что вариант алгоритма выбирается случайным образом, а затем мы на основе статистики начинаем чаще выбирать те варианты, которые хорошо себя показали.
У нас есть много блоков данных, которые нужно разжать. То есть нужны независимые вызовы функции разжатия данных. Мы можем для каждого блока выбирать какой-нибудь из четырёх алгоритмов и измерять время его работы. Такая операция обычно ничего не стоит по сравнению с обработкой блока данных — а в ClickHouse блок несжатых данных составляет минимум 64 КБ. (Прочтите статью про измерение времени.)
Чтобы понять, как конкретно работает алгоритм «многорукие бандиты», узнаем, почему он так называется. Это аналогия с автоматами в казино, у которых есть несколько ручек, которые можно дёрнуть, чтобы получить какое-то случайное количество денег. Игрок может много раз дёргать ручки в любой выбираемой им последовательности. У каждой ручки есть фиксированное соответствующее ей вероятностное распределение количества выдаваемых денег, но игрок его не знает и может лишь оценить его, исходя из опыта игры. Тогда он сумеет максимизировать свою выгоду.
Один из подходов к максимизации выигрыша состоит в том, чтобы на каждом шаге оценивать вероятностное распределение для каждой ручки, исходя из статистики игры на предыдущих шагах. Затем в уме «разыгрываем» случайный выигрыш для каждой ручки, основываясь на полученных распределениях. И затем дёргаем ту ручку, для которой разыгранный в уме исход оказался лучше. Этот подход называется Thompson Sampling.
Мы, в свою очередь, должны выбрать алгоритм разжатия. Результат — время работы в пикосекундах на байт: чем меньше, тем лучше. Будем считать время работы случайной величиной и оценивать её распределение. Чтобы оценивать распределение случайной величины, надо использовать методы математической статистики. Для таких задач часто используют байесовский подход, но было бы неэффективно вписывать сложные формулы в код на C++. Можно использовать параметрический подход — сказать, что случайная величина принадлежит какому-то семейству случайных величин, зависящих от параметров; и затем оценивать эти параметры.
Как выбрать семейство случайных величин? Для примера мы могли бы считать, что время выполнения кода имеет нормальное распределение. Но это абсолютно неверно. Во-первых, время выполнения не может быть отрицательным, а нормальное распределение принимает значения на всей числовой прямой. Во-вторых, время выполнения, как я предполагаю, имеет большой «хвост» справа.
Впрочем, есть факторы, исходя из которых использовать оценку нормального распределения лишь для целей Thompson Sampling — неплохая идея (даже несмотря на то, что распределение искомой величины заведомо не является нормальным). Причина в том, что необходимая оценка матожидания и дисперсии выполняется очень просто, а после достаточного количества итераций нормальное распределение станет более-менее узким, не сильно отличающимся от распределений, которые мы бы получили другими методами. Если нас не очень сильно интересует скорость сходимости на первых шагах, то такими деталями можно пренебречь.
С одной стороны, это несколько «невежественный» подход. Из опыта известно, что среднее время выполнения запроса, загрузки сайта и так далее представляет собой «мусор», который не имеет смысла вычислять. Лучше было бы вычислять медиану — робастную статистику. Но это несколько сложнее, и как я покажу дальше, для практических целей описанный метод себя оправдывает.
Сначала я реализовал расчёт матожидания и дисперсии, а потом решил, что это слишком хорошо, и нужно упростить код, чтобы получилось «хуже»:
Я написал всё так, чтобы первые несколько итераций не учитывались — чтобы исключить эффект memory latencies.
Получилась тестовая программа, которая умеет сама подбирать лучший алгоритм на входных данных, а в качестве дополнительных режимов работы — использовать референсную реализацию LZ4 либо фиксированный вариант алгоритма.
Таким образом, есть шесть вариантов работы:
— reference (baseline): оригинальный LZ4 без наших модификаций;
— variant 0: копировать по 8 байт, не использовать shuffle;
— variant 1: копировать по 8 байт, использовать shuffle;
— variant 2: копировать по 16 байт, не использовать shuffle;
— variant 3: копировать по 16 байт, использовать shuffle;
— «бандитский» вариант, который сам во время работы выбирает лучший из четырёх перечисленных оптимизированных вариантов.
Если результат сильно зависит от модели CPU, было бы любопытно изучить, как именно. Может быть, на некоторых CPU разница особенно большая?
Я подготовил набор датасетов из разных таблиц в ClickHouse с реальными данными, всего 256 разных файлов по 100 МБ несжатых данных (число 256 просто совпало). И посмотрел, какие CPU у серверов, на которых я могу запустить бенчмарки. Я нашёл серверы с такими CPU:
— Intel® Xeon® CPU E5-2650 v2 @ 2.60GHz
— Intel® Xeon® CPU E5-2660 v4 @ 2.00GHz
— Intel® Xeon® CPU E5-2660 0 @ 2.20GHz
— Intel® Xeon® CPU E5645 @ 2.40GHz
— Intel Xeon E312xx (Sandy Bridge)
— AMD Opteron(TM) Processor 6274
— AMD Opteron(tm) Processor 6380
— Intel® Xeon® CPU E5-2683 v4 @ 2.10GHz
— Intel® Xeon® CPU E5530 @ 2.40GHz
— Intel® Xeon® CPU E5440 @ 2.83GHz
— Intel® Xeon® CPU E5-2667 v2 @ 3.30GHz
Дальше самое интересное — процессоры, предоставленные отделом R&D:
— AMD EPYC 7351 16-Core Processor — новый серверный процессор AMD.
— Cavium ThunderX2 — а это вообще не x86, а AArch64. Для них мои SIMD-оптимизации потребовалось немного переделывать. На сервере определяется 224 логических и 56 физических ядер.
Всего 13 серверов, на каждом из которых запускается тест на 256 файлах в 6 вариантах (reference, 0, 1, 2, 3, adaptive), причём тест запускаем 10 раз, чередуя варианты вперемешку. Получается 199 680 результатов, и их можно сравнивать.
Например, можно сравнить разные CPU между собой. Но не стоит делать поспешные выводы из этих результатов: мы тестируем только алгоритм разжатия LZ4 на одном ядре (очень узкий кейс — получается микробенчмарк). К примеру, у Cavium самое слабое ядро. Но я тестировал на нём сам ClickHouse, и он «рвёт» Xeon E5-2650 v2 на тяжёлых запросах за счёт превосходства по количеству ядер, даже несмотря на отсутствие многих оптимизаций, которые в ClickHouse делаются только для x86.
ref, adapt, max — это скорость в гигабайтах в секунду (величина, обратная к среднему арифметическому времени по всем запускам на всех наборах данных). best — номер лучшего алгоритма среди оптимизированных вариантов, от 0 до 3. adapt_boost — относительное преимущество адаптивного алгоритма по сравнению с baseline. max_boost — относительное преимущество лучшего из неадаптивных вариантов по сравнению с baseline. adapt_over_max — относительное преимущество адаптивного алгоритма по сравнению с лучшим неадаптивным.
Как видно, на современных процессорах x86 мы смогли ускорить разжатие на 12–20%. Даже на ARM мы получили плюс 4%, несмотря на то, что мы уделили меньше внимания оптимизации под эту архитектуру. Также заметно, что в среднем по разным наборам данных «бандитский» алгоритм выигрывает у выбранного наперёд лучшего варианта на всех процессорах кроме очень старых Intel.
На практике проделанная работа имеет сомнительную полезность. Да, само разжатие LZ4 ускорилось в среднем на 12–20%, а на отдельных наборах данных есть даже более чем двухкратный прирост производительности. Но в целом на время выполнения запроса это влияет существенно меньше. Не так легко найти настоящие запросы, на которых преимущество в скорости будет более пары процентов.
Стоит иметь в виду, что на нескольких кластерах Метрики, предназначенных для выполнения «длинных» запросов, мы решили использовать ZStandard level 1 вместо LZ4: на холодных данных важнее экономить IO и место на дисках.
Наибольшие преимущества от оптимизации разжатия наблюдаются на сильно сжимающихся данных — например, на столбцах с повторяющимися строковыми значениями. Но специально для этого сценария у нас разработано отдельное решение, которое позволяет ускорить такие запросы на порядки.
Ещё одно полезное соображение: оптимизация скорости алгоритма сжатия часто ограничена форматом сжатых данных. LZ4 использует очень хороший формат, но у Lizard, Density и LZSSE другие форматы, которые могут работать быстрее. Возможно, вместо попыток ускорить LZ4 было бы лучше просто подключить LZSSE к ClickHouse.
Внедрение этих оптимизаций в саму библиотеку LZ4 маловероятно: для их использования нужно изменить или дополнить интерфейс библиотеки. На самом деле это очень частый случай при улучшении алгоритмов: оптимизации не укладываются в старые абстракции, требуют их пересмотра. В то же время в оригинальной имплементации уже сейчас исправлено довольно много названий. Например, в части inc- и dec-таблиц теперь всё правильно. Кроме того, несколько недель назад оригинальная имплементация ускорила разжатие на те же 12–15% с помощью копирования по 32 байта, а не по 16, как указано выше. Мы и сами пробовали вариант с 32 байтами — результаты получились не такими классными, но в целом ускорение тоже есть.
Если посмотреть на профиль в начале статьи, можно заметить, что мы могли бы убрать одно лишнее копирование из page cache в userspace (либо с помощью mmap, либо с помощью O_DIRECT и userspace page cache — оба варианта сопряжены с проблемами), а также немного улучшить вычисление чек-сумм (сейчас используется CityHash128 без CRC32-C, а можно взять HighwayHash, FARSH или XXH3). Ускорение этих двух операций полезно для слабо сжимающихся данных, так как они производятся над сжатыми данными.
В любом случае, изменения уже добавлены в master, а полученные в результате этого исследования идеи нашли применение в других задачах. Вот видео с HighLoad++ Siberia, а вот презентация.
Данные в ClickHouse хранятся в сжатом виде. А во время выполнения запросов ClickHouse старается почти ничего не делать — использовать минимум ресурсов CPU. Бывает, что все вычисления, на которые могло тратиться время, уже хорошо оптимизированы, да и запрос хорошо написан пользователем. Тогда остаётся выполнить разжатие.
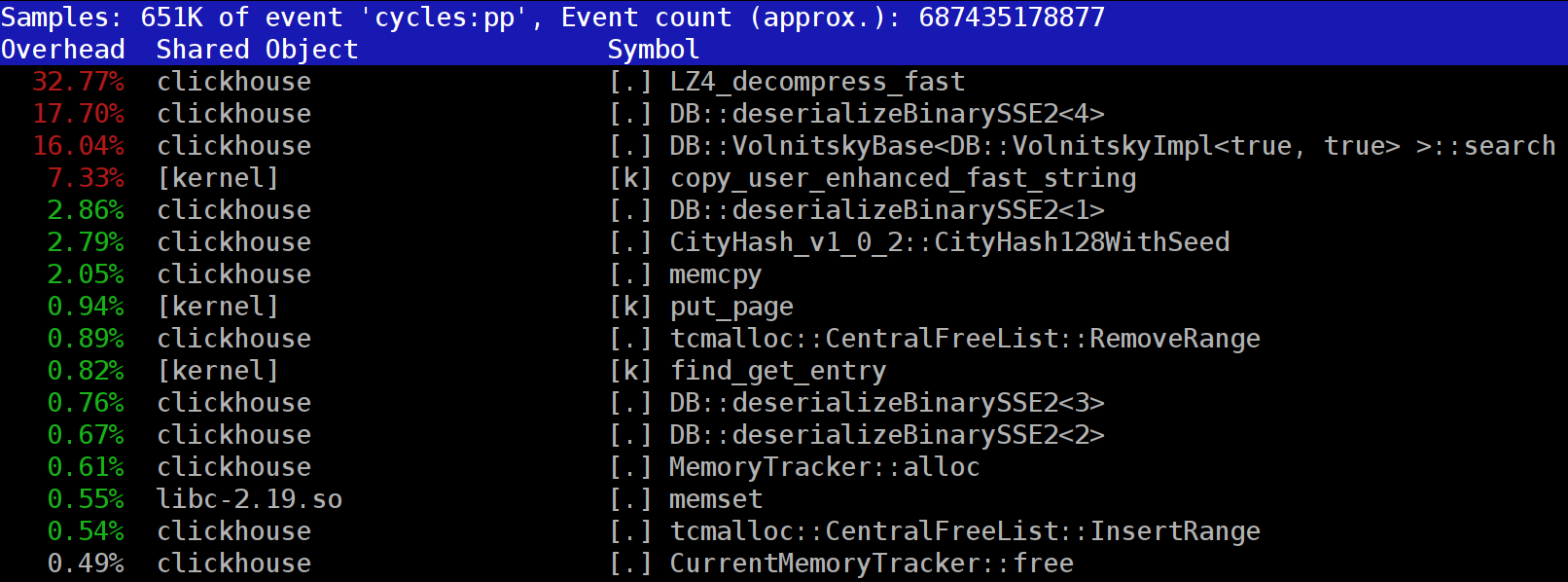
Вопрос — почему разжатие LZ4 может быть узким местом? Казалось бы, LZ4 — очень лёгкий алгоритм: скорость разжатия, в зависимости от данных, обычно составляет от 1 до 3 ГБ/с на одно процессорное ядро. Это уже существенно больше скорости работы дисковой подсистемы. Более того, мы используем все доступные ядра, а разжатие линейно масштабируется по всем физическим ядрам.
Но следует иметь в виду два момента. Во-первых, с диска читаются сжатые данные, а скорость разжатия приведена в количестве несжатых данных. Если коэффициент сжатия достаточно большой, то с дисков почти ничего не надо считывать. Но при этом разжатых данных образуется много, и разумеется, это влияет на расход CPU: объём работы по разжатию данных в случае LZ4 почти пропорционален объёму самих разжатых данных.
Во-вторых, чтение данных с дисков может не требоваться вообще, если данные находятся в кэше. Для этого можно полагаться на page cache или использовать свой собственный кэш. В столбцовых БД использование кэша более эффективно за счёт того, что в него попадают не все столбцы, а только часто используемые. Вот почему LZ4 в смысле нагрузки на CPU часто является узким местом.
Отсюда ещё два вопроса. Если разжатие данных «тормозит», то может, их вообще не стоит сжимать? Но на практике это предположение бессмысленно. Недавно в ClickHouse можно было настроить всего два варианта сжатия данных — LZ4 и Zstandard. По умолчанию используется LZ4. Переключившись на Zstandard, можно сделать сжатие сильнее и медленнее. А вот полностью отключить сжатие ещё совсем недавно было нельзя — LZ4 рассматривается как разумный минимум, который можно использовать всегда. Именно поэтому я очень люблю LZ4. :)
Но недавно в англоязычном чате поддержки ClickHouse появился таинственный незнакомец, который рассказал, что у него очень быстрая дисковая подсистема (NVMe SSD) и всё упирается в сжатие — неплохо было бы иметь возможность его выключить. Я ответил, что такой возможности нет, но её легко добавить. Через несколько дней нам пришёл пул-реквест, в котором реализуется метод сжатия
none. Я попросил привести результаты — насколько это помогло, насколько ускорились запросы. Человек сказал, что эта новая фича оказалась бесполезной на практике, поскольку данные без сжатия стали занимать слишком много места.Второй возникающий вопрос: если есть кэш, почему бы не хранить в нём уже разжатые данные? Это допускается — во многих случаях так удастся избавиться от необходимости разжатия. И в ClickHouse есть такой кэш — кэш разжатых блоков. Но на него жалко тратить много оперативки из-за его низкой эффективности. Он оправдывает себя только на мелких, идущих подряд запросах, которые используют почти одни и те же данные.
Общее соображение: данные надо сжимать, желательно всегда. Всегда записывайте их на диск со сжатием. Передавайте по сети тоже со сжатием. На мой взгляд, сжатие по умолчанию следует считать оправданным даже при передаче в 10-гигабитной сети без переподписки в пределах дата-центра, а передавать данные без сжатия между дата-центрами вообще недопустимо.
Почему именно LZ4
Почему же используется именно LZ4? Можно ли подобрать нечто ещё более лёгкое? В принципе, можно, и это правильно и полезно. Но давайте сначала рассмотрим, к какому классу алгоритмов относится LZ4.
Во-первых, он не зависит от типа данных. К примеру, если вы заранее знаете, что у вас будет массив целых чисел, то можете использовать один из многочисленных вариантов алгоритма VarInt — так будет эффективнее по CPU. Во-вторых, LZ4 не слишком сильно зависит от требуемых допущений на модель данных. Предположим, у вас есть упорядоченный временной ряд показаний датчика — массив с числами типа float. Тогда вы можете посчитать дельты, а затем сжимать дальше, и это будет эффективнее по коэффициенту сжатия.
То есть LZ4 можно без проблем использовать для любых массивов байтов — для любых файлов. Конечно, у него есть своя специализация (об этом ниже), и в некоторых случаях его использование бессмысленно. Но если его назвать алгоритмом общего назначения, это будет небольшой ошибкой. И заметим, что, благодаря внутреннему устройству, LZ4 в качестве частного случая автоматом реализует алгоритм RLE.
Другой вопрос: неужели LZ4 — наиболее оптимальный алгоритм данного класса по совокупности скорости и силы сжатия? Такие алгоритмы называются pareto frontier — это значит, что не существует другого алгоритма, который строго лучше по одному показателю и не хуже по другим (да ещё и на широком множестве датасетов). Есть алгоритмы, которые быстрее, но дают меньший коэффициент сжатия, а есть те, которые сжимают сильнее, но при этом медленнее сжимают или разжимают.
На самом деле LZ4 — не pareto frontier. Есть варианты, которые чуть-чуть лучше. Например, это LZTURBO от некоего powturbo. В достоверности результатов можно не сомневаться благодаря сообществу на encode.ru (крупнейшем и примерно единственном форуме по сжатию данных). Но разработчик не распространяет ни исходники, ни бинарники, а только даёт их ограниченному кругу лиц для тестирования или за кучу денег (вроде никто до сих пор не заплатил). Также стоит обратить внимание на Lizard (бывший LZ5) и Density. Они могут работать чуть лучше LZ4 при выборе некоторого уровня сжатия. Также обратите внимание на LZSSE — крайне интересная вещь. Впрочем, посмотреть на неё лучше после прочтения этой статьи.
Как работает LZ4
Давайте рассмотрим, как вообще работает LZ4. Это одна из реализаций алгоритма LZ77: L и Z указывают на фамилии авторов (Лемпель и Зив), а 77 — на 1977 год, когда алгоритм был опубликован. У него множество других реализаций: QuickLZ, FastLZ, BriefLZ, LZF, LZO, а также gzip и zip в случае использования низких уровней сжатия.
Сжатый с помощью LZ4 блок данных содержит последовательность записей (команд, инструкций) двух видов:
- Литерал (literals): «возьми следующие N байт как есть и скопируй их в результат».
- Матч (match, совпадение): «возьми N байт, которые уже были в разжатом результате по смещению offset от текущей позиции».
Пример. До сжатия:
Hello world HelloПосле сжатия:
literals 12 "Hello world " match 5 12Если взять сжатый блок и пройтись по нему курсором, выполняя эти команды, то мы получим в качестве результата исходные, разжатые данные.
Мы примерно рассмотрели, как данные разжимаются. Также ясна суть: для выполнения сжатия алгоритм кодирует повторяющиеся последовательности байт с помощью матчей.
Ясны и некоторые свойства. Этот алгоритм byte-oriented — он не препарирует отдельные байты, а лишь копирует их целиком. Здесь кроется отличие, например, от энтропийного кодирования. Для примера, zstd является композицией LZ77 и энтропийного кодирования.
Заметим, что размер сжатого блока выбирается не слишком большим, чтобы не тратить много оперативки во время разжатия; чтобы не сильно замедлить random access в сжатом файле (который состоит из множества сжатых блоков); и иногда — чтобы блок помещался в какой-нибудь кэш CPU. Например, можно выбрать 64 КБ — так буферы для сжатых и несжатых данных поместятся в L2-кэш и половина ещё останется.
Если нам потребуется сжать файл большего размера, мы просто будем конкатенировать сжатые блоки. Заодно рядом с каждым сжатым блоком удобно расположить дополнительные данные — размеры, чек-сумму.
Максимальное смещение для матча ограничено, в LZ4 — 64 килобайтами. Эта величина называется sliding window. Действительно, это значит, что по мере продвижения курсора вперёд совпадения могут находиться в окне размером 64 килобайта до курсора, которое движется вместе с курсором.
Теперь рассмотрим, как сжать данные — другими словами, как найти в файле совпадающие последовательности. Конечно, вы можете использовать suffix trie (классно, если вы о нём слышали). Есть варианты, при которых в процессе сжатия среди предыдущих байт гарантированно находится самая длинная совпадающая последовательность. Это называется optimal parsing и даёт почти лучший коэффициент сжатия для фиксированного формата сжатого блока. Но есть и более эффективные варианты — когда мы находим какое-нибудь достаточно хорошее совпадение в данных, но не обязательно самое длинное. Самый эффективный способ его найти — использовать хэш-таблицу.
Для этого проходимся по исходному блоку данных курсором и берём несколько байт после курсора. Например, 4 байта. Хэшируем их и кладём в хэш-таблицу смещение от начала блока — где эти 4 байта встретились. Величина 4 называется min-match — с помощью такой хэш-таблицы мы можем отыскать совпадения минимум в 4 байта.
Если мы посмотрели в хэш-таблицу, а там уже есть запись, и если смещение не превышает sliding window, то мы проверяем, сколько ещё байт совпадает после этих четырёх байт. Может быть, там ещё много чего совпадает. Возможно и такое, что в хэш-таблице возникла коллизия и не совпадает ничего. Это нормально — можно просто заменить значение в хэш-таблице на новое. Коллизии в хэш-таблице будут просто приводить к меньшему коэффициенту сжатия, поскольку найдётся меньше совпадений. Кстати, такой вид хэш-таблиц (фиксированного размера и без разрешения коллизий) называется cache table, кэш-таблица. Это тоже логично — в случае коллизии кэш-таблица просто забывает про старую запись.
Задача для внимательного читателя. Пусть данные — это массив чисел типа UInt32 в формате little endian, представляющий собой часть последовательности натуральных чисел: 0, 1, 2… Объясните, почему при использовании LZ4 эти данные не сжимаются (объём сжатых данных оказывается не меньше, чем объём несжатых данных).
Как всё ускорить
Итак, я хочу ускорить разжатие LZ4. Давайте посмотрим, что из себя представляет цикл разжатия. Вот этот цикл в псевдокоде:
while (...)
{
read(input_pos, literal_length, match_length);
copy(output_pos, input_pos, literal_length);
output_pos += literal_length;
read(input_pos, match_offset);
copy(output_pos, output_pos - match_offset,
match_length);
output_pos += match_length;
}Формат LZ4 устроен так, что в сжатом файле литералы и матчи чередуются. И очевидно, первым всегда идёт literal (потому что с самого начала матч ещё неоткуда взять). Поэтому их длины кодируются вместе.
На самом деле всё чуть-чуть сложнее. Из файла читается один байт, и из него берутся две половинки (nibble), в которых закодированы числа от 0 до 15. Если соответствующее число не равно 15, то оно считается длиной литерала и матча соответственно. А если оно равно 15, то длина больше и она закодирована в следующих байтах. Тогда считывается следующий байт, и его значение прибавляется к длине. Далее, если оно равно 255, то мы продолжаем — считываем следующий байт так же.
Отметим, что максимальный коэффициент сжатия для формата LZ4 не достигает 255. И второе (бесполезное) наблюдение: если ваши данные очень избыточны, то применение LZ4 дважды позволит увеличить коэффициент сжатия.
Когда мы прочитали длину литерала (а затем так же — длину матча и смещение матча), для разжатия достаточно просто скопировать два фрагмента памяти.
Как копировать фрагмент памяти
Казалось бы, можно использовать функцию
memcpy, которая как раз предназначена для копирования фрагментов памяти. Но это неоптимально и всё-таки некорректно.Почему использовать функцию memcpy неоптимально? Потому что она:
- обычно находится в библиотеке libc (а библиотека libc обычно линкуется динамически, и вызов memcpy будет идти косвенно, через PLT),
- не инлайнится с неизвестным в compile time аргументом size,
- делает много усилий для корректной обработки «хвостов» фрагмента памяти, не кратных размеру машинного слова или регистра.
Последний пункт самый важный. Допустим, мы попросили функцию memcpy скопировать ровно 5 байт. Было бы очень хорошо скопировать сразу 8 байт, использовав для этого две инструкции movq.
Hello world Hello wo...
^^^^^^^^ - src
^^^^^^^^ - dstНо тогда мы скопируем три лишних байта — то есть будем писать за границу переданного буфера. Функция
memcpy не имеет права это делать — действительно, ведь так мы перезапишем какие-то данные в нашей программе, будет «проезд» по памяти. А если мы писали по невыровненному адресу, то эти лишние байты могут быть расположены на невыделенной странице виртуальной памяти или на странице без доступа на запись. Тогда мы получим segfault (это хорошо).Но в нашем случае мы почти всегда можем писать лишние байты. Можем считывать лишние байты в input-буфере до тех пор, пока лишние байты расположены в нём целиком. При тех же условиях мы можем записать лишние байты в output-буфер — потому что на следующей итерации мы их всё равно перезапишем.
Эта оптимизация уже есть в оригинальной реализации LZ4:
inline void copy8(UInt8 * dst, const UInt8 * src)
{
memcpy(dst, src, 8); /// На самом деле здесь memcpy не вызывается.
}
inline void wildCopy8(UInt8 * dst, const UInt8 * src, UInt8 * dst_end)
{
do
{
copy8(dst, src);
dst += 8;
src += 8;
} while (dst < dst_end);
}Чтобы воспользоваться такой оптимизацией, нужно лишь проверять, что мы находимся достаточно далеко от границы буфера. Это должно быть бесплатно, потому что мы и так проверяем выход за границы буфера. А обработку последних нескольких байт — «хвостика» данных — можно делать уже после основного цикла.
Впрочем, всё равно есть некоторые тонкости. В цикле два копирования — литерала и матча. Но при использовании функции LZ4_decompress_fast (вместо LZ4_decompress_safe) проверка выполняется один раз — когда нам нужно скопировать литерал. При копировании матча проверка не выполняется, но в самой спецификации формата LZ4 есть условия, которые позволяют её избежать:
The last 5 bytes are always literals
The last match must start at least 12 bytes before end of block.
Consequently, a block with less than 13 bytes cannot be compressed.
Специально подобранные входные данные могут вызвать «проезд» по памяти. Если вы используете функцию LZ4_decompress_fast, вам нужна защита от плохих данных. Сжатые данные надо по крайней мере чек-суммировать. А если вам нужна защита от злоумышленника, то используйте функцию LZ4_decompress_safe. Другие варианты: берите криптографическую хэш-функцию в качестве чек-суммы, но это почти наверное убьёт всю производительность; либо выделяйте больше памяти для буферов; либо выделяйте память для буферов отдельным вызовом mmap и создайте guard page.
Когда я вижу код, который копирует данные по 8 байт, сразу спрашиваю — а почему именно по 8 байт? Можно копировать по 16 байт, используя SSE-регистры:
inline void copy16(UInt8 * dst, const UInt8 * src)
{
#if __SSE2__
_mm_storeu_si128(reinterpret_cast<__m128i *>(dst),
_mm_loadu_si128(reinterpret_cast<const __m128i *>(src)));
#else
memcpy(dst, src, 16);
#endif
}
inline void wildCopy16(UInt8 * dst, const UInt8 * src, UInt8 * dst_end)
{
do
{
copy16(dst, src);
dst += 16;
src += 16;
} while (dst < dst_end);
}Аналогично работает копирование 32 байт для AVX и 64 байт для AVX-512. Кроме того, можно развернуть цикл в несколько раз. Если вы когда-нибудь смотрели, как реализована
memcpy, то в ней именно такой подход. (Кстати, компилятор в данном случае не будет ни разворачивать, ни векторизовывать цикл: это потребует вставки громоздких проверок.) Почему в оригинальной реализации LZ4 так не сделано? Во-первых, неочевидно, лучше это или хуже. Результат зависит от размеров фрагментов, которые нужно копировать. Вдруг они все короткие и лишняя работа будет ни к чему? А во-вторых, это рушит те условия в формате LZ4, которые позволяют избежать лишнего бранча во внутреннем цикле.
Тем не менее, будем пока держать этот вариант в уме.
Хитрые копирования
Вернёмся к вопросу — всегда ли можно таким образом копировать данные? Предположим, нам нужно скопировать матч — то есть скопировать фрагмент памяти из output-буфера, находящийся на некотором смещении позади от курсора, в позицию этого курсора.
Представим простой случай — нужно скопировать 5 байт по смещению 12:
Hello world ...........
^^^^^ - src
^^^^^ - dst
Hello world Hello wo...
^^^^^ - src
^^^^^ - dstНо есть более сложный случай — когда нам нужно скопировать фрагмент памяти, длина которого больше смещения. То есть он частично указывает на данные, которые ещё не были записаны в output-буфер.
Копируем 10 байт по смещению 3:
abc.............
^^^^^^^^^^ - src
^^^^^^^^^^ - dst
abcabcabcabca...
^^^^^^^^^^ - src
^^^^^^^^^^ - dstВ процессе сжатия у нас есть все данные, и такой матч вполне может найтись. Функция
memcpy не подходит для того, чтобы его скопировать: она не поддерживает случай, когда диапазоны фрагментов памяти пересекаются. Кстати, функция memmove тоже не подходит, потому что фрагмент памяти, откуда нужно брать данные, ещё не полностью инициализирован. Копировать нужно так же, как если бы мы копировали побайтово.op[0] = match[0]; op[1] = match[1]; op[2] = match[2]; op[3] = match[3]; ...
Вот как это работает:
abca............
^ - src
^ - dst
abcab...........
^ - src
^ - dst
abcabc..........
^ - src
^ - dst
abcabca.........
^ - src
^ - dst
abcabcab........
^ - src
^ - dstТо есть мы должны создать повторяющуюся последовательность. В оригинальной реализации LZ4 для этого написан удивительно непонятный код:
const unsigned dec32table[] = {0, 1, 2, 1, 4, 4, 4, 4};
const int dec64table[] = {0, 0, 0, -1, 0, 1, 2, 3};
const int dec64 = dec64table[offset];
op[0] = match[0];
op[1] = match[1];
op[2] = match[2];
op[3] = match[3];
match += dec32table[offset];
memcpy(op+4, match, 4);
match -= dec64;Мы копируем первые 4 байта побайтово, смещаемся на какое-то магическое число, копируем следующие 4 байта целиком, смещаем указатель на match на другое магическое число. Автор кода (Ян Коллет) по какой-то нелепой причине забыл оставить комментарий, что это значит. К тому же имена переменных запутывают. Обе называются dec...table, но одну из них мы прибавляем, а другую — вычитаем. Кроме того, ещё одна из них имеет тип unsigned, а другая — int. Впрочем, стоит отдать должное: как раз недавно автор улучшил это место в коде.
Вот как на самом деле это работает. Копируем первые 4 байта побайтово:
abcabca.........
^^^^ - src
^^^^ - dstТеперь можно скопировать 4 байта сразу:
abcabcabcab.....
^^^^ - src
^^^^ - dstМожно продолжить как обычно, копируя 8 байт сразу:
abcabcabcabcabcabca.....
^^^^^^^^ - src
^^^^^^^^ - dstКак вы знаете из опыта, иногда лучший способ понять код — это переписать его. Вот что получилось:
inline void copyOverlap8(UInt8 * op, const UInt8 *& match, const size_t offset)
{
/// 4 % n.
/// Or if 4 % n is zero, we use n.
/// It gives equivalent result, but is better CPU friendly for unknown reason.
static constexpr int shift1[] = { 0, 1, 2, 1, 4, 4, 4, 4 };
/// 8 % n - 4 % n
static constexpr int shift2[] = { 0, 0, 0, 1, 0, -1, -2, -3 };
op[0] = match[0];
op[1] = match[1];
op[2] = match[2];
op[3] = match[3];
match += shift1[offset];
memcpy(op + 4, match, 4);
match += shift2[offset];
}Производительность, конечно же, не изменилась никак. Впрочем, я очень хотел попробовать оптимизацию, в которой обычное копирование — сразу по 16 байт.
Но это усложняет «особый случай» и приводит к тому, что он вызывается чаще (условие
offset < 16 выполнено не реже, чем offset < 8). Копирование (начала) пересекающихся диапазонов для случая 16-байтных копирований выглядит так:inline void copyOverlap16(UInt8 * op, const UInt8 *& match, const size_t offset)
{
/// 4 % n.
static constexpr int shift1[]
= { 0, 1, 2, 1, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4 };
/// 8 % n - 4 % n
static constexpr int shift2[]
= { 0, 0, 0, 1, 0, -1, -2, -3, -4, 4, 4, 4, 4, 4, 4, 4 };
/// 16 % n - 8 % n
static constexpr int shift3[]
= { 0, 0, 0, -1, 0, -2, 2, 1, 8, -1, -2, -3, -4, -5, -6, -7 };
op[0] = match[0];
op[1] = match[1];
op[2] = match[2];
op[3] = match[3];
match += shift1[offset];
memcpy(op + 4, match, 4);
match += shift2[offset];
memcpy(op + 8, match, 8);
match += shift3[offset];
}Можно ли реализовать именно эту функцию оптимальнее? Хотелось бы, чтобы для такого сложного кода нашлась магическая SIMD-инструкция, ведь мы всего лишь хотим записать 16 байт, которые целиком состоят из нескольких байт входных данных (от 1 до 15). Их, в свою очередь, нужно просто повторить в правильном порядке.
Такая инструкция есть — она называется
pshufb (от слов packed shuffle bytes) и входит в SSSE3 (три буквы S). Она принимает два 16-байтных регистра. В одном регистре содержатся исходные данные. В другом — «селектор»: в каждом байте записано число от 0 до 15 — в зависимости от того, из какого байта исходного регистра взять результат. Или, если значение байта селектора больше 127 — заполнить соответствующий байт результата нулём.Вот пример:
xmm0: abc............. xmm1: 0120120120120120 pshufb %xmm1, %xmm0 xmm0: abcabcabcabcabca
Каждый байт результата мы заполнили выбранным нами байтом исходных данных — это как раз то что надо! Вот как выглядит код в результате:
inline void copyOverlap16Shuffle(UInt8 * op, const UInt8 *& match, const size_t offset)
{
#ifdef __SSSE3__
static constexpr UInt8 __attribute__((__aligned__(16))) masks[] =
{
0, 1, 2, 1, 4, 1, 4, 2, 8, 7, 6, 5, 4, 3, 2, 1, /* offset = 0, not used as mask, but for shift amount instead */
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, /* offset = 1 */
0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1,
0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0, 1, 2, 0,
0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3,
0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0,
0, 1, 2, 3, 4, 5, 0, 1, 2, 3, 4, 5, 0, 1, 2, 3,
0, 1, 2, 3, 4, 5, 6, 0, 1, 2, 3, 4, 5, 6, 0, 1,
0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, 3, 4, 5, 6, 7,
0, 1, 2, 3, 4, 5, 6, 7, 8, 0, 1, 2, 3, 4, 5, 6,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4, 5,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3, 4,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 0, 1, 2,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 0, 1,
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 0,
};
_mm_storeu_si128(reinterpret_cast<__m128i *>(op),
_mm_shuffle_epi8(
_mm_loadu_si128(reinterpret_cast<const __m128i *>(match)),
_mm_load_si128(reinterpret_cast<const __m128i *>(masks) + offset)));
match += masks[offset];
#else
copyOverlap16(op, match, offset);
#endif
}Здесь
_mm_shuffle_epi8 — это intrinsic, разворачивающийся в инструкцию pshufb.Можно ли сделать такую операцию для большего числа байт сразу, используя более новые инструкции? Ведь SSSE3 — очень старый набор инструкций, существующий с 2006 года. В AVX2 есть инструкция, которая делает это сразу для 32 байт, но только независимо для отдельных 16-байтных фрагментов. Она называется уже не packed shuffle bytes, а vector permute bytes — слова другие, а смысл такой же. В AVX-512 VBMI есть ещё одна инструкция, работающая сразу для 64 байт, но процессоры с её поддержкой появились совсем недавно. Похожие инструкции также есть в ARM NEON — они называются vtbl (vector table lookup), но позволяют записывать только 8 байт.
Кроме того, существует вариант инструкции
pshufb с 64-битными MMX-регистрами, чтобы сформировать 8 байт. Он как раз подходит для замены исходного варианта кода. Правда, вместо неё я решил всё равно использовать вариант, работающий с 16 байтами (по серьёзным причинам).На конференции Highload++ Siberia после моего доклада ко мне подошёл слушатель и сказал, что для случая 8 байт можно просто использовать умножение на специально подобранную константу (также потребуется сдвиг) — я об этом раньше даже не думал!
Как убрать лишний if
Допустим, я хочу использовать вариант, копирующий по 16 байт. Как избежать необходимости дополнительной проверки выхода за границы буфера?
Я решил, что вообще не буду делать эту проверку. В комментарии к функции будет написано, что разработчику следует выделить кусок памяти на указанное количество байт больше, чем требуется, чтобы позволить нам читать и писать туда ненужный мусор. Интерфейс функции станет неудобным, но это уже другие проблемы.
Впрочем, могут возникнуть негативные последствия. Допустим, данные, которые нам надо разжимать, были сформированы из блоков по 65 536 байт. Тогда пользователь даёт нам фрагмент памяти размером 65 536 байт для разжатых данных. Но с новым интерфейсом функции пользователь будет обязан выделить фрагмент памяти, например, из 65 551 байта. Тогда аллокатор, вполне возможно, будет вынужден на самом деле выделить 96 или даже 128 килобайт — в зависимости от его реализации. Если же аллокатор очень плохой, он может внезапно перестать кэшировать фрагмент памяти у себя в «куче» и начать каждый раз использовать mmap для выделения памяти (либо освобождать память с помощью madvice). Такой процесс будет ужасно медленным из-за page faults. В итоге маленькая попытка оптимизации может привести к тому, что всё начнёт тормозить.
Есть ли ускорение?
Итак, я сделал вариант кода, в котором применены три оптимизации:
- Копируем по 16 байт вместо 8.
- Используются shuffle-инструкции для случая
offset < 16. - Убран один лишний if.
Я стал тестировать этот код на самых разных наборах данных и получил неожиданные результаты.
Пример 1:
Xeon E2650v2, данные Яндекс.Браузера, столбец AppVersion.
reference: 1.67 GB/sec.
16 bytes, shuffle: 2.94 GB/sec (на 76% быстрее).
Пример 2:
Xeon E2650v2, данные Яндекс.Директа, столбец ShowsSumPosition.
reference: 2.30 GB/sec.
16 bytes, shuffle: 1.91 GB/sec (на 20% медленнее).
Сначала я увидел, что всё ускорилось на десятки процентов и успел обрадоваться. Потом на других файлах увидел, что ничего не ускорилось. Ещё на каких-то замедлилось, хоть и ненамного. Я сделал вывод, что результаты зависят от коэффициента сжатия. Чем больше сжат файл — тем больше преимущество от перехода на 16 байт. Это естественно: чем больше коэффициент сжатия, тем больше средняя длина фрагментов, которые нужно копировать.
Чтобы лучше разобраться, я с помощью шаблонов C++ сделал варианты кода для четырёх случаев: оперируем 8- или 16- байтными кусочками; используем или не используем shuffle-инструкцию.
template <size_t copy_amount, bool use_shuffle>
void NO_INLINE decompressImpl(
const char * const source,
char * const dest,
size_t dest_size)На разных файлах выигрывали совершенно разные варианты кода, но при тестировании на рабочем компьютере вариант с shuffle всегда выигрывал. На рабочем компьютере тестировать неудобно, приходится делать так:
sudo echo 'performance' | tee /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor kill -STOP $(pidof firefox) $(pidof chromium)
Потом я пошёл на один из старых «разработческих» серверов (c процессором Xeon E5645), достал ещё больше наборов данных и получил почти диаметрально противоположные результаты, которые меня окончательно запутали. Выяснилось, что выбор оптимального алгоритма определяется не только коэффициентом сжатия, но и моделью процессора. От неё зависит то, когда лучше использовать shuffle-инструкцию, а также порог, начиная с которого лучше использовать 16-байтные копирования.
Кстати при тестировании на серверах имеет смысл делать так:
sudo kill -STOP $(pidof python) $(pidof perl) $(pgrep -u skynet) $(pidof cqudp-client)
Иначе результаты будут нестабильными. Также следите за thermal throttling и power capping.
Как выбрать лучший алгоритм
Итак, у нас есть четыре варианта алгоритма, и нужно в зависимости от условий выбирать лучший. Можно было бы создать репрезентативный набор данных и железа, затем провести хорошее нагрузочное тестирование и выбрать тот метод, который лучше в среднем. Но у нас нет репрезентативного набора данных. Для тестирования я взял выборку данных Метрики, Директа, Браузера и авиаперелётов в США. Но этого недостаточно: ClickHouse используется сотнями компаний по всему миру, и переоптимизировав его на одном наборе данных, мы можем не заметить падения производительности с другими данными. А если результаты зависят от модели процессора, придётся явно вписывать условия в код и тестировать его на каждой модели (либо смотреть справочные данные по таймингам инструкций — как считаете?). В любом случае это слишком трудоёмко.
Тогда я решил использовать другой метод, который очевиден для коллег, которые не зря учились в ШАДе. Это «многорукие бандиты». Суть в том, что вариант алгоритма выбирается случайным образом, а затем мы на основе статистики начинаем чаще выбирать те варианты, которые хорошо себя показали.
У нас есть много блоков данных, которые нужно разжать. То есть нужны независимые вызовы функции разжатия данных. Мы можем для каждого блока выбирать какой-нибудь из четырёх алгоритмов и измерять время его работы. Такая операция обычно ничего не стоит по сравнению с обработкой блока данных — а в ClickHouse блок несжатых данных составляет минимум 64 КБ. (Прочтите статью про измерение времени.)
Чтобы понять, как конкретно работает алгоритм «многорукие бандиты», узнаем, почему он так называется. Это аналогия с автоматами в казино, у которых есть несколько ручек, которые можно дёрнуть, чтобы получить какое-то случайное количество денег. Игрок может много раз дёргать ручки в любой выбираемой им последовательности. У каждой ручки есть фиксированное соответствующее ей вероятностное распределение количества выдаваемых денег, но игрок его не знает и может лишь оценить его, исходя из опыта игры. Тогда он сумеет максимизировать свою выгоду.
Один из подходов к максимизации выигрыша состоит в том, чтобы на каждом шаге оценивать вероятностное распределение для каждой ручки, исходя из статистики игры на предыдущих шагах. Затем в уме «разыгрываем» случайный выигрыш для каждой ручки, основываясь на полученных распределениях. И затем дёргаем ту ручку, для которой разыгранный в уме исход оказался лучше. Этот подход называется Thompson Sampling.
Мы, в свою очередь, должны выбрать алгоритм разжатия. Результат — время работы в пикосекундах на байт: чем меньше, тем лучше. Будем считать время работы случайной величиной и оценивать её распределение. Чтобы оценивать распределение случайной величины, надо использовать методы математической статистики. Для таких задач часто используют байесовский подход, но было бы неэффективно вписывать сложные формулы в код на C++. Можно использовать параметрический подход — сказать, что случайная величина принадлежит какому-то семейству случайных величин, зависящих от параметров; и затем оценивать эти параметры.
Как выбрать семейство случайных величин? Для примера мы могли бы считать, что время выполнения кода имеет нормальное распределение. Но это абсолютно неверно. Во-первых, время выполнения не может быть отрицательным, а нормальное распределение принимает значения на всей числовой прямой. Во-вторых, время выполнения, как я предполагаю, имеет большой «хвост» справа.
Впрочем, есть факторы, исходя из которых использовать оценку нормального распределения лишь для целей Thompson Sampling — неплохая идея (даже несмотря на то, что распределение искомой величины заведомо не является нормальным). Причина в том, что необходимая оценка матожидания и дисперсии выполняется очень просто, а после достаточного количества итераций нормальное распределение станет более-менее узким, не сильно отличающимся от распределений, которые мы бы получили другими методами. Если нас не очень сильно интересует скорость сходимости на первых шагах, то такими деталями можно пренебречь.
С одной стороны, это несколько «невежественный» подход. Из опыта известно, что среднее время выполнения запроса, загрузки сайта и так далее представляет собой «мусор», который не имеет смысла вычислять. Лучше было бы вычислять медиану — робастную статистику. Но это несколько сложнее, и как я покажу дальше, для практических целей описанный метод себя оправдывает.
Сначала я реализовал расчёт матожидания и дисперсии, а потом решил, что это слишком хорошо, и нужно упростить код, чтобы получилось «хуже»:
/// For better convergence, we don't use proper estimate of stddev.
/// We want to eventually separate between two algorithms even in case
/// when there is no statistical significant difference between them.
double sigma() const
{
return mean() / sqrt(adjustedCount());
}
double sample(pcg64 & rng) const
{
...
return std::normal_distribution<>(mean(), sigma())(rng);
}Я написал всё так, чтобы первые несколько итераций не учитывались — чтобы исключить эффект memory latencies.
Получилась тестовая программа, которая умеет сама подбирать лучший алгоритм на входных данных, а в качестве дополнительных режимов работы — использовать референсную реализацию LZ4 либо фиксированный вариант алгоритма.
Таким образом, есть шесть вариантов работы:
— reference (baseline): оригинальный LZ4 без наших модификаций;
— variant 0: копировать по 8 байт, не использовать shuffle;
— variant 1: копировать по 8 байт, использовать shuffle;
— variant 2: копировать по 16 байт, не использовать shuffle;
— variant 3: копировать по 16 байт, использовать shuffle;
— «бандитский» вариант, который сам во время работы выбирает лучший из четырёх перечисленных оптимизированных вариантов.
Тестирование на разных CPU
Если результат сильно зависит от модели CPU, было бы любопытно изучить, как именно. Может быть, на некоторых CPU разница особенно большая?
Я подготовил набор датасетов из разных таблиц в ClickHouse с реальными данными, всего 256 разных файлов по 100 МБ несжатых данных (число 256 просто совпало). И посмотрел, какие CPU у серверов, на которых я могу запустить бенчмарки. Я нашёл серверы с такими CPU:
— Intel® Xeon® CPU E5-2650 v2 @ 2.60GHz
— Intel® Xeon® CPU E5-2660 v4 @ 2.00GHz
— Intel® Xeon® CPU E5-2660 0 @ 2.20GHz
— Intel® Xeon® CPU E5645 @ 2.40GHz
— Intel Xeon E312xx (Sandy Bridge)
— AMD Opteron(TM) Processor 6274
— AMD Opteron(tm) Processor 6380
— Intel® Xeon® CPU E5-2683 v4 @ 2.10GHz
— Intel® Xeon® CPU E5530 @ 2.40GHz
— Intel® Xeon® CPU E5440 @ 2.83GHz
— Intel® Xeon® CPU E5-2667 v2 @ 3.30GHz
Дальше самое интересное — процессоры, предоставленные отделом R&D:
— AMD EPYC 7351 16-Core Processor — новый серверный процессор AMD.
— Cavium ThunderX2 — а это вообще не x86, а AArch64. Для них мои SIMD-оптимизации потребовалось немного переделывать. На сервере определяется 224 логических и 56 физических ядер.
Всего 13 серверов, на каждом из которых запускается тест на 256 файлах в 6 вариантах (reference, 0, 1, 2, 3, adaptive), причём тест запускаем 10 раз, чередуя варианты вперемешку. Получается 199 680 результатов, и их можно сравнивать.
Например, можно сравнить разные CPU между собой. Но не стоит делать поспешные выводы из этих результатов: мы тестируем только алгоритм разжатия LZ4 на одном ядре (очень узкий кейс — получается микробенчмарк). К примеру, у Cavium самое слабое ядро. Но я тестировал на нём сам ClickHouse, и он «рвёт» Xeon E5-2650 v2 на тяжёлых запросах за счёт превосходства по количеству ядер, даже несмотря на отсутствие многих оптимизаций, которые в ClickHouse делаются только для x86.
┌─cpu───────────────────┬──ref─┬─adapt─┬──max─┬─best─┬─adapt_boost─┬─max_boost─┬─adapt_over_max─┐ │ E5-2667 v2 @ 3.30GHz │ 2.81 │ 3.19 │ 3.15 │ 3 │ 1.14 │ 1.12 │ 1.01 │ │ E5-2650 v2 @ 2.60GHz │ 2.5 │ 2.84 │ 2.81 │ 3 │ 1.14 │ 1.12 │ 1.01 │ │ E5-2683 v4 @ 2.10GHz │ 2.26 │ 2.63 │ 2.59 │ 3 │ 1.16 │ 1.15 │ 1.02 │ │ E5-2660 v4 @ 2.00GHz │ 2.15 │ 2.49 │ 2.46 │ 3 │ 1.16 │ 1.14 │ 1.01 │ │ AMD EPYC 7351 │ 2.03 │ 2.44 │ 2.35 │ 3 │ 1.20 │ 1.16 │ 1.04 │ │ E5-2660 0 @ 2.20GHz │ 2.13 │ 2.39 │ 2.37 │ 3 │ 1.12 │ 1.11 │ 1.01 │ │ E312xx (Sandy Bridge) │ 1.97 │ 2.2 │ 2.18 │ 3 │ 1.12 │ 1.11 │ 1.01 │ │ E5530 @ 2.40GHz │ 1.65 │ 1.93 │ 1.94 │ 3 │ 1.17 │ 1.18 │ 0.99 │ │ E5645 @ 2.40GHz │ 1.65 │ 1.92 │ 1.94 │ 3 │ 1.16 │ 1.18 │ 0.99 │ │ AMD Opteron 6380 │ 1.47 │ 1.58 │ 1.56 │ 1 │ 1.07 │ 1.06 │ 1.01 │ │ AMD Opteron 6274 │ 1.15 │ 1.35 │ 1.35 │ 1 │ 1.17 │ 1.17 │ 1 │ │ E5440 @ 2.83GHz │ 1.35 │ 1.33 │ 1.42 │ 1 │ 0.99 │ 1.05 │ 0.94 │ │ Cavium ThunderX2 │ 0.84 │ 0.87 │ 0.87 │ 0 │ 1.04 │ 1.04 │ 1 │ └───────────────────────┴──────┴───────┴──────┴──────┴─────────────┴───────────┴────────────────┘
ref, adapt, max — это скорость в гигабайтах в секунду (величина, обратная к среднему арифметическому времени по всем запускам на всех наборах данных). best — номер лучшего алгоритма среди оптимизированных вариантов, от 0 до 3. adapt_boost — относительное преимущество адаптивного алгоритма по сравнению с baseline. max_boost — относительное преимущество лучшего из неадаптивных вариантов по сравнению с baseline. adapt_over_max — относительное преимущество адаптивного алгоритма по сравнению с лучшим неадаптивным.
Как видно, на современных процессорах x86 мы смогли ускорить разжатие на 12–20%. Даже на ARM мы получили плюс 4%, несмотря на то, что мы уделили меньше внимания оптимизации под эту архитектуру. Также заметно, что в среднем по разным наборам данных «бандитский» алгоритм выигрывает у выбранного наперёд лучшего варианта на всех процессорах кроме очень старых Intel.
Выводы
На практике проделанная работа имеет сомнительную полезность. Да, само разжатие LZ4 ускорилось в среднем на 12–20%, а на отдельных наборах данных есть даже более чем двухкратный прирост производительности. Но в целом на время выполнения запроса это влияет существенно меньше. Не так легко найти настоящие запросы, на которых преимущество в скорости будет более пары процентов.
Стоит иметь в виду, что на нескольких кластерах Метрики, предназначенных для выполнения «длинных» запросов, мы решили использовать ZStandard level 1 вместо LZ4: на холодных данных важнее экономить IO и место на дисках.
Наибольшие преимущества от оптимизации разжатия наблюдаются на сильно сжимающихся данных — например, на столбцах с повторяющимися строковыми значениями. Но специально для этого сценария у нас разработано отдельное решение, которое позволяет ускорить такие запросы на порядки.
Ещё одно полезное соображение: оптимизация скорости алгоритма сжатия часто ограничена форматом сжатых данных. LZ4 использует очень хороший формат, но у Lizard, Density и LZSSE другие форматы, которые могут работать быстрее. Возможно, вместо попыток ускорить LZ4 было бы лучше просто подключить LZSSE к ClickHouse.
Внедрение этих оптимизаций в саму библиотеку LZ4 маловероятно: для их использования нужно изменить или дополнить интерфейс библиотеки. На самом деле это очень частый случай при улучшении алгоритмов: оптимизации не укладываются в старые абстракции, требуют их пересмотра. В то же время в оригинальной имплементации уже сейчас исправлено довольно много названий. Например, в части inc- и dec-таблиц теперь всё правильно. Кроме того, несколько недель назад оригинальная имплементация ускорила разжатие на те же 12–15% с помощью копирования по 32 байта, а не по 16, как указано выше. Мы и сами пробовали вариант с 32 байтами — результаты получились не такими классными, но в целом ускорение тоже есть.
Если посмотреть на профиль в начале статьи, можно заметить, что мы могли бы убрать одно лишнее копирование из page cache в userspace (либо с помощью mmap, либо с помощью O_DIRECT и userspace page cache — оба варианта сопряжены с проблемами), а также немного улучшить вычисление чек-сумм (сейчас используется CityHash128 без CRC32-C, а можно взять HighwayHash, FARSH или XXH3). Ускорение этих двух операций полезно для слабо сжимающихся данных, так как они производятся над сжатыми данными.
В любом случае, изменения уже добавлены в master, а полученные в результате этого исследования идеи нашли применение в других задачах. Вот видео с HighLoad++ Siberia, а вот презентация.
