 * от англ. «unscented filtering and nonlinear estimation» (by Переводчик Google)
* от англ. «unscented filtering and nonlinear estimation» (by Переводчик Google)По просьбе dmitriyn решил опубликовать свое видение на так называемый «Unscented Kalman filter», который является распространением линейной фильтрации Калмана на случай, когда уравнения динамики и наблюдения системы нелинейны и не могут быть адекватно линеаризованы.
Как название данного метода фильтрации
UPD: Добавлен комментарий к разделу «ПРИМЕНЕНИЕ UT»
ВВЕДЕНИЕ
В предыдущей статье о линейной фильтрации Калмана описан один из возможных подходов синтеза ФК для случая линеаризованной упрощенной математической модели динамической системы. Описанный там фильтр Калмана в литературе иногда называют «conventional Kalman Filter»[2]. Такое название он получил, т.к. дает наименьшую среднеквадратическую ошибку лишь при соблюдении нескольких гипотез (конвенций) — например, шум является белым и распределен по нормальному закону, матожидание шумов равно нулю, отсутствуют корреляции между шумами и перекрестные связи между фазовыми координатами. Эти ограничения довольно серьезные и на практике часто гипотезы нарушаются. Существуют методики, позволяющие обойти данные ограничения (например, добавление в фазовый вектор фильтра координат для генератора цветного шума и ввода фиктивного возмущения для «смещенного» шума). Все они приводят к увеличению вычислительной сложности (растет размерность задачи) и трудностям синтеза фильтра, устойчивого к нарушению конвенций.
Существует также «Extended Kalman filter» [1], который по структуре своей похож на линейную версию, отличаясь тем, что уравнения динамики и наблюдений содержат нелинейные (степенные, тригонометрические и пр.) функции от фазовых координат (см. уравнения ниже). Это отличие также предполагает наличие перекрестных связей между фазовыми координатами (например, произведение двух координат).
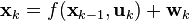

При использовании EKF необходимо на каждом шаге итераций вычислять Якобиан — матрицу частных производных от фазовых координат. Из-за этого сильно возрастает вычислительная сложность и еще острее встает вопрос об устойчивости дискретизированных дифференциальных уравнений. По сути EKF реализует в себе прослойку линеаризации нелинейной динамической системы. В этом заключается главная причина, по которой EKF может оказаться неэффективным. Использование сильно нелинейной модели динамической системы приводит к очень плохой обусловленности задачи, т.е. малая погрешность задания параметров мат. модели будет приводить к большим вычислительным погрешностям. В результате алгоритм утратит робастность (устойчивость к погрешностям).
The unscented Kalman filter (UKF) [3] использует другой подход («unscented transform»). Данный подход
После написания последнего абзаца лично у меня стало вопросов еще больше. Как у Св. Августина, который знал, что такое время, до тех пор пока его не стали о времени спрашивать. Ниже постараюсь разъяснить себе и Вам, уважаемые читатели, суть рассматриваемого метода нелинейной фильтрации.
UNSCENTED TRANSFORM
Пожалуй начну с более подробного описания двух главных проблем линейного фильтра Калмана (ФК) и нелинейного (расширенного, EKF). Первая проблема — конвенции о помехах. Как написано выше, линейный ФК предполагает, что шумы — «белые» и распределены по нормальному закону. Если шумы «цветные», то мы должны синтезировать цифровой формирующий фильтр, при пропускании «белого» шума через который мы получим шум со спектральной характеристикой, эквивалентной (в идеале) или близкой к имеющейся де-факто. Фазовый вектор этого фильтра добавляется в фазовый вектор ФК. Это в свою очередь увеличивает размерность задачи. Допустим, что эта проблема не слишком серьезная. Но есть вторая — проблема нелинейности математической модели. В следствие нелинейности мы должны реализовать некий аппроксиматор, позволяющий линеаризовать нелинейную матричную функцию (см. «h» в уравнении выше) и тем самым предоставить возможность разделить переменные. Переменные необходимо разделить, чтобы была возможность составить уравнения относительно компонентов фазового вектора. В EKF линеаризация производится путем вычисления Якобиана, т.е. для каждого уравнения в «h» вычисляются частные производные по каждой из фазовых переменных. Сама по себе эта операция уже проблема — большой объем вычислений. К тому же для вычисления Якобиана используется разложение в ряд Тэйлора (многомерное) вида:

При этом берется только первый член ряда, а остальные предполагаются пренебрежимо малыми. Таким образом, с использованием такой линеаризации мы получим выражение вида:
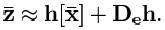
В этом уравнении «De» — оператор вычисления полного дифференциала от матричной функции.
В случае, если нелинейность математической модели мала (модель почти линейна), это утверждение можно считать верным. Однако на практике нелинейности модели таковы, что не допускают отбрасывание членов разложения второго и/или более порядков малости. В таких случаях линеаризация в EKF порождает вычислительную погрешность, пренебречь которой нельзя. В некоторых, частных, случаях удается обойтись без разложения в ряд Тэйлора, но это частные решения, которые жестко привязаны к одному конкретному объекту. Также существует решение, которое урезает ряд Тэйлора до члена второго порядка малости [6]. Оно предполагает вычисление Гессиана — тензора производных второго порядка. Только пожалуйста, не заставляйте меня разжевывать что это такое. Достаточно осознания того факта, что это еще больше утяжеляет EKF и усложняет его реализацию.
Итак, ФК может быть применен к нелинейной модели объекта, если известно некое преобразование, позволяющее спроецировать текущее значение фазового вектора (сделать «нелинейный» прогноз) на следующий шаг итераций. Если такое (адекватное) преобразование неизвестно, то используем EKF с его, часто также неадекватной, линеаризацией и очень большой вычислительной нагрузкой. Таким образом, нужен метод, позволяющий обойтись без линеаризации, используемой в EKF, и не обладающий большей по сравнению с EKF вычислительной сложностью. Таким методом и является «Unscented Transformation» (UT, не путать далее эту аббревиатуру с компьютерной игрой).
Основная идея UT
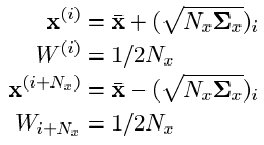
В этих выражениях "Nx" — размерность искомого фазового вектора; "i" — индекс сигма точки (i = 1..Nx); "Wi" — вес i-ой сигма-точки;
 — i-ый столбец матричного квадратного корня от матрицы ковариаций исходного нелинейного преобразования модели домноженной на размерность фазового вектора.
— i-ый столбец матричного квадратного корня от матрицы ковариаций исходного нелинейного преобразования модели домноженной на размерность фазового вектора.Нужно заметить, что это не единственный вариант набора сигма-точек. Приведенные выражения однозначно характеризуют статистику распределения лишь для первого и второго моментов (матожидание и дисперсия). UT, характеризующие статистику распределения искомого вектора до моментов более высоких порядков, отличаются количеством сигма-точек (вообще говоря, количество их не обязательно будет больше чем для выражений выше) и выбором весов. Для простоты изложения подробности опущу. Приведу лишь в качестве примера выражения для UT, учитывающего более высокие порядки моментов статистики распределения фазового вектора:

В принципе про само UT в кратце все. Зачем оно нужно и как используется в UKF написано ниже. Тут осталось оговориться о моментных характеристиках высоких порядков. Что это такое? Интуитивной аналогией могут служить положение, скорость и ускорение движущегося тела. Если считать положение моментом первого порядка, то скорость будет вторым моментом (скорость изменения положения), а ускорение — третьим (скорость изменения скорости). Можно вычислить производную от ускорения — получим четвертый момент. Но есть ли в нем практический смысл? Аналогично с моментными характеристиками в статистике — в большинстве случаев матожидания и дисперсии достаточно. От статистической точности UT, т.е. от способа выбора сигма-точек, эффективность фильтрации зависит, но, наверняка, не на столько сильно, чтобы для большинства практических задач существовала необходимость учитывать моментные характеристики высоких порядков.
ПРИМЕНЕНИЕ UT
Как было сказано выше, UT — это метод, позволяющий избавиться от процедуры линеаризации в нелинейном стохастическом оценивании. Пока мы лишь узнали, что с помощью UT можно подобрать набор точек, достаточно точно характеризующих статистику искомого вектора (фазового вектора). Что нам это дает? Ключевым моментом в фильтрации Калмана является вычисление матрицы кроссковариации (см. матрицу «Кk» в предыдущей статье). Эта матрица в линейном ФК вычисляется как решение матричного уравнения Риккати. В случае нелинейной мат. модели системы эта процедура сильно усложняется. UT позволяет получить матрицу кроссковариации альтернативным путем. Ниже представлена пошаговая процедура фильтрации с использованием метода UT.
- Находим статистические параметры искомого вектора (фазового вектора или вектора наблюдения — вектора выходных сигналов датчиков). Полученные статистические характеристики можно считать постоянными или же обновлять в реальном времени.
- По полученным статистическим данным вычисляем набор сигма точек.
- Пропускаем эти точки через исходную нелинейную мат. модель динамического процесса:

- Вычисляем прогноз матожидания и ковариации:
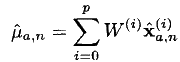

- Пропускаем полученные на третьем шаге точки через модель наблюдения (в общем случае также нелинейную):
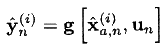
- Вычисляем прогноз наблюдения (в виде взвешенного среднего от значений на предыдущем шаге):

- Вычисляем ковариацию наблюдения:
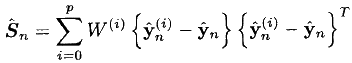
- Находим искомую матрицу кроссковариации:
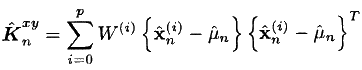
- И наконец пользуемся стандартными выражениями ФК:

Последний блок выражений скопирован из статьи [3] как есть. На мой взгляд что-то в ней не так. Непонятно откуда взяты «yn» без крыжки и матрицы кроссковариации без опознавательных знаков. Но оно и не важно. Про «стандартные выражения ФК» я уже писал. Нужно лишь подставить в них найденный через UT калманов матричный коэффициент усиления (он же матрица кроссковариации) и вычислить скорректированную оценку фазового вектора.
Еще одно замечание по поводу фазового вектора. В выражениях выше есть фазовый вектор с индексом «а» (Хa,n) — это фазовый вектор дополненный (augmented) координатами для шумов процесса и наблюдения. В самом начале я писал, что есть такой прием для обхода ограничения на спектральную характеристику помех. Так вот, в выражениях выше как-то по-тихому сделан переход от дополненных векторов к обычным (там еще и матожидание «мю» есть также простое и дополненное).
ЗАКЛЮЧЕНИЕ
Итак, с помощью UT мы смогли без линеаризации вычислить прогноз фазового вектора и матрицу кроссковариации. Подставив их значения в стандартные выражения для фазы коррекции прогноза ФК (см. «Measurement Update» в статье про линейный ФК) мы получили оценки фазового вектора. Самой ресурсоемкой процедурой при этом является вычисление матричного квадратного корня при формировании набора сигма точек. Общая сложность UKF получается не больше, чем у EKF. Главными преимуществами UKF являются общность синтеза для разных задач (процедура синтеза не зависит от того, с каким объектом вы работаете), а также устойчивость получаемого алгоритма (численная обусловленность UT выше обусловленности процедуры линеаризации в EKF) и отсутствие смещения получаемых оценок (опять же из-за отказа от линеаризации). В качестве иллюстрации приведу графики ошибок оценивания из статьи [3] (см. рис. 1).

Рис. 1. Графики среднеквадратической ошибки и дисперсии оценивания для EKF и UKF
На этом рисунке тонкая линия — среднеквадратическая ошибка для EKF (mean-squarred errors). Точечный график (жирный, в самом низу) — оценка ковариаций (estimated covariances). Два других графика — для UKF. У EKF оценки ковариаций меньше (он сглаживает несколько лучше), но СКО в его оценках очень высокие. У UKF ковариации и СКО находятся примерно на одном уровне. Кстати сказать, мне показалось, что здесь какая-то ошибка. Дисперсия есть квадрат от СКО. Как они могут быть вместе? Тут либо я неправильно трактовал термины (привел их в скобках выше), либо все-таки оценки ковариаций и СКО величины обособленные.
UPD Еще хочу заметить, что сам пока не понял до конца, как этот метод работает, да и правильно ли я понял его суть. Попробую его реализовать — вроде действительно несложный в реализации алгоритм. Посмотрю как он себя покажет, как время будет.
А пока ваши соображения, предложения, замечания… И СПАСИБО ЗА ВНИМАНИЕ!
СПИСОК ЛИТЕРАТУРЫ:
- UKF at Wiki
- A Discussion Related to Orbit Determination Using Nonlinear Sigma Point Kalman Filter
- Julier, S.J.; Uhlmann, J.K. (1997). «A new extension of the Kalman filter to nonlinear systems». Int. Symp. Aerospace/Defense Sensing, Simul. and Controls 3. Retrieved 2008-05-03.
- Fuzzy strong tracking unscented Kalman filter
- Unscented Transform
- M. Athans, R. P. Wishner, and A. Bertolini, “Suboptimal state
estimation for continuous-time nonlinear systems from discrete
noisy measurements,” IEEE Trans. Automat. Contr., vol. AC-13,
pp. 504–518, Oct. 1968.