Как-то раз пришлось реализовывать умножение длинных чисел, через половинки их представления на C++. 128-битные числа были представлены как пара 64-битных. Оказалось что перемножить два 128-битных числа и получить все 256 бит результата по сложности сравнимо с 4-мя произведениями 64-битных половинок. Как же это работает…

Для умножения использовался метод отечественного математика Анатолия Алексеевича Карацубы. Для начала приведу свой комментарий к функции. Он очень много проясняет по алгоритму.
В принципе по комментарию становится понятно как вычисляется результат.
Суть метода можно понять если вывести следующую формулу:
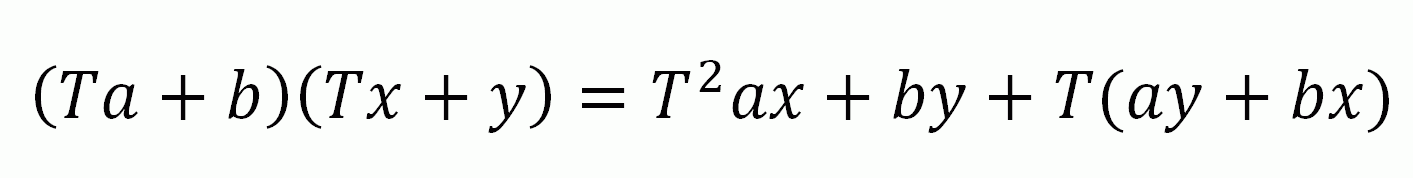
T символизирует отступ, соответственно T^2 — двойной отступ.
Вот код, выполняющий эти операции:
Тип T является типом половинки, типом x0, x1, y0, y1.
Тип N2 является типом половины результата, в 2 раза больше типа T.
Пример использования функции:
Код с результатом выполнения можно посмотреть тут:codepad.org/1OTeGqhA
Код с алгоритмом для разных порядков байтов (LE + BE) тут:codepad.org/f5Pxtiq1
UPDATE1:
Пользователь mark_ablov заметил, что в коде нехватает #undef.
Исправленный код:codepad.org/13U4fuTp
Исправленный полный код (LE + BE):codepad.org/kBazqo8f
UPDATE2:
Пользователь ttim заметил, что приведённый алгоритм, не совсем является методом Карацубы и указал на возможность использования 3-х умножений вместо четырёх.
Формула, вносящая ясность:
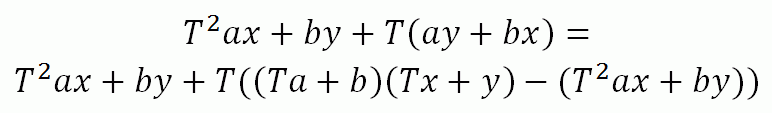
Таким образом, потребуется вычислить лишь 3 произведения:
1. a*x
2. b*y
3. (Ta+b)*(Tx+y)
К сожалению, мне не удастся воспользоваться этой формулой, т.к. я не имею возможности перемножать числа разрядности 128 бит. Собственно моей задачей и являлось реализовать перемножение 128-битных чисел. Дело в том что числа (Ta+b) и (Tx+y) разрядности 128 бит...
UPDATE3:
Пользователь susl продолжил обсуждение алгоритма и показал что вовсе не нужно перемножать 128-битные числа.
Ещё одна формула:
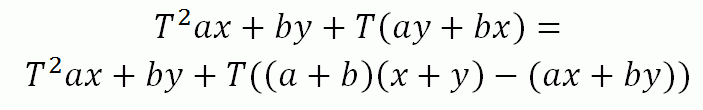
Функцию можно переписать следующим образом:
Исправленный пример: http://codepad.org/w0INBD77
Исправленный пример для LE и BE: http://codepad.org/nB9HqWt1

Для умножения использовался метод отечественного математика Анатолия Алексеевича Карацубы. Для начала приведу свой комментарий к функции. Он очень много проясняет по алгоритму.
//
// Karatsuba multiplication algorithm
//
// +------+------+
// | x1 | x0 |
// +------+------+
// *
// +------+------+
// | y1 | y0 |
// +------+------+
// =
// +-------------+-------------+
// + | x1*y1 | x0*y0 |
// +----+-+------+------+------+
// . . .
// . . .
// +-+------+------+
// + | x0*y1 + x1*y0 |
// +-+------+------+
//
В принципе по комментарию становится понятно как вычисляется результат.
Суть метода можно понять если вывести следующую формулу:

T символизирует отступ, соответственно T^2 — двойной отступ.
Вот код, выполняющий эти операции:
//
// Params:
// T - is type of x0, x1, y0 and y1 halves
// T2 - is type of x, y and half of res
//
template<typename T, typename T2>
inline void Karatsuba_multiply(T * const x, T * const y, T2 * res)
{
// Define vars (depending from byte order)
#define ptrRes ((T*)res)
T2 & lowWord = (T2&)(ptrRes[0]);
T2 & midWord = (T2&)(ptrRes[1]);
T2 & highWord = (T2&)(ptrRes[2]);
T & highByte = (T &)(ptrRes[3]);
#undef ptrRes
const T & x0 = x[0];
const T & x1 = x[1];
const T & y0 = y[0];
const T & y1 = y[1];
// Multiply action
lowWord = x0 * y0;
highWord = x1 * y1;
T2 m1 = x0 * y1;
T2 m2 = x1 * y0;
midWord += m1;
if (midWord < m1) highByte++;
midWord += m2;
if (midWord < m2) highByte++;
}
Тип T является типом половинки, типом x0, x1, y0, y1.
Тип N2 является типом половины результата, в 2 раза больше типа T.
Пример использования функции:
int main()
{
typedef unsigned char u8;
typedef unsigned short u16;
typedef unsigned int u32;
u16 a = 1000;
u16 b = 2000;
u32 r = 0;
u8 * a_ptr = (u8*)&a;
u8 * b_ptr = (u8*)&b;
u16 * r_ptr = (u16*)(void*)&r;
Karatsuba_multiply(a_ptr, b_ptr, r_ptr);
cout << r;
}
Код с результатом выполнения можно посмотреть тут:
Код с алгоритмом для разных порядков байтов (LE + BE) тут:
UPDATE1:
Пользователь mark_ablov заметил, что в коде нехватает #undef.
Исправленный код:
Исправленный полный код (LE + BE):
UPDATE2:
Пользователь ttim заметил, что приведённый алгоритм, не совсем является методом Карацубы и указал на возможность использования 3-х умножений вместо четырёх.
Формула, вносящая ясность:

Таким образом, потребуется вычислить лишь 3 произведения:
1. a*x
2. b*y
3. (Ta+b)*(Tx+y)
К сожалению, мне не удастся воспользоваться этой формулой, т.к. я не имею возможности перемножать числа разрядности 128 бит. Собственно моей задачей и являлось реализовать перемножение 128-битных чисел. Дело в том что числа (Ta+b) и (Tx+y) разрядности 128 бит...
UPDATE3:
Пользователь susl продолжил обсуждение алгоритма и показал что вовсе не нужно перемножать 128-битные числа.
Ещё одна формула:

Функцию можно переписать следующим образом:
//
// Params:
// T - is type of x0, x1, y0 and y1 halves
// T2 - is type of x, y and half of res
//
template<typename T, typename T2>
inline void Karatsuba_multiply(T * const x, T * const y, T2 * res)
{
// Define vars (depending from byte order)
#define ptrRes ((T*)res)
T2 & lowWord = (T2&)(ptrRes[0]);
T2 & midWord = (T2&)(ptrRes[1]);
T2 & highWord = (T2&)(ptrRes[2]);
T & highByte = (T &)(ptrRes[3]);
#undef ptrRes
const T & x0 = x[0];
const T & x1 = x[1];
const T & y0 = y[0];
const T & y1 = y[1];
// Multiply action
lowWord = x0 * y0;
highWord = x1 * y1;
//T2 m1 = x0 * y1;
//T2 m2 = x1 * y0;
T2 m = (x0+x1)*(y0+y1) - (lowWord + highWord);
//midWord += m1;
//if (midWord < m1) highByte++;
//midWord += m2;
//if (midWord < m2) highByte++;
midWord += m;
if (midWord < m) highByte++;
}
Исправленный пример: http://codepad.org/w0INBD77
Исправленный пример для LE и BE: http://codepad.org/nB9HqWt1