Сейчас существует множество алгоритмов сжатия информации. Большинство из них широко известны, но есть и некоторые весьма эффективные, но, тем не менее, малоизвестные алгоритмы. Эта статья рассказывает о методе арифметического кодирования, который является лучшим из энтропийных, но тем не менее мало кто о нём знает.
Прежде чем рассказывать об арифметическом кодировании, надо сказать пару слов об алгоритме Хаффмана. Этот метод эффективен, когда частоты появления символов пропорциональны 1/2n (где n – натуральное положительное число). Это утверждение становится очевидным, если вспомнить, что коды Хаффмана для каждого символа всегда состоят из целого числа бит. Рассмотрим ситуацию, когда частота появление символа равна 0,2, тогда оптимальный код для кодирования это символа должен иметь длину –log2(0,2)=2,3 бита. Понятно, что префиксный код Хаффмана не может иметь такую длину, т.е. в конечном итоге это приводит к ухудшению сжатия данных.
Арифметическое кодирование предназначено для того, чтобы решить эту проблему. Основная идея заключается в том, чтобы присваивать коды не отдельным символам, а их последовательностям.
Вначале рассмотрим идею, лежащую в основе алгоритма, затем рассмотрим небольшой практический пример.
Как и во всех энтропийных алгоритмах мы обладаем информацией о частоте использования каждого символа алфавита. Эта информация является исходной для рассматриваемого метода. Теперь введём понятие рабочего отрезка. Рабочим называется полуинтервал [a;b) с расположенными на нём точками. Причём точки расположены т.о., что длины образованных ими отрезков равны частоте использования символов. При инициализации алгоритма a=0 b=1.
Один шаг кодирования заключается в простой операции: берётся кодируемый символ, для него ищется соответствующий участок на рабочем отрезке. Найденный участок становится новым рабочим отрезком (т.е. его тоже необходимо разбить с помощью точек).
Эта операция выполняется для некоторого количества символов исходного потока. Результатом кодирования цепочки символов является любое число (а также длина его битовой записи) с итогового рабочего отрезка (чаще всего берётся левая граница отрезка).
Звучит это довольно сложно. Давайте попробуем разобраться с помощью небольшого примера. Закодируем сообщение «ЭТОТ_МЕТОД_ЛУЧШЕ_ХАФФМАНА» с помощью описанного метода.
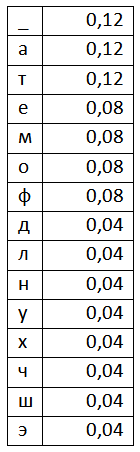
Составив таблицу частоты появления символов, мы можем приступать к кодированию. На первом этапе составим рабочий отрезок. Выглядеть он будет так:

Берём первый символ из потока, это символ «Э». Соответствующий ему отрезок – отрезок [0,96;1). Если бы мы хотели закодировать один символ, то результатом кодирования было бы любое число из этого отрезка. Но мы не остановимся на одном символе, а добавим ещё один. Символ «Т». Для этого составим новый рабочий отрезок с a=0,96 и b=1. Разбиваем этот отрезок точками точно так же как мы сделали это для исходного отрезка и считываем новый символ «Т». Символу «Т» соответствует диапазон [0,24;0,36), но наш рабочий отрезок уже сократился до отрезка [0,96;1). Т.е. границы нам необходимо пересчитать. Сделать это можно с помощью двух следующих формул: High=Lowold+(Highold-Lowold)*RangeHigh(x), Low=Lowold+(Highold-Lowold)*RangeLow(x), где Lowold – нижняя граница интервала, Highold – верхняя граница интервала RangeHigh и RangeLow – верхняя и нижняя границы кодируемого символа.
Пользуясь этими формулами, закодируем первое слово сообщения целиком:
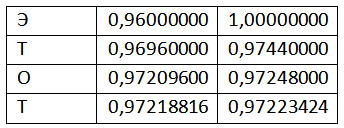
Результатом кодирования будет любое число из полуинтервала [0,97218816; 0,97223424).
Предположим, что результатом кодирования была выбрана левая граница полуинтервала, т.е. число 0,97218816.
Рассмотрим процесс декодирования. Код лежит в полуинтервале [0,96;1). Т.е. первый символ сообщения «Э». Чтобы декодировать второй символ (который кодировался в полуинтервале [0,96;1)) полуинтервал нужно нормализовать, т.е. привести к виду [0;1). Это делается с помощью следующей формулы: code=(code-RangeLow(x))/(RangeHigh(x)-RangeLow(x)), где code – текущее значение кода.
Применяя эту формулу, получаем новое значение code=(0,97218816-0,96)/(1-0,96)= 0,304704. Т.е. второй символ последовательности «Т».
Снова применим формулу: code=(0,304704-0,24)/(0,36-0,24)= 0,5392. Третий символ последовательности – «О».
Продолжая декодирование, по описанной схеме мы можем полностью восстановить исходный текст.
Т.о. мы с вами рассмотрели алгоритм кодирования и декодирования с помощью самого эффективного из всех энтропийных алгоритмов. Надеюсь, из этой статьи вы узнали что-то новое и поняли основные идеи, лежащие в алгоритме арифметического кодирования.
Прежде чем рассказывать об арифметическом кодировании, надо сказать пару слов об алгоритме Хаффмана. Этот метод эффективен, когда частоты появления символов пропорциональны 1/2n (где n – натуральное положительное число). Это утверждение становится очевидным, если вспомнить, что коды Хаффмана для каждого символа всегда состоят из целого числа бит. Рассмотрим ситуацию, когда частота появление символа равна 0,2, тогда оптимальный код для кодирования это символа должен иметь длину –log2(0,2)=2,3 бита. Понятно, что префиксный код Хаффмана не может иметь такую длину, т.е. в конечном итоге это приводит к ухудшению сжатия данных.
Арифметическое кодирование предназначено для того, чтобы решить эту проблему. Основная идея заключается в том, чтобы присваивать коды не отдельным символам, а их последовательностям.
Вначале рассмотрим идею, лежащую в основе алгоритма, затем рассмотрим небольшой практический пример.
Как и во всех энтропийных алгоритмах мы обладаем информацией о частоте использования каждого символа алфавита. Эта информация является исходной для рассматриваемого метода. Теперь введём понятие рабочего отрезка. Рабочим называется полуинтервал [a;b) с расположенными на нём точками. Причём точки расположены т.о., что длины образованных ими отрезков равны частоте использования символов. При инициализации алгоритма a=0 b=1.
Один шаг кодирования заключается в простой операции: берётся кодируемый символ, для него ищется соответствующий участок на рабочем отрезке. Найденный участок становится новым рабочим отрезком (т.е. его тоже необходимо разбить с помощью точек).
Эта операция выполняется для некоторого количества символов исходного потока. Результатом кодирования цепочки символов является любое число (а также длина его битовой записи) с итогового рабочего отрезка (чаще всего берётся левая граница отрезка).
Звучит это довольно сложно. Давайте попробуем разобраться с помощью небольшого примера. Закодируем сообщение «ЭТОТ_МЕТОД_ЛУЧШЕ_ХАФФМАНА» с помощью описанного метода.

Составив таблицу частоты появления символов, мы можем приступать к кодированию. На первом этапе составим рабочий отрезок. Выглядеть он будет так:

Берём первый символ из потока, это символ «Э». Соответствующий ему отрезок – отрезок [0,96;1). Если бы мы хотели закодировать один символ, то результатом кодирования было бы любое число из этого отрезка. Но мы не остановимся на одном символе, а добавим ещё один. Символ «Т». Для этого составим новый рабочий отрезок с a=0,96 и b=1. Разбиваем этот отрезок точками точно так же как мы сделали это для исходного отрезка и считываем новый символ «Т». Символу «Т» соответствует диапазон [0,24;0,36), но наш рабочий отрезок уже сократился до отрезка [0,96;1). Т.е. границы нам необходимо пересчитать. Сделать это можно с помощью двух следующих формул: High=Lowold+(Highold-Lowold)*RangeHigh(x), Low=Lowold+(Highold-Lowold)*RangeLow(x), где Lowold – нижняя граница интервала, Highold – верхняя граница интервала RangeHigh и RangeLow – верхняя и нижняя границы кодируемого символа.
Пользуясь этими формулами, закодируем первое слово сообщения целиком:

Результатом кодирования будет любое число из полуинтервала [0,97218816; 0,97223424).
Предположим, что результатом кодирования была выбрана левая граница полуинтервала, т.е. число 0,97218816.
Рассмотрим процесс декодирования. Код лежит в полуинтервале [0,96;1). Т.е. первый символ сообщения «Э». Чтобы декодировать второй символ (который кодировался в полуинтервале [0,96;1)) полуинтервал нужно нормализовать, т.е. привести к виду [0;1). Это делается с помощью следующей формулы: code=(code-RangeLow(x))/(RangeHigh(x)-RangeLow(x)), где code – текущее значение кода.
Применяя эту формулу, получаем новое значение code=(0,97218816-0,96)/(1-0,96)= 0,304704. Т.е. второй символ последовательности «Т».
Снова применим формулу: code=(0,304704-0,24)/(0,36-0,24)= 0,5392. Третий символ последовательности – «О».
Продолжая декодирование, по описанной схеме мы можем полностью восстановить исходный текст.
Т.о. мы с вами рассмотрели алгоритм кодирования и декодирования с помощью самого эффективного из всех энтропийных алгоритмов. Надеюсь, из этой статьи вы узнали что-то новое и поняли основные идеи, лежащие в алгоритме арифметического кодирования.