
Вступление
Одна из самых главных проблем при работе с данными — это их размер. Нам всегда хочется, что бы уместилось как можно больше. Но иногда этого не сделать. Поэтому нам на помощь приходят различные архиваторы. Но как они сжимают данные? Я не буду писать о принципе их работы, лишь расскажу о нескольких алгоритмах сжатия, которые они используют.
Алгоритм Хаффмана
Коды или Алгоритм Хаффмана (Huffman codes) — широко распространенный и очень эффективный метод сжатия данных, который, в зависимости от характеристик этих данных, обычно позволяет сэкономить от 20% до 90% объема.
Рассматриваются данные, представляющие собой последовательность символов. В жадном алгоритме Хаффмана используется таблица, содержащая частоты появления тех или иных символов. С помощью этой таблицы определяется оптимальное представление каждого символа в виде бинарной строки.
Построение кода
В основу алгоритма Хаффмана положена идея: кодировать более коротко те символы, которые встречаются чаще, а те, которые встречаются реже кодировать длиннее. Для построения кода Хаффмана нам необходима таблица частот символов. Рассмотрим пример построения кода на простой строке abacaba
- a b c
- 4 2 1
Обрабатываем b и c
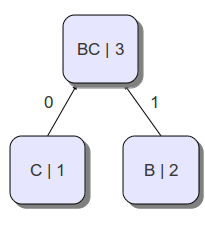
Следующим шагом будет построение дерева, где вершины — «символы», а пути до них соответствуют их префиксным кодам. Для этого на каждом шаге будем брать два символа с минимальной частотой вхождения, и объединять их в новые так называемые символы с частотой равной сумме частот тех, которые мы объединяли, а также соединять их рёбрами, образуя таким образом дерево(см. рисунок). Выбирать минимальные два символа будем из всех символов, исключая те, которые мы уже выбирали. В примере мы объединим символы b и с в символ bc с частотой 3. Далее объединим a и bc в символ abc, получив тем самым дерево. Теперь пути от корня (abc) до листьев и есть Коды Хаффмана(каждому ребру соответствует либо 1 либо 0)
- a b c
- 0 11 10
Получившееся дерево
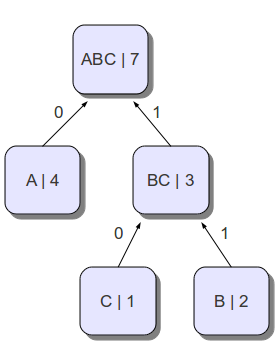
Преобразование MTF
Преобразование MTF (move-to-front, движение к началу) — алгоритм кодирования, используемый для предварительной обработки данных (обычно потока байтов) перед сжатием, разработанный для улучшения производительности последующего кодирования.
Построение кода
Изначально каждое возможное значение байта записывается в список (алфавит), в ячейку с номером, равным значению байта, т.е. (0, 1, 2, 3, …, 255). В процессе обработки данных этот список изменяется. По мере поступления очередного символа на выход подается номер элемента, содержащего его значение. После чего этот символ перемещается в начало списка, смещая остальные элементы вправо.
Современные алгоритмы (например, bzip2) перед алгоритмом MTF используют алгоритм BWT, поэтому в качестве примера рассмотрим строку s=«BCABAAA», полученную из строки «ABACABA» в результате преобразования Барроуза-Уиллера (о нем далее). Первый символ строки s='B' является вторым элементом алфавита «ABC», поэтому на вывод подаётся 1. После перемещения 'B' в начало алфавита тот принимает вид «BAC». Дальнейшая работа алгоритма:
- Символ Список Вывод
- B ABC 1
- C BAC 2
- A CBA 2
- B ACB 2
- A BAC 1
- A ABC 0
- A ABC 0
Таким образом, результат работы алгоритма MTF(s):«1222100».
Обратное преобразование
Пусть даны строка s= «1222100» и исходный алфавит «ABC». Символ с номером 1 в алфавите — это 'B'. На вывод подаётся 'B', и этот символ перемещается в начало алфавита. Символ с номером 2 в алфавите — это 'A', поэтому 'A' подается на вывод и перемещается в начало алфавита. Дальнейшее преобразование происходит аналогично.
- Символ Список Вывод
- 1 ABC B
- 2 BAC C
- 2 CBA A
- 2 ACB B
- 1 BAC A
- 0 ABC A
- 0 ABC A
Значит, исходная строка s = «BCABAAA».
Преобразование Барроуза-Уиллера
Преобразование Барроуза — Уилера (Burrows-Wheeler transform, BWT) — это алгоритм, используемый в техниках сжатия данных для преобразования исходных данных.
Bzip2 использует преобразование Барроуза-Уилера для превращения последовательностей многократно чередующихся символов в строки одинаковых символов, затем применяет преобразование MTF, и в конце кодирование Хаффмана.
Работа алгоритма
Преобразование выполняется в три этапа. На первом этапе составляется таблица всех циклических сдвигов входной строки. На втором этапе производится лексикографическая (в алфавитном порядке) сортировка строк таблицы. На третьем этапе в качестве выходной строки выбирается последний столбец таблицы преобразования. Следующий пример иллюстрирует описанный алгоритм:
Пусть нам дана исходная строка s=«ABACABA».
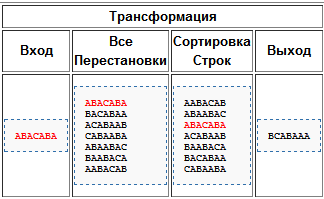
Результат вкратце запишем так: BWT(s)=(«BCABAAA», 3), где 3 — это номер исходной строки в отсортированной матрице, так как он может понадобиться для обратного преобразования.
Следует заметить, что иногда в исходной строке приводится так называемый символ конца строки $, который в преобразовании будет считаться последним символом, тогда сохранение номера исходной строки не требуется. При аналогичном вышеприведённом преобразовании та строчка в матрице, которая будет заканчиваться на символ конца строки и будет исходной («ABACABA$»). При этом при сортировке матрицы данный символ будет рассматриваться как самый последний после всех символов алфавита. Тогда результат можно записать так BWT(s)="$CBBAAAA". Он будет эквивалентен первому, так как также содержит все символы исходной строки.
Обратное преобразование
Пусть нам дано: BWT(s)=(«BCABAAA», 3). Тогда выпишем в столбик нашу преобразованную последовательность символов «BCABAAA». Запишем её как последний столбик предыдущей матрицы (при прямом преобразовании Барроуза — Уилера), при этом все предыдущие столбцы оставляем пустыми. Далее построчно отсортируем матрицу, затем в предыдущий столбец запишем «BCABAAA». Опять построчно отсортируем матрицу. Продолжая таким образом, можно восстановить полный список всех циклических перестановок строки, которую нам надо найти. Выстроив полный отсортированный список перестановок, выберем строку с номером, который нам был изначально дан. В итоге мы получим искомую строку. Алгоритм обратного преобразования описан в таблице ниже:
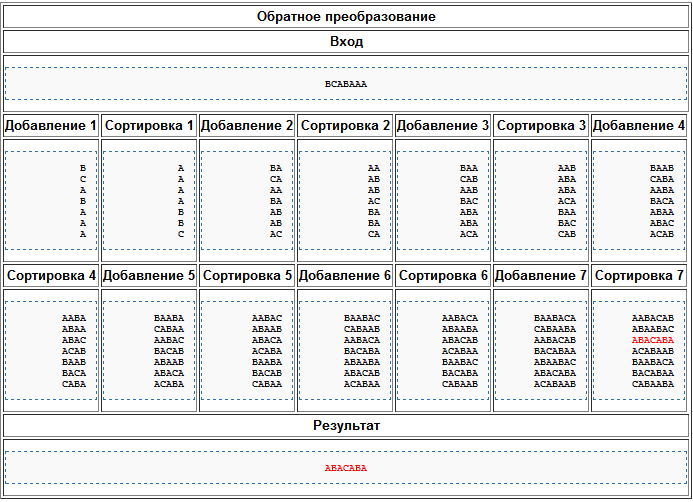
Следует также заметить, что если нам было бы дано BWT(s)="$CBBAAAA", то мы также получили бы нашу исходную строку, только с символом конца строки $ на конце: ABACABA$.
Заключение
Эти три алгоритма используются в наше время в утилите bzip2 для сжатия данных. Но и не только, поскольку данные алгоритмы являются очень эффективными в своей работе.