Однажды в студеную зимнюю пору я столкнулся с упоминанием того, что кто-то в Facebook пытается подтвердить теорию шести рукопожатий. Для тех кто не в курсе, эта теория заключается в том, что все жители земли в среднем знакомы друг с другом через цепочку из пяти друзей (т.е. шести рукопожатий). Подробнее об истории этой теории можно прочитать в википедии, там же можно узнать о том, что Майкрософт несколько лет назад пыталась подтвердить эту теорию на основе данных о контакт-листах мессенджера MSN — в результате у них получилось 6,6 рукопожатий, что вполне вписывается в теорию.
Очень мне захотелось эту теорию подтвердить самому, используя данные, которые есть под рукой — ВКонтакте. Для претворения моей странной идеи в жизнь надо было решить целый комплекс проблем:
С засильем социальных сетей в современной жизни вопрос о том, где взять данные о социальных связях, не такой уж сложный. Конечно, было бы прекрасно взять данные о друзьях из Facebook, ведь он охватывает весь мир, да и народа там много. Но через публичный API вытянуть список друзей для любого человека я не могу, а парсить страничку — не самый эффективный вариант, ибо Facebook список друзей выплевывает в виде dhtml, примерно по 1кб данных на одного друга, итого 400М человек * 130 друзей в среднем * 1кб = 52 Тб трафика. Такой объем трафика малость не вписывался в стремившийся к нулю бюджет исследования, и вариант с Facebook был откинут.
Мой взгляд был устремлен на ВКонтакте. Да, он охватывает только Россию и СНГ (причем неравномерно — в одноклассниках, к примеру, публика постарше). Да, там огромное количество ботов. ВКонтакте неидеален, но зато умеет раздавать список друзей в json-формате через запрос к al_friends.php.
Но как эти данные хранить и обрабатывать?
Спустя трое суток и полтора терабайта трафика база друзей была получена (между прочим, всего лишь 22Гб). И тут возникает самый интересный вопрос: как же считать дистанцию между пользователями?
При решении ресурсоемких задач я люблю делать такие их реализации, которые будут нормально работать даже на моем скромном нетбуке, а потом уже включать тяжелую артиллерию. В качестве тяжелой артиллерии использовался скромный сервер с двумя шестиядерными ксеонами X5650 и 32Гб памяти. На нем дистанция считалась уже за 10 секунд на поток. С учетом распараллеливания, за минуту рассчитывались дистанции между 144 парами пользователей.
Далее начались странности с данными. Почти 50% всех пользователей с ненулевым количеством друзей входило в абсолютно независимые кластеры, в которых нет внешних связей (или таких связей полторы штуки на весь кластер). Грубо говоря, 50 человек зафрендили друг друга и больше никого. Довольно странное поведение, не так ли? Да, возможно, это сектанты и им религия запрещает френдить ВКонтакте не-членов секты. Но врядли, скорее всего это боты.
Выкинув ботов, отловленных подобным неожиданными способом, было проанализировано 6773 пары пользователей и получился очень интересный результат:
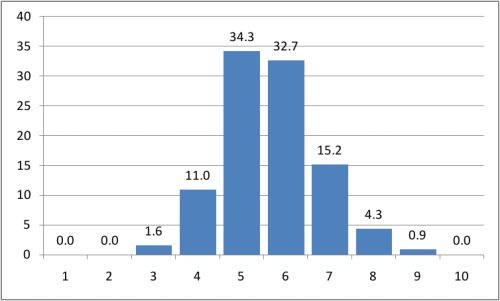
На гистограмме по оси x — длина найденной кратчайшей цепочки друзей, а по оси y — вероятность ее найти в процентах.
Таком образом, в среднем, между двумя случайными пользователями ВКонтакте есть 5.65 друзей (т.е. 6.65 рукопожатий). Эта цифра вполне вписывается в изначально проверяемую теорию, к тому же довольно точно совпадает с результатом, полученным в Microsoft (у них вышло 6.6). Так что полученный результат можно считать еще одним подтверждением теории шести рукопожатий.
Очень мне захотелось эту теорию подтвердить самому, используя данные, которые есть под рукой — ВКонтакте. Для претворения моей странной идеи в жизнь надо было решить целый комплекс проблем:
- На каких данных это все расчитывать.
- Где эти данные взять.
- Как эти данные сохранять.
- Каким алгоритмом воспользоваться для расчетов.
С засильем социальных сетей в современной жизни вопрос о том, где взять данные о социальных связях, не такой уж сложный. Конечно, было бы прекрасно взять данные о друзьях из Facebook, ведь он охватывает весь мир, да и народа там много. Но через публичный API вытянуть список друзей для любого человека я не могу, а парсить страничку — не самый эффективный вариант, ибо Facebook список друзей выплевывает в виде dhtml, примерно по 1кб данных на одного друга, итого 400М человек * 130 друзей в среднем * 1кб = 52 Тб трафика. Такой объем трафика малость не вписывался в стремившийся к нулю бюджет исследования, и вариант с Facebook был откинут.
Мой взгляд был устремлен на ВКонтакте. Да, он охватывает только Россию и СНГ (причем неравномерно — в одноклассниках, к примеру, публика постарше). Да, там огромное количество ботов. ВКонтакте неидеален, но зато умеет раздавать список друзей в json-формате через запрос к al_friends.php.
Но как эти данные хранить и обрабатывать?
- Можно пойти в лоб и писать сразу в MySQL: паук выплевывает 100 пользователей в секунду, у каждого 130 друзей, итого 13000 вставок в БД в секунду. Цифра не запредельная, но с учетом того, что паук работал на слабом сервере (старый одноядерный атлон), не совсем радужная.
- Можно писать текстовый дамп на диск, а потом всасывать его в базу данных. При таком раскладе база будет весить примерно (4 байта (размер поля user_id) + 4 байта (размер поля friend_id) + 8 байтов на оверхед и индексы) * 80М пользователей вконтакте * 130 друзей = 166Гб. Многовато будет. Причем выборка с такой базы всех друзей пользователя не будет выглядеть как суперэффективный запрос.
- Можно забить на MySQL и использовать какое-нибудь hash-value хранилище. В него писать пару «user_id array(friend_id friend_id ...)», таким макаром база сдуется раза в четыре и всех друзей будет выбирать одним обращением к диску. В качестве хранилища изначально был выбран Kyoto Cabinet, но из-за каких-то странных аномалий в производительности на большой базе состоялся переезд на гугловый LevelDB.
Спустя трое суток и полтора терабайта трафика база друзей была получена (между прочим, всего лишь 22Гб). И тут возникает самый интересный вопрос: как же считать дистанцию между пользователями?
- Алгоритм Флойда-Уоршелла, позволил бы рассчитать дистанции от всех пользователей ко всем. Чудесный алгоритм, но у него есть неприятное требование памяти — необходимо хранить квадратную матрицу user_id/user_id, которая бы занимала 1 байт * 80М пользователей * 80М пользователей = 6400 Тб. Совсем многовато.
- Алгоритм Дейкстры, позволил бы найти дистанции от одного пользователя до всех остальных сразу. Существует довольно много эффективных его реализаций, одна из которых и была ради эксперимента использована. Алгоритм чудесно работал на 1% синтетическом сэмпле всей базы, но при запуске уже на среднем 10% семпле базы начинал жестоко тормозить в довольно неожиданном месте — обход большого дерева друзей постоянно лазил в случайные места памяти и ловил почти 100% CACHE_MISS и без того слабого процессора. Говоря человеческим языком, данные не помещались в кэш процессора, и тут начинались феерические тормоза.
- Двунаправленный поиск. Да, не самый элегантный в мире алгоритм, зато простой как таблица умножения. Позволяет найти кратчайшую дистанцию между двумя пользователями. Реализация его писалась с использованием битовых полей, которые элегантно упихивались в кэш процессора, в результате дистанцию между двумя людьми алгоритм находил где-то за полминуты.
При решении ресурсоемких задач я люблю делать такие их реализации, которые будут нормально работать даже на моем скромном нетбуке, а потом уже включать тяжелую артиллерию. В качестве тяжелой артиллерии использовался скромный сервер с двумя шестиядерными ксеонами X5650 и 32Гб памяти. На нем дистанция считалась уже за 10 секунд на поток. С учетом распараллеливания, за минуту рассчитывались дистанции между 144 парами пользователей.
Далее начались странности с данными. Почти 50% всех пользователей с ненулевым количеством друзей входило в абсолютно независимые кластеры, в которых нет внешних связей (или таких связей полторы штуки на весь кластер). Грубо говоря, 50 человек зафрендили друг друга и больше никого. Довольно странное поведение, не так ли? Да, возможно, это сектанты и им религия запрещает френдить ВКонтакте не-членов секты. Но врядли, скорее всего это боты.
Выкинув ботов, отловленных подобным неожиданными способом, было проанализировано 6773 пары пользователей и получился очень интересный результат:

На гистограмме по оси x — длина найденной кратчайшей цепочки друзей, а по оси y — вероятность ее найти в процентах.
Таком образом, в среднем, между двумя случайными пользователями ВКонтакте есть 5.65 друзей (т.е. 6.65 рукопожатий). Эта цифра вполне вписывается в изначально проверяемую теорию, к тому же довольно точно совпадает с результатом, полученным в Microsoft (у них вышло 6.6). Так что полученный результат можно считать еще одним подтверждением теории шести рукопожатий.