За счет чего же мы наблюдаем постоянный рост производительности однопоточных программ? В данный момент мы находимся на той ступени развития микропроцессорных технологий, когда прирост скорости работы однопоточных приложений зависит только от памяти. Количество ядер растет, но частота зафиксировалась в пределах 4 ГГц и не дает прироста производительности.
Скорость и частота работы памяти — это то основное за счет чего мы получаем «свой кусок бесплатного торта» (ссылка). Именно поэтому важно использовать память, настолько эффективно, насколько мы можем это делать, а тем более такую быструю как кэш. Для оптимизации программы под конкретный компьютер, полезно знать характеристики кэш-памяти процессора: количество уровней, размер, длину строки. Особенно это важно в высокопроизводительном коде — ядра систем, математические библиотеки.
Как же определить характеристики кэша автоматический? (естественно cpuinfo распарсить не считается, хотя-бы потому-что в конечном итоге мы бы хотели получить алгоритм, который можно без труда реализовать в других ОС. Удобно, не правда ли? ) Именно этим мы сейчас и займемся.
В данный момент существуют и широко используются три разновидности кэш-памяти: кэш с прямым отображением, ассоциативный кэш и множественно-ассоциативный кэш.

LRU — вытеснение самой «долго не использованной» строки, кэш памяти.
Чтобы определить количество уровней кэша нужно рассмотреть порядок обращений к памяти, на котором будет четко виден переход. Разные уровни кэша отличаются прежде всего скоростью отклика памяти. В случае «кэш-промаха» для кэша L1 будет произведен поиск данных в следующих уровнях памяти, при этом если размер данных больше L1 и меньше L2 — то скоростью отклика памяти будет скорость отклика L2. Предыдущее утверждение так же верно в общем случаи.
Ясно что нужно подобрать тест на котором, мы будем четко видеть кэш промахи и протестировать его на различных размерах данных.
Зная логику множественно-ассоциативных кэшей, работающих по алгоритму LRU не трудно придумать алгоритм на котором кэш «валится», ничего хитрого — проход по строке. Критерием эффективности будем считать время одного обращения к памяти. Естественно нужно последовательно обращаться ко всем элементам строки, повторяя многократно для усреднения результата. К примеру возможны случаи, когда строка умещается в кэше но для первого прохода мы грузим строку из оперативной памяти и потому получаем совсем неадекватное время.
Хочется увидеть что-то подобное ступенькам, проходя по строкам разной длины. Для определения характера ступенек рассмотрим пример прохода по строке для прямого и ассоциативного кэша, случай с множественно-ассоциативным кэшем будет среднем между кэшем с прямым отображением и ассоциативным кэшем.
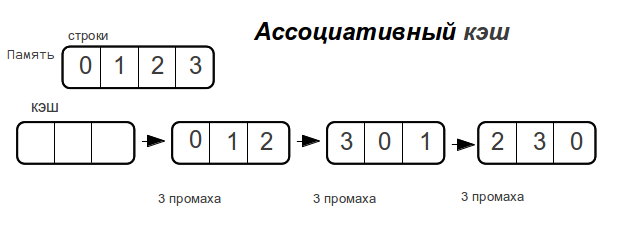
Ассоциативный кэш
Как только размер данных превышает размер кэш-памяти,
полностью ассоциативный кэш «промахивается» при каждом обращении к памяти.
Прямой кэш
Рассмотрим разные размеры строк. — показывает максимальное количество промахов, которое потратит процессор для доступа к элементам массива при следующем проходе по строке.




Как видно время доступа к памяти возрастает не резко, а по мере увеличения объема данных. Как только размер данных превысит размер кэша, то промахи будут при каждом обращении к памяти.
Потому у ассоциативного кэша ступенька будет вертикальной, а у прямого — плавно возрастать вплоть до двойного размера кэша. Множественно ассоциативный кэш будет средним случаем, «бугорком», хотя бы потому, что время-доступа не может быть лучше прямого.
Если-же говорить о памяти — то самая быстрая это кэш, следом идет оперативная, самая медленная это swap, про него мы в дальнейшем говорить не будем. В свою очередь у разных уровней кэша (как правило сегодня процессоры имеют 2-3 уровня кэша) разная скорость отклика памяти: чем больше уровень, тем меньше скорость отклика. И поэтому, если строка помещается в первый уровень кэша, (который кстати полностью ассоциативный) время отклика будет меньше, чем у строки значительно превышающей размеры кэша первого уровня. По-этому на графике времени отклика памяти от размеров строки будет несколько плато — плато* отклика памяти, и плато вызванные различными уровнями кэша.
*Плато функции — { i:x, f(xi) — f(xi+1) < eps: eps → 0 }
Для реализации будем использовать Си (ANSI C99).
Быстро написан код, обычный проход по строкам разной длины, меньше 10мб, выполняющийся многократно. (Будем приводить небольшие куски программы, несущие смысловую нагрузку).
Смотрим на график — и видим одну большую ступеньку. Но ведь в теории получается все, просто замечательно. Стало быть нужно понять: из за чего это происходит? И как это исправить?
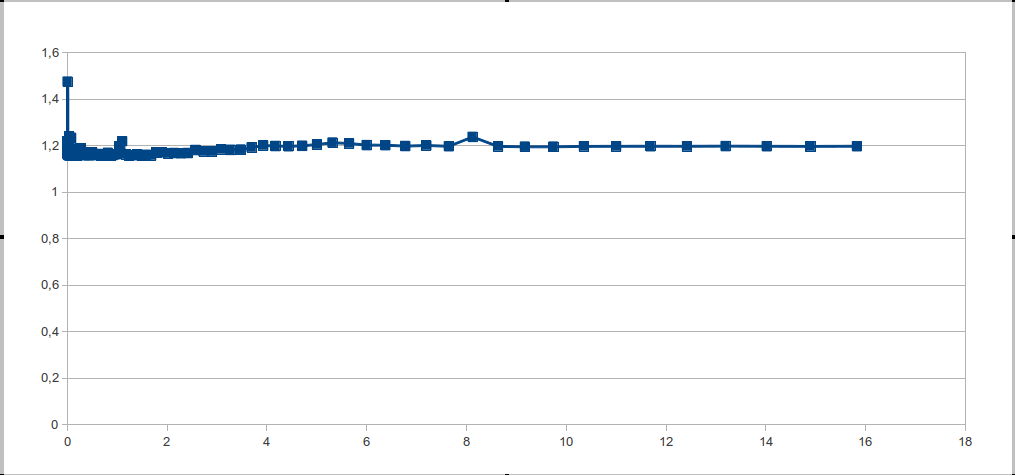
Очевидно что это может происходить по двум причинам: либо в процессоре нет кэш памяти, либо процессор так хорошо угадывает обращения к памяти. Поскольку первый вариант ближе к фантастике причина всему хорошее предсказание обращений.
Дело в том, что сегодня далеко не топовые процессоры, помимо принципа пространственной локальности, предсказывают также и арифметическую прогрессию в порядке обращения к памяти. Поэтому нужно рандомизовать обращения к памяти.
Длина рандомизованного массива должна быть сопоставимой с длиной основной строки, чтобы избавиться от большой гранулярности обращений, так же длина массива не должна быть степенью двойки, из-за этого происходили «наложения» — следствием чего могут — быть выбросы. Лучше всего задать гранулярность константно, в том числе, если гранулярность простое число, то можно избежать эффектов наложений. А длина рандомиованого массива — функция от длинны строки.
После чего мы удивили столь долгожданную «картинку», о которой говорили в начале.
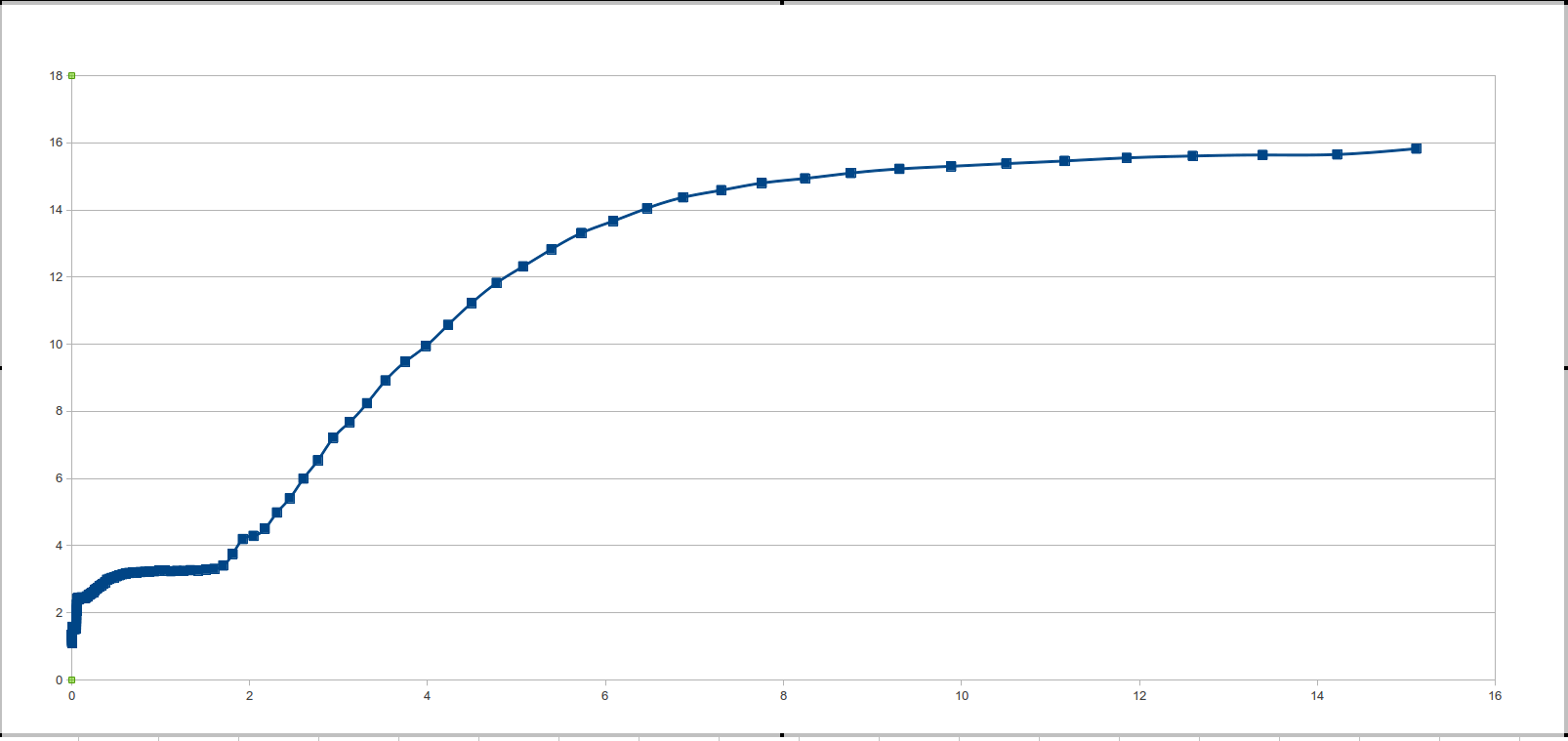
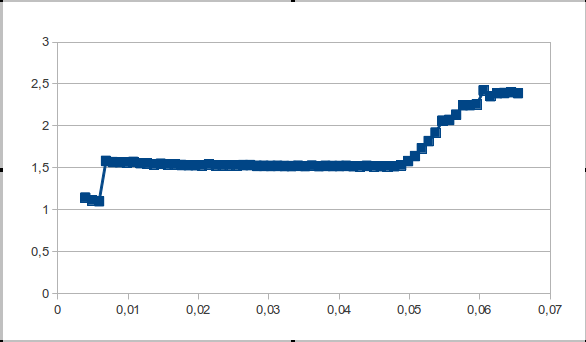
Программа разбита на 2 части — тест и обработка данных. Написать скрипт в 3 строки для запуска или 2 раза запустить ручками решайте сами.
Листинг файла size.с Linux
Листинг файла size.с Windows
В общем- то думаю все понятно, но хотелось бы оговорить несколько моментов.
Массив A объявлен как volatile — эта директива гарантирует нам что к массиву A всегда будут обращения, то-есть их не «вырежут» ни оптимизатор, ни компилятор. Так-же стоит оговорить то что вся вычислительная нагрузка выполняется до замера времени, что позволяет нам, уменьшить фоновое влияние.
Файл переведен в ассемблер на Ubuntu 12.04 и компилятором gcc 4.6 — циклы сохраняются.
Для обработки данных логично использовать производные. И несмотря на то что с повышением порядка дифференцирования шумы возрастают, будет использована вторая производная и её свойства. Как бы не была зашумлена вторая производная, нас интересует лишь знак второй производной.
Находим все точки, в которых вторая производная больше нуля (с некоторой погрешностью потому-что вторая производная, помимо того что считается численно, — сильно зашумлена ). Задаем функцию зависимости знака второй производной функции от размера кэша. Функция принимает значение 1 в точках, где знак второй производной больше нуля, и ноль, если знак второй производной меньше или равен нулю.
Точки «взлетов» — начало каждой ступеньки. Также перед обработкой данных нужно убрать одиночные выбросы, которые не меняют смысловой нагрузки данных, но создают ощутимый шум.
Листинг файла data_pr.с
CPU/ОС/версия ядра/компилятор/ключи компиляции — будут указаны для каждого теста.
Грабля обнаружилась при обработке данных на серверном процессоре Intel Xeon 2.4/L2 = 512 кб/Windows Server 2008
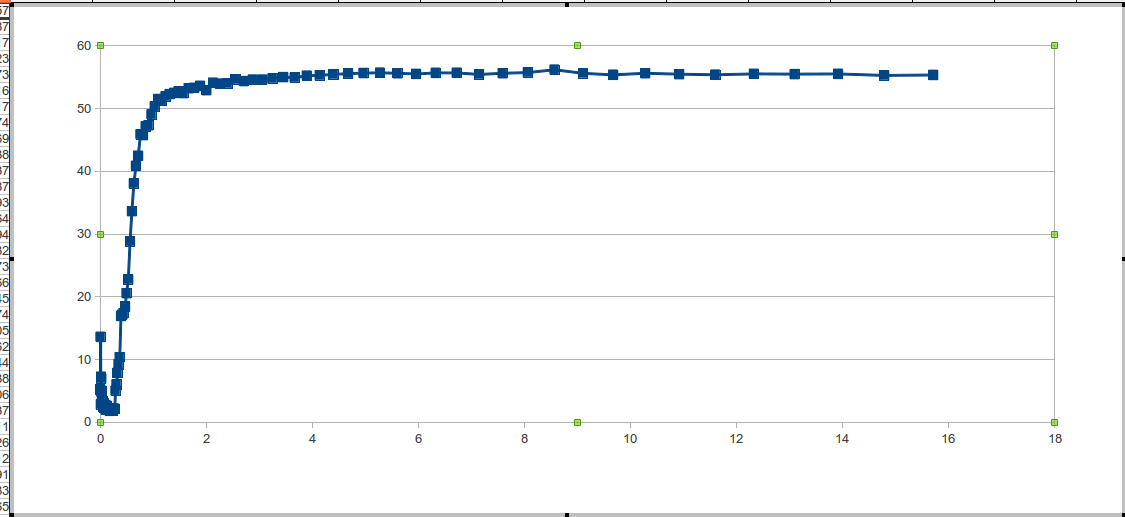
Проблема заключается в маленьком количестве точек, попадающих на интервал выхода на плато, — соответственно, скачок второй производной незаметен и принимается за шум.
Можно решить эту проблему методом наименьших квадратов, либо прогонять тесты в по ходу определения зон плато.
Хотелось бы услышать ваши предложения, по поводу решения этой проблемы.
Скорость и частота работы памяти — это то основное за счет чего мы получаем «свой кусок бесплатного торта» (ссылка). Именно поэтому важно использовать память, настолько эффективно, насколько мы можем это делать, а тем более такую быструю как кэш. Для оптимизации программы под конкретный компьютер, полезно знать характеристики кэш-памяти процессора: количество уровней, размер, длину строки. Особенно это важно в высокопроизводительном коде — ядра систем, математические библиотеки.
Как же определить характеристики кэша автоматический? (естественно cpuinfo распарсить не считается, хотя-бы потому-что в конечном итоге мы бы хотели получить алгоритм, который можно без труда реализовать в других ОС. Удобно, не правда ли? ) Именно этим мы сейчас и займемся.
Немного теории
В данный момент существуют и широко используются три разновидности кэш-памяти: кэш с прямым отображением, ассоциативный кэш и множественно-ассоциативный кэш.
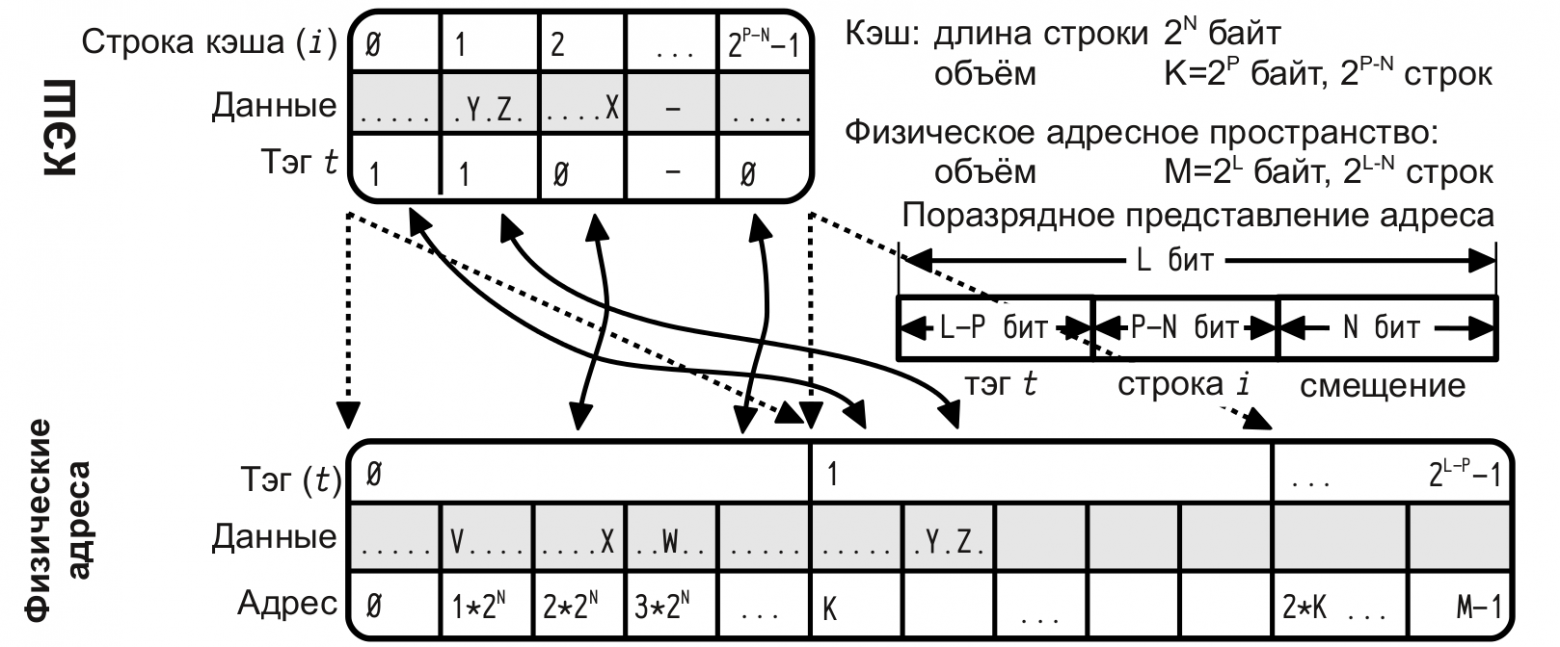
Кэш с прямым отображением (direct mapping cache)
— данная строка ОЗУ может быть отображена в единственную строку кэша, но в каждую строку кэша может быть отображено много возможных строк ОЗУ.
Ассоциативный кэш (fully associative cache)
— любая строка ОЗУ может быть отображена в любую строку кэша.
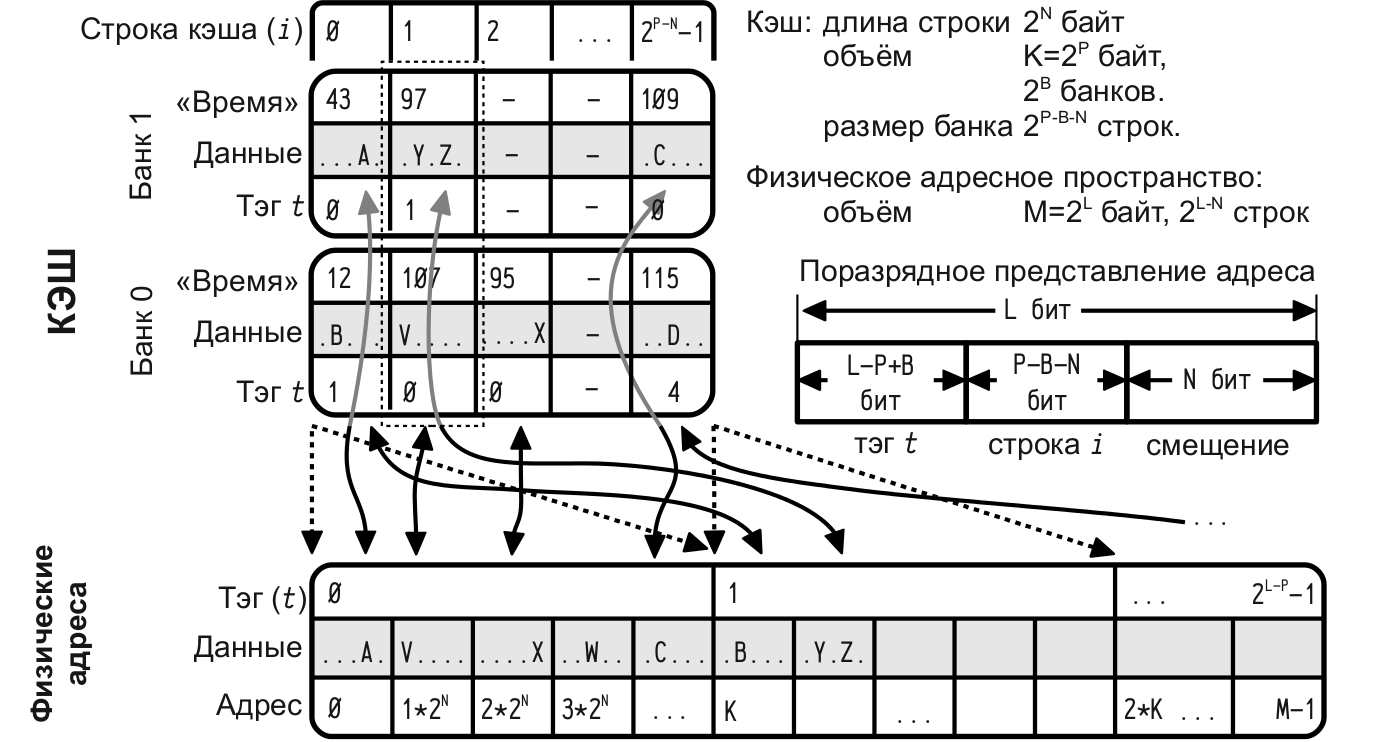
Множественно-ассоциативный кэш
— кэш-память делится на несколько «банков», каждый из которых функционирует как кэш с прямым отображением, таким образом строка ОЗУ может быть отображена не в единственную возможную запись кэша (как было бы в случае прямого отображения), а в один из нескольких банков; выбор банка осуществляется на основе LRU или иного механизма для каждой размещаемой в кэше строки.
LRU — вытеснение самой «долго не использованной» строки, кэш памяти.
Идея
Чтобы определить количество уровней кэша нужно рассмотреть порядок обращений к памяти, на котором будет четко виден переход. Разные уровни кэша отличаются прежде всего скоростью отклика памяти. В случае «кэш-промаха» для кэша L1 будет произведен поиск данных в следующих уровнях памяти, при этом если размер данных больше L1 и меньше L2 — то скоростью отклика памяти будет скорость отклика L2. Предыдущее утверждение так же верно в общем случаи.
Ясно что нужно подобрать тест на котором, мы будем четко видеть кэш промахи и протестировать его на различных размерах данных.
Зная логику множественно-ассоциативных кэшей, работающих по алгоритму LRU не трудно придумать алгоритм на котором кэш «валится», ничего хитрого — проход по строке. Критерием эффективности будем считать время одного обращения к памяти. Естественно нужно последовательно обращаться ко всем элементам строки, повторяя многократно для усреднения результата. К примеру возможны случаи, когда строка умещается в кэше но для первого прохода мы грузим строку из оперативной памяти и потому получаем совсем неадекватное время.
Хочется увидеть что-то подобное ступенькам, проходя по строкам разной длины. Для определения характера ступенек рассмотрим пример прохода по строке для прямого и ассоциативного кэша, случай с множественно-ассоциативным кэшем будет среднем между кэшем с прямым отображением и ассоциативным кэшем.
Ассоциативный кэш
Как только размер данных превышает размер кэш-памяти,
полностью ассоциативный кэш «промахивается» при каждом обращении к памяти.

Прямой кэш
Рассмотрим разные размеры строк. — показывает максимальное количество промахов, которое потратит процессор для доступа к элементам массива при следующем проходе по строке.




Как видно время доступа к памяти возрастает не резко, а по мере увеличения объема данных. Как только размер данных превысит размер кэша, то промахи будут при каждом обращении к памяти.
Потому у ассоциативного кэша ступенька будет вертикальной, а у прямого — плавно возрастать вплоть до двойного размера кэша. Множественно ассоциативный кэш будет средним случаем, «бугорком», хотя бы потому, что время-доступа не может быть лучше прямого.
Если-же говорить о памяти — то самая быстрая это кэш, следом идет оперативная, самая медленная это swap, про него мы в дальнейшем говорить не будем. В свою очередь у разных уровней кэша (как правило сегодня процессоры имеют 2-3 уровня кэша) разная скорость отклика памяти: чем больше уровень, тем меньше скорость отклика. И поэтому, если строка помещается в первый уровень кэша, (который кстати полностью ассоциативный) время отклика будет меньше, чем у строки значительно превышающей размеры кэша первого уровня. По-этому на графике времени отклика памяти от размеров строки будет несколько плато — плато* отклика памяти, и плато вызванные различными уровнями кэша.
*Плато функции — { i:x, f(xi) — f(xi+1) < eps: eps → 0 }
Приступим к реализации
Для реализации будем использовать Си (ANSI C99).
Быстро написан код, обычный проход по строкам разной длины, меньше 10мб, выполняющийся многократно. (Будем приводить небольшие куски программы, несущие смысловую нагрузку).
for (i = 0; i < 16; i++) {
for (j = 0; j < L_STR; j++) A[j]++;
}
Смотрим на график — и видим одну большую ступеньку. Но ведь в теории получается все, просто замечательно. Стало быть нужно понять: из за чего это происходит? И как это исправить?

Очевидно что это может происходить по двум причинам: либо в процессоре нет кэш памяти, либо процессор так хорошо угадывает обращения к памяти. Поскольку первый вариант ближе к фантастике причина всему хорошее предсказание обращений.
Дело в том, что сегодня далеко не топовые процессоры, помимо принципа пространственной локальности, предсказывают также и арифметическую прогрессию в порядке обращения к памяти. Поэтому нужно рандомизовать обращения к памяти.
Длина рандомизованного массива должна быть сопоставимой с длиной основной строки, чтобы избавиться от большой гранулярности обращений, так же длина массива не должна быть степенью двойки, из-за этого происходили «наложения» — следствием чего могут — быть выбросы. Лучше всего задать гранулярность константно, в том числе, если гранулярность простое число, то можно избежать эффектов наложений. А длина рандомиованого массива — функция от длинны строки.
for (i = 0; i < j; i++) {
for (m = 0; m < L; m++) {
for (x = 0; x < M; x++){
v = A[ random[x] + m ];
}
}
}
После чего мы удивили столь долгожданную «картинку», о которой говорили в начале.


Программа разбита на 2 части — тест и обработка данных. Написать скрипт в 3 строки для запуска или 2 раза запустить ручками решайте сами.
Листинг файла size.с Linux
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#define T char
#define MAX_S 0x1000000
#define L 101
volatile T A[MAX_S];
int m_rand[0xFFFFFF];
int main (){
static struct timespec t1, t2;
memset ((void*)A, 0, sizeof (A));
srand(time(NULL));
int v, M;
register int i, j, k, m, x;
for (k = 1024; k < MAX_S;) {
M = k / L;
printf("%g\t", (k+M*4)/(1024.*1024));
for (i = 0; i < M; i++) m_rand[i] = L * i;
for (i = 0; i < M/4; i++) {
j = rand() % M;
x = rand() % M;
m = m_rand[j];
m_rand[j] = m_rand[i];
m_rand[i] = m;
}
if (k < 100*1024) j = 1024;
else if (k < 300*1024) j = 128;
else j = 32;
clock_gettime (CLOCK_PROCESS_CPUTIME_ID, &t1);
for (i = 0; i < j; i++) {
for (m = 0; m < L; m++) {
for (x = 0; x < M; x++){
v = A[ m_rand[x] + m ];
}
}
}
clock_gettime (CLOCK_PROCESS_CPUTIME_ID, &t2);
printf ("%g\n",1000000000. * (((t2.tv_sec + t2.tv_nsec * 1.e-9) - (t1.tv_sec + t1.tv_nsec * 1.e-9)))/(double)(L*M*j));
if (k > 100*1024) k += k/16;
else k += 4*1024;
}
return 0;
}
Листинг файла size.с Windows
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#include <iostream>
#include <Windows.h>
using namespace std;
#define T char
#define MAX_S 0x1000000
#define L 101
volatile T A[MAX_S];
int m_rand[0xFFFFFF];
int main (){
LARGE_INTEGER freq; LARGE_INTEGER time1; LARGE_INTEGER time2;
QueryPerformanceFrequency(&freq);
memset ((void*)A, 0, sizeof (A));
srand(time(NULL));
int v, M;
register int i, j, k, m, x;
for (k = 1024; k < MAX_S;) {
M = k / L;
printf("%g\t", (k+M*4)/(1024.*1024));
for (i = 0; i < M; i++) m_rand[i] = L * i;
for (i = 0; i < M/4; i++) {
j = rand() % M;
x = rand() % M;
m = m_rand[j];
m_rand[j] = m_rand[i];
m_rand[i] = m;
}
if (k < 100*1024) j = 1024;
else if (k < 300*1024) j = 128;
else j = 32;
QueryPerformanceCounter(&time1);
for (i = 0; i < j; i++) {
for (m = 0; m < L; m++) {
for (x = 0; x < M; x++){
v = A[ m_rand[x] + m ];
}
}
}
QueryPerformanceCounter(&time2);
time2.QuadPart -= time1.QuadPart;
double span = (double) time2.QuadPart / freq.QuadPart;
printf ("%g\n",1000000000. * span/(double)(L*M*j));
if (k > 100*1024) k += k/16;
else k += 4*1024;
}
return 0;
}В общем- то думаю все понятно, но хотелось бы оговорить несколько моментов.
Массив A объявлен как volatile — эта директива гарантирует нам что к массиву A всегда будут обращения, то-есть их не «вырежут» ни оптимизатор, ни компилятор. Так-же стоит оговорить то что вся вычислительная нагрузка выполняется до замера времени, что позволяет нам, уменьшить фоновое влияние.
Файл переведен в ассемблер на Ubuntu 12.04 и компилятором gcc 4.6 — циклы сохраняются.
Обработка данных
Для обработки данных логично использовать производные. И несмотря на то что с повышением порядка дифференцирования шумы возрастают, будет использована вторая производная и её свойства. Как бы не была зашумлена вторая производная, нас интересует лишь знак второй производной.
Находим все точки, в которых вторая производная больше нуля (с некоторой погрешностью потому-что вторая производная, помимо того что считается численно, — сильно зашумлена ). Задаем функцию зависимости знака второй производной функции от размера кэша. Функция принимает значение 1 в точках, где знак второй производной больше нуля, и ноль, если знак второй производной меньше или равен нулю.
Точки «взлетов» — начало каждой ступеньки. Также перед обработкой данных нужно убрать одиночные выбросы, которые не меняют смысловой нагрузки данных, но создают ощутимый шум.
Листинг файла data_pr.с
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
double round (double x)
{
int mul = 100;
if (x > 0)
return floor(x * mul + .5) / mul;
else
return ceil(x * mul - .5) / mul;
}
float size[112], time[112], der_1[112], der_2[112];
int main(){
size[0] = 0; time[0] = 0; der_1[0] = 0; der_2[0] = 0;
int i, z = 110;
for (i = 1; i < 110; i++)
scanf("%g%g", &size[i], &time[i]);
for (i = 1; i < z; i++)
der_1[i] = (time[i]-time[i-1])/(size[i]-size[i-1]);
for (i = 1; i < z; i++)
if ((time[i]-time[i-1])/(size[i]-size[i-1]) > 2)
der_2[i] = 1;
else
der_2[i] = 0;
//comb
for (i = 0; i < z; i++)
if (der_2[i] == der_2[i+2] && der_2[i+1] != der_2[i]) der_2[i+1] = der_2[i];
for (i = 0; i < z-4; i++)
if (der_2[i] == der_2[i+3] && der_2[i] != der_2[i+1] && der_2[i] != der_2[i+2]) {
der_2[i+1] = der_2[i]; der_2[i+2] = der_2[i];
}
for (i = 0; i < z-4; i++)
if (der_2[i] == der_2[i+4] && der_2[i] != der_2[i+1] && der_2[i] != der_2[i+2] && der_2[i] != der_2[i+3]) {
der_2[i+1] = der_2[i]; der_2[i+2] = der_2[i]; der_2[i+3] = der_2[i];
}
//
int k = 1;
for (i = 0; i < z-4; i++){
if (der_2[i] == 1) printf("L%d = %g\tMb\n", k++, size[i]);
while (der_2[i] == 1) i++;
}
return 0;
}
Тесты
CPU/ОС/версия ядра/компилятор/ключи компиляции — будут указаны для каждого теста.
-
Intel Pentium CPU P6100 @2.00GHz / Ubuntu 12.04 / 3.2.0-27-generic / gcc -Wall -O3 size.c -lrt
L1 = 0.05 Mb
L2 = 0.2 Mb
L3 = 2.7 Mb
- Не буду приводить все хорошие тесты, давайте лучше поговорим о «Граблях»
Давайте поговорим о «граблях»
Грабля обнаружилась при обработке данных на серверном процессоре Intel Xeon 2.4/L2 = 512 кб/Windows Server 2008

Проблема заключается в маленьком количестве точек, попадающих на интервал выхода на плато, — соответственно, скачок второй производной незаметен и принимается за шум.
Можно решить эту проблему методом наименьших квадратов, либо прогонять тесты в по ходу определения зон плато.
Хотелось бы услышать ваши предложения, по поводу решения этой проблемы.
Список литературы
- Макаров А.В. Архитектура ЭВМ и Низкоуровневое программирование.
- Ulrich Drepper What every programmer should know about memory