Поворот растрового изображения на углы, кратные 90°, относительно геометрического центра изображения – задача тривиальная и решается без потери качества простым преобразованием координат каждого пикселя.
Для поворота растрового изображения на произвольный угол разработаны быстрые но не оптимальные алгоритмы, дающие приемлемую для практических целей аппроксимацию с потерей качества (например, этот).
 Довольно давно, из чисто спортивного интереса, меня заинтересовала задача максимально точного поворота растрового изображения на произвольный угол. К сожалению, мне нигде не удалось найти готовый алгоритм, поэтому пришлось делать его собственноручно. Даже если в итоге я «изобрёл велосипед», результат, как мне кажется, получился достаточно интересным, чтобы им можно было поделиться.
Довольно давно, из чисто спортивного интереса, меня заинтересовала задача максимально точного поворота растрового изображения на произвольный угол. К сожалению, мне нигде не удалось найти готовый алгоритм, поэтому пришлось делать его собственноручно. Даже если в итоге я «изобрёл велосипед», результат, как мне кажется, получился достаточно интересным, чтобы им можно было поделиться.
Ниже мы рассмотрим алгоритм прецизионного поворота растрового изображения на произвольный угол относительно произвольного центра с минимальными потерями.
Выражаю благодарность Харченко Владиславу Владимировичу за оказанную помощь.
Из вышеприведённого рисунка видно, что после поворота растрового изображения, цвет каждого пикселя итогового изображения определяется сложением цветов нескольких «осколков» нескольких пикселей исходного изображения, пропорционально площадям соответствующих «осколков». Поэтому в общем виде решение нашей задачи будет состоять в том, чтобы найти площади всех «осколков» для каждого пикселя исходного изображения и собрать цвет каждого пикселя итогового изображения из цветов соответствующих «осколков».
В качестве модели пикселя исходного изображения мы будем использовать квадрат со стороной = 1, с такими обозначениями углов:
 i1 — самый правый угол;
i1 — самый правый угол;
i2 — самый нижний угол;
i3 — самый левый угол;
i4 — самый верхний угол.
Моделью итогового изображения будет сетка из параллельных горизонтальных и вертикальных линий с расстоянием между линиями = 1.
Координаты центра поворота растрового изображения, в таком представлении, могут быть выражены парой произвольных вещественных чисел. То есть центр поворота в нашей задаче может лежать не в геометрическом центре пикселя и не в точке пересечения линий сетки, а в произвольной точке декартовых координат.
Поскольку при повороте растрового изображения квадрат каждого пикселя поворачивается на один и тот же угол (относительно центра этого пикселя) мы будем решать задачу для одного пикселя, а потом применим полученное решение для каждого пикселя исходного изображения.
Поворот растрового изображения можно разделить на две части:
1. Поворот квадрата каждого пикселя исходного изображения относительно центра этого квадрата на заданный угол.
2. Смещение центра квадрата пикселя в соответствии с углом поворота изображения относительно центра поворота изображения таким образом, чтобы квадрат занял своё итоговое положение на сетке итогового изображения.
При этом сетка итогового изображения рассекает квадрат каждого пикселя исходного изображения на «осколки» в количестве 4, 5 или 6 штук.
Чтобы систематизировать разнообразие получающихся вариантов мне пришлось составить таксономию всевозможных пересечений квадрата пикселя исходного изображения с сеткой итогового изображения. Существенно разных вариантов оказалось всего 23:

Условные обозначения здесь следующие:
— цифры в ячейках обозначают номера углов квадрата пикселя, которые попали в данную ячейку сетки итогового изображения после поворота изображения;
— зелёным цветом обозначены ячейки, в которые попали участки пикселя и гарантированно оставили там по «осколку»;
— жёлтым цветом обозначены ячейки, в которые, в зависимости от условий, могут попасть (а могут и не попасть) «осколки» квадрата пикселя, образованные не углами квадрата, а сторонами квадрата.
Для наглядности приведу одну из возможных вариаций варианта №3:
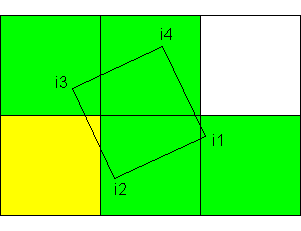
Как видим, верхняя правая ячейка не содержит в себе «осколка» пикселя, хотя при других условиях поворота могла бы содержать.
Чтобы не нагружать читателя детальными геометрическими выкладками, скажу сразу, что во всех этих 23-х вариантах пиксель исходного изображения рассекается на «осколки», площадь которых легко вычисляется комбинированием 4-х формул. Ниже приведены эти формулы с иллюстрациями. Красным цветом обозначены линии сетки итогового изображения, которые рассекают квадрат пикселя. Жёлтым цветом закрашена область, площадь которой вычисляется формулой.
 Эта формула не используется для расчёта окончательной площади «осколка», но её удобно использовать для быстрого расчёта вспомогательных промежуточных площадей, поскольку нам заведомо известно, что площадь всего пикселя = 1.
Эта формула не используется для расчёта окончательной площади «осколка», но её удобно использовать для быстрого расчёта вспомогательных промежуточных площадей, поскольку нам заведомо известно, что площадь всего пикселя = 1.
В качестве входных переменных во всех формулах используются высоты, опущенные из углов квадрата на сетку итогового изображения, по той простой причине, что расчёт этих высот сводится к мгновенному выделению дробной части числового значения координаты соответствующего угла квадрата пикселя.
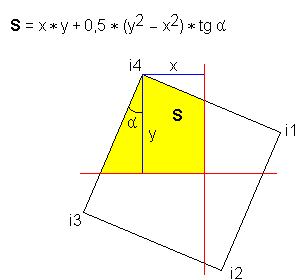
Данная формула используется только в вариантах 1 и 2.
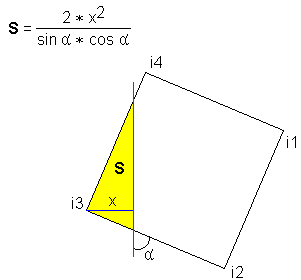 Часто используемая формула — очень хорошо, что она быстро вычисляется. Поскольку угол поворота одинаков для каждого пикселя — все тригонометрические функции можно посчитать один раз, перед обработкой всех пикселей, и далее использовать эти значения в цикле как константы.
Часто используемая формула — очень хорошо, что она быстро вычисляется. Поскольку угол поворота одинаков для каждого пикселя — все тригонометрические функции можно посчитать один раз, перед обработкой всех пикселей, и далее использовать эти значения в цикле как константы.
 Эта формула вычисляется в два этапа. Сначала вычисляется выражение в скобках. Если оно принимает положительное значение, то вычисляется площадь. Если значение отрицательное, значит от пикселя не отсекается «осколок», образованный углом сетки и стороной квадрата и дальнейшие вычисления производить не имеет смысла.
Эта формула вычисляется в два этапа. Сначала вычисляется выражение в скобках. Если оно принимает положительное значение, то вычисляется площадь. Если значение отрицательное, значит от пикселя не отсекается «осколок», образованный углом сетки и стороной квадрата и дальнейшие вычисления производить не имеет смысла.
С учётом всего вышесказанного, в общем виде алгоритм будет выглядеть так:
1. Загружаем в память ЭВМ исходное изображение.
2. Рассчитываем размеры итогового изображения в пикселях.
3. Создаём промежуточный двумерный массив, каждый элемент которого содержит 3 составляющие цвета RGB в формате числа с плавающей запятой. Размеры массива равны размерам итогового изображения.
4. Последовательно перебираем все пиксели исходного изображения; поворачиваем каждый из них на заданный угол и располагаем на сетке итогового изображения, рассчитав 4 координаты углов квадрата пикселя; классифицируем пиксель по 23 вариантам и считаем площади «осколков»; добавляем в соответствующие элементы промежуточного массива цвета полученных «осколков» пропорционально площади этих «осколков».
5. После обработки всех пикселей исходного изображения округляем значения RGB в промежуточном массиве до целого значения для каждого элемента и создаём на базе этих целых значений итоговое изображение в формате BMP.
На основании приведённого алгоритма была написана программа для Windows. Исходные коды на Object Pascal и скомпилированный исполняемый файл можно скачать здесь.
Интерфейс программы.
По нажатию на кнопку «Open...» открывается диалог выбора BMP-файла. Поддерживаются битмапы только с 24-битной палитрой. Открытое изображение отображается в окне. В заголовке окна выводится полный путь к файлу и размеры изображения.
В поле «Angle» задаётся угол поворота в градусах – любое положительное число.
В качестве десятичного разделителя при вводе дробных чисел может быть использована как точка, так и запятая.
Радиокнопками «CW» и «CCW» задаётся направление вращения: «по часовой стрелке» и «против часовой стрелки», соответственно.
В блоке «Background color» можно задать цвет фона, с которым будут смешиваться граничные пиксели изображения. По умолчанию цвет фона – чёрный.
В полях «Centre X» и «Centre Y» задаются координаты центра поворота. При этом следует учитывать, что начало координат находится в левом верхнем углу изображения и Y увеличивается вниз. По умолчанию центр поворота устанавливается в геометрическом центре загруженного изображения.
По нажатию на кнопку «Rotate» либо по нажатию на клавишу Enter изображение поворачивается на заданный угол относительно заданного центра поворота и отображается в окне. Поворот изображения на углы, кратные 90°, реализован по упрощённой схеме, путём простого преобразования координат пикселей исходного изображения, при этом значения «Centre X» и «Centre Y» игнорируются.
Время работы алгоритма в секундах отображается под кнопкой «Rotate».
Через кнопку «Save…» повёрнутое изображение можно сохранить в BMP-файл.
Если итоговое изображение не помещается в окне – оно подгоняется к границам окна API-функцией StretchBlt – поэтому оценить реальное качество больших картинок можно только по сохранённому BMP-файлу.
Для поворота изображения на другой угол его не нужно загружать повторно — поворачивается изображение из выбранного файла, а не отображённое в данный момент в окне.
Изображение с размерами 1024 х 768 на машине с четырёхядерным процессором 2,67 ГГц поворачивается данной программой на произвольный угол, в среднем, приблизительно, за 0,5 секунды. Изображение с размерами 4000 х 4000 — примерно за 10 секунд. Время работы алгоритма для разных углов может отличаться в связи с тем, что изображение при разных углах дробится на разное количество «осколков», на вычисление площадей которых суммарно тратится, соответственно, разное время.
Промежуточный массив, содержащий информацию о цвете пикселей итогового изображения в формате числа с плавающей запятой, реализован на типе extended (10 байт), поэтому обработка больших изображений (примерно более 5000 х 5000 пикселей) может вызвать ошибку переполнения памяти. Улучшить ситуацию возможно, применив менее точный тип данных и сохраняя целую часть числа сразу в итоговый битмап, оставляя во вспомогательном массиве только дробную часть.
Проведём сравнительный анализ работы прецизионного алгоритма и алгоритма поворота изображений, реализованного в программе Photoshop.
Для первого теста я взял очень простое изображение — горизонтальную линию чёрного цвета толщиной 1 пиксель и длиной 10 пикселей, смещённую относительно центра белого квадрата с размерами 100 х 100 пикселей:

После чего я повернул данное изображение относительно точки с координатами (0, 0) на 3° по часовой стрелке. Точка (0, 0) выбрана потому, что, судя по моим экспериментам, Photoshop поворачивает изображение относительно именно этой точки. Вот сравнительный результат (увеличено в 24 раза):
Прецизионный алгоритм
Photoshop 7.0.1
Photoshop CS6 (64 Bit)
Алгоритм Photoshop даёт более контрастную картинку, прецизионный алгоритм несколько «размывает» изображение. Но в целом, при визуальной оценке, результат получается почти одинаковым. Попутно отметим, что алгоритм поворота, реализованный в Photoshop, не претерпел за 10 лет существенных изменений.
Для второго теста я выбрал тюльпан из стандартного дистрибутива Win7:

После поворота данного изображения на 5° по часовой стрелке относительно геометрического центра я суммировал цвет всех пикселей в разрезе каналов RGB. Вот результат для прецизионного алгоритма и алгоритма Photoshop:
Числа в скобках показывают абсолютное отклонение данного показателя от оригинала.
Цвет изображения после прецизионного поворота и до округления практически не поменялся — чего и следовало ожидать.
Самое большое отклонение, в данном конкретном случае, мы обнаруживаем по каналу G для алгоритма Photoshop. В процентном отношении это отклонение составляет всего 0,06%, поэтому «на глаз» оно не заметно, но из соображений перфекционизма результат у Photoshop получается хуже, чем у прецизионного алгоритма.
Важно отметить, что округление цвета каждого пикселя в прецизионном алгоритме до целочисленного значения, необходимого для формата BMP, необратимо уничтожает часть информации о цвете.
Для визуального сравнения двух алгоритмов приведу увеличенный фрагмент изображения,

повёрнутого на 5° по часовой стрелке, соответственно, Photoshop'ом:

и прецизионным алгоритмом:

Сравнительный анализ показывает, что Photoshop лучше сохраняет контрастные элементы изображения, но при этом создаёт «ореолы» искажённого цвета. Прецизионный алгоритм не искажает цвет но при этом несколько «размывает» изображение.
1. Прецизионный и при этом сравнительно быстрый поворот растрового изображения на произвольный угол — возможен. Для меня остаётся загадкой вопрос, почему в профессиональных графических редакторах нет опции, позволяющей пользователю повернуть изображение предельно точно за чуть большее время.
2. Несмотря на предельную точность рассмотренного алгоритма, обратное преобразование изображения, т.е. поворот на противоположный угол без потери качества — невозможен, потому что округление точного значения цвета (в формате числа с плавающей запятой) необратимо уничтожает часть информации о цвете.
3. С точки зрения визуального восприятия контрастных деталей лучший результат даёт подоптимальный алгоритм Photoshop. Прецизионный же алгоритм имеет смысл применять в тех случаях, когда важно сохранить максимум информации о цвете изображения.
UPD: Для практического использования написал программу, реализующую упрощённый алгоритм, в котором для каждого пикселя итогового изображения все необходимые кусочки пикселей исходного изображения рассчитываются последовательно и округление цвета происходит немедленно. Только после этого рассчитывается следующий пиксель итогового изображения. При этом к отдельному пикселю исходного изображения программа обращается несколько раз. Время расчётов, таким образом, увеличилось, в среднем, в 1,7 раз, но память в этой версии алгоритма расходуется только на хранение битмапов, что позволяет работать с изображениями больших размеров. Скачать программу и исходники можно здесь.
Для поворота растрового изображения на произвольный угол разработаны быстрые но не оптимальные алгоритмы, дающие приемлемую для практических целей аппроксимацию с потерей качества (например, этот).
 Довольно давно, из чисто спортивного интереса, меня заинтересовала задача максимально точного поворота растрового изображения на произвольный угол. К сожалению, мне нигде не удалось найти готовый алгоритм, поэтому пришлось делать его собственноручно. Даже если в итоге я «изобрёл велосипед», результат, как мне кажется, получился достаточно интересным, чтобы им можно было поделиться.
Довольно давно, из чисто спортивного интереса, меня заинтересовала задача максимально точного поворота растрового изображения на произвольный угол. К сожалению, мне нигде не удалось найти готовый алгоритм, поэтому пришлось делать его собственноручно. Даже если в итоге я «изобрёл велосипед», результат, как мне кажется, получился достаточно интересным, чтобы им можно было поделиться.Ниже мы рассмотрим алгоритм прецизионного поворота растрового изображения на произвольный угол относительно произвольного центра с минимальными потерями.
Выражаю благодарность Харченко Владиславу Владимировичу за оказанную помощь.
Алгоритм
Из вышеприведённого рисунка видно, что после поворота растрового изображения, цвет каждого пикселя итогового изображения определяется сложением цветов нескольких «осколков» нескольких пикселей исходного изображения, пропорционально площадям соответствующих «осколков». Поэтому в общем виде решение нашей задачи будет состоять в том, чтобы найти площади всех «осколков» для каждого пикселя исходного изображения и собрать цвет каждого пикселя итогового изображения из цветов соответствующих «осколков».
В качестве модели пикселя исходного изображения мы будем использовать квадрат со стороной = 1, с такими обозначениями углов:
 i1 — самый правый угол;
i1 — самый правый угол;i2 — самый нижний угол;
i3 — самый левый угол;
i4 — самый верхний угол.
Моделью итогового изображения будет сетка из параллельных горизонтальных и вертикальных линий с расстоянием между линиями = 1.
Координаты центра поворота растрового изображения, в таком представлении, могут быть выражены парой произвольных вещественных чисел. То есть центр поворота в нашей задаче может лежать не в геометрическом центре пикселя и не в точке пересечения линий сетки, а в произвольной точке декартовых координат.
Поскольку при повороте растрового изображения квадрат каждого пикселя поворачивается на один и тот же угол (относительно центра этого пикселя) мы будем решать задачу для одного пикселя, а потом применим полученное решение для каждого пикселя исходного изображения.
Поворот растрового изображения можно разделить на две части:
1. Поворот квадрата каждого пикселя исходного изображения относительно центра этого квадрата на заданный угол.
2. Смещение центра квадрата пикселя в соответствии с углом поворота изображения относительно центра поворота изображения таким образом, чтобы квадрат занял своё итоговое положение на сетке итогового изображения.
При этом сетка итогового изображения рассекает квадрат каждого пикселя исходного изображения на «осколки» в количестве 4, 5 или 6 штук.
Чтобы систематизировать разнообразие получающихся вариантов мне пришлось составить таксономию всевозможных пересечений квадрата пикселя исходного изображения с сеткой итогового изображения. Существенно разных вариантов оказалось всего 23:

Условные обозначения здесь следующие:
— цифры в ячейках обозначают номера углов квадрата пикселя, которые попали в данную ячейку сетки итогового изображения после поворота изображения;
— зелёным цветом обозначены ячейки, в которые попали участки пикселя и гарантированно оставили там по «осколку»;
— жёлтым цветом обозначены ячейки, в которые, в зависимости от условий, могут попасть (а могут и не попасть) «осколки» квадрата пикселя, образованные не углами квадрата, а сторонами квадрата.
Для наглядности приведу одну из возможных вариаций варианта №3:

Как видим, верхняя правая ячейка не содержит в себе «осколка» пикселя, хотя при других условиях поворота могла бы содержать.
Чтобы не нагружать читателя детальными геометрическими выкладками, скажу сразу, что во всех этих 23-х вариантах пиксель исходного изображения рассекается на «осколки», площадь которых легко вычисляется комбинированием 4-х формул. Ниже приведены эти формулы с иллюстрациями. Красным цветом обозначены линии сетки итогового изображения, которые рассекают квадрат пикселя. Жёлтым цветом закрашена область, площадь которой вычисляется формулой.
Формула 1
 Эта формула не используется для расчёта окончательной площади «осколка», но её удобно использовать для быстрого расчёта вспомогательных промежуточных площадей, поскольку нам заведомо известно, что площадь всего пикселя = 1.
Эта формула не используется для расчёта окончательной площади «осколка», но её удобно использовать для быстрого расчёта вспомогательных промежуточных площадей, поскольку нам заведомо известно, что площадь всего пикселя = 1.В качестве входных переменных во всех формулах используются высоты, опущенные из углов квадрата на сетку итогового изображения, по той простой причине, что расчёт этих высот сводится к мгновенному выделению дробной части числового значения координаты соответствующего угла квадрата пикселя.
Формула 2

Данная формула используется только в вариантах 1 и 2.
Формула 3
 Часто используемая формула — очень хорошо, что она быстро вычисляется. Поскольку угол поворота одинаков для каждого пикселя — все тригонометрические функции можно посчитать один раз, перед обработкой всех пикселей, и далее использовать эти значения в цикле как константы.
Часто используемая формула — очень хорошо, что она быстро вычисляется. Поскольку угол поворота одинаков для каждого пикселя — все тригонометрические функции можно посчитать один раз, перед обработкой всех пикселей, и далее использовать эти значения в цикле как константы.Формула 4
 Эта формула вычисляется в два этапа. Сначала вычисляется выражение в скобках. Если оно принимает положительное значение, то вычисляется площадь. Если значение отрицательное, значит от пикселя не отсекается «осколок», образованный углом сетки и стороной квадрата и дальнейшие вычисления производить не имеет смысла.
Эта формула вычисляется в два этапа. Сначала вычисляется выражение в скобках. Если оно принимает положительное значение, то вычисляется площадь. Если значение отрицательное, значит от пикселя не отсекается «осколок», образованный углом сетки и стороной квадрата и дальнейшие вычисления производить не имеет смысла.С учётом всего вышесказанного, в общем виде алгоритм будет выглядеть так:
1. Загружаем в память ЭВМ исходное изображение.
2. Рассчитываем размеры итогового изображения в пикселях.
3. Создаём промежуточный двумерный массив, каждый элемент которого содержит 3 составляющие цвета RGB в формате числа с плавающей запятой. Размеры массива равны размерам итогового изображения.
4. Последовательно перебираем все пиксели исходного изображения; поворачиваем каждый из них на заданный угол и располагаем на сетке итогового изображения, рассчитав 4 координаты углов квадрата пикселя; классифицируем пиксель по 23 вариантам и считаем площади «осколков»; добавляем в соответствующие элементы промежуточного массива цвета полученных «осколков» пропорционально площади этих «осколков».
5. После обработки всех пикселей исходного изображения округляем значения RGB в промежуточном массиве до целого значения для каждого элемента и создаём на базе этих целых значений итоговое изображение в формате BMP.
Программа
На основании приведённого алгоритма была написана программа для Windows. Исходные коды на Object Pascal и скомпилированный исполняемый файл можно скачать здесь.
Интерфейс программы.
По нажатию на кнопку «Open...» открывается диалог выбора BMP-файла. Поддерживаются битмапы только с 24-битной палитрой. Открытое изображение отображается в окне. В заголовке окна выводится полный путь к файлу и размеры изображения.
В поле «Angle» задаётся угол поворота в градусах – любое положительное число.
В качестве десятичного разделителя при вводе дробных чисел может быть использована как точка, так и запятая.
Радиокнопками «CW» и «CCW» задаётся направление вращения: «по часовой стрелке» и «против часовой стрелки», соответственно.
В блоке «Background color» можно задать цвет фона, с которым будут смешиваться граничные пиксели изображения. По умолчанию цвет фона – чёрный.
В полях «Centre X» и «Centre Y» задаются координаты центра поворота. При этом следует учитывать, что начало координат находится в левом верхнем углу изображения и Y увеличивается вниз. По умолчанию центр поворота устанавливается в геометрическом центре загруженного изображения.
По нажатию на кнопку «Rotate» либо по нажатию на клавишу Enter изображение поворачивается на заданный угол относительно заданного центра поворота и отображается в окне. Поворот изображения на углы, кратные 90°, реализован по упрощённой схеме, путём простого преобразования координат пикселей исходного изображения, при этом значения «Centre X» и «Centre Y» игнорируются.
Время работы алгоритма в секундах отображается под кнопкой «Rotate».
Через кнопку «Save…» повёрнутое изображение можно сохранить в BMP-файл.
Если итоговое изображение не помещается в окне – оно подгоняется к границам окна API-функцией StretchBlt – поэтому оценить реальное качество больших картинок можно только по сохранённому BMP-файлу.
Для поворота изображения на другой угол его не нужно загружать повторно — поворачивается изображение из выбранного файла, а не отображённое в данный момент в окне.
Изображение с размерами 1024 х 768 на машине с четырёхядерным процессором 2,67 ГГц поворачивается данной программой на произвольный угол, в среднем, приблизительно, за 0,5 секунды. Изображение с размерами 4000 х 4000 — примерно за 10 секунд. Время работы алгоритма для разных углов может отличаться в связи с тем, что изображение при разных углах дробится на разное количество «осколков», на вычисление площадей которых суммарно тратится, соответственно, разное время.
Промежуточный массив, содержащий информацию о цвете пикселей итогового изображения в формате числа с плавающей запятой, реализован на типе extended (10 байт), поэтому обработка больших изображений (примерно более 5000 х 5000 пикселей) может вызвать ошибку переполнения памяти. Улучшить ситуацию возможно, применив менее точный тип данных и сохраняя целую часть числа сразу в итоговый битмап, оставляя во вспомогательном массиве только дробную часть.
Результаты
Проведём сравнительный анализ работы прецизионного алгоритма и алгоритма поворота изображений, реализованного в программе Photoshop.
Тест 1
Для первого теста я взял очень простое изображение — горизонтальную линию чёрного цвета толщиной 1 пиксель и длиной 10 пикселей, смещённую относительно центра белого квадрата с размерами 100 х 100 пикселей:

После чего я повернул данное изображение относительно точки с координатами (0, 0) на 3° по часовой стрелке. Точка (0, 0) выбрана потому, что, судя по моим экспериментам, Photoshop поворачивает изображение относительно именно этой точки. Вот сравнительный результат (увеличено в 24 раза):
Прецизионный алгоритм
Photoshop 7.0.1
Photoshop CS6 (64 Bit)
Алгоритм Photoshop даёт более контрастную картинку, прецизионный алгоритм несколько «размывает» изображение. Но в целом, при визуальной оценке, результат получается почти одинаковым. Попутно отметим, что алгоритм поворота, реализованный в Photoshop, не претерпел за 10 лет существенных изменений.
Тест 2
Для второго теста я выбрал тюльпан из стандартного дистрибутива Win7:
После поворота данного изображения на 5° по часовой стрелке относительно геометрического центра я суммировал цвет всех пикселей в разрезе каналов RGB. Вот результат для прецизионного алгоритма и алгоритма Photoshop:
Оригинал |
Прецизионный поворот |
Прецизионный поворот |
Photoshop CS6 |
| R = 33381406 G = 27933900 B = 11239213 |
R = 33381406,0000004 (~0) G = 27933899,9999997 (~0) B = 11239212,9999999 (~0) |
R = 33382786 (1380) G = 27933920 (20) B = 11238086 (-1127) |
R = 33387726 (6320) G = 27950823 (16923) B = 11245937 (6724) |
Цвет изображения после прецизионного поворота и до округления практически не поменялся — чего и следовало ожидать.
Самое большое отклонение, в данном конкретном случае, мы обнаруживаем по каналу G для алгоритма Photoshop. В процентном отношении это отклонение составляет всего 0,06%, поэтому «на глаз» оно не заметно, но из соображений перфекционизма результат у Photoshop получается хуже, чем у прецизионного алгоритма.
Важно отметить, что округление цвета каждого пикселя в прецизионном алгоритме до целочисленного значения, необходимого для формата BMP, необратимо уничтожает часть информации о цвете.
Для визуального сравнения двух алгоритмов приведу увеличенный фрагмент изображения,
повёрнутого на 5° по часовой стрелке, соответственно, Photoshop'ом:

и прецизионным алгоритмом:

Сравнительный анализ показывает, что Photoshop лучше сохраняет контрастные элементы изображения, но при этом создаёт «ореолы» искажённого цвета. Прецизионный алгоритм не искажает цвет но при этом несколько «размывает» изображение.
Выводы
1. Прецизионный и при этом сравнительно быстрый поворот растрового изображения на произвольный угол — возможен. Для меня остаётся загадкой вопрос, почему в профессиональных графических редакторах нет опции, позволяющей пользователю повернуть изображение предельно точно за чуть большее время.
2. Несмотря на предельную точность рассмотренного алгоритма, обратное преобразование изображения, т.е. поворот на противоположный угол без потери качества — невозможен, потому что округление точного значения цвета (в формате числа с плавающей запятой) необратимо уничтожает часть информации о цвете.
3. С точки зрения визуального восприятия контрастных деталей лучший результат даёт подоптимальный алгоритм Photoshop. Прецизионный же алгоритм имеет смысл применять в тех случаях, когда важно сохранить максимум информации о цвете изображения.
UPD: Для практического использования написал программу, реализующую упрощённый алгоритм, в котором для каждого пикселя итогового изображения все необходимые кусочки пикселей исходного изображения рассчитываются последовательно и округление цвета происходит немедленно. Только после этого рассчитывается следующий пиксель итогового изображения. При этом к отдельному пикселю исходного изображения программа обращается несколько раз. Время расчётов, таким образом, увеличилось, в среднем, в 1,7 раз, но память в этой версии алгоритма расходуется только на хранение битмапов, что позволяет работать с изображениями больших размеров. Скачать программу и исходники можно здесь.