Все доброго времени суток!
Хочу рассказать об одной интересной проблеме и ее решении, которое я применил в одном из своих проектов.
Суть проблемы такова:
Есть несколько детекторов сигнала (допустим, базовые станции GSM). И эти детекторы присылают на сервер уровень сигнала для некоего источника. Необходимо вычислить и отобразить на карте координаты источника
Если вам интересно, как это сделать, добро пожаловать под кат.
Пусть, A(xa,ya), B(xb, yb), C(xc, yc) — детекторы сигнала с заданными координатами в некой прямоугольной системе координат. O(xo, yo) — источник сигнала.
Вспоминаем из школьного учебника физики, что амплитуда сигнала обратно пропорциональна квадрату расстояния до источника. Таким образом, расстояние Ra от источника O до детектора A будет равно
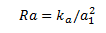
, где ka это некоторый коэффициент, который мы можем получить при калибровке устройств.
Формула для расчета расстояния a1 берем из школьного курса геометрии (стыдно ее тут приводить, но пусть будет для полноты).
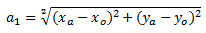
Гетерогенностью среды пренебрегаем. Да, это даст некоторую погрешность, но решение этой проблемы выходит за рамки задачи. Будем считать, что постоянные факторы, влияющие на распространение сигнала (наличие и материал стен, к примеру) — уже заложены в коэффициент ka. Факторы временные — интерференция, переотражение сигнала и т.п. — будут влиять на результат, но на практике даже в помещении мешают не очень сильно.
Таким образом, у нас есть формулы зависимости для расстояния от всех источников.
Если решать задачу «в лоб» — у нас есть система квадратных уравнений, решение которой даст нам точку с координатами xo, yo. Проблема в том, что университетский курс линейной алгебры я слегка подзабыл. После недели размышлений я наткнулся вот на такой способ.
Давайте нарисуем вокруг каждого детектора окружность, радиус которой обратно пропорционален уровню сигнала. Область пересечения всех окружностей и будет содержать источник сигнала. Для простоты – можно считать, что источник находится в центре этой области.
Строим чертеж для случая с тремя детекторами и одним источником.
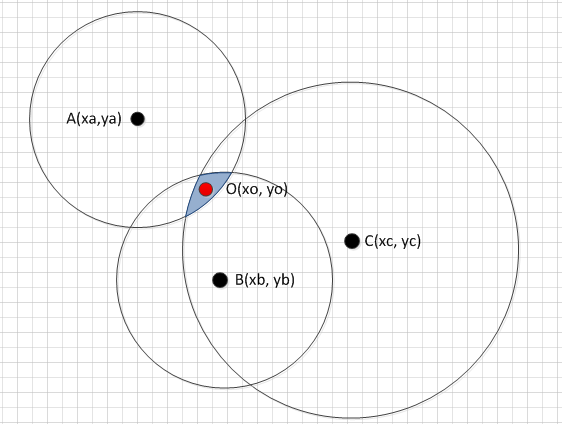
Здесь B и A ближе всего к источнику сигнала, поэтому диаметр окружности меньше. C дальше всех, диаметр больше. Зависимость диаметра окружности от уровня сигнала определяется экспериментально. Данный чертеж построен в реальных координатах (допустим, метры), для того, чтобы перейти к практике, переведем их в пиксели самым обычным образом. Нужно лишь знать размеры карты (ширина, высота) в пикселях и в метрах. Нелинейностью проекции (если это спутниковый снимок) как и прежде – пренебрегаем. Лучше использовать масштабную схему, в моем проекте это был план помещения.
Итак, простое решение найдено, попробуем его воплотить на практике. Серверная часть моего проекта разработана на Java, принимает данные от детекторов по TCP с SSL шифрованием в json формате. Эта часть кода независима, выполняется в отдельном потоке. Полученные события хранятся в базе mysql.
Триангуляция работает в своем потоке, выбирает еще не обработанные события из mysql базы (не позже, чем за 3 секунды до текущего времени – чтобы успеть получить сведения об этом же сигнале от всех источников).
Хотя решение получилось простым и не требует никакой математики, обсчитать пересечение окружностей тоже как-то надо. К счастью, в Java есть библиотека AWT, которая все за нас сделает. Отсутствие оконного интерфейса ее не смущает и отдельные ее классы прекрасно работают на сервере в backend-е.
Привожу немного упрощенный код из проекта.
Итак, ppx/ppy как вы поняли – это коэффициенты для перевода реальных координат в пиксели.
Берем уровень сигнала для первого детектора, вычисляем дистанцию до источника, строим окружность по известным нам координатам с полученным радиусом.
Теперь проходим по всем оставшимся источникам и делаем то же самое. Пересекаем первую окружность с получившейся, результат используем в цикле для оставшихся детекторов. Дополнительный трюк – пересекаем с прямоугольником помещения, иначе может так получиться, что результат выйдет за его пределы, что нам не нужно.
Ну и в конце концов проверяем, что у нас хоть что-то осталось в результате, плюс посчитаем погрешность вычисления (как половина диагонали прямоугольника, в который вписана полученная область).
Это функция вычисления расстояния.
Раньше это была логарифмическая функция, но, к сожалению, затухание реального сигнала отличается, пришлось в лаборатории посмотреть на уровень сигнала в нескольких точках и записать значения уровня сигнала и соответствующего расстояния в два массива.
Реальные цифры я на всякий случай убрал, чтобы не нарушить NDA.
Кстати, абсолютно такое же решение возможно на C#. Вместо Area нужно использовать GraphicsPath, там есть метод Intersect. Единственная сложность – поиск центра полученного пересечения. Вот код для поиска центра региона на C#:
Вот так, не обладая достаточными познаниями в математике и физике, с определенными допущениями, можно решить довольно сложную задачу.
Спасибо за внимание!
Хочу рассказать об одной интересной проблеме и ее решении, которое я применил в одном из своих проектов.
Суть проблемы такова:
Есть несколько детекторов сигнала (допустим, базовые станции GSM). И эти детекторы присылают на сервер уровень сигнала для некоего источника. Необходимо вычислить и отобразить на карте координаты источника
Если вам интересно, как это сделать, добро пожаловать под кат.
Часть 1. Теория и немного геометрии
Пусть, A(xa,ya), B(xb, yb), C(xc, yc) — детекторы сигнала с заданными координатами в некой прямоугольной системе координат. O(xo, yo) — источник сигнала.
Вспоминаем из школьного учебника физики, что амплитуда сигнала обратно пропорциональна квадрату расстояния до источника. Таким образом, расстояние Ra от источника O до детектора A будет равно
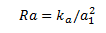
, где ka это некоторый коэффициент, который мы можем получить при калибровке устройств.
Формула для расчета расстояния a1 берем из школьного курса геометрии (стыдно ее тут приводить, но пусть будет для полноты).
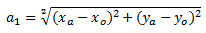
Гетерогенностью среды пренебрегаем. Да, это даст некоторую погрешность, но решение этой проблемы выходит за рамки задачи. Будем считать, что постоянные факторы, влияющие на распространение сигнала (наличие и материал стен, к примеру) — уже заложены в коэффициент ka. Факторы временные — интерференция, переотражение сигнала и т.п. — будут влиять на результат, но на практике даже в помещении мешают не очень сильно.
Таким образом, у нас есть формулы зависимости для расстояния от всех источников.
Если решать задачу «в лоб» — у нас есть система квадратных уравнений, решение которой даст нам точку с координатами xo, yo. Проблема в том, что университетский курс линейной алгебры я слегка подзабыл. После недели размышлений я наткнулся вот на такой способ.
Давайте нарисуем вокруг каждого детектора окружность, радиус которой обратно пропорционален уровню сигнала. Область пересечения всех окружностей и будет содержать источник сигнала. Для простоты – можно считать, что источник находится в центре этой области.
Строим чертеж для случая с тремя детекторами и одним источником.

Здесь B и A ближе всего к источнику сигнала, поэтому диаметр окружности меньше. C дальше всех, диаметр больше. Зависимость диаметра окружности от уровня сигнала определяется экспериментально. Данный чертеж построен в реальных координатах (допустим, метры), для того, чтобы перейти к практике, переведем их в пиксели самым обычным образом. Нужно лишь знать размеры карты (ширина, высота) в пикселях и в метрах. Нелинейностью проекции (если это спутниковый снимок) как и прежде – пренебрегаем. Лучше использовать масштабную схему, в моем проекте это был план помещения.
Часть 2. Переходим к практике
Итак, простое решение найдено, попробуем его воплотить на практике. Серверная часть моего проекта разработана на Java, принимает данные от детекторов по TCP с SSL шифрованием в json формате. Эта часть кода независима, выполняется в отдельном потоке. Полученные события хранятся в базе mysql.
Триангуляция работает в своем потоке, выбирает еще не обработанные события из mysql базы (не позже, чем за 3 секунды до текущего времени – чтобы успеть получить сведения об этом же сигнале от всех источников).
Хотя решение получилось простым и не требует никакой математики, обсчитать пересечение окружностей тоже как-то надо. К счастью, в Java есть библиотека AWT, которая все за нас сделает. Отсутствие оконного интерфейса ее не смущает и отдельные ее классы прекрасно работают на сервере в backend-е.
Привожу немного упрощенный код из проекта.
public static TriangulationPoint triangulate(AlertDbo sourceAlert, AlertDbo[] children, MapFileDbo map) {
…
double ppx = map.getWidth() / map.getRealWidth(); //pixels per feet horizontal
double ppy = map.getHeight() / map.getRealHeight(); //pixels per feet vertical
Итак, ppx/ppy как вы поняли – это коэффициенты для перевода реальных координат в пиксели.
Берем уровень сигнала для первого детектора, вычисляем дистанцию до источника, строим окружность по известным нам координатам с полученным радиусом.
double strength = sourceAlert.getSignalStrength();
double distance = calculateDistance(strength *sourceAlert.getDetector().getKoef());
MapCoordDbo coord = sourceAlert.getCoords();
…
Area area = new Area(new Ellipse2D.Double(coord.getX(), coord.getY(), distance*2, distance*2));
Теперь проходим по всем оставшимся источникам и делаем то же самое. Пересекаем первую окружность с получившейся, результат используем в цикле для оставшихся детекторов. Дополнительный трюк – пересекаем с прямоугольником помещения, иначе может так получиться, что результат выйдет за его пределы, что нам не нужно.
for(int j=0;j<children.length;j++) {
…
strength = children[j].getSignalStrength();
distance = calculateDistance(strength * children[j].getDetector().getKoef());
coord = children[j].getCoords();
area.intersect(new Area(
new Ellipse2D.Double(coord.getX(), coord.getY(), distance*2, distance*2)
));
area.intersect(new Area(new Rectangle(0, 0, map.getWidth(), map.getHeight())));
}
Ну и в конце концов проверяем, что у нас хоть что-то осталось в результате, плюс посчитаем погрешность вычисления (как половина диагонали прямоугольника, в который вписана полученная область).
if(area.getBounds().getWidth()>0 && area.getBounds().getHeight()>0) {
TriangulationPoint tp = new TriangulationPoint();
tp.x = area.getBounds().getCenterX();
tp.y = area.getBounds().getCenterY();
double dx = area.getBounds().getWidth() / 2;
double dy = area.getBounds().getHeight() / 2;
tp.err = Math.sqrt(dx*dx + dy*dy) /2;
return tp;
}
return null;
}
Это функция вычисления расстояния.
public static double calculateDistance(double db) {
double[] dbs = {…};
double[] fts = {…};
double koef = -…;
double prevDb = 70;
double prevDist = 0;
for(int i=0;i<dbs.length;i++) {
if(dbs[i]<db) {
break;
}
koef = (dbs[i] - prevDb) / (fts[i] - prevDist);
prevDb = dbs[i];
prevDist = fts[i];
}
return prevDist + koef * (db - prevDb);
}
Раньше это была логарифмическая функция, но, к сожалению, затухание реального сигнала отличается, пришлось в лаборатории посмотреть на уровень сигнала в нескольких точках и записать значения уровня сигнала и соответствующего расстояния в два массива.
Реальные цифры я на всякий случай убрал, чтобы не нарушить NDA.
Кстати, абсолютно такое же решение возможно на C#. Вместо Area нужно использовать GraphicsPath, там есть метод Intersect. Единственная сложность – поиск центра полученного пересечения. Вот код для поиска центра региона на C#:
private PointF RegionCentroid(Region region, Matrix transform) {
float mx = 0;
float my = 0;
float total_weight = 0;
foreach (RectangleF rect in region.GetRegionScans(transform)) {
float rect_weight = rect.Width * rect.Height;
mx += rect_weight * (rect.Left + rect.Width / 2f);
my += rect_weight * (rect.Top + rect.Height / 2f);
total_weight += rect_weight;
}
return new PointF(mx / total_weight, my / total_weight);
}
Вот так, не обладая достаточными познаниями в математике и физике, с определенными допущениями, можно решить довольно сложную задачу.
Спасибо за внимание!