Вводная
Тем из нас, кому приходится тратить полчаса-час на путешествие из Москвы в Москву, приходится искать, чем занять и разогреть ещё не до конца проснувшийся мозг. Кто-то читает, кто-то кидает птичек, кто-то решает математические головоломки. Например, классическая задачка: среди шести цифр автобусного билета расставить скобки и операторы так, чтобы получилось число 100. Бывает так, что ну никак не удаётся найти решение, и конкретная задачка не отпускает весь оставшийся день. Поневоле задумаешься над алгоритмом.
Решение «в лоб» подстановкой скобок и операторов и проверка на каком-нибудь математическом движке не устраивало, генетические алгоритмы,
Переходим к сути
Очевидно, что сложность алгоритма экспоненциальная: добавляя один лист, мы условно заменяем каждый лист предыдущего дерева на узел. Часть деревьев получаются одинаковыми, но асимптотически разница невелика.
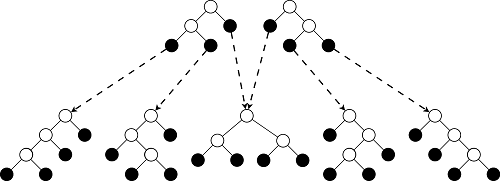
Тем не менее, для шести цифр программа выполняется меньше, чем за секунду, имея таким образом право на жизнь.
Реализовывать будем на C++. Disclaimer: я ещё только учусь. Если вы видите откровенно плохой или просто неоптимальный код — сообщите, пожалуйста.
Пропуская достаточно тривиальный конструктор, рассмотрим создание следующего дерева. В узлах деревьев располагаются операторы, избавляя нас тем самым от возни со скобками и приоритетами. Операторов всего пять: конкатенация, сложение, вычитание, умножение и деление. Унарный минус не используем. Деревья перебираем по следующему принципу: для каждого правого поддерева делаем проход по всем левым поддеревьям. Повторяем для каждого оператора, то есть, пять раз. Внутри поддеревьев происходит ровным счётом то же самое.
Генерация дерева
void BinTree::buildNext()
{
if (type == NUMBER) // Просто лист,
throw BinTreeLastTree(); // сделать с ним ничего нельзя.
try
{
left->buildNext();
}
catch (BinTreeLastTree)
{
try
{
right->buildNext();
}
catch (BinTreeLastTree)
{
bool isLast = false;
leftSize++;
if (leftSize == size)
{
leftSize = 1;
type = (Operation)(type + 1);
if (type == NUMBER) // Если дошли до конца списка операций,
{
type = CONCAT; // то возвращаемся в начало
isLast = true; // и ставим «зарубку».
}
}
delete left;
delete right;
generateSubTrees();
if (isLast)
throw BinTreeLastTree(); // Исключения используем в качестве сигналов о том, что дерево совершило «полный круг».
}
}
}
За вычислением дело тоже не постоит, так что подробно останавливаться на нём не будем.
Главной проблемой были одинаковые решения: кремниевый друг уверял меня, что (1+(2+3)) и ((1+2)+3) — разные вещи. Чтобы объяснить ему обратное, применим «умную» расстановку скобок, а чтобы не тратить время на фильтрацию результата, препоручим это std::set.
Код расстановки скобок
std::string BinTree::toString(bool parentheses)
{
switch (type)
{
case CONCAT:
return left->toString() + right->toString();
case ADD:
{
std::string leftStr = left->toString(!(left->getType() == ADD || left->getType() == SUB)),
rightStr = right->toString(!(right->getType() == ADD || right->getType() == SUB));
return (parentheses?"(":"") + leftStr + operationSymbol[type] + rightStr + (parentheses?")":"");
}
case SUB:
{
std::string leftStr = left->toString(!(left->getType() == ADD || left->getType() == SUB));
return (parentheses?"(":"") + leftStr + operationSymbol[type] + right->toString() + (parentheses?")":"");
}
case MUL:
{
std::string leftStr = left->toString(!(left->getType() == MUL || left->getType() == DIV)),
rightStr = right->toString(!(right->getType() == MUL || right->getType() == DIV));
return (parentheses?"(":"") + leftStr + operationSymbol[type] + rightStr + (parentheses?")":"");
}
case DIV:
return (parentheses?"(":"") + left->toString() + operationSymbol[type] + right->toString() + (parentheses?")":"");
case NUMBER:
{
char str[2] = {(char)(digit[0]+'0'), '\0'};
return str;
}
default:
;
}
throw BinTreeException();
}
Вуаля!
Код вызова
int main()
{
std::string input;
std::cin >> input;
std::cout << busPuzzleSolve(input);
return 0;
}
std::string busPuzzleSolve(std::string input)
{
return BinTree(input.c_str()).solve();
}
Результат
123654
((((1*2)+3)*6)-5)*4
((1*(2+(3*6)))+5)*4
((1*(2+3)*6)-5)*4
((1*(2-3))+6)*5*4
((1*2)+(3*6)+5)*4
((1*2)-(3-6))*5*4
((1*2)-3+6)*5*4
((1/(2-3))+6)*5*4
((12*3)-(6+5))*4
((12*3)-6-5)*4
(1+23+6-5)*4
(1-((2*3)-(6*5)))*4
(1-(2*3)+(6*5))*4
(12+(3*6)-5)*4
1*(((2+3)*6)-5)*4
1*(2+(3*6)+5)*4
1*(2-(3-6))*5*4
1*(2-3+6)*5*4
1+((2+3+6)*(5+4))
Код на SkyDrive в архиве rar (+ файл проекта Code::Blocks) (~2.56 KiB).
Код на pastebin.