Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.
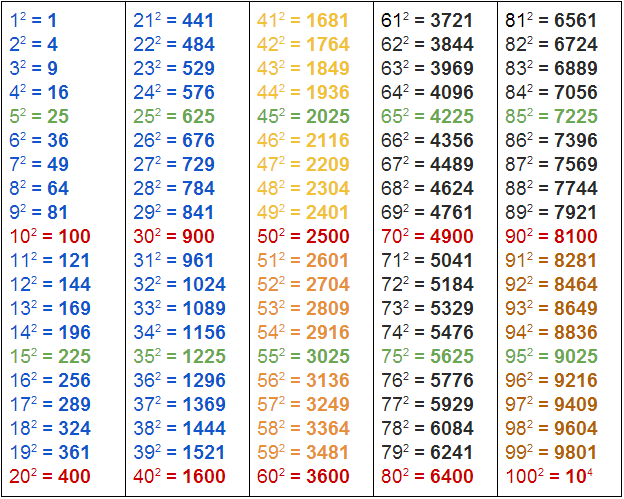
*квадраты до сотни
Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.
Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.
В таблице отмечены красным.
Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.
В таблице отмечены зеленым.
Для чисел от 40 до 50.
Достаточно трудно, верно? Давайте разберем пример:
В таблице отмечены светло-оранжевым.
Для чисел от 50 до 60.
Тоже достаточно трудно для восприятия. Давайте разберем пример:
В таблице отмечены темно-оранжевым.
Для чисел от 90 до 100.
Похоже на правило 3, но с другими коэффициентами. Давайте разберем пример:
В таблице отмечены темно-темно-оранжевым.
Необходимо запомнить квадраты чисел до 40. Звучит дико и трудно, но на самом деле до 20 большинство людей знают квадраты. 25, 30, 35 и 40 поддаются формулам. И остается лишь 16 пар чисел. Их уже можно запомнить при помощи мнемоники (о которой я также хочу рассказать позднее) или любыми другими способами. Как таблицу умножения :)
В таблице отмечены синим.
Вы можете запомнить все правила, а можете запомнить выборочно, в любом случае все числа от 1 до 100 подчиняются двум формулам. Правила же помогут, не используя эти формулы, быстрее посчитать больше 70% вариантов. Вот эти две формулы:
Для чисел от 25 до 50
Например:
Для чисел от 50 до 100
Например:
Конечно не стоит забывать про обычную формулу разложения квадрата суммы (частный случай бинома Ньютона):
UPDATE
Произведения чисел, близких к 100, и, в частности, их квадраты, также можно вычислять по принципу «недостатков до 100»:
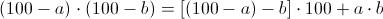
Словами: из первого числа вычитаем «недостаток» второго до сотни и приписываем двузначное произведение «недостатков».
Для квадратов, соответственно, еще проще.
(от sielover)
Возведение в квадрат, возможно, не самая полезная в хозяйстве вещь. Не сразу вспомнишь случай, когда может понадобиться квадрат числа. Но умение быстро оперировать числами, применять подходящие правила под каждое из чисел отлично развивает память и «вычислительные способности» вашего мозга.
Кстати, думаю, все читатели хабры знают, что 64^2 = 4096, а 32^2 = 1024.
Многие квадраты чисел запоминаются на ассоциативном уровне. Например, я легко запомнил 88^2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.
Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.
Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.

*квадраты до сотни
Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.
Правило 1 (отсекает 10 чисел)
Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.
70 * 70 = 4900.
В таблице отмечены красным.
Правило 2 (отсекает 10 чисел)
Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.
75 * 75 = 7 * 8 = 56 … 25 = 5625.
В таблице отмечены зеленым.
Правило 3 (отсекает 8 чисел)
Для чисел от 40 до 50.
XX * XX = 1500 + 100 * вторую цифру + (10 - вторая цифра)^2
Достаточно трудно, верно? Давайте разберем пример:
43 * 43 = 1500 + 100 * 3 + (10 - 3)^2 = 1500 + 300 + 49 = 1849.
В таблице отмечены светло-оранжевым.
Правило 4 (отсекает 8 чисел)
Для чисел от 50 до 60.
XX * XX = 2500 + 100 * вторую цифру + (вторая цифра)^2
Тоже достаточно трудно для восприятия. Давайте разберем пример:
53 * 53 = 2500 + 100 * 3 + 3^2 = 2500 + 300 + 9 = 2809.
В таблице отмечены темно-оранжевым.
Правило 5 (отсекает 8 чисел)
Для чисел от 90 до 100.
XX * XX = 8000+ 200 * вторую цифру + (10 - вторая цифра)^2
Похоже на правило 3, но с другими коэффициентами. Давайте разберем пример:
93 * 93 = 8000 + 200 * 3 + (10 - 3)^2 = 8000 + 600 + 49 = 8649.
В таблице отмечены темно-темно-оранжевым.
Правило №6 (отсекает 32 числа)
Необходимо запомнить квадраты чисел до 40. Звучит дико и трудно, но на самом деле до 20 большинство людей знают квадраты. 25, 30, 35 и 40 поддаются формулам. И остается лишь 16 пар чисел. Их уже можно запомнить при помощи мнемоники (о которой я также хочу рассказать позднее) или любыми другими способами. Как таблицу умножения :)
В таблице отмечены синим.
Вы можете запомнить все правила, а можете запомнить выборочно, в любом случае все числа от 1 до 100 подчиняются двум формулам. Правила же помогут, не используя эти формулы, быстрее посчитать больше 70% вариантов. Вот эти две формулы:
Формулы (осталось 24 числа)
Для чисел от 25 до 50
XX * XX = 100(XX - 25) + (50 - XX)^2
Например:
37 * 37 = 100(37 - 25) + (50 - 37)^2 = 1200 + 169 = 1369
Для чисел от 50 до 100
XX * XX = 200(XX - 50) + (100 - XX)^2
Например:
67 * 67 = 200(67 - 50) + (100 - 67)^2 = 3400 + 1089 = 4489
Конечно не стоит забывать про обычную формулу разложения квадрата суммы (частный случай бинома Ньютона):
(a+b)^2 = a^2 + 2ab + b^2.
56^2 = 50^2 + 2*50*6 + 6*2 = 2500 + 600 + 36 = 3136.
UPDATE
Произведения чисел, близких к 100, и, в частности, их квадраты, также можно вычислять по принципу «недостатков до 100»:
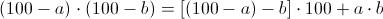
Словами: из первого числа вычитаем «недостаток» второго до сотни и приписываем двузначное произведение «недостатков».
Для квадратов, соответственно, еще проще.
92*92 = (92-8)*100+8*8 = 8464
(от sielover)
Возведение в квадрат, возможно, не самая полезная в хозяйстве вещь. Не сразу вспомнишь случай, когда может понадобиться квадрат числа. Но умение быстро оперировать числами, применять подходящие правила под каждое из чисел отлично развивает память и «вычислительные способности» вашего мозга.
Кстати, думаю, все читатели хабры знают, что 64^2 = 4096, а 32^2 = 1024.
Многие квадраты чисел запоминаются на ассоциативном уровне. Например, я легко запомнил 88^2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.
Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.
Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.