 Доброго времени суток, уважаемые! Так случилось, что вопросом программирования более-менее адекватного ИИ для игры «морской бой» я озадачился где-то в конце 2004 года. Быть может я, не имея должных руководств под рукой, изобретал тогда велосипед, но и в последствии, мне попадались потрясающие своей честностью алгоритмы: стрелять наобум, время от времени подглядывая у игрока расположение кораблей, для выравнивания баланса. В последствии я несколько раз улучшал алгоритм. По последним статьям на Хабре можно судить, что тема актуальна, к тому же — мне есть что добавить к написанному другими пользователями.
Доброго времени суток, уважаемые! Так случилось, что вопросом программирования более-менее адекватного ИИ для игры «морской бой» я озадачился где-то в конце 2004 года. Быть может я, не имея должных руководств под рукой, изобретал тогда велосипед, но и в последствии, мне попадались потрясающие своей честностью алгоритмы: стрелять наобум, время от времени подглядывая у игрока расположение кораблей, для выравнивания баланса. В последствии я несколько раз улучшал алгоритм. По последним статьям на Хабре можно судить, что тема актуальна, к тому же — мне есть что добавить к написанному другими пользователями.Итак, цель моей заметки: реализация
Введение
Я позволю себе сократить вводную часть — для целостности картины рекомендую обратиться к предшествующим статьям:
- Оптимальный алгоритм игры в морской бой (GORKOFF)
- Теория и практика игры «Морской бой» — по-честному (born2fly)
Сразу прошу прощения за некоторые жаргонизмы, вызванные желанием не усложнять повествование громоздкими оборотами, типа «клетка, принадлежащая корпусу корабля», вместо «палуба» (в моём детстве мы называли корабли «четырёхпалубными», «однопалубными» и т.д. — уж не знаю почему).
Отмечу, что корабли могут иметь произвольную форму, но каждая клетка, принадлежащая корпусу («палуба») должна соединяться с остальными по горизонтали и/или вертикали и/или диагонали.
Координатная сетка (на рисунках с визуализацией игрового поля): слева направо – цифры, сверху вниз — буквы.
Примечание
В статье не рассмотрена оптимизация на уровне кода, а алгоритмы приведены в максимально развёрнутом (подробном) виде.
Помимо поясняющих рисунков, статья содержит скриншоты из моих программ/игр.
Режимы
В стратегии ведения боя явно можно выделить две стадии (два режима).
- "Разведка боем". На карте противника нет ни одного «раненого» корабля. ИИ выбирает точку для атаки «полностью здорового» судна.
- "Добивание". На карте есть клетка (клетки) отмеченные как «ранил». ИИ пытается определить корпус и ориентацию судна, чтобы потопить его.
Большинство людей, «ранив» вражеский корабль, пытается затопить именно его. Это логично, так как потопление сделает бессмысленной для стрельбы дополнительную (буферную) зону вокруг затонувшего корабля, увеличив количество информации о вражеском поле и снизив вероятность выстрелить мимо. К тому же, гарантировано, что следующая точка, занимаемая кораблём, будет вычислена, самое худшее, в 4 (при диагональных кораблях — в 8) ходов, в то время как попытка подбить новое судно может быть куда как менее продуктивна.
Таким образом, ИИ начинает работу в режиме «Разведка», в случае некритического повреждения («ранил») вражеского судна переходит в режим «Добивание». Во втором режиме ИИ функционирует пока корабль не будет уничтожен, после чего снова выбирается первый режим.
При оптимизации алгоритма под «классическую» эскадру (с кораблями без изгибов), может быть удобно выделить третий режим (об этом ниже). Первый и второй режим отличаются особенностями формирования матрицы вероятностей (об этом ниже), и логикой смены режима.
Разведка
 Для того, чтобы добиться уровня абстракции, позволяющего атаковать эскадру, сформированную из произвольного количества судов произвольной формы (тем не менее, согласно правилам, данная информация о сопернике заранее известна), введём понятие вероятности нахождения в данной клетке игрового поля фрагмента неподбитого корабля («палубы»). Критерием для выбора точки атаки будет величина, пропорциональная упомянутой выше вероятности, а именно: нормированное количество палуб, которые могут попасть в эту клетку, если каждый из кораблей противника (из тех, что на плаву) попытаться разместить на поле всеми возможными способами.
Для того, чтобы добиться уровня абстракции, позволяющего атаковать эскадру, сформированную из произвольного количества судов произвольной формы (тем не менее, согласно правилам, данная информация о сопернике заранее известна), введём понятие вероятности нахождения в данной клетке игрового поля фрагмента неподбитого корабля («палубы»). Критерием для выбора точки атаки будет величина, пропорциональная упомянутой выше вероятности, а именно: нормированное количество палуб, которые могут попасть в эту клетку, если каждый из кораблей противника (из тех, что на плаву) попытаться разместить на поле всеми возможными способами.Поясню: берём матрицу (далее — «P-матрица»), размерами соответствующую, размерам поля противника. Заполняем её нулями. Берём первый доступный (то есть ещё не утонувший) корабль противника из списка кораблей соперника и пробуем его разместить (в соответствии с правилами и опираясь на полученную в ходе обстрела информацию) в координатах А1. Если разместить удалось, то инкрементируем в P-матрице все элементы (соответствующие клеткам игрового поля), накрываемые корпусом корабля. Повторяем процедуру для всех координат. Затем поворачиваем корабль на 90 градусов и ещё раз повторяем проход для всех координат. То же повторяем для 180 и 270 градусов.
В итоге, мы заполним P-матрицу значениями, которые для удобства нормируем по максимуму. Полученная характеристика принимает единичное значение в наиболее вероятных точках нахождения кораблей и нулевое в невозможных. Например, на необстрелянной карте, центральные точки (для классической эскадры) имеют максимальное значение.
Стоит определиться с термином "вероятность", чтобы избежать его превратного толкования. Данный алгоритм предполагает равномерное расположение кораблей по полю. Попытки распихать суда по краям поля должны детектироваться отдельно. Например, можно ввести весовую матрицу, которая каким-то образом будет формироваться в ходе обучения (предшествующих игр с данным соперником): если до этого противник никогда не ставил корабль в центре поля, то соответствующие клетки весовой матрицы будут иметь минимальный коэффициент. В любом случае: это не шахматы — всегда есть неизвестная информация, которая, при удачном стечении обстоятельств, может дать преимущество «обороняющемуся».
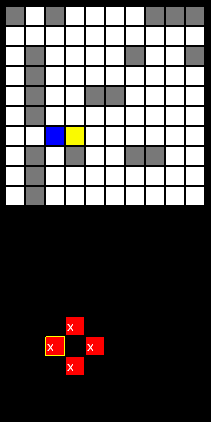
 На рисунке слева приведена визуализация P-матрицы при первом ходе ИИ в игре с классической эскадрой. Цвет [ RGB(0;0;0); RGB(255;0;0) ] показывает значение клетки. Белым крестиком отмечены максимумы значений. Как нетрудно заметить, максимумов, как правило, несколько. Чтобы разнообразить игру и исключить потенциальную возможность предугадать точку атаки, выбранную ИИ (и соответствующим образом расставить корабли), выбирать будем произвольную точку из максимумов (на рисунке — имеет жёлтую рамку).
На рисунке слева приведена визуализация P-матрицы при первом ходе ИИ в игре с классической эскадрой. Цвет [ RGB(0;0;0); RGB(255;0;0) ] показывает значение клетки. Белым крестиком отмечены максимумы значений. Как нетрудно заметить, максимумов, как правило, несколько. Чтобы разнообразить игру и исключить потенциальную возможность предугадать точку атаки, выбранную ИИ (и соответствующим образом расставить корабли), выбирать будем произвольную точку из максимумов (на рисунке — имеет жёлтую рамку).Ответы соперника «мимо» или «убил» оставляют режим работы ИИ без изменений (во втором случае необходимо произвести ряд действий). Ответы запоминаются в специальную матрицу, аккумулирующую знания о расстановке сил противника. Именно "на этой матрице" производятся попытки размещения кораблей при вычислении P-матрицы.
При использовании только классической эскадры возможно провести оптимизацию вычисления матрицы (об этом ниже).
Добивание
После того, как от соперника получен ответ «ранил», ИИ переходит во второй режим функционирования.
 В этом режиме при вычислении P-матрицы количество «палуб» проверяемого корабля должно быть больше, чем количество клеток «ранил». Корабль инкрементирует значения элементов P-матрицы, только если данное его размещение накрывает все клетки, отмеченные как «ранил». После перебора всех кораблей происходит дополнительное акцентирование на клетках «ранил». Так как стрелять в такие клетки бессмысленно (но, в отличии от клеток «мимо», они являются частью корабля, и потому имеют ненулевое значение в P-матрице), значения соответствующих элементов P-матрицы обнуляются. Обнуляются так же клетки, не примыкающие ни к одной из клеток «ранил». Последнее обстоятельство связано с тем, что при некотором стечении обстоятельств, усиленном экзотической формой кораблей не классической эскадры, можно выбрать в P-матрице максимум, который соответствует другом кораблю (что возможно, только если атакуемая клетка отстоит от «раненой»). Такая ситуация приведёт к тому, что ИИ будет пытаться подобрать корабль, удовлетворяющий обеим клеткам, что рано или поздно кончится неудачей. Это в свою очередь приведёт к тому, что все элементы P-матрицы примут нулевые значения, а, следовательно, уже обстрелянные точки станут адекватными вариантами атаки. Поэтому, разумной является атака близлежащих точек.
В этом режиме при вычислении P-матрицы количество «палуб» проверяемого корабля должно быть больше, чем количество клеток «ранил». Корабль инкрементирует значения элементов P-матрицы, только если данное его размещение накрывает все клетки, отмеченные как «ранил». После перебора всех кораблей происходит дополнительное акцентирование на клетках «ранил». Так как стрелять в такие клетки бессмысленно (но, в отличии от клеток «мимо», они являются частью корабля, и потому имеют ненулевое значение в P-матрице), значения соответствующих элементов P-матрицы обнуляются. Обнуляются так же клетки, не примыкающие ни к одной из клеток «ранил». Последнее обстоятельство связано с тем, что при некотором стечении обстоятельств, усиленном экзотической формой кораблей не классической эскадры, можно выбрать в P-матрице максимум, который соответствует другом кораблю (что возможно, только если атакуемая клетка отстоит от «раненой»). Такая ситуация приведёт к тому, что ИИ будет пытаться подобрать корабль, удовлетворяющий обеим клеткам, что рано или поздно кончится неудачей. Это в свою очередь приведёт к тому, что все элементы P-матрицы примут нулевые значения, а, следовательно, уже обстрелянные точки станут адекватными вариантами атаки. Поэтому, разумной является атака близлежащих точек.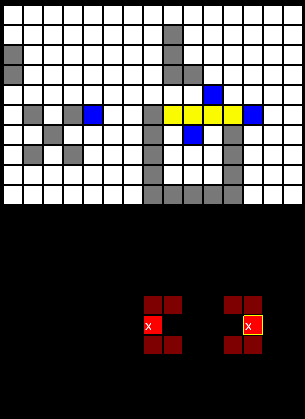 На рисунке слева представлены две матрицы (точнее, визуализации их значений). Верхняя — с расположенными на белом поле серыми кораблями. На предыдущем ходу ИИ осуществил успешную атаку на Ж4 (то обстоятельство, что первый же ход увенчался успехом — совпадение), «раненая» клетка отмечена жёлтым. Внизу приведена P-матрица. Учитывая геометрию актуального набора кораблей, у ИИ было 4 равновероятных варианта атаки (отмеченные крестиком клетки), из которых он выбрал Ж3 (клетка с жёлтой рамкой). Ход завершился промахом (синяя клетка в верхней матрице).
На рисунке слева представлены две матрицы (точнее, визуализации их значений). Верхняя — с расположенными на белом поле серыми кораблями. На предыдущем ходу ИИ осуществил успешную атаку на Ж4 (то обстоятельство, что первый же ход увенчался успехом — совпадение), «раненая» клетка отмечена жёлтым. Внизу приведена P-матрица. Учитывая геометрию актуального набора кораблей, у ИИ было 4 равновероятных варианта атаки (отмеченные крестиком клетки), из которых он выбрал Ж3 (клетка с жёлтой рамкой). Ход завершился промахом (синяя клетка в верхней матрице).При наборах кораблей с экзотической геометрией, матрицы могут выглядеть куда как более загадочно. Хоть я и привык играть с классической эскадрой, но не вижу ничего предосудительного в использовании кораблей почти произвольной формы. Такие модели, могут имитировать, например, скоростной катамаран, RV FLIP, тяжёлый авианесущий крейсер, «бетонный линкор». Не говоря уже о том, что неподвижные (по логике игры) объекты можно интерпретировать и как маломобильные (или стационарные) стратегические объекты на суше во время глобальной войны. С позиции игрового процесса, на мой взгляд, подобное усложнение лишь добавляет азарта при игре.
На рисунке справа показана ситуация: после нескольких удачных залпов ИИ выбирает не то направление и промахивается на Е13. Обратите внимание, что было 10 вариантов хода, имеющих смысл, из них 2 наиболее вероятных.
Режим «добивание» переключается на «разведку» только после ответа соперника «убил». Как и при первом режиме, полученная в ходе обстрела информация учитывается при формировании P-матрицы на следующем ходу.
Классика
Использование классической эскадры, то есть «одномерных» кораблей, позволяет конкретизировать подход, сократив число операций. С одной стороны, нижеописанные алгоритмы менее гибки и экономят крохи производительности (учитывая, актуальный уровень техники, и большой, обусловленный жанром, запас времени на ход), но с другой стороны — эти алгоритмы более близки к человеческому восприятию игры, что может облегчить понимание процесса функционирования ИИ.
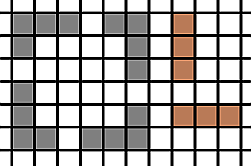 Отмечу, что специфика геометрии классических кораблей (а именно — одномерность), делает вероятность разместить корпус, развёрнутый на 180 градусов (в зависимости от точки вращения — с соответствующей коррекцией координат) равной вероятности размещения корпуса с нулевым углом вращения. Иными словами, для всех кораблей невозможно определить: расположен он сверху вниз или снизу вверх, слева направо или справа налево (смотри рисунок слева: 4 угла вращения для серого корпуса и 2 — для классического коричневого). Это обстоятельство позволяет уменьшить количество вычислений, оставив для всех кораблей лишь тест на размещение при угле 0 и 90 градусов.
Отмечу, что специфика геометрии классических кораблей (а именно — одномерность), делает вероятность разместить корпус, развёрнутый на 180 градусов (в зависимости от точки вращения — с соответствующей коррекцией координат) равной вероятности размещения корпуса с нулевым углом вращения. Иными словами, для всех кораблей невозможно определить: расположен он сверху вниз или снизу вверх, слева направо или справа налево (смотри рисунок слева: 4 угла вращения для серого корпуса и 2 — для классического коричневого). Это обстоятельство позволяет уменьшить количество вычислений, оставив для всех кораблей лишь тест на размещение при угле 0 и 90 градусов. Одномерность же позволяет определить и количество попадающих в клетку «палуб», опираясь лишь на длину корабля и расстояния до препятствий. На рисунке справа: красным отмечены клетки-препятствия (например, буферные зоны других кораблей), зелёным кружком — клетка, для которой вычисляется характеристика. Производится попытка разместить корабль длиной в три клетки. Нетрудно прикинуть, что результаты (сверху вниз) будут следующие: 0, 0, 1, 1. Очевидно, что в первых двух случаях, расстояния между препятствиями принципиально не хватает на корпус требуемой длины. В четвёртом случае становится ясно, что увеличить количество возможных положений корабля, можно только отодвигая противоположную границу.
Одномерность же позволяет определить и количество попадающих в клетку «палуб», опираясь лишь на длину корабля и расстояния до препятствий. На рисунке справа: красным отмечены клетки-препятствия (например, буферные зоны других кораблей), зелёным кружком — клетка, для которой вычисляется характеристика. Производится попытка разместить корабль длиной в три клетки. Нетрудно прикинуть, что результаты (сверху вниз) будут следующие: 0, 0, 1, 1. Очевидно, что в первых двух случаях, расстояния между препятствиями принципиально не хватает на корпус требуемой длины. В четвёртом случае становится ясно, что увеличить количество возможных положений корабля, можно только отодвигая противоположную границу.Начинаем двигать препятствие слева, и получаем характеристики: 1, 2, 3, 3. Из результатов видно, что характеристика ограничена сверху длиной корабля.
Резюмируя:
- Если сумма расстояний + 1 (тестируемая клетка) меньше, чем длина корабля, то результат равен 0.
- Если сумма расстояний + 1 равна длине корабля, то результат равен 1.
- В остальных случаях, характеристика:
- не меньше 1
- не превышает длину корабля
- ограничивается минимальным расстоянием до препятствия
Исходя из вышесказанного, код функции, вычисляющей характеристику имеет вид:
inline unsigned minimum(unsigned A,unsigned B){
return A<B?A:B;
}
unsigned Bf(unsigned A,unsigned B,unsigned K){
if(A+B+1<K) return 0;
if(A+B+1==K) return 1;
return minimum(minimum(A,B)+1,K);
}
 Если в эскадре противника несколько кораблей одной длины, то, чтобы учесть их суммарное влияние на клетку, достаточно посчитать Bf один раз и умножить результат на количество единиц техники. Перебрав все уникальные длины кораблей противника (для классики — 4 варианта) и учтя количество кораблей с такой длиной корпуса на плаву, получаем некую характеристику Gf. Данная характеристика описывает количество «палуб», попадающих в клетку при фиксированной ориентации (но не координатах) всех кораблей (например, для рисунка выше — горизонтальной). Итоговая характеристика G2df, представляет собой сумму Gf для горизонтальной и вертикальной ориентации. Матрица значений G2df для всех клеток игрового поля, является аналогом P-матрицы, рассмотренной выше. Опираясь на максимумы матрицы, выбираем точку атаки. В случае успеха, переходим в режим добивания, где выбираем клетку, соответствующую наиболее свободному (но в пределах максимальной длины корпуса среди неуничтоженных кораблей противника) направлению. Если несколько направлений равновероятны — выбираем случайным образом. Выбрав направление атаки, продолжаем огонь до одного из исходов:
Если в эскадре противника несколько кораблей одной длины, то, чтобы учесть их суммарное влияние на клетку, достаточно посчитать Bf один раз и умножить результат на количество единиц техники. Перебрав все уникальные длины кораблей противника (для классики — 4 варианта) и учтя количество кораблей с такой длиной корпуса на плаву, получаем некую характеристику Gf. Данная характеристика описывает количество «палуб», попадающих в клетку при фиксированной ориентации (но не координатах) всех кораблей (например, для рисунка выше — горизонтальной). Итоговая характеристика G2df, представляет собой сумму Gf для горизонтальной и вертикальной ориентации. Матрица значений G2df для всех клеток игрового поля, является аналогом P-матрицы, рассмотренной выше. Опираясь на максимумы матрицы, выбираем точку атаки. В случае успеха, переходим в режим добивания, где выбираем клетку, соответствующую наиболее свободному (но в пределах максимальной длины корпуса среди неуничтоженных кораблей противника) направлению. Если несколько направлений равновероятны — выбираем случайным образом. Выбрав направление атаки, продолжаем огонь до одного из исходов:- 1. Корабль уничтожен. Переходим в режим поиска новой жертвы.
- 2. Промах. Значит атака была начата не с крайней точки. Инвертируем направление обстрела, продолжаем атаку от точки первого «ранения»
- 2.1. Промах на первом же выстреле в режиме добивания. Значит, направление выбрано ошибочно. Необходимо заново вычислить вероятности направлений, учитывая полученную информацию.
- 3. Огонь в выбранном направлении не имеет смысла (например, достигнут край игрового поля), а корабль ещё на плаву. Решение аналогично пункту 2.
Заключение
 Итак, теперь вы знаете как вести огонь по противнику, и как оптимально расставить корабли (см. ссылки в начале статьи).
Итак, теперь вы знаете как вести огонь по противнику, и как оптимально расставить корабли (см. ссылки в начале статьи).Самому мне хотелось бы узнать мысли сообщества по поводу неоптимальной (равномерной) расстановки кораблей: даже в классическом варианте возможна тупиковая ситуация, если не двигать уже выставленные корабли. Для кораблей произвольной формы, вероятно, можно обосновать критерий на минимальные размеры поля для размещения.
Спасибо, всем дочитавшим статью до конца. Постараюсь ответить на интересующие вопросы.
Просьба: указания на ошибки и прочие предложения по редактуре пишите в личку, чтобы не разбавлять обсуждение.
Критика
Спасибо за интересные и конструктивные замечания!
mayorovp уточняет, что рассмотренный алгоритм работает оптимально лишь в некотором приближении. В самом деле, рассмотрим предложенную ситуацию:
на поле осталось пять клеток в линии и два корабля 1х2, то оптимальный алгоритм уничтожит их за 4 выстрела без промахов. Ваш же алгоритм определит, что «вероятность» нахождения корабля в центре — максимальна, и может попытаться выстрелить туда (в одном случае из трех).
Действительно:
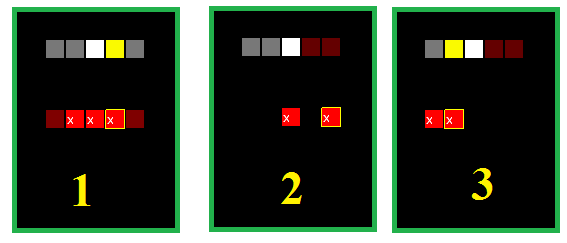
В отличии от очевидной человеку оптимальной тактики, ИИ с вероятностью в 33% предпримет априорно неверное решение, атаковав А3 на N-ом ходу. На (N+1)-ом ходу (в случае успеха на N-ом) может быть реализована ошибочная атака с вероятностью в 50% (на рисунке — атака на А3 на втором слайде).
Как отмечает mayorovp,
Оптимальный алгоритм долженОтмечается и слабость адаптации к неравномерному распределению кораблей на игровом поле в ходе обучения:
1) при подсчете вероятности размещать на поле не один корабль, а всю эскадру противника с учетом ограничений на соседство;
2) учитывать, что противник может намеренно разместить свою эскадру в наименее вероятной позиции (по краям, например), и предпринимать ответные действия уже в первой игре, вместо обучения под конкретного соперника.
MichaelBorisov приводит ссылку на своё исследование «Бот для игры в „Морской бой“: история, теория, практика».
К сожалению, мой «всеобъемлющий» подход столкнулся со сложностями вычислительного характера, что даже на современных компьютерах просчитать все комбинации невозможно, а можно лишь искать некоторое приближение методом Монте-Карло, но и это оказалось затруднительно в реальном времени.
zorge_van_daar поднимает интересный вопрос: возможно ли вместо добивания, переключиться на поиск новых кораблей (принимая во внимание полученную после атаки информацию), так как обнаружить всю технику противника — и есть основная цель игры, а уничтожить обнаруженное можно и после.
По вполне обоснованному совету limon_spb и других пользователей, убрал излишне претенциозную характеристику «оптимальный». Так как подобное заявление требует объективного доказательства, которое в статье не приведено, и, в силу вышесказанного, приведено быть не может.