Как-то раз я решил написать игру. Для себя и в своё удовольствие. Передо мной стоял выбор – использовать всё готовенькое ака Box2D или написать для неё физику самому. Второй вариант показался мне более интересным, и я принялся выискивать в просторах сети информацию, которая помогла бы мне написать всё необходимое. Выискал. Как результат получился очень гибкий(как для игры) и простой физический движок. Основой движка стал метод численного интегрирования Верле.

Метод Верле описывает движение материальных точек во времени. Для этого существуют разные методы. Например, такая система уравнений.
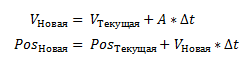
Объединив 2 уравнения, мы получим
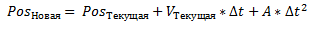
Уравнение Верле мало чем отличается от записи выше.

Как видно, в методе Верле скорость точки выражается через разницу между её текущей и старой координатой. Отлично, нам меньше мороки. Точность вычислений от этого падает, но мы и не атомные реакторы рассчитываем. Плюс это делает расчёт столкновений до смешного простым. Рассмотрим движение точки на примере:

Мы видим, что текущая и старая координаты точки выбраны таким образом, что она неотвратимо движется вправо навстречу с синим квадратом. Заглядывая немного вперёд, скажу, что при обнаружении столкновения с квадратом для обработки этого столкновения достаточно вывести текущую координату точки за пределы квадрата. Всё. Так как скорость тут выражается через разницу координат, изменение текущей или старой координаты автоматически приводит и к изменению скорости движения точки.

Если облечь всё это в код на С++, то получится что-то такое
Этого достаточно для описания движения материальных точек. И это хорошо, если у вас в игре планируются только точки. Если же хочется чего-то более интересного, надо делать твёрдые тела. В природе твёрдое тело это много точек-атомов, соединённых между собой мистическими силами природы. Увы, для симуляции физики в игре подобный метод подходит плохо, ни один компьютер не сможет выдержать расчётов миллиардов и миллиардов точек и связей между ними. Поэтому мы обойдёмся моделированием вершин физических тел. Для квадрата таким образом будет достаточно 4 точек и связей между ними. Осталось только описать эти связи. Очевидно, что расстояние между вершинами должно оставаться постоянным. Если расстояние между вершинами будет меняться, тело будет деформироваться, а мы этого не хотим (те, кто этого хотят, пока молчат). Как же сохранить расстояние между вершинами постоянным? В реальности для решения этой задачи достаточно было бы засунуть между вершинами арматурину соответствующей длинны. Не мудрствуя лукаво, поступим так же и в нашей симуляции. Создадим класс, который будет описывать эту воображаемую арматурину, удерживающую вершины на необходимом расстоянии. Алгоритм, выполняющий эту работу, будет вызываться сразу же после обработки движения точек-вершин. В сути своей он очень простой. Мы расчитываем вектор между двумя вершинами, соединёнными нашей воображаемой арматуриной и сравниваем длину этого вектора с нашей эталонной длинной. Если длины отличаются, нам остаётся только сдвинуть\раздвинуть вершины на необходимое расстояние, что бы длины снова совпадали и вуаля – дело в шляпе.
Вот так это всё выглядит в коде:
Вот так вот. Если создать несколько вершин и соединить их между собой такими вот сторонами, результирующее тело будет демонстрировать свойства твёрдого тела, в том числе вращение, вызываемое столкновением с другими телами и полом. Как это всё работает? Ведь мы всего-то добавили новое правило для сохранения расстояния между точками, а тут на – сразу твёрдое тело. Секрет в том самом методе интегрирования Верле. Как мы помним, этот метод не оперирует скоростями, вместо этого в нём используется разница между координатам текущего и старого положения точки. Как следствие, от изменения координаты изменится и скорость. А для сохранения постоянной длинны между вершинами мы как раз и меняем их координаты. Итоговое изменение скорости вершин даёт эффект, приближённо напоминающий поведение твёрдых тел. Точнее почти твёрдых. В том виде, в котором код находится сейчас, тела будут деформироваться при ударах о пол и друг об друга. Почему? Всё очень просто. Если вершина присоединена более чем к одной стороне, а так обычно и будет происходить, корректировка длины одной из сторон автоматически приведёт к изменению длины другой стороны.
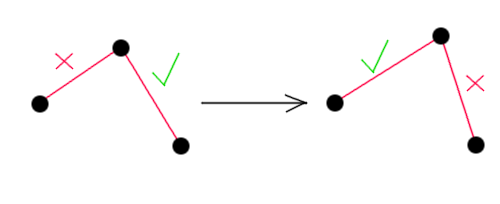
Единственным методом лечения этой болезни является множественный вызов функции, корректирующей длины сторон. Чем больше раз её вызвать, тем точнее будет аппроксимация. Сколько раз это делать зависит только от вашей фантазии. На этом первая часть статьи заканчивается. В следующей части будут рассмотрены такие моменты как обнаружение и обработка столкновений между телами а также некоторые финты ушами, которые можно проделать при помощи этого метода.

Метод Верле описывает движение материальных точек во времени. Для этого существуют разные методы. Например, такая система уравнений.
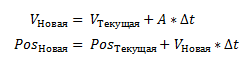
Объединив 2 уравнения, мы получим
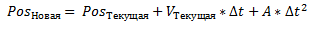
Уравнение Верле мало чем отличается от записи выше.

Как видно, в методе Верле скорость точки выражается через разницу между её текущей и старой координатой. Отлично, нам меньше мороки. Точность вычислений от этого падает, но мы и не атомные реакторы рассчитываем. Плюс это делает расчёт столкновений до смешного простым. Рассмотрим движение точки на примере:

Мы видим, что текущая и старая координаты точки выбраны таким образом, что она неотвратимо движется вправо навстречу с синим квадратом. Заглядывая немного вперёд, скажу, что при обнаружении столкновения с квадратом для обработки этого столкновения достаточно вывести текущую координату точки за пределы квадрата. Всё. Так как скорость тут выражается через разницу координат, изменение текущей или старой координаты автоматически приводит и к изменению скорости движения точки.

Если облечь всё это в код на С++, то получится что-то такое
struct Point
{
Vec2 Position;
Vec2 OldPosition;
Vec2 Acceleration;
};
class Physics
{
int PointCount;
Point* Points[ MAX_VERTICES ];
float Timestep;
public:
void UpdateVerlet();
};
void Physics::UpdateVerlet()
{
for( int I = 0; I < PointCount; I++ )
{
Point& P = *Points[ I ];
Vec2 Temp = P.Position;
P.Position += P.Position - P.OldPosition + P.Acceleration*Timestep*Timestep;
P.OldPosition = Temp;
}
}
Этого достаточно для описания движения материальных точек. И это хорошо, если у вас в игре планируются только точки. Если же хочется чего-то более интересного, надо делать твёрдые тела. В природе твёрдое тело это много точек-атомов, соединённых между собой мистическими силами природы. Увы, для симуляции физики в игре подобный метод подходит плохо, ни один компьютер не сможет выдержать расчётов миллиардов и миллиардов точек и связей между ними. Поэтому мы обойдёмся моделированием вершин физических тел. Для квадрата таким образом будет достаточно 4 точек и связей между ними. Осталось только описать эти связи. Очевидно, что расстояние между вершинами должно оставаться постоянным. Если расстояние между вершинами будет меняться, тело будет деформироваться, а мы этого не хотим (те, кто этого хотят, пока молчат). Как же сохранить расстояние между вершинами постоянным? В реальности для решения этой задачи достаточно было бы засунуть между вершинами арматурину соответствующей длинны. Не мудрствуя лукаво, поступим так же и в нашей симуляции. Создадим класс, который будет описывать эту воображаемую арматурину, удерживающую вершины на необходимом расстоянии. Алгоритм, выполняющий эту работу, будет вызываться сразу же после обработки движения точек-вершин. В сути своей он очень простой. Мы расчитываем вектор между двумя вершинами, соединёнными нашей воображаемой арматуриной и сравниваем длину этого вектора с нашей эталонной длинной. Если длины отличаются, нам остаётся только сдвинуть\раздвинуть вершины на необходимое расстояние, что бы длины снова совпадали и вуаля – дело в шляпе.
Вот так это всё выглядит в коде:
struct Edge
{
Vertex* V1;
Vertex* V2;
float OriginalLength;
};
void Physics::UpdateEdges()
{
for( int I = 0; I < EdgeCount; I++ )
{
Edge& E = *Edges[ I ];
//Расчёт вектора между вершинами
Vec2 V1V2 = E.V2->Position - E.V1->Position;
float V1V2Length = V1V2.Length();
//Расчёт разницы в длине
float Diff = V1V2Length - E.OriginalLength;
V1V2.Normalize();
//Корректировка расстояния
E.V1->Position += V1V2*Diff*0.5f;
E.V2->Position -= V1V2*Diff*0.5f;
}
}
Вот так вот. Если создать несколько вершин и соединить их между собой такими вот сторонами, результирующее тело будет демонстрировать свойства твёрдого тела, в том числе вращение, вызываемое столкновением с другими телами и полом. Как это всё работает? Ведь мы всего-то добавили новое правило для сохранения расстояния между точками, а тут на – сразу твёрдое тело. Секрет в том самом методе интегрирования Верле. Как мы помним, этот метод не оперирует скоростями, вместо этого в нём используется разница между координатам текущего и старого положения точки. Как следствие, от изменения координаты изменится и скорость. А для сохранения постоянной длинны между вершинами мы как раз и меняем их координаты. Итоговое изменение скорости вершин даёт эффект, приближённо напоминающий поведение твёрдых тел. Точнее почти твёрдых. В том виде, в котором код находится сейчас, тела будут деформироваться при ударах о пол и друг об друга. Почему? Всё очень просто. Если вершина присоединена более чем к одной стороне, а так обычно и будет происходить, корректировка длины одной из сторон автоматически приведёт к изменению длины другой стороны.

Единственным методом лечения этой болезни является множественный вызов функции, корректирующей длины сторон. Чем больше раз её вызвать, тем точнее будет аппроксимация. Сколько раз это делать зависит только от вашей фантазии. На этом первая часть статьи заканчивается. В следующей части будут рассмотрены такие моменты как обнаружение и обработка столкновений между телами а также некоторые финты ушами, которые можно проделать при помощи этого метода.