Добрый день, уважаемые читатели.
В сегодняшней статье, я попытаюсь описать процесс анализа временных рядов с помощью python и модуля statsmodels. Данный модуль предоставляет широкий набор средств и методов для проведения статистического анализа и эконометрики. Я попытаюсь показать основные этапы анализа таких рядов, в заключении мы построим модель ARIMA.
Для примера взяты реальные данные по товарообороту одного из складских комплексов Подмосковья.
Для начала загрузим данные и посмотрим на них:
Итак, как можно заметить функция read_csv(), в данном случем помимо указания параметров, которые задают используемые колонки и индекс, можно заметить еще 3 параметра для работы с датой. Остановимся на них поподробнее.
parse_dates задает имена столбцов, которые будут преобразованы в тип DateTime. Стоит отметить, что если в данном столбце будут пустые значения парсинг не удастся и вернется столбец типа object. Чтобы этого избежать надо добавить параметр keep_default_na=False.
Заключительный параметр dayfirst указывает функции парсинга, что первое в строке первым идет день, а не наоборот. Если не задать этот параметр, то функция может не правильно преобразовывать даты и путать месяц и день местами. Например 01.02.2013 будет преобразовано в 02-01-2013, что будет неправильно.
Выделим в отдельную серию временной ряд со значениями отгрузкок:
Итак у нас теперь есть временной ряд и можно перейти к его анализу.
Для начала давайте посмортим график нашего ряда:
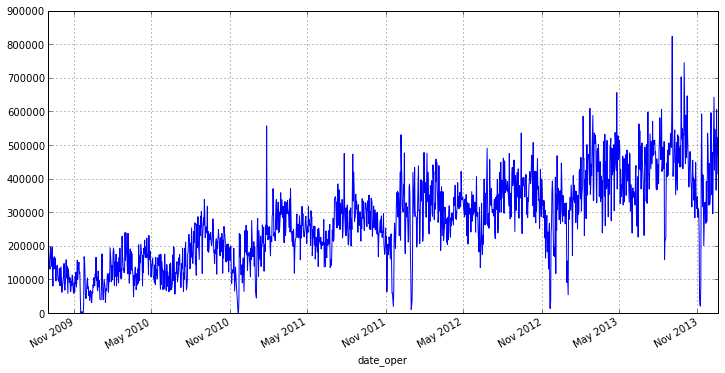
Из графика видно, что наш ряд имеет небольшое кол-во выбросов, которые влияют на разброс. Кроме того анализировать отгрузки за каждый день не совсем верно, т.к., например, в конце или начале недели будут дни в которые товара отгружается значительно больше, нежели в остальные. Поэтому есть смысл перейти к недельному интервалу и среднему значению отгрузок на нем, это избавит нас от выбросов и уменьшит колебания нашего ряда. В pandas для этого есть удобная функция resample(), в качестве параметров ей передается период округления и аггрегатная функция:
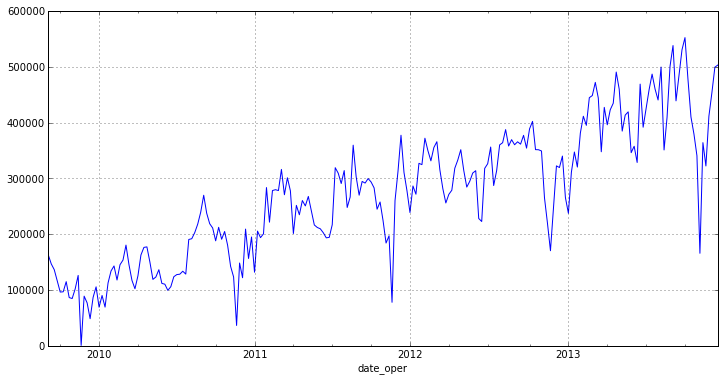
Как можно заметить, новый график не имеет ярких выбросов и имеет ярко выраженный тренд. Из это можно сделать вывод о том, что ряд не является стационарным[1].
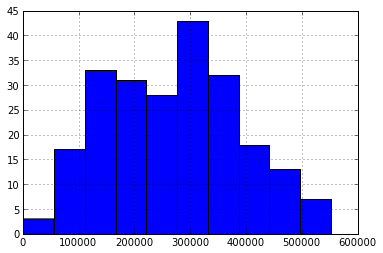
Как можно заметить из характеристик и гистограммы, ряд у нас более менее однородный и имеет относительно небольшой разброс о чем свидетельствует коэффициент вариации: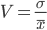 , где
, где 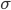 — cреднеквадратическое отклонение,
— cреднеквадратическое отклонение, 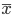 — среднее арифметическое выборки. В нашем случае он равен:
— среднее арифметическое выборки. В нашем случае он равен:
V = 0.437022
Проведем тест Харки — Бера для определения номарльности распределения, чтобы подтвердить предположение об однородности. Для этого в существует функция jarque_bera(), которая возвращает значения данной статистики:
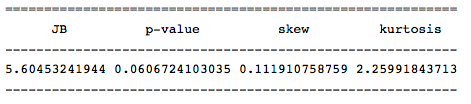
Значение данной статистика свидетельствует о том, нулевая гипотеза о нормальности распределения отвергается с малой вероятностью (probably > 0.05), и, следовательно, наш ряд имеет нормального распределения.
Функция SimpleTable() служит для оформления вывода. В нашем случае на вход ей подается массив значений (размерность не больше 2) и список с названиями столбцов или строк.
Многие методы и модели основаны на предположениях о стационарности ряда, но как было замечено ранее наш ряд таковым скорее всего не является. Поэтому для проверки проверки стационарности давайте проведем обобщенный тест Дикки-Фуллера на наличие единичных корней. Для этого в модуле statsmodels есть функция adfuller():
adf: -1.38835541357
p-value: 0.58784577297
Critical values: {'5%': -2.8753374677799957, '1%': -3.4617274344627398, '10%': -2.5741240890815571}
есть единичные корни, ряд не стационарен
Проведенный тест подтвердил предположения о не стационарности ряда. Во многих случаях взятие разности рядов позволяет это сделать.Если, например, первые разности ряда стационарны, то он называется интегрированным рядом первого порядка.
Итак, давайте определим порядок интегрированного ряда для нашего ряда:
В коде выше функция diff() вычисляет разность исходного ряда с рядом с заданным смещением периода. Период смещения передается как параметр period. Т.к. в разности первое значение получиться неопределенным, то нам надо избавиться от него для этого и используется метод dropna().
Проверим получившийся ряд на стационарность:
adf: -5.95204224907
p-value: 2.13583392404e-07
Critical values: {'5%': -2.8755379867788462, '1%': -3.4621857592784546, '10%': -2.574231080806213}
единичных корней нет, ряд стационарен
Как видно из кода выше получившийся ряд первых разностей приблизился к стационарному. Для полной уверенности разобъем его на несколько промежутков и убедимся мат. ожидания на разных интервалах:
p-value: 0.693072039563
Высокое p-value дает нам возможность утверждать, что нулевая гипотеза о равенстве средних верна, что свидетельствует о стационарности ряда. Осталось убедиться в отсутствии тренда для этого построим график нашего нового ряда:
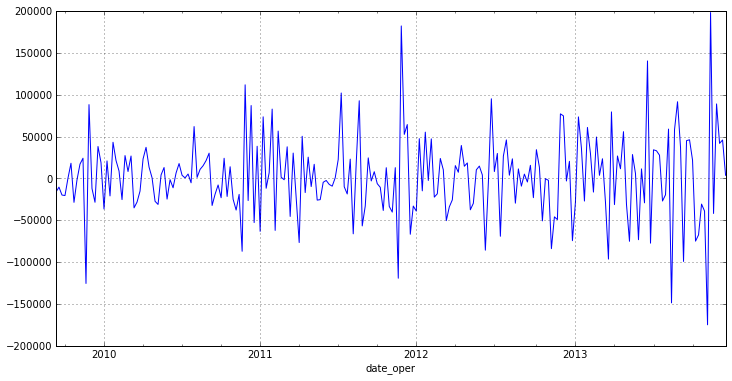
Тренд действительно отсутствует, таким образом ряд первых разностей является стационарным, а наш исходный ряд — интегрированным рядом первого порядка.
Для моделирования будем использовать модель ARIMA, построенную для ряда первых разностей.
Итак, чтобы построить модель нам нужно знать ее порядок, состоящий из 2-х параметров:
Параметр d есть и он равет 1, осталось определить p и q. Для их определения нам надо изучить авторкорреляционную(ACF) и частично автокорреляционную(PACF) функции для ряда первых разностей.
ACF поможет нам определить q, т. к. по ее коррелограмме можно определить количество автокорреляционных коэффициентов сильно отличных от 0 в модели MA
PACF поможет нам определить p, т. к. по ее коррелограмме можно определить максимальный номер коэффициента сильно отличный от 0 в модели AR.
Чтобы построить соответствующие коррелограммы, в пакете statsmodels имеются следующие функции: plot_acf() и plot_pacf(). Они выводят графики ACF и PACF, у которых по оси X откладываются номера лагов, а по оси Y значения соответствующих функций. Нужно отметить, что количество лагов в функциях и определяет число значимых коэффициентов. Итак, наши функции выглядят так:
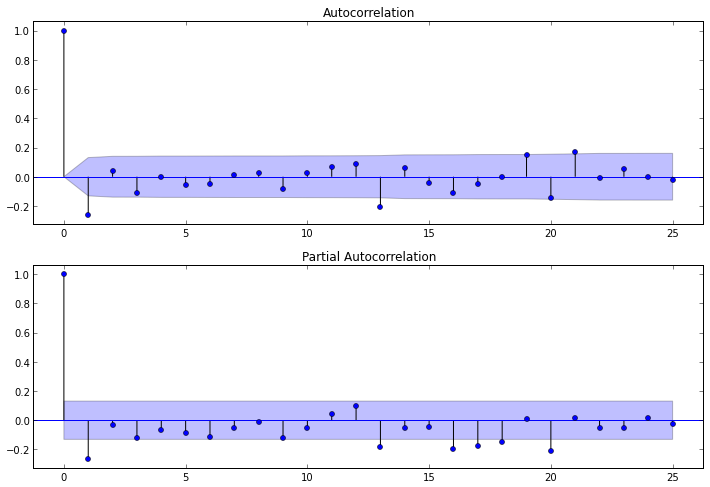
После изучения коррелограммы PACF можно сделать вывод, что p = 1, т.к. на ней только 1 лаг сильно отличнен от нуля. По коррелограмме ACF можно увидеть, что q = 1, т.к. после лага 1 значении функций резко падают.
Итак, когда известны все параметры можно построить модель, но для ее построения мы возмем не все данные, а только часть. Данные из части не попавших в модель мы оставим для проверки точности прогноза нашей модели:
Параметр trend отвечает за наличие константы в моделе. Выведем информацаю по получившейся модели:
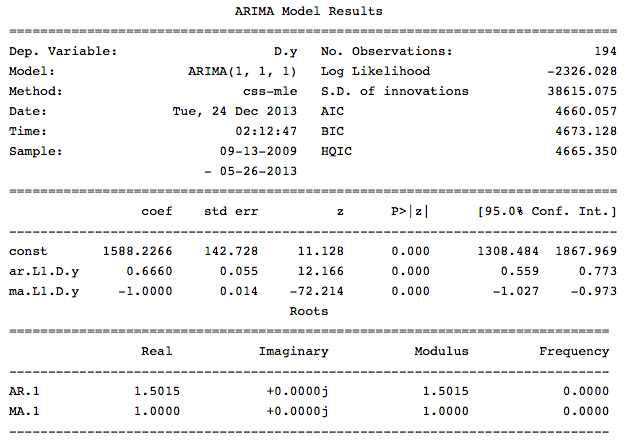
Как видно из данной информации в нашей модели все коэффициенты значимые и можно перейти к оценке модели.
Проверим остатки данной модели на соответствие «белому шуму», а также проанализируем коррелограму остатков, так как это может нам помочь в определении важных для включения и прогнозирования элементов регрессии.
Итак первое, что мы сделаем это проведем Q-тест Льюнга — Бокса для проверки гипотезы о том, что остатки случайны, т. е. являются «белым шумом». Данный тест проводится на остатках модели ARIMA. Таким образом, нам надо сначала получить остатки модели и построить для них ACF, а затем к получившимся коэффициентам приметить тест. С помощью statsmadels это можно сделать так:
Значение данной статистики и p-values, свидетельствуют о том, что гипотеза о случайности остатков не отвергается, и скорее всего данный процесс представляет «белый шум».
Теперь давайте расчитаем коэффициент детерминации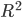 , чтобы понять какой процент наблюдений описывает данная модель:
, чтобы понять какой процент наблюдений описывает данная модель:
R^2: -0.03
Среднеквадратичное отклонение[2] нашей модели:
80919.057367642512
Средняя абсолютная ошибка[2] прогноза:
63092.763277651895
Осталось нарисовать наш прогноз на графике:
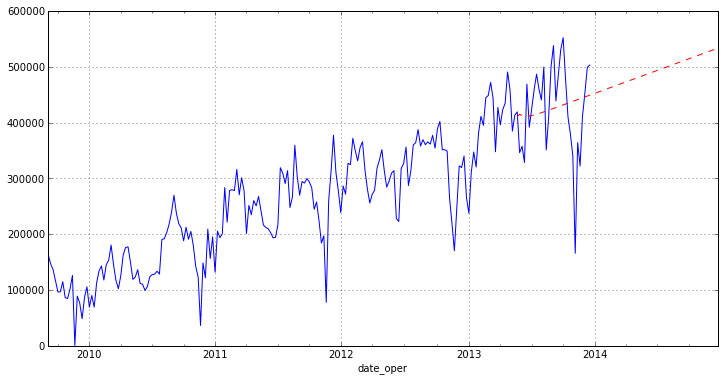
Как можно заметить из графика наша модель строит не очень хороший прогноз. Отчасти это связано с выбросами в исходных данных, которые мы не доконца убрали, а также с модулем ARIMA пакета statsmodels, т. к. он достаточно новый. Статья больше направлена на то, чтобы показать как именно можно анализировать временные ряды на python. Также хотелось бы отметить, что в рассмотреном сегодня пакет очень полно реализованы различные методы регрессионного анализ (постараюсь показать в дальнейших статьях).
В целом для небольших исследований пакет statsmodels в полне пригоден, но для серьезной научной работы все же пока сыроват и некоторые тесты и статистики в нем отсутствуют.
В сегодняшней статье, я попытаюсь описать процесс анализа временных рядов с помощью python и модуля statsmodels. Данный модуль предоставляет широкий набор средств и методов для проведения статистического анализа и эконометрики. Я попытаюсь показать основные этапы анализа таких рядов, в заключении мы построим модель ARIMA.
Для примера взяты реальные данные по товарообороту одного из складских комплексов Подмосковья.
Загрузка и предварительная обработка данных
Для начала загрузим данные и посмотрим на них:
from pandas import read_csv, DataFrame
import statsmodels.api as sm
from statsmodels.iolib.table import SimpleTable
from sklearn.metrics import r2_score
import ml_metrics as metrics
In [2]:
dataset = read_csv('tovar_moving.csv',';', index_col=['date_oper'], parse_dates=['date_oper'], dayfirst=True)
dataset.head()
| Otgruzka | priemka | |
|---|---|---|
| date_oper | ||
| 2009-09-01 | 179667 | 276712 |
| 2009-09-02 | 177670 | 164999 |
| 2009-09-03 | 152112 | 189181 |
| 2009-09-04 | 142938 | 254581 |
| 2009-09-05 | 130741 | 192486 |
Итак, как можно заметить функция read_csv(), в данном случем помимо указания параметров, которые задают используемые колонки и индекс, можно заметить еще 3 параметра для работы с датой. Остановимся на них поподробнее.
parse_dates задает имена столбцов, которые будут преобразованы в тип DateTime. Стоит отметить, что если в данном столбце будут пустые значения парсинг не удастся и вернется столбец типа object. Чтобы этого избежать надо добавить параметр keep_default_na=False.
Заключительный параметр dayfirst указывает функции парсинга, что первое в строке первым идет день, а не наоборот. Если не задать этот параметр, то функция может не правильно преобразовывать даты и путать месяц и день местами. Например 01.02.2013 будет преобразовано в 02-01-2013, что будет неправильно.
Выделим в отдельную серию временной ряд со значениями отгрузкок:
otg = dataset.Otgruzka
otg.head()
| date_oper | |
| 2009-09-01 | 179667 |
| 2009-09-02 | 177670 |
| 2009-09-03 | 152112 |
| 2009-09-04 | 142938 |
| 2009-09-05 | 130741 |
| Name: Otgruzka, dtype: int64 | |
Итак у нас теперь есть временной ряд и можно перейти к его анализу.
Анализ временного ряда
Для начала давайте посмортим график нашего ряда:
otg.plot(figsize=(12,6))

Из графика видно, что наш ряд имеет небольшое кол-во выбросов, которые влияют на разброс. Кроме того анализировать отгрузки за каждый день не совсем верно, т.к., например, в конце или начале недели будут дни в которые товара отгружается значительно больше, нежели в остальные. Поэтому есть смысл перейти к недельному интервалу и среднему значению отгрузок на нем, это избавит нас от выбросов и уменьшит колебания нашего ряда. В pandas для этого есть удобная функция resample(), в качестве параметров ей передается период округления и аггрегатная функция:
otg = otg.resample('W', how='mean')
otg.plot(figsize=(12,6))

Как можно заметить, новый график не имеет ярких выбросов и имеет ярко выраженный тренд. Из это можно сделать вывод о том, что ряд не является стационарным[1].
itog = otg.describe()
otg.hist()
itog
| count | 225 |
| mean | 270858.285365 |
| std | 118371.082975 |
| min | 872.857143 |
| 25% | 180263.428571 |
| 50% | 277898.714286 |
| 75% | 355587.285714 |
| max | 552485.142857 |
| dtype: float64 | |

Как можно заметить из характеристик и гистограммы, ряд у нас более менее однородный и имеет относительно небольшой разброс о чем свидетельствует коэффициент вариации:
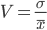 , где
, где 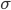 — cреднеквадратическое отклонение,
— cреднеквадратическое отклонение, 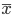 — среднее арифметическое выборки. В нашем случае он равен:
— среднее арифметическое выборки. В нашем случае он равен:print 'V = %f' % (itog['std']/itog['mean'])
V = 0.437022
Проведем тест Харки — Бера для определения номарльности распределения, чтобы подтвердить предположение об однородности. Для этого в существует функция jarque_bera(), которая возвращает значения данной статистики:
row = [u'JB', u'p-value', u'skew', u'kurtosis']
jb_test = sm.stats.stattools.jarque_bera(otg)
a = np.vstack([jb_test])
itog = SimpleTable(a, row)
print itog

Значение данной статистика свидетельствует о том, нулевая гипотеза о нормальности распределения отвергается с малой вероятностью (probably > 0.05), и, следовательно, наш ряд имеет нормального распределения.
Функция SimpleTable() служит для оформления вывода. В нашем случае на вход ей подается массив значений (размерность не больше 2) и список с названиями столбцов или строк.
Многие методы и модели основаны на предположениях о стационарности ряда, но как было замечено ранее наш ряд таковым скорее всего не является. Поэтому для проверки проверки стационарности давайте проведем обобщенный тест Дикки-Фуллера на наличие единичных корней. Для этого в модуле statsmodels есть функция adfuller():
test = sm.tsa.adfuller(otg)
print 'adf: ', test[0]
print 'p-value: ', test[1]
print'Critical values: ', test[4]
if test[0]> test[4]['5%']:
print 'есть единичные корни, ряд не стационарен'
else:
print 'единичных корней нет, ряд стационарен'
adf: -1.38835541357
p-value: 0.58784577297
Critical values: {'5%': -2.8753374677799957, '1%': -3.4617274344627398, '10%': -2.5741240890815571}
есть единичные корни, ряд не стационарен
Проведенный тест подтвердил предположения о не стационарности ряда. Во многих случаях взятие разности рядов позволяет это сделать.Если, например, первые разности ряда стационарны, то он называется интегрированным рядом первого порядка.
Итак, давайте определим порядок интегрированного ряда для нашего ряда:
otg1diff = otg.diff(periods=1).dropna()
В коде выше функция diff() вычисляет разность исходного ряда с рядом с заданным смещением периода. Период смещения передается как параметр period. Т.к. в разности первое значение получиться неопределенным, то нам надо избавиться от него для этого и используется метод dropna().
Проверим получившийся ряд на стационарность:
test = sm.tsa.adfuller(otg1diff)
print 'adf: ', test[0]
print 'p-value: ', test[1]
print'Critical values: ', test[4]
if test[0]> test[4]['5%']:
print 'есть единичные корни, ряд не стационарен'
else:
print 'единичных корней нет, ряд стационарен'
adf: -5.95204224907
p-value: 2.13583392404e-07
Critical values: {'5%': -2.8755379867788462, '1%': -3.4621857592784546, '10%': -2.574231080806213}
единичных корней нет, ряд стационарен
Как видно из кода выше получившийся ряд первых разностей приблизился к стационарному. Для полной уверенности разобъем его на несколько промежутков и убедимся мат. ожидания на разных интервалах:
m = otg1diff.index[len(otg1diff.index)/2+1]
r1 = sm.stats.DescrStatsW(otg1diff[m:])
r2 = sm.stats.DescrStatsW(otg1diff[:m])
print 'p-value: ', sm.stats.CompareMeans(r1,r2).ttest_ind()[1]
p-value: 0.693072039563
Высокое p-value дает нам возможность утверждать, что нулевая гипотеза о равенстве средних верна, что свидетельствует о стационарности ряда. Осталось убедиться в отсутствии тренда для этого построим график нашего нового ряда:
otg1diff.plot(figsize=(12,6))
Тренд действительно отсутствует, таким образом ряд первых разностей является стационарным, а наш исходный ряд — интегрированным рядом первого порядка.
Построение модели временного ряда
Для моделирования будем использовать модель ARIMA, построенную для ряда первых разностей.
Итак, чтобы построить модель нам нужно знать ее порядок, состоящий из 2-х параметров:
Параметр d есть и он равет 1, осталось определить p и q. Для их определения нам надо изучить авторкорреляционную(ACF) и частично автокорреляционную(PACF) функции для ряда первых разностей.
ACF поможет нам определить q, т. к. по ее коррелограмме можно определить количество автокорреляционных коэффициентов сильно отличных от 0 в модели MA
PACF поможет нам определить p, т. к. по ее коррелограмме можно определить максимальный номер коэффициента сильно отличный от 0 в модели AR.
Чтобы построить соответствующие коррелограммы, в пакете statsmodels имеются следующие функции: plot_acf() и plot_pacf(). Они выводят графики ACF и PACF, у которых по оси X откладываются номера лагов, а по оси Y значения соответствующих функций. Нужно отметить, что количество лагов в функциях и определяет число значимых коэффициентов. Итак, наши функции выглядят так:
ig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(otg1diff.values.squeeze(), lags=25, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(otg1diff, lags=25, ax=ax2)
После изучения коррелограммы PACF можно сделать вывод, что p = 1, т.к. на ней только 1 лаг сильно отличнен от нуля. По коррелограмме ACF можно увидеть, что q = 1, т.к. после лага 1 значении функций резко падают.
Итак, когда известны все параметры можно построить модель, но для ее построения мы возмем не все данные, а только часть. Данные из части не попавших в модель мы оставим для проверки точности прогноза нашей модели:
src_data_model = otg[:'2013-05-26']
model = sm.tsa.ARIMA(src_data_model, order=(1,1,1), freq='W').fit(full_output=False, disp=0)Параметр trend отвечает за наличие константы в моделе. Выведем информацаю по получившейся модели:
print model.summary()
Как видно из данной информации в нашей модели все коэффициенты значимые и можно перейти к оценке модели.
Анализ и оценка модели
Проверим остатки данной модели на соответствие «белому шуму», а также проанализируем коррелограму остатков, так как это может нам помочь в определении важных для включения и прогнозирования элементов регрессии.
Итак первое, что мы сделаем это проведем Q-тест Льюнга — Бокса для проверки гипотезы о том, что остатки случайны, т. е. являются «белым шумом». Данный тест проводится на остатках модели ARIMA. Таким образом, нам надо сначала получить остатки модели и построить для них ACF, а затем к получившимся коэффициентам приметить тест. С помощью statsmadels это можно сделать так:
q_test = sm.tsa.stattools.acf(model.resid, qstat=True) #свойство resid, хранит остатки модели, qstat=True, означает что применяем указынный тест к коэф-ам
print DataFrame({'Q-stat':q_test[1], 'p-value':q_test[2]})Результат
| Q-stat | p-value | |
|---|---|---|
| 0 | 0.531426 | 0.466008 |
| 1 | 3.073217 | 0.215109 |
| 2 | 3.644229 | 0.302532 |
| 3 | 3.906326 | 0.418832 |
| 4 | 4.701433 | 0.453393 |
| 5 | 5.433745 | 0.489500 |
| 6 | 5.444254 | 0.605916 |
| 7 | 5.445309 | 0.709091 |
| 8 | 5.900762 | 0.749808 |
| 9 | 6.004928 | 0.814849 |
| 10 | 6.155966 | 0.862758 |
| 11 | 6.299958 | 0.900213 |
| 12 | 12.731542 | 0.468755 |
| 13 | 14.707894 | 0.398410 |
| 14 | 20.720607 | 0.145996 |
| 15 | 23.197433 | 0.108558 |
| 16 | 23.949801 | 0.120805 |
| 17 | 24.119236 | 0.151160 |
| 18 | 25.616184 | 0.141243 |
| 19 | 26.035165 | 0.164654 |
| 20 | 28.969880 | 0.114727 |
| 21 | 28.973660 | 0.145614 |
| 22 | 29.017716 | 0.179723 |
| 23 | 32.114006 | 0.124191 |
| 24 | 32.284805 | 0.149936 |
| 25 | 33.123395 | 0.158548 |
| 26 | 33.129059 | 0.192844 |
| 27 | 33.760488 | 0.208870 |
| 28 | 38.421053 | 0.113255 |
| 29 | 38.724226 | 0.132028 |
| 30 | 38.973426 | 0.153863 |
| 31 | 38.978172 | 0.184613 |
| 32 | 39.318954 | 0.207819 |
| 33 | 39.382472 | 0.241623 |
| 34 | 39.423763 | 0.278615 |
| 35 | 40.083689 | 0.293860 |
| 36 | 43.849515 | 0.203755 |
| 37 | 45.704476 | 0.182576 |
| 38 | 47.132911 | 0.174117 |
| 39 | 47.365305 | 0.197305 |
Значение данной статистики и p-values, свидетельствуют о том, что гипотеза о случайности остатков не отвергается, и скорее всего данный процесс представляет «белый шум».
Теперь давайте расчитаем коэффициент детерминации
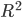 , чтобы понять какой процент наблюдений описывает данная модель:
, чтобы понять какой процент наблюдений описывает данная модель:pred = model.predict('2013-05-26','2014-12-31', typ='levels')
trn = otg['2013-05-26':]
r2 = r2_score(trn, pred[1:32])
print 'R^2: %1.2f' % r2R^2: -0.03
Среднеквадратичное отклонение[2] нашей модели:
metrics.rmse(trn,pred[1:32])80919.057367642512
Средняя абсолютная ошибка[2] прогноза:
metrics.mae(trn,pred[1:32])63092.763277651895
Осталось нарисовать наш прогноз на графике:
otg.plot(figsize=(12,6))
pred.plot(style='r--')
Заключение
Как можно заметить из графика наша модель строит не очень хороший прогноз. Отчасти это связано с выбросами в исходных данных, которые мы не доконца убрали, а также с модулем ARIMA пакета statsmodels, т. к. он достаточно новый. Статья больше направлена на то, чтобы показать как именно можно анализировать временные ряды на python. Также хотелось бы отметить, что в рассмотреном сегодня пакет очень полно реализованы различные методы регрессионного анализ (постараюсь показать в дальнейших статьях).
В целом для небольших исследований пакет statsmodels в полне пригоден, но для серьезной научной работы все же пока сыроват и некоторые тесты и статистики в нем отсутствуют.
Ссылки
- И.И. Елисеева. Эконометрика
- Сравнение моделей временных рядов