 Доброго времени суток читатель. Сегодняшний пост будет посвящен вычислению приближенного значения фрактальной размерности плоского изображения, которая тесно связано с размерности Минковского. Это интересно как минимум по двум причинам. Во-первых оказывается, что размерность ограниченного множества в метрическом пространстве может быть не только целым числом, но и любым неотрицательным. Во-вторых значение размерности контура изображения (а это ограниченное множество в метрическом пространстве) является хорошим признаком. В рамках сегодняшнего поста не предусмотрено исследование робастности этого признака, но давайте рассмотрим показательный пример. Множество различных характеристик клеток опухолей молочной железы, полученное в результате анализа снимков тонкоигольной пункционной биопсии. Множество данных состоит из 30 признаков (поля таблицы) с пометкой злокачественная или доброкачественная опухоль, и одним из признаков является как раз фрактальная размерность ядер клеток опухоли. Под катом вас ждет объяснение смысла фрактальной размерности множества, по возможности доступным языком, алгоритм вычисления приближенного значения этой размерности, его реализация на c# и ряд примеров с картинками. Возможно вы открыли этот пост только из-за картинки справа, это изображение я позаимствовал из инстаграмма Jennifer Selter, и в конце мы вычислим фрактальную размерность, так сказать филейной части Дженифер. Хочется кстати вас попросить ответить на пару вопросов в конце поста.
Доброго времени суток читатель. Сегодняшний пост будет посвящен вычислению приближенного значения фрактальной размерности плоского изображения, которая тесно связано с размерности Минковского. Это интересно как минимум по двум причинам. Во-первых оказывается, что размерность ограниченного множества в метрическом пространстве может быть не только целым числом, но и любым неотрицательным. Во-вторых значение размерности контура изображения (а это ограниченное множество в метрическом пространстве) является хорошим признаком. В рамках сегодняшнего поста не предусмотрено исследование робастности этого признака, но давайте рассмотрим показательный пример. Множество различных характеристик клеток опухолей молочной железы, полученное в результате анализа снимков тонкоигольной пункционной биопсии. Множество данных состоит из 30 признаков (поля таблицы) с пометкой злокачественная или доброкачественная опухоль, и одним из признаков является как раз фрактальная размерность ядер клеток опухоли. Под катом вас ждет объяснение смысла фрактальной размерности множества, по возможности доступным языком, алгоритм вычисления приближенного значения этой размерности, его реализация на c# и ряд примеров с картинками. Возможно вы открыли этот пост только из-за картинки справа, это изображение я позаимствовал из инстаграмма Jennifer Selter, и в конце мы вычислим фрактальную размерность, так сказать филейной части Дженифер. Хочется кстати вас попросить ответить на пару вопросов в конце поста.Размерность
Как обычно для того что бы понять смысл алгоритма, необходимо немного окунуться в теорию. Википедия сообщает нам, что размерность в физике (и скорее всего большинство людей именно так воспринимают смысл размерности) — это количество независимых параметров, необходимых для описания состояния объекта, или количество степеней свободы физической системы. Но в математике все обстоит немного по-другому, тут у нас есть ряд определений размерности, которые часто зависят от рабочего пространства. В рамках общей топологии дается несколько определений размерности, и из них нам интересны будут размерность Хаусдорфа, размерность Минковского и фрактальная размерность.
Для начала вспомним формальный смысл тех размерностей, которые для нас интуитивно понятны, в векторном пространстве которое нас окружает. Под базисом векторного пространства мы понимаем максимальное множество линейно не зависимых векторов. Количество этих векторов мы называем размерностью векторного пространства, или его рангом. И любой элемент векторного пространства можно представить в виде линейной комбинации базисных векторов.
Размерность Хаусдорфа
Размерность Хаусдорфа обобщает понятие размерности действительного векторного пространства, и является естественным способом определения размерности подмножества в метрическом пространстве. Например размерность Хаусдорфа n-мерного (размерность в смысле векторного пространства) унитарного пространства (особый случай векторного пространства) будет тоже равна n. Хорошее математическое описание размерности Хаусдорфа дано в русской википедии, нам же важно понять смысл этой размерности интуитивно. Представим полное покрытие множества X шарами радиуса не более чем r, обозначим количество этих шаров за N( r ).

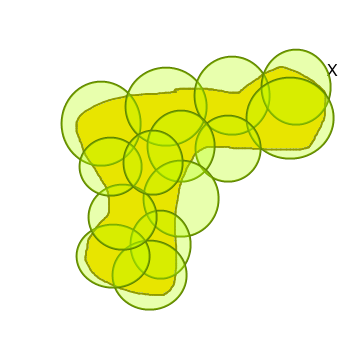
Значение N( r ) будет расти при уменьшении r (для полного покрытия будет требоваться все больше шаров). Размерностью Хаусдорфа хорошего множества X будет являться такое уникальное число d, что N( r ) будет расти как 1/rd при стремлении r к нулю. Под хорошим множеством понимаются гладкие множества без особенностей, какими например обладают фракталы. Примерами хороших множеств могут быть любые идеализированные геометрические объекты такие как куб, сфера и так далее.
Фрактальная размерность
Опишем один простой способ задания фрактальной размерности, хотя например размерность Минковского так же является одой из фрактальных размерностей, и она как раз тесно связана с размерностью Хаусдорфа, но об этом позже. Вот он простой способ задания фрактальной размерности:
- Возьмем некоторую D-мерную геометрическую структуру и будем делить итеративно ее стороны на M равных частей (на следующей итерации, будем делить каждую полученную на предыдущей итерации часть так же на M частей)
- Каждый уровень будет состоять из MD частей предыдущего уровня
- Обозначим следующим образом количество полученных частей N = MD
Выполним следующее преобразование для вычисления формулы для значения фрактальной размерности D:

Рассмотрим простые примеры, которые я почерпнул из очень крутого курса по комплексным системам. Возьмем отрезок (одномерное ограниченное множество), разделим его на две равные части, таким же образом будем поступать с каждой полученной частью. Таким образом мы будем создавать полное покрытие множества.

Т.е. M = 2 и N = 2, т.к. из каждой части производится два новых куска отрезка, вычислим D:

Если разделять отрезок не на 2 части, а на 3, то D все равно будет равна 1, т.к. M = 3 и N = 3. Эта размерность совпадает с размерностью Хаусдорфа для хорошего множества.
Давайте рассмотрим аналогичную процедуру для квадрата.
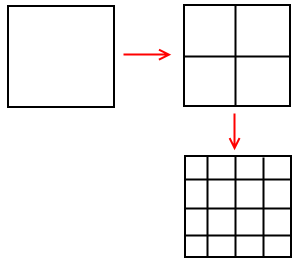
Получаем M = 2 и N = 4, т.к. разделяя стороны на 2 равные части, мы получаем 4 новых, вычислим фрактальную размерность
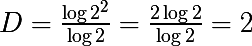
И опять полученная размерность совпала с размерностью Хаусдорфа. Такой же результат можно получить если делить стороны на 3 равные части и т.д.
Бенуа Мандельброт при исследовании реальных объектов сделал очевидное замечание:
clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line
В реальном мире мы редко имеем дело с идеализированными объектами, что же будет если мы рассмотрим не совсем хороший геометрический объект, например кривую Коха (не путать с палочкой), вспомним алгоритм генерации такого множества. На каждой новой итерации, каждый кусок кривой, который является прямым отрезком, делится на три равные части, затем средний кусок убирается, а на его место становится конструкция напоминающая перевернутую букву V, каждое ребро которой равно убранной части отрезка (а так же равно и оставшимся).
Другими словами M = 3, т.к. отрезок делится на три равные части, а N = 4, т.к. каждая часть превращается в 4 части равных 1/4 от оригинала. Тогда фрактальная размерность такого множества при бесконечном итерировании будет равна следующему значению:

В качестве другого примера давайте глянем на треугольник Серпинского

На каждой итерации одна сторона делится на 2 части, т.е. M = 2, а в результате получается 3 части, т.е. N = 3, тогда

Возникает конечно вопрос, вот мы получили цифры некоторые, ну размерность стала дробной, и что? Есть ли в этом какой-то смысл, или это просто математические штучки. Строгой формулировки с описанием смысла дробности размерности нет, но можно ее интерпретировать следующим образом, на некотором интуитивном уровне. Фрактальная размерность чувствительна
ко всякого рода несовершенствам реальных объектов, позволяя различать и индивидуализировать то, что прежде было безлико и неразличимо (источник)
В курсе по анализу комплексных систем упоминается следующая трактовка: дробная размерность — это своего рода плотность самоподобия.
Но говоря о реальных объектах читатель сразу же скажет, но ведь и кривая Коха и треугольник Серпинского далеки от реальности, что же делать тогда? Как я упомянул выше, приведенное определение фрактальной размерности является простым, и одним из нескольких. Давайте перейдем к более сложному определению фрактальной размерности. А пока взгляните, например, на капусту брокколи Романеско, вот такая вот реальность.

Размерность Минковского
Размерность Минковского — это один из способов задания фрактальной размерности ограниченного множества в метрическом пространстве, определяется следующим образом:

- где N(ε) минимальное число множеств диаметра ε, которыми можно покрыть исходное множество.
Если предел не существует, то рассматривают верхний и нижний пределы и говорят соответственно о верхней и нижней размерности Минковского. Верхняя и нижняя размерности Минковского тесно связанны с размерностью Хаусдорфа, интуитивно это легко уловить по способу задания размерности. Обычно упомянутые три размерности совпадают, и только в очень специфичных случаях имеет смысл их различать, но это не наши случаи.
Размерность Минковского имеет так же другое название — box-counting dimension, из-за альтернативного способа ее определения, который кстати дает подсказку к способу вычисления этой самой размерности. Рассмотрим двумерный случай, хотя аналогичное определение распространяется и на n-мерный случай. Возьмем некоторое ограниченное множество в метрическом пространстве, например черно-белую картинку, нарисуем на ней равномерную сетку с шагом ε, и закрасим те ячейки сетки, которые содержат хотя бы один элемент искомого множества.

Далее начнем уменьшать размер ячеек, т.е. ε, тогда размерность Минковского будет вычисляться по вышеприведенной формуле, исследуя скорость изменения отношения логарифмов. Эта фраза может быть не сразу понятна, но думаю все прояснит алгоритм, используемый для вычисления приближенного значения размерности Минковского.
Box-counting алгоритм
Алгоритм выводится следующим образом, обозначим за Dbc приближенное значение размерности Минковского. Запишем определение этой размерности, убрав предел, его мы будем имитировать в итерациях, в которых будет изменяться размер ячеек.
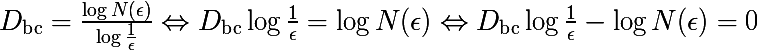
Если зафиксировать размеры ячеек ε и рассматривать Dbc как неизвестное, то легко заметить, что приведенное выражение является формулой линии. Мы можем запустить цикл по различным размерам ячеек ε и записывать результат. Давайте нанесем эти результаты на график и построим линию регрессии для полученного множества данных, это значение и будет являться аппроксимацией фрактальной размерности Минковского.

Вот кстати список объектов с их фрактальными размерностями.
Надеюсь у меня получилось передать связь между естественной размерностью, и тем каким образом и зачем люди пришли к другим определениям размерности. Давайте перейдем к коду, а затем к примерам.
Box-counting алгоритм, C# код
Для вычисления размерности Минковского нам необходимы будут две процедуры, начнем с линейной регрессии. Вообще решить задачу линейной регрессии можно различными способами, чаще всего для этого используется метод градиентного спуска и метод наименьших квадратов (Normal equations). Первый хорошо работает на больших и широких данных, второй слабоват на широких данных из-за необходимости вычислять обратную матрицу, ширина которой равна ширине массива данных. В нашем случае ширина всего 2, так что это наш случай. В векторизованном виде решение линейной регрессии записывается следующим образом:
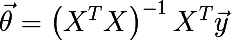
Обратную матрицу будем искать по следующей формуле:

Normal equations
public static double[] NormalEquations2d(double[] y, double[] x)
{
//x^t * x
double[,] xtx = new double[2, 2];
for (int i = 0; i < x.Length; i++)
{
xtx[0, 1] += x[i];
xtx[0, 0] += x[i] * x[i];
}
xtx[1, 0] = xtx[0, 1];
xtx[1, 1] = x.Length;
//inverse
double[,] xtxInv = new double[2, 2];
double d = 1/(xtx[0, 0]*xtx[1, 1] - xtx[1, 0]*xtx[0, 1]);
xtxInv[0, 0] = xtx[1, 1]*d;
xtxInv[0, 1] = -xtx[0, 1]*d;
xtxInv[1, 0] = -xtx[1, 0]*d;
xtxInv[1, 1] = xtx[0, 0]*d;
//times x^t
double[,] xtxInvxt = new double[2, x.Length];
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < x.Length; j++)
{
xtxInvxt[i, j] = xtxInv[i, 0]*x[j] + xtxInv[i, 1];
}
}
//times y
double[] theta = new double[2];
for (int i = 0; i < 2; i++)
{
for (int j = 0; j < x.Length; j++)
{
theta[i] += xtxInvxt[i, j]*y[j];
}
}
return theta;
}
В нулевом элементе выходного вектора содержится угловой коэффициент (это и будет искомая размерность Минковского), а в следующем элементе — смещение. И собственно ключевая функция, которая возвращает датасет, по которому необходимо вычислить угловой коэффициент
Box-counting
/// <summary>
/// Box-counting algorithm
/// </summary>
/// <param name="bw">black-white bitmap</param>
/// <param name="startSize">initial size of square of grid</param>
/// <param name="finishSize">final size of square of grid</param>
/// <param name="step">step of changing of the grid</param>
/// <returns>baList.Add(Math.Log(1d/b), Math.Log(a)), where b is swuare length size, a is the number of intersection of image with grid squares</returns>
public static IDictionary<double, double> BowCountingDimension(BwBitmap bw, int startSize, int finishSize, int step = 1,
string dataPath = "")
{
//length size - number of boxes
IDictionary<double, double> baList = new Dictionary<double, double>();
for (int b = startSize; b <= finishSize; b += step)
{
int hCount = bw.Height/b;
int wCount = bw.Width/b;
bool[,] filledBoxes =
new bool[wCount + (bw.Width > wCount*b ? 1 : 0), hCount + (bw.Height > hCount*b ? 1 : 0)];
for (int x = 0; x < bw.Width; x++)
{
for (int y = 0; y < bw.Height; y++)
{
if (bw.GetBwPixel(x, y))
{
int xBox = x/b;
int yBox = y/b;
filledBoxes[xBox, yBox] = true;
}
}
}
int a = 0;
for (int i = 0; i < filledBoxes.GetLength(0); i++)
{
for (int j = 0; j < filledBoxes.GetLength(1); j++)
{
if (filledBoxes[i, j])
{
a++;
}
}
}
baList.Add(Math.Log(1d/b), Math.Log(a));
if (dataPath.Length > 0)
{
if (dataPath[dataPath.Length - 1] != '\\')
{
dataPath += '\\';
}
if (Directory.Exists(dataPath))
{
XBitmap bmp = new XBitmap(bw);
for (int i = 0; i < filledBoxes.GetLength(0); i++)
{
bmp.DrawLine(i * b, 0, i * b, bmp.Height, Color.HotPink);
}
for (int j = 0; j < filledBoxes.GetLength(1); j++)
{
bmp.DrawLine(0, j * b, bmp.Width, j * b, Color.HotPink);
}
for (int i = 0; i < filledBoxes.GetLength(0); i++)
{
for (int j = 0; j < filledBoxes.GetLength(1); j++)
{
if (filledBoxes[i, j])
{
bmp.FillRectangle(i * b, j * b, i * b + b, j * b + b, Color.Red, 2);
}
}
}
bmp.ConvertToNativeBitmap().Save(dataPath + b + ".bmp");
}
}
Logger.Instance.Log("BoxCounting: b is " + b + " of " + finishSize);
}
if (dataPath.Length > 0)
{
using (StreamWriter sw = new StreamWriter(dataPath + "ba.csv"))
{
sw.WriteLine("NumberOfBoxes,LengthOfSideInv");
foreach (double bInv in baList.Keys)
{
sw.WriteLine(baList[bInv] + "," + bInv);
}
sw.Close();
}
}
return baList;
}
Остается только связать две процедуры:
IDictionary<double, double> baList = BowCountingDimension(bwContour, 5, 100, 1, dir + "boxing\\");
double[] y = new double[baList.Count];
double[] x = new double[baList.Count];
int c = 0;
foreach (double key in baList.Keys)
{
y[c] = baList[key];
x[c] = key;
c++;
}
double[] theta = NormalEquations2d(y, x);
Примеры
Буква
Рассмотрим простое изображение без особенностей, т.е. с гладкими краями. В компьютерном зрении часто анализируется не изображение целиком, а его контур.

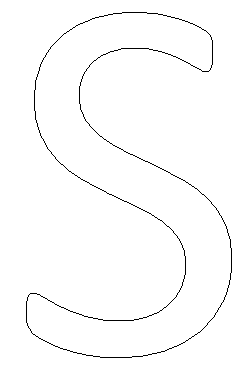


Фрактальная размерность в районе единицы сообщает нам о том, что фигура действительно без особенностей, и вполне гладкая.
Кривая Коха

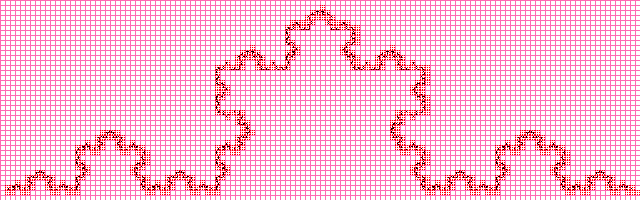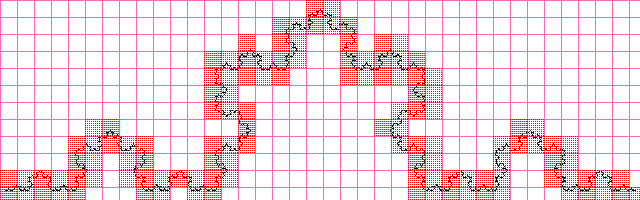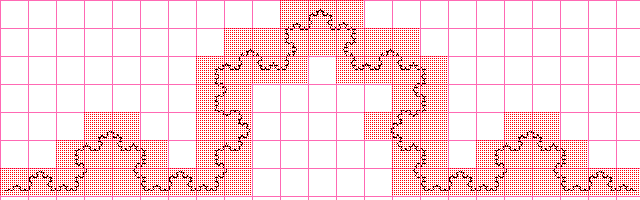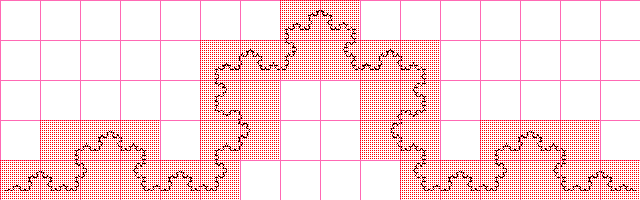

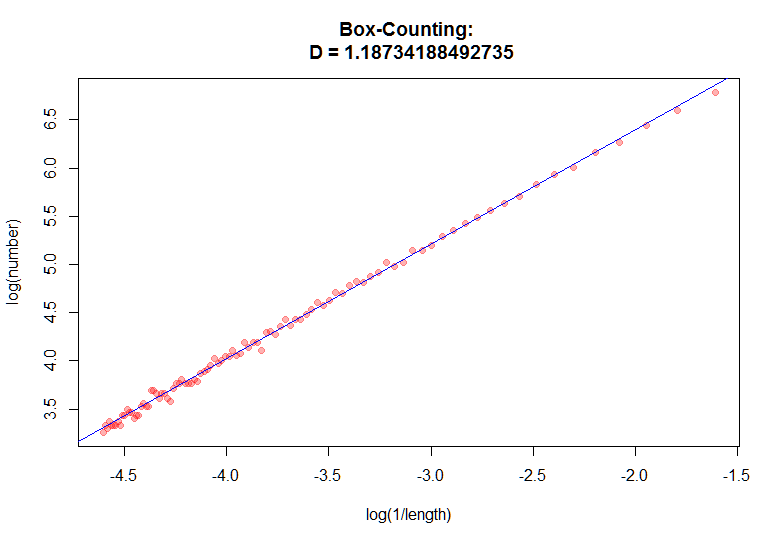
Значение получилось почти такое же как и при вычислении фрактальной размерности аналитически, очевидно, что при увеличении разрешения изображения, аппроксимированное значение будет приближаться к вычисленному аналитически.
JanSetler




Карта России
Возьмем что нибудь более изрезанное, например карту нашей страны.

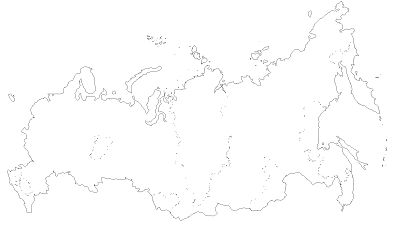

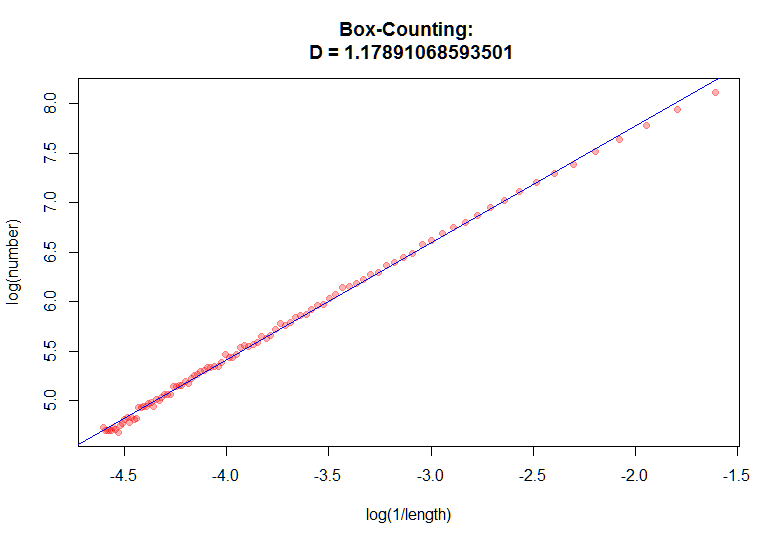
Получается что попа Дженифеер немного интереснее контура России, ну что ж поделать.
Фрактал
А будет ли значительно отличаться значение размерности для фрактала? Давайте проверим. Рассмотрим одно из множеств Жюлиа, точнее его границу. Гифку пришлось порезать, т.к. программка не справлялась с высоким разрешением, а масштабирование затирало сетку.


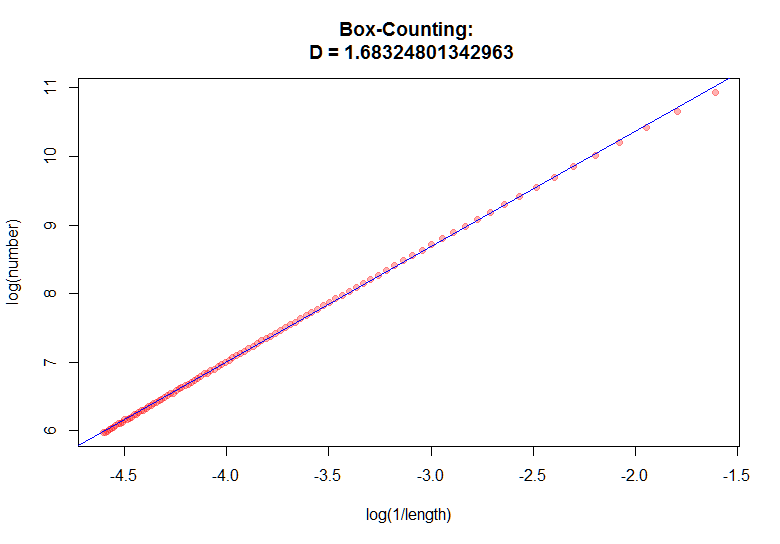
Как видите фрактал интереснее даже чем попа Дженифер.
Ссылки
Всю инфу вы найдете по ссылкам выше, в конце же я повторюсь только насчет двух курсов, второй кстати начался только пару дней назад, так что всем советую.
Как то я в послал письмо одминам хабра с просьбой создать хаб по машинному обучению, получил такой вот ответ «Если наберется постов 15-20, которые просто обязаны быть в этом хабе — подумаем». Вообще таких постов уже давно больше, чем 15-20, у меня их только минимум штук 10. Я понимаю, что одминистрация больше занята хабами с политотой, но может попробуем обратить их внимание на действительно важные хабы.
Only registered users can participate in poll. Log in, please.
Нужен ли отдельный хаб по машинному обучению?
89.42% да786
10.58% нет93
879 users voted. 204 users abstained.
Only registered users can participate in poll. Log in, please.
Нужен ли отдельный хаб по компьютерному зрению?
80.04% да730
19.96% нет182
912 users voted. 202 users abstained.