Как упоминалось в предыдущей статье, латентно-семантический анализ (ЛСА / LSA) позволяет выявлять латентные связи изучаемых явлений или объектов, что является немаловажным критерием при моделировании процессов понимания и мышления.
Теперь я напишу немного о реализации ЛСА.
ЛСА был запатентован в 1988 году группой американских инжинеров-исследователей S.Deerwester at al [U.S. Patent 4,839,853 ].
В области информационного поиска данный подход называют латентно-семантическим индексированием (ЛСИ).
Впервые ЛСА был применен для автоматического индексирования текстов, выявления семантической структуры текста и получения псевдодокументов. Затем этот метод был довольно успешно использован для представления баз знаний и построения когнитивных моделей. В США этот метод был запатентован для проверки знаний школьников и студентов, а так же проверки качества обучающих методик.
В качестве исходной информации ЛСА использует матрицу термы-на-документы (термы – слова, словосочетания или н-граммы; документы – тексты, классифицированные либо по какому-либо критерию, либо разделенные произвольным образом – это зависит от решаемой задачи), описывающую набор данных, используемый для обучения системы. Элементы этой матрицы содержат, как правило, веса, учитывающие частоты использования каждого терма в каждом документе или вероятностные меры (PLSA – вероятностный латентно-семантический анализ), основанные на независимом мультимодальном распределении.
Наиболее распространенный вариант ЛСА основан на использовании разложения вещественнозначной матрицы по сингулярным значениям или SVD-разложения (SVD – Singular Value Decomposition). С помощью него любую матрицу можно разложить в множество ортогональных матриц, линейная комбинация которых является достаточно точным приближением к исходной матрице.
Согласно теореме о сингулярном разложении в самом простом случае матрица может быть разложена на произведение трех матриц:

где матрицы U и V – ортогональные, а S – диагональная матрица, значения на диагонали которой называются сингулярными значениями матрицы A.
Символ Т в обозначении матрицы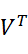 означает транспонирование матрицы.
означает транспонирование матрицы.
Особенность такого разложения в том, что если в матрице S оставить только k наибольших сингулярных значений, то линейная комбинация получившихся матриц будет наилучшим приближением исходной матрицы A к матрице Ă ранга k:
будет наилучшим приближением исходной матрицы A к матрице Ă ранга k:

Основная идея латентно-семантического анализа состоит в следующем:
после перемножения матриц полученная матрица Ă, содержащая только k первых линейно независимых компонент исходной матрицы A, отражает структуру зависимостей (в данном случае ассоциативных), латентно присутствующих в исходной матрице. Структура зависимостей определяется весовыми функциями термов для каждого документа.
Выбор k зависит от поставленной задачи и подбирается эмпирически. Он зависит от количества исходных документов.
Если документов не много, например сотня, то k можно брать 5-10% от общего числа диагональных значений; если документов сотни тысяч, то берут 0,1-2%. Следует помнить, что если выбранное значение k слишком велико, то метод теряет свою мощность и приближается по характеристикам к стандартным векторным методам. А слишком маленькое значение k не позволяет улавливать различия между похожими термами или документами: останется только одна главная компонента, которая «перетянет на себя одеяло», т.е. все слабо и даже несвязанные термы.

Рисунок 1. SVD-разложение матрицы А размерности (T X D) на матрицу термов U размерности (T X k), матрицу документов V размерности (k X D) и диагональную матрицу S размерности (k X k), где k – количество сингулярных значении диагональной матрицы S.
Объем корпуса для построения модели должен быть большим – желательно около трех-пяти миллионов словоупотреблений. Но метод работает и на коллекциях меньшего объема, правда несколько хуже.
Произвольное разбиение текста на документы обычно производят от тысячи до нескольких десятков тысяч частей примерно одинакового объема. Таким образом, матрица термы-на-документы получается прямоугольной и может быть сильно разраженной. Например, при объеме 5 млн. словоформ получается матрица 30-50 тысяч документов на 200-300 тысяч, а иногда и более, термов. В действительности, низкочастотные термы можно опустить, т.к. это заметно снизит размерность матрицы (скажем, если не использовать 5% от общего объема низкочастотных термов, то размерность сократиться в два раза), что приведет к снижению вычислительных ресурсов и времени.
Выбор сокращения сингулярных значений диагональной матрицы (размерности k) при обратном перемножении матриц, как я писал, дело произвольное. При вышеуказанной размерности матрицы оставляют несколько сотен (100-300) главных компонент. При этом, как показывает практика, зависимость количества компонент и точность меняются нелинейно: например, если начинать увеличивать их число, то точность будет падать, но при некотором значении, скажем, 10000 – опять вырастет до оптимального случая.
Ниже приведен пример возникновения и изменения главных факторов при уменьшении числа сингулярных элементов диагональной матрицы.
Точность можно оценивать на размеченном материале, например, заранее скорректировав результат по hсоответствию ответов на вопросы.
Более подробная информация об этом методе содержится, например, в обзорных статьях [см. список литературы].
Желающие попробовать работу LSA могут скачать бинарники для построения моделей и для их проверки и использования.
В программе для SVD разложения матрицы при построении моделей использован открытый код (Copyright Sergey Bochkanov (ALGLIB project).), поэтому программы распространяются без ограничений.
Так же иногда этот метод используют для нахождения «ближайшего соседа» — наиболее близких по весу термов, ассоциативно связанных с исходным. Это свойство используют для поиска близких по смыслу термов.
Следует уточнить, что близость по смыслу – это контекстнозависимая величина, поэтому не всякий близкий терм будет соответствовать ассоциации (это может быть и синоним, и антоним, и просто часто встречающееся вместе с искомым термом слово или словосочетание).
Достоинством метода можно считать его замечательную способность выявлять зависимости между словами, когда обычные статистические методы бессильны. ЛСА также может быть применен как с обучением (с предварительной тематической классификацией документов), так и без обучения (произвольное разбиение произвольного текста), что зависит от решаемой задачи.
Об основных недостатках я писал в предыдущей статье. К ним можно добавить значительное снижение скорости вычисления при увеличении объема входных данных (в частности, при SVD-преобразовании).
Как показано в [Deerwester et al.], скорость вычисления соответствует порядку , где
, где  — сумма количества документов и термов, k– размерность пространства факторов.
— сумма количества документов и термов, k– размерность пространства факторов.

На рисунках показано возникновение и изменение главных факторов при уменьшении числа сингулярных элементов диагональной матрицы от 100% до ~12%. Трехмерные рисунки представляют собой симметричную матрицу, полученную в результате вычисления скалярного произведения векторов каждого эталонного документа с каждым тестируемым. Эталонный набор векторов – это заранее размеченный на 30 документов текст; тестируемый – с уменьшением числа сингулярных значений диагональной матрицы, полученной при SVD-анализе. На осях X и Y откладывается количество документов (эталонных и тестируемых), на оси Z – объем лексикона.
На рисунках хорошо видно, что при уменьшении числа сингулярных диагональных элементов на 20-30% факторы еще не достаточно ярко выявлены, но при этом возникают корреляции похожих документов (небольшие пики вне диагонали), которые сначала незначительно увеличиваются, а затем, с уменьшением числа сингулярных значений (до 70-80%) – исчезают. При автоматической кластеризации такие пики являются шумом, поэтому их желательно минимизировать. Если же целью является получение ассоциативных связей внутри документов, то следует найти оптимальное соотношение сохранения основного лексикона и примешивания ассоциативного.
Теперь я напишу немного о реализации ЛСА.
Немного истории
ЛСА был запатентован в 1988 году группой американских инжинеров-исследователей S.Deerwester at al [U.S. Patent 4,839,853 ].
В области информационного поиска данный подход называют латентно-семантическим индексированием (ЛСИ).
Впервые ЛСА был применен для автоматического индексирования текстов, выявления семантической структуры текста и получения псевдодокументов. Затем этот метод был довольно успешно использован для представления баз знаний и построения когнитивных моделей. В США этот метод был запатентован для проверки знаний школьников и студентов, а так же проверки качества обучающих методик.
Описание работы ЛСА
В качестве исходной информации ЛСА использует матрицу термы-на-документы (термы – слова, словосочетания или н-граммы; документы – тексты, классифицированные либо по какому-либо критерию, либо разделенные произвольным образом – это зависит от решаемой задачи), описывающую набор данных, используемый для обучения системы. Элементы этой матрицы содержат, как правило, веса, учитывающие частоты использования каждого терма в каждом документе или вероятностные меры (PLSA – вероятностный латентно-семантический анализ), основанные на независимом мультимодальном распределении.
Наиболее распространенный вариант ЛСА основан на использовании разложения вещественнозначной матрицы по сингулярным значениям или SVD-разложения (SVD – Singular Value Decomposition). С помощью него любую матрицу можно разложить в множество ортогональных матриц, линейная комбинация которых является достаточно точным приближением к исходной матрице.
Согласно теореме о сингулярном разложении в самом простом случае матрица может быть разложена на произведение трех матриц:

где матрицы U и V – ортогональные, а S – диагональная матрица, значения на диагонали которой называются сингулярными значениями матрицы A.
Символ Т в обозначении матрицы
Особенность такого разложения в том, что если в матрице S оставить только k наибольших сингулярных значений, то линейная комбинация получившихся матриц
 будет наилучшим приближением исходной матрицы A к матрице Ă ранга k:
будет наилучшим приближением исходной матрицы A к матрице Ă ранга k:
Основная идея латентно-семантического анализа состоит в следующем:
после перемножения матриц полученная матрица Ă, содержащая только k первых линейно независимых компонент исходной матрицы A, отражает структуру зависимостей (в данном случае ассоциативных), латентно присутствующих в исходной матрице. Структура зависимостей определяется весовыми функциями термов для каждого документа.
Выбор k зависит от поставленной задачи и подбирается эмпирически. Он зависит от количества исходных документов.
Если документов не много, например сотня, то k можно брать 5-10% от общего числа диагональных значений; если документов сотни тысяч, то берут 0,1-2%. Следует помнить, что если выбранное значение k слишком велико, то метод теряет свою мощность и приближается по характеристикам к стандартным векторным методам. А слишком маленькое значение k не позволяет улавливать различия между похожими термами или документами: останется только одна главная компонента, которая «перетянет на себя одеяло», т.е. все слабо и даже несвязанные термы.

Рисунок 1. SVD-разложение матрицы А размерности (T X D) на матрицу термов U размерности (T X k), матрицу документов V размерности (k X D) и диагональную матрицу S размерности (k X k), где k – количество сингулярных значении диагональной матрицы S.
Объем корпуса для построения модели должен быть большим – желательно около трех-пяти миллионов словоупотреблений. Но метод работает и на коллекциях меньшего объема, правда несколько хуже.
Произвольное разбиение текста на документы обычно производят от тысячи до нескольких десятков тысяч частей примерно одинакового объема. Таким образом, матрица термы-на-документы получается прямоугольной и может быть сильно разраженной. Например, при объеме 5 млн. словоформ получается матрица 30-50 тысяч документов на 200-300 тысяч, а иногда и более, термов. В действительности, низкочастотные термы можно опустить, т.к. это заметно снизит размерность матрицы (скажем, если не использовать 5% от общего объема низкочастотных термов, то размерность сократиться в два раза), что приведет к снижению вычислительных ресурсов и времени.
Выбор сокращения сингулярных значений диагональной матрицы (размерности k) при обратном перемножении матриц, как я писал, дело произвольное. При вышеуказанной размерности матрицы оставляют несколько сотен (100-300) главных компонент. При этом, как показывает практика, зависимость количества компонент и точность меняются нелинейно: например, если начинать увеличивать их число, то точность будет падать, но при некотором значении, скажем, 10000 – опять вырастет до оптимального случая.
Ниже приведен пример возникновения и изменения главных факторов при уменьшении числа сингулярных элементов диагональной матрицы.
Точность можно оценивать на размеченном материале, например, заранее скорректировав результат по hсоответствию ответов на вопросы.
Более подробная информация об этом методе содержится, например, в обзорных статьях [см. список литературы].
Желающие попробовать работу LSA могут скачать бинарники для построения моделей и для их проверки и использования.
В программе для SVD разложения матрицы при построении моделей использован открытый код (Copyright Sergey Bochkanov (ALGLIB project).), поэтому программы распространяются без ограничений.
Применение
- сравнение двух термов между собой;
- сравнение двух документов между собой;
- сравнение терма и документа.
Так же иногда этот метод используют для нахождения «ближайшего соседа» — наиболее близких по весу термов, ассоциативно связанных с исходным. Это свойство используют для поиска близких по смыслу термов.
Следует уточнить, что близость по смыслу – это контекстнозависимая величина, поэтому не всякий близкий терм будет соответствовать ассоциации (это может быть и синоним, и антоним, и просто часто встречающееся вместе с искомым термом слово или словосочетание).
Достоинства и недостатки ЛСА
Достоинством метода можно считать его замечательную способность выявлять зависимости между словами, когда обычные статистические методы бессильны. ЛСА также может быть применен как с обучением (с предварительной тематической классификацией документов), так и без обучения (произвольное разбиение произвольного текста), что зависит от решаемой задачи.
Об основных недостатках я писал в предыдущей статье. К ним можно добавить значительное снижение скорости вычисления при увеличении объема входных данных (в частности, при SVD-преобразовании).
Как показано в [Deerwester et al.], скорость вычисления соответствует порядку
 , где
, где  — сумма количества документов и термов, k– размерность пространства факторов.
— сумма количества документов и термов, k– размерность пространства факторов.Небольшой демо-пример расчета матрицы близости полнотекстовых документов при разном количестве сингулярных элементов диагональной матрицы в SVD-преобразовании

На рисунках показано возникновение и изменение главных факторов при уменьшении числа сингулярных элементов диагональной матрицы от 100% до ~12%. Трехмерные рисунки представляют собой симметричную матрицу, полученную в результате вычисления скалярного произведения векторов каждого эталонного документа с каждым тестируемым. Эталонный набор векторов – это заранее размеченный на 30 документов текст; тестируемый – с уменьшением числа сингулярных значений диагональной матрицы, полученной при SVD-анализе. На осях X и Y откладывается количество документов (эталонных и тестируемых), на оси Z – объем лексикона.
На рисунках хорошо видно, что при уменьшении числа сингулярных диагональных элементов на 20-30% факторы еще не достаточно ярко выявлены, но при этом возникают корреляции похожих документов (небольшие пики вне диагонали), которые сначала незначительно увеличиваются, а затем, с уменьшением числа сингулярных значений (до 70-80%) – исчезают. При автоматической кластеризации такие пики являются шумом, поэтому их желательно минимизировать. Если же целью является получение ассоциативных связей внутри документов, то следует найти оптимальное соотношение сохранения основного лексикона и примешивания ассоциативного.
ЛИТЕРАТУРА
- Thomas Landauer, Peter W. Foltz, & Darrell Laham (1998). «Introduction to Latent Semantic Analysis» (PDF). Discourse Processes 25: 259–284. U.S. Patent 4,839,853 (англ.)
- Scott Deerwester, Susan T. Dumais, George W. Furnas, Thomas K. Landauer, Richard Harshman (1990). «Indexing by Latent Semantic Analysis» (PDF). Journal of the American Society for Information Science 41 (6): 391–407.
- Thomas Landauer, Susan T. Dumais A Solution to Plato's Problem: The Latent Semantic Analysis Theory of Acquisition, Induction, and Representation of Knowledge 211–240 (1997). Проверено 2 июля 2007.
- B. Lemaire, G. Denhière Cognitive Models based on Latent Semantic Analysis (2003).
- Некрестьянов И.С. Тематико-ориентированные методы информационного поиска / Диссертация на соискание степени к. ф-м.н. СПбГУ, 2000.
- Соловьев А.Н. Моделирование процессов понимания речи с использованием латентно-семантического анализа / Диссертация на соискание степени к. ф-м.н. СПбГУ, 2008.
- Голуб Дж., Ван Лоун Ч. Матричные вычисления. М.: «Мир», 1999.
Ссылки
- webcom.upmf-grenoble.fr/LPNC/resources/benoit_lemaire/lsa.html – Readings in Latent Semantic Analysis for Cognitive Science and Education. – Сборник статей и ссылок о ЛСА.
- lsa.colorado.edu – сайт, посвященный моделированию ЛСА.
- www.cs.utk.edu/%7Elsi – Latent Semantic Indexing (Латенто-семантическое индексирование).
- archive.today/1AnaN – Telcordia Latent Semantic Indexing (LSI). Demo Machine – Демонстрационный сайт латентно-семантического индексирования.
- cran.at.r-project.org/web/packages/lsa/index.html — Open Source LSA Package