Содержание
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
- Свойства тензора инерции твердого тела
- Зарисовка о гайке Джанибекова
- Математическое моделирование эффекта Джанибекова
Введение
В этой статье мы продолжим тему, начатую предыдущей публикацией. В прошлый раз мы, с помощью тензоров, выявили природу угловой скорости и получили уравнения общего вида, позволяющие её рассчитать. Мы пришли к тому, что она естественным путем выводится из оператора поворота связанной с телом системы координат.
А что внутри этого оператора? Для случая декартовых координат легко получить матрицы поворота и легко обнаружить их свойства, связав с ними какой-нибудь способ описание ориентации тела, например углы Эйлера или Крылова. Или вектор и угол конечного поворота. Или кватернион. Но это для декартовых координат.
Начав говорить о тензорах мы отреклись от декартовых координат. Тем хороша тензорная запись, что она позволяет составить уравнения для любой удобной системы координат, не зацикливаясь на её свойствах. И проблема в том, что для, например косоугольных координат, матрицы поворота, даже для плоского случая, крайне сложны. Мне хватило проверки их вида для простого поворота в плоскости.
Так что задача этой статьи — не заглядывая внутрь тензора поворота исследовать его свойства и получить тензорное соотношение для его расчета. А раз задача поставлена, то начнем её решать.
1. Свойства тензора поворота системы координат
Для того чтобы вернуться к вопросам механики свободного твердого тела, необходимо понять, что представляет собой тензор поворота. Свойства тензора определяются набором его компонент и соотношением между ними. Так как тензор поворота есть тензор второго ранга и его компоненты представлены матрицей, то, не в ущерб общей тематике цикла, изложение этого параграфа буду вести, употребляя термин «матрица». Привычную «бесточечную» запись матричного произведения будем писать с точкой, так как в рамках алгебры тензоров мы имеем дело с комбинацией тензорного произведения со сверткой. Однако, тут тоже нужна оговорка — раскритиковав сам себя за некорректное употребление термина «свертка», я упустил тот момент, что под сверткой часто понимают и её комбинацию с тензорным умножением. При этом говорят, например, «свернем вектор с тензором Леви-Чивиты и получим…», имея в виду как раз операцию внутреннего произведения.
Итак, рассмотрим основные свойства матрицы поворота
- Преобразование поворота метрического тензора есть тождественное преобразование
- Определитель матрицы поворота по модулю равен единице
- Матрица обратного преобразования подобна транспонированной матрице прямого преобразования
- Если
, то матрица алгебраических дополнений и союзная матрица, построенные из
подобны этой и её транспонированной матрице, а преобразованием подобия является метрический тензор
Следствием данного свойства является равенство следов перечисленных матриц
- Если
, то собственные числа матрицы поворота по модулю равны единице и имеют вид
где
- Если
— собственный вектор матрицы поворота, соответствующий комплексному собственному числу, то справедливо соотношение
Следствие: действительная и мнимая части собственного вектора, соответствующего комплексному собственному числу, являются ортогональными векторами
где.
Доказательства свойств в основном тексте приводить не буду — статья и так обещает быть объемной. Эти доказательства не слишком сложны, но для интересующихся ими сделан нижеследующий спойлер.
Доказательство свойств 1 - 6 для пытливого и дотошного читателя
Свойства 1 и 3 мы доказали в предыдущей статье. Свойство 2 доказывается из свойства 1 тривиально, опираясь на свойства определителя матричного произведения

%5E2%20%3D%201)

Свойство 4 вытекает из аналитического способа вычисления обратной матрицы. , то
, то


где — союзная матрица (транспонированная матрица алгебраических дополнений). Транспонируя (1), пользуясь симметричностью метрического тензора, получаем
— союзная матрица (транспонированная матрица алгебраических дополнений). Транспонируя (1), пользуясь симметричностью метрического тензора, получаем
%5ET)
%5ET)

где — матрица, составленная из алгебраических дополнений матрицы поворота. Соотношения (1) и (2) — это соотношения подобия. Следы подобных матриц одинаковы
— матрица, составленная из алгебраических дополнений матрицы поворота. Соотношения (1) и (2) — это соотношения подобия. Следы подобных матриц одинаковы
%20%3D%20%5Cmathop%7B%5Crm%20tr%7D%5Cmathbf%7BB%7D)
Докажем свойство 5. Пусть — собственное число матрицы поворота, которому соответствует собственный вектор
— собственное число матрицы поворота, которому соответствует собственный вектор  . Тогда
. Тогда

Умножаем это выражение на матрицу обратного преобразования слева

с учетом свойства 3

Выполняем комплексное сопряжение, учитывая, что матрица поворота и метрический тензор имеют действительные компоненты и их сопряжение сводится к транспонированию
%5E%7B*%7D)
%5E%7BT%7D)

Последнее выражение умножаем справа на


Окончательно имеем уравнение
%5Cmathbf%7Bu%7D%5E%7B*%7D%20%5Ccdot%20%5Cmathbf%7Bg%7D%20%5Ccdot%20%5Cmathbf%7Bu%7D%20%3D%200)
которое справедливо лишь когда

то есть

Для вычисления собственных чисел составим характеристическое уравнение
%20%3D%200)
вычисляя определитель, приходим к общему виду этого уравнения (для матрицы размерности (3 х 3))
)
Вводим обозначение
)
Разлагаем (4) на множители
%5Cleft(%5Clambda%5E2%20%2B%20%5Clambda%20%2B%201%20%5Cright%20)%20-%20s%20%5C%2C%20%5Clambda%20%5Cleft(%5Clambda%20-%201%20%5Cright%20)%20%3D%200)
%5Cleft(%5Clambda%5E2%20-%20%5Clambda%20%5Cleft(s%20-%201%20%5Cright%20)%20%2B%201%20%5Cright%20)%20%3D%200)
откуда сразу получаем

Оставшуюся пару корней находим решая квадратное уравнение
%5E2%20-%201%7D)
Введем замену

которая правомерна, ибо, полагая корни, в общем случае комплексно-сопряженными, по теореме Виета имеем

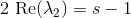
или, по абсолютному значению
%5Cright%7C%20%3D%20%5Cleft%7Cs-1%5Cright%7C)
Так как%5Cright%7C%20%5Cle%20%5Cleft%7C%5Clambda_2%5Cright%7C%20%3D%201)
то, очевидно

Производя замену, окончательно вычисляем

Доказательство свойства 6, будем проводить, опираясь на выражение

полученное при доказательстве равенства единице модуля собственного значения. Теперь, вместо комплексного сопряжения, транспонируем его, учитывая свойства операции транспонирования матричного умножения

Умножаем полученное выражение на справа
справа


Теперь умножим полученное уравнение на число комплексно-сопряженное собственному значению, учитывая что его модуль равен единице


Окончательно приходим к уравнению
%20%5C%2C%20%5Cmathbf%7Bu%7D%5ET%20%5Ccdot%20%5Cmathbf%7Bg%7D%20%5Ccdot%20%5Cmathbf%7Bu%7D%20%3D%200)
в котором скобка, в силу комплексности собственного числа нулю не равна, так как
)
Тогда справедливо

Следствие из данного свойства доказывается простым перемножением
%5ET%20%5Ccdot%20%5Cmathbf%7Bg%7D%20%5Ccdot%20%5Cleft(%5Cmathbf%7Bu%7D_%7B%5C%2Cr%7D%20%2B%20i%20%5C%2C%20%5Cmathbf%7Bu%7D_%7B%5C%2Ci%7D%20%5Cright%20)%20%3D%20%5Cleft(%5Cmathbf%7Bu%7D_%7B%5C%2Cr%7D%5ET%20%2B%20i%20%5C%2C%20%5Cmathbf%7Bu%7D_%7B%5C%2Ci%7D%5ET%20%5Cright%20)%20%5Ccdot%20%5Cmathbf%7Bg%7D%20%5Ccdot%20%5Cleft(%5Cmathbf%7Bu%7D_%7B%5C%2Cr%7D%20%2B%20i%20%5C%2C%20%5Cmathbf%7Bu%7D_%7B%5C%2Ci%7D%20%5Cright%20)%20%3D)

Приравниваем к нулю действительную и мнимые части


Из последних уравнений следует искомая ортогональность и равенство модулей и
и 
Свойство 4 вытекает из аналитического способа вычисления обратной матрицы.
где
где
Докажем свойство 5. Пусть
Умножаем это выражение на матрицу обратного преобразования слева
с учетом свойства 3
Выполняем комплексное сопряжение, учитывая, что матрица поворота и метрический тензор имеют действительные компоненты и их сопряжение сводится к транспонированию
Последнее выражение умножаем справа на
Окончательно имеем уравнение
которое справедливо лишь когда
то есть
Для вычисления собственных чисел составим характеристическое уравнение
вычисляя определитель, приходим к общему виду этого уравнения (для матрицы размерности (3 х 3))
Вводим обозначение
Разлагаем (4) на множители
откуда сразу получаем
Оставшуюся пару корней находим решая квадратное уравнение
Введем замену
которая правомерна, ибо, полагая корни, в общем случае комплексно-сопряженными, по теореме Виета имеем
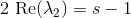
или, по абсолютному значению
Так как
то, очевидно
Производя замену, окончательно вычисляем
Доказательство свойства 6, будем проводить, опираясь на выражение
полученное при доказательстве равенства единице модуля собственного значения. Теперь, вместо комплексного сопряжения, транспонируем его, учитывая свойства операции транспонирования матричного умножения
Умножаем полученное выражение на
Теперь умножим полученное уравнение на число комплексно-сопряженное собственному значению, учитывая что его модуль равен единице
Окончательно приходим к уравнению
в котором скобка, в силу комплексности собственного числа нулю не равна, так как
Тогда справедливо
Следствие из данного свойства доказывается простым перемножением
Приравниваем к нулю действительную и мнимые части
Из последних уравнений следует искомая ортогональность и равенство модулей
Для чего нам знать о свойствах тензора поворота?
Во-первых, я полностью сформулировал их, для того, чтобы читатель мог увидеть, чем матрица поворота криволинейной системы координат отличается от матрицы поворота декартовой системы. Практически ни чем, свойства этих матриц схожи. Если в вышеприведенных выражениях положить матрицу метрического тензора единичной, то получаются свойство ортогональной матрицы поворота, почитать о которых можно, например у Д. Ю. Погорелова. Собственно данная книга сообщила мне, куда надо копать, чтобы рассмотреть задачу в общем виде.
Во-вторых, и это главное, мы докажем, что собственные векторы и собственные значения этих матриц имеют механический смысл. Для начала докажем лемму
Пусть— собственный вектор, соответствующий действительному собственному числу тензора поворота, а
— соответствует
, причем
. Пусть, так же, векторы
и
действительная и мнимая часть
. Тогда векторы
,
и
образуют тройку ортогональных векторов
Свойство 6 уже говорит нам об ортогональности
По определению собственных векторов
Умножим (3) слева на
Учитывая свойство 3 можно сказать, что
Кроме того, из (2) непосредственно следует
Учитывая (6) и (5) преобразуем (4)
Выражение в скобках — комплексное число, отличное от нуля. Значит верно утверждение (1) и рассматриваемые векторы образуют ортогональную тройку.
Доказанная нами лемма нужна для того чтобы показать — тензор поворота, рассматриваемый нами в произвольных координатах, удовлетворяет известной теореме Эйлера о конечном повороте.
2. Теорема Эйлера о конечном повороте
Исследовав тензор поворота мы поняли, что с этим тензором непосредственно связана ортогональная тройка векторов
Этот вектор остается неподвижным при повороте! А при повороте тела неподвижной остается… ось вращения. Значит вектор
Для любого тела, имеющего одну неподвижную току, и занимающего произвольное положение в пространстве, существует ось, проходящая через неподвижную точку, поворотом вокруг которой на конечный угол тело можно перевести в любое другое желаемое положение.
Тождество (7) дает нам подсказку о том где стоит искать эту ось вращения — она проходит через собственный вектор тензора поворота, соответствующий его действительному собственному числу. Проверим это, доказав теорему
Связанная с телом система координат может быть совмещена с базовой системой координат поворотом вокруг векторана угол
против часовой стрелки, если векторы
образуют правую тройку, и на угол
если эти векторы образуют левую тройку

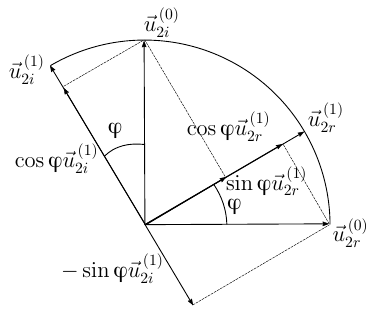
Рис 1. К доказательству теоремы о конечном повороте
Повернем связанную с телом систему координат на угол
Выражения (8) и (9) получены путем анализа конечного поворота. С другой стороны, из определения собственного вектора и свойств оператора поворота следует цепь преобразований
Приравнивая действительные и мнимые части (10), получаем
Сравнивая (8) и (11), (9) и (12) приходим к выводу, что применение оператора поворота к векторам приводит к их повороту вокруг оси
Надо сказать, наши результаты выглядят довольно эффектно — ведь не зная о внутренностях тензора поворота мы исследовали все (по крайней мере практически значимые его свойства). А нам не особенно интересны внутренности конкретных тензоров поворота, наша главная задача научится вычислять этот тензор, чтобы он обеспечивал поворот вокруг нужной нам оси на требуемый угол
3. Выражение тензора поворота через параметры конечного поворота. Формула Родрига
Рассмотрим конечный поворот произвольного вектора. В базовой системе координат его положение соответствует
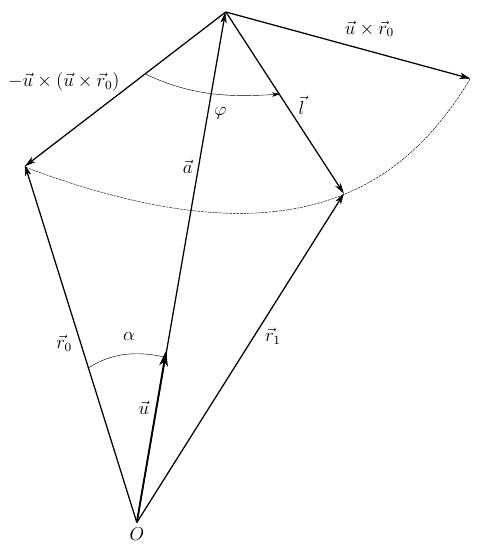
Рис. 2. Конечный поворот произвольного вектора
Из рисунка 2 очевидны векторное соотношения
где
Вектор
С другой стороны, ниже перечисленные векторы имеют одинаковый модуль
значит вектор
Теперь, выписанные векторные соотношения представим в тензорной компонентной форме
и введем два антисимметричных тензора
С учетом которых можно записать
Свертку тензоров (16) и (17) по общему индексу, выполним, расписав их через матрицы компонентов
Нетрудно заметить что (19) эквивалентно
Преобразуем (18) с учетом (20)
Из (21) получаем выражение для оператора поворота
где
– антисимметричный тензор ранга (0,2), порождаемый ортом оси поворота.
или, в бескомпонентной форме
Выражения (22) и (23) называются формулой поворота Родрига. Мы получили их для координатной системы с произвольной невырожденной метрикой.
Заключение
Всё вышеизложенное рассматривалось для одной единственной цели — получить выражение оператора поворота для произвольной системы координат. Это позволит нам выразить через (23) тензор и псевдовектор угловой скорости, а затем и углового ускорения. После этого мы выберем параметры, характеризующие ориентацию твердого тела в пространстве (это будут параметры Родрига-Гамильтона, да-да, мы поговорим о кватернионах) и запишем уравнения движения твердого тело в обобщенных координатах. По пути мы посмотрим на то, как тензоры облегчают получение уравнений, вывод которых традиционными способами занял бы уйму времени и сил, со множеством ошибок и умозрительных допущений.
Спасибо за внимание!
Продолжение следует…