Содержание
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
- Свойства тензора инерции твердого тела
- Зарисовка о гайке Джанибекова
- Математическое моделирование эффекта Джанибекова
Введение
В этой статье мы решим два вопроса — получим выражения для угловой скорости и углового ускорения через параметры Родрига-Гамильтона, о которых мы, подробнее чем планировалось, поговорили в прошлой статье. А заодно продемонстрируем, как можно использовать для этой цели открытую СКА Maxima, которая, как оказалось, неплохо справляется с тензорами, и при наличии определенных навыков может стать серьезным подспорьем для решения научных задач. Для меня Maxima — новый продукт, до этого я работал с Maple и совсем чуть-чуть с Mathematica. Поэтому, возможно, некоторые используемые мной приёмы могут показаться непрофессиональными.

СКА готова нам помочь и ждет разумной команды...
В прошлый раз мы остановились на том, что показали, как алгебру кватернионов можно использовать для представления преобразования поворота. Зная направление оси поворота, задаваемое ортом
и тогда, прямое преобразование поворота вектора
а обратное преобразование
Мы показали, что преобразования (2) и (3), проведенные над вектором непосредственно, дают формулу Родрига, описывающую конечный поворот. Теперь наша цель — связать параметры кватерниона поворота с тензором поворота и псевдовекторами угловой скорости и углового ускорения.
1. Тензор поворота в параметрах Родрига-Гамильтона
Нам уже хорошо знакомо выражение для тензора поворота
Введем кватернион, представив его векторную часть контравариантными компонентами
В данном случае, подстановку (5) в (4) можно выполнить вручную, ничего экстраординарного этот процесс не предполагает. Но мы выполним всё в Maxima, заодно подготовив некоторые исходные данные для дальнейшей работы. Настраиваем Maxima для работы с тензорами в трехмерном пространстве
/* Очищаем память */
kill(all);
/* Загружаем пакеты для работы с тензорами и генерации LaTeX вывода */
load(itensor);
load(tentex);
/* Даем имя метрическому тензору и задаем размерность пространства */
imetric(g);
idim(3);
Вводим выражение (4) тензора поворота
B:ishow(2*sin(phi/2)^2*u([],[m])*u([k],[]) +
(cos(phi/2)^2 - sin(phi/2)^2)*kdelta([k],[m]) +
2*sin(phi/2)*cos(phi/2)*g([],[m,i])*'levi_civita([i,j,k],[])*u([],[j]))$
Обратите внимание на ньюанс — мы перешли к половинным углам. Иначе, при попытке упрощения тригонометрии Maxima ничего не упростит, не помогает даже выставление флага
halfangles, который включает учет формул половинного аргумента. Это первый костыль, который мне пришлось применить. Возможно по незнанию.Задаем связь между параметрами конечного поворота и компонентами кватерниона
Lambda0:p0 = cos(phi/2);
Lambda:ishow(p([],[j]) = sin(phi/2)*u([],[j]))$
Здесь, для краткости (лень каждый раз вводить
lambda) компоненты кватерниона обозначены буквой pВыражаем орт оси поворота через векторную часть кватерниона
Solv1:ishow(solve(Lambda, u([],[j])))$
получая на выходе решение уравнение в виде массива выражений

В полученном выражении необходимо опустить индекс, так как тензор поворота содержит ковариантные компоненты орта поворота. Для этого сворачиваем полученное до этого выражение с метрическим тензором
u_k:ishow(contract(Solv1[1]*g([k,j],[])))$
Кроме того, заменим индекс j на m в ковариантных компонентах
um:ishow(subst(m, j, Solv1[1]))$
В итоге мы получим два выражения, готовых для подстановки в тензор поворота

Теперь мы можем подставить компоненты орта оси поворота в выражение для тензора поворота. Функция постановки
subst() в данном случае принимает два аргумента — выражение, которое нужно подставить в выражение, идущее вторым аргументом. При этом в преобразуемом выражении ищется левая часть первого аргумента и заменяется на его правую частьB_1:ishow(subst(u_k, B))$
B_1:ishow(subst(um, B_1))$
B_1:ishow(subst(Solv1[1], B_1))$
На выходе имеем
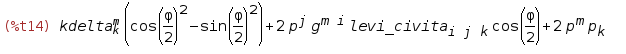
Отлично, теперь в тензоре поворота фигурируют компоненты векторной части кватерниона. Теперь упростим тригонометрию
B_2:ishow(trigsimp(B_1))$
Функция
trigsim() упрощает тригонометрические выражения. При этом, как написано в документации, учитывает по умолчанию основное тригонометрическое тождество и четность/нечетность тригонометрических функций. Однако, то ли загрузка пакета тензорной алгебры так влияет, данная функция спотыкается на упрощении дробей, содержащих функции одинарного и половинного аргументов, даже при взведенном флаге, о котором упоминалось выше. Тем не менее мы провели подготовительную работу и на выходе получим упрощенную формулу
Осталось заменить квадраты косинуса и синуса половинного угла поворота на скалярный параметр кватерниона, для чего выполним подстановку и упрощение в виде раскрытия скобок
B_3:ishow(subst(p0,rhs(Lambda0), B_2))$
B_3:ishow(expand(subst(1-p0^2,sin(phi/2)^2, B_3)))$
И, чтобы полюбоваться на результат, выведем его в LaTeX
tentex(B_3);
К выведенному коду я добавил лишь левую часть
Видно, что Maxima генерирует LaTeX-нотацию, весьма близкую к естественной математической записи, чего не скажешь о Maple, который готовит монструозный код, содержащий все условности, принятые им при выводе читабельных формул. Слагаемые, содержащие дельту Кронекера сгруппируем и вынесем общим множитель за скобки уже самостоятельно. Ну и вернем на место «лямбду»
Нами получено выражение тензора поворота через параметры Родрига-Гамильтона. От этого тензора можно перейти к любым другим параметрам, описывающим ориентацию твердого тела в пространстве.
Разминку можно считать оконченной. Впереди нас ждет более серьезная работа
2. Псевдовектор угловой скорости в параметрах Родрига-Гамильтона
Введем в Maxima уже известное нам выражение для псевдовектора угловой скорости. В естественной форме оно выглядит так
А в Maxima пойдет с заменой функций одинарных углов на эквивалентные функции половинных
Omega:ishow(2*sin(phi/2)^2*'levi_civita([],[i,m,r])*u([i],[])*diff(u([m],[]),t) +
diff(u([],[r]),t)*2*sin(phi/2)*cos(phi/2) + u([],[r])*diff(phi, t))$
Напомню, что тензор Леви-Чивиты, особенно если планируется упрощать выражение с применением его свойств, лучше вводить с подавлением вычисления. Иначе Maxima превратит его в обобщенную дельту Кронекера, а это в наши планы не входит. Для подавления вычисления ставим апостроф перед именем функции, задающей этот тензор.
Опускаем индексы и переименовываем индексы орта поворота, в соответствии с обозначением индексов в тензоре угловой скорости
u_i:ishow(contract(Solv1[1]*g([i,j],[])))$
u_m:ishow(subst(m, i, u_i))$
ur:ishow(subst(r, j, Solv1[1]))$
Получаем выражения, которые будем использовать в подстановках

Нам будут необходимы производные от орта оси поворота и от угла поворота. Необходимо получить их выраженными через параметры кватерниона
/* Дифференцируем ковектор орта оси поворота по времени */
du_mdt:ishow(diff(u_m, t))$
/* Дифференцируем по времени скалярный параметр кватерниона */
dLambda0dt:diff(Lambda0, t);
/* Выражаем производную угла поворота */
Solv2:solve(dLambda0dt, diff(phi,t));
Maxima выполнит все операции вполне корректно

Но вот тут нас подстерегает ещё один нюанс. Нам надо убрать производные из полученных выражений. То есть убрать совсем. Потому что Maxima, при упрощении выражений, не совсем адекватно на них реагирует. Например, если одна и та же производная стоит в выражении как коэффициент перед синусом в квадрате и перед косинусом в квадрате одного и того же угла, то при упрощении тригонометрии Maxima не видит в упор основного тригонометрического тождества. А если производную заменить на обычное выражение — легко схлопывает тождество в единицу. То же касается и тензорных преобразований — на лицо нежелание опускать индексы и сворачиваться с тензором Леви-Чивиты если один из тензоров, участвующих в операции представлен производной по времени от другого тензора. Прямых указаний на решение проблемы я пока не встретил, хотя ищу их, а пока применим костыль номер два — введем замены. Для начала в выражении угловой скорости заменим производную скалярного параметра кватерниона
dphidt:subst(v0, diff(p0,t), Solv2[1]);
Выполняем прямую подстановку — первый аргумент функции
subst() это то на что, надо заменить выражение, преданное вторым аргументом, в выражении, стоящем в третьем аргументе. Результат
нас устраивает. Теперь подставляем эту угловую скорость в выражение для производной ковектора орта оси поворота
du_mdt:ishow(subst(dphidt, du_mdt))$
и выполняем замену производных от остальных параметров кватерниона
du_mdt:ishow(subst(v([m],[]), diff(p([m],[]),t), du_mdt))$
ну и поднимаем индексы, для получения производной от контравариантных компонент орта
durdt:ishow(diff(u([],[r]),t) = contract(expand(rhs(du_mdt)*g([],[r,m]))))$
На выходе имеем полный набор выражений для выполнения подстановки

Что же, выполняем их, раскрывая по пути скобки, заставляя Maxima сокращать по возможности дроби
Omega_1:ishow(subst(dphidt, Omega))$
Omega_1:ishow(expand(subst(du_mdt, Omega_1)))$
Omega_1:ishow(expand(subst(durdt, Omega_1)))$
Omega_1:ishow(expand(subst(u_i, Omega_1)))$
Omega_1:ishow(expand(subst(ur, Omega_1)))$
Результат уже вполне себе приличный
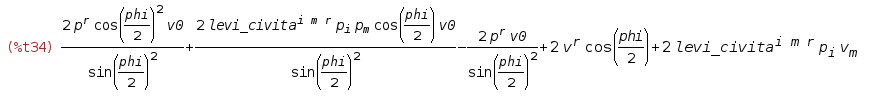
но во втором слагаемом маячит векторное произведения векторной части кватерниона самой на себя, равная нулю. Чтобы СКА убрала её воспользуемся заклинанием
Omega_2:ishow(canform(contract(expand(applyb1(Omega_1, lc_l, lc_u)))))$
Подробности конструирования этой команды описаны мной здесь. Напомню лишь смысл — упростить тензорное выражение по правилам работы со свертками тензора Леви-Чивиты. Заклинание убирает нулевой член

Дело за малым — причесать тригонометрию
Omega_3:ishow(trigsimp(Omega_2))$
и заменить оставшийся косинус на скалярный параметр кватерниона
Omega_3:ishow(subst(lhs(Lambda0), rhs(Lambda0) , Omega_3))$
В результате имеем довольно компактное выражение
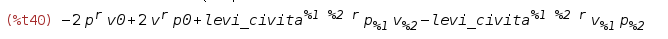
Выведем его в LaTeX
tentex(Omega_3);
Погоду портят нумерованные функцией
canform() немые индексы, но тут уже мы ручками поставим нужные нам имена индексов и заодно вернем на место производные от параметров Родрига-ГамильтонаВыражение (7) и есть долгожданное выражение угловой скорости через параметры Родрига-Гамильтона. Как видно, оно гораздо компактнее исходного выражения, записанного в параметрах конечного поворота. Но это не единственная положительная черта. Другая приятная особенность откроется нам, когда мы получим
3. Угловое ускорение в параметрах Родрига-Гамильтона
Существует два пути получения углового ускорения. Первый путь, самый простой, до которого я, почему-то не сразу дошел, просто продифференцировать (7) по времени. Это легко и быстро делается вручную. Второй путь, по которому я честно прополз, получить формулу в Maxima, упростив известное нам выражение углового ускорения через параметры конечного поворота
Продемонстрирую оба пути, только длинный путь уберу под спойлер, чтобы мой уважаемый читатель не потерял за деревьями леса.
Итак, возьмем производную по времени от (7)
Первое слагаемое — ноль, подобные приводятся вплоть до взаимного уничтожения членов, и итоге, без особого труда, получаем
А длинный путь к получению (8) можно посмотреть тут
Итак, введем в Maxima угловое ускорение в параметрах конечного поворота, помня о половинных углах
Теперь нам понадобятся вторые производные. Дифференцируем угол поворота
и подставляем в него уже обработанное нами ранее выражение для первой производной угла
Снова избавляемся от первых и вторых производных параметров, вводя соответствующие замены
имея на выходе выражение, пригодное для подстановки

Прежде чем дифференцировать тензоры, добавим в список функций времени введенные нами замены для первых производных, иначе получим нули, которых на деле нет
Вычисляем вторую производную от орта оси поворота, производим необходимые замены, поднимаем индексы для получения необходимых нам выражений ковариантных компонент с нужными индексами
На выходе имеем вторые производные ковариантных и контравариантных компонент, пригодные для подстановки

Выполняем серию подстановок — заменяем производные угла и орта, а так же компоненты самого орта на полученные выше, и ранее, при вычислении угловой скорости, выражения
Полученный «крокодил» колоссален

Но мы укротим его заклинанием упрощения сверток с тензором Леви-Чивиты
и получим менее страшное, но ещё сложное выражение

Теперь упростим тригонометрию, и заменим косинус половинного угла на скалярный параметр кватерниона, а так же выведем LaTeX
И вместо «крокодила» имеем вполне приличную формулу, в которой угадывается результат (8)

И если мы её причешем, внеся соответствующие поправки в обозначения и приведя подобные до конца, то

(8) мы и получаем. Только гораздо дольше. Но зато проверили правильность исходных формул.
epsilon:ishow(2*sin(phi/2)^2*'levi_civita([],[i,m,r])*u([i],[])*diff(u([m],[]),t,2) +
diff(phi,t)*2*cos(phi/2)^2*diff(u([],[r]),t) +
diff(phi,t)*2*sin(phi/2)*cos(phi/2)*'levi_civita([],[i,m,r])*u([i],[])*diff(u([m],[]),t) +
diff(u([],[r]),t,2)*2*sin(phi/2)*cos(phi/2) + u([],[r])*diff(phi,t,2))$
Теперь нам понадобятся вторые производные. Дифференцируем угол поворота
d2phidt2:diff(Solv2[1],t);
и подставляем в него уже обработанное нами ранее выражение для первой производной угла
d2phidt2:diff(Solv2[1],t);
Снова избавляемся от первых и вторых производных параметров, вводя соответствующие замены
d2phidt2:subst(v0, diff(p0,t), d2phidt2);
d2phidt2:subst(a0, diff(p0,t,2), d2phidt2);
имея на выходе выражение, пригодное для подстановки

Прежде чем дифференцировать тензоры, добавим в список функций времени введенные нами замены для первых производных, иначе получим нули, которых на деле нет
depends([v0, v],t);
Вычисляем вторую производную от орта оси поворота, производим необходимые замены, поднимаем индексы для получения необходимых нам выражений ковариантных компонент с нужными индексами
d2u_mdt2:ishow(diff(du_mdt, t))$
d2u_mdt2:ishow(subst(dphidt, d2u_mdt2))$
d2u_mdt2:ishow(subst(a0, diff(v0,t), d2u_mdt2))$
d2u_mdt2:ishow(subst(a([m],[]), diff(v([m],[]),t), d2u_mdt2))$
d2u_mdt2:ishow(subst(v([m],[]), diff(p([m],[]),t), d2u_mdt2))$
d2urdt2:ishow(diff(u([],[r]),t,2) = contract(expand(rhs(d2u_mdt2)*g([],[r,m]))))$
На выходе имеем вторые производные ковариантных и контравариантных компонент, пригодные для подстановки

Выполняем серию подстановок — заменяем производные угла и орта, а так же компоненты самого орта на полученные выше, и ранее, при вычислении угловой скорости, выражения
epsilon_1:ishow(subst(dphidt, epsilon))$
epsilon_1:ishow(expand(subst(durdt, epsilon_1)))$
epsilon_1:ishow(expand(subst(du_mdt, epsilon_1)))$
epsilon_1:ishow(expand(subst(d2phidt2, epsilon_1)))$
epsilon_1:ishow(expand(subst(d2u_mdt2, epsilon_1)))$
epsilon_1:ishow(expand(subst(d2urdt2, epsilon_1)))$
epsilon_1:ishow(expand(subst(ur, epsilon_1)))$
epsilon_1:ishow(expand(subst(u_i, epsilon_1)))$
Полученный «крокодил» колоссален

Но мы укротим его заклинанием упрощения сверток с тензором Леви-Чивиты
epsilon_2:ishow(canform(contract(expand(applyb1(epsilon_1, lc_l, lc_u)))))$
и получим менее страшное, но ещё сложное выражение

Теперь упростим тригонометрию, и заменим косинус половинного угла на скалярный параметр кватерниона, а так же выведем LaTeX
epsilon_3:ishow(trigsimp(epsilon_2))$
epsilon_3:ishow(subst(lhs(Lambda0), rhs(Lambda0) , epsilon_3))$
tentex(epsilon_3);
И вместо «крокодила» имеем вполне приличную формулу, в которой угадывается результат (8)
И если мы её причешем, внеся соответствующие поправки в обозначения и приведя подобные до конца, то
(8) мы и получаем. Только гораздо дольше. Но зато проверили правильность исходных формул.
Внезапно, мы наблюдаем полную аналогию с (7), только вместо первых производных здесь стоят вторые производные. Коэффициенты при производных одинаковы, что означает, что угловая скорость и угловое ускорение получаются из соответствующих производных параметров Родрига-Гамильтона умножением на одну и ту же матрицу (3 x 4). Это, между прочим и определило широкую применимость кватернионного подхода при моделировании движения космических аппаратов, и прочих объектов, совершающих свободное вращение в пространстве.
Заключение
Статья вышла с уклоном на приемы работы с тензорными библиотеками Maxima. Могу сделать вывод, что, даже при описанных допущениях, упрощать тензорные выражения в ней достаточно удобно.
Ну и, наконец, мы получили выражения угловой скорости и углового ускорения через удобные для моделирования параметры ориентации Родрига-Гамильтона. И убедились в том, что формулы (7) и (8) их выражающие не только компактны, но и красивы, в том смысле, что используют одно и то же линейное преобразование параметров к кватерниона к компонентам векторов угловых скорости и ускорения. Такой подход серьезно упрощает организацию моделирующих программ, в чем мы ещё, я надеюсь, убедимся.
На сегодняшний день мы вплотную подошли к рассмотрению динамики свободного твёрдого тела с применением тензорного аппарата. На счёт следующей статьи у меня есть интересная идея, которую я постараюсь реализовать и подготовить качественный материал.
Благодарю за внимание!
Продолжение следует...