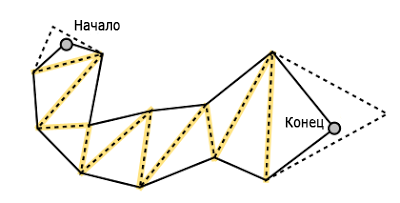
Алгоритм воронки — это простой алгоритм поиска наипростейшего пути, проходящего через «порталы». Наиболее подробное описание можно найти по ссылке Efficient Triangulation-Based Pathfinding (2)
Здесь же этот алгоритм будет реализован до одури просто. Вместо использования очередей и прочих очешуительных вещей, наша простейшая реализация перезапускает цикл каждый раз, когда обнаруживает очередной угол. Это значит, что некоторые порталы будут опрашиваться таки чаще, чем должны были бы, тем не менее, делая реализацию всяко проще.
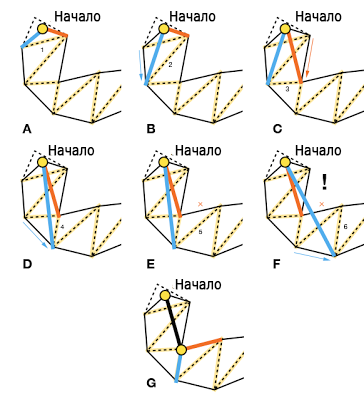
Полотно выше показывает 6 этапов этого алгоритма. На проверке каждой грани портала (муравьи на чём-то жёлтом), выполняются следующие действия:
- Проверяем находятся ли внутри текущего тоннеля точки слева и справа. Если «да», то мы идём дальше, ничего не предпринимая (A-D).
- Если новая левая точка снаружи тоннеля, тоннель не обновлён (E-F)
- Если новая левая точка находится за правой гранью тоннеля (F), мы добавляем правую точку тоннеля в качестве угла пути и устанавливаем и устанавливаем эту (левую) точку в качестве стартовой точки и перезапускаем алгоритм (G).
Эти правила применяются и для левой грани.
Как видно из примера выше, некоторые грани перепроверяются несколько раз, но все эти вычисления настолько просты, что оверхед пренебрежительно мал, давая на выходе простую и практичную реализацию.
Плохо скрытый код
Массив portals содержит в себе все сегменты порталов пути, который требуется упростить, первую точку грани слева и первую точку грани справа. Первая правая и первая левая точки — это наша стартовая точка, и последние левые и правые точки это наша конечная точка. Т.е. примерно так: inline float triarea2(const float* a, const float* b, const float* c)
{
const float ax = b[0] - a[0];
const float ay = b[1] - a[1];
const float bx = c[0] - a[0];
const float by = c[1] - a[1];
return bx*ay - ax*by;
}
inline bool vequal(const float* a, const float* b)
{
static const float eq = 0.001f*0.001f;
return vdistsqr(a, b) < eq;
}
int stringPull(const float* portals, int nportals,
float* pts, const int maxPts)
{
// Поиск прямого пути.
int npts = 0;
// Начальное сканирование
float portalApex[2], portalLeft[2], portalRight[2];
int apexIndex = 0, leftIndex = 0, rightIndex = 0;
vcpy(portalApex, &portals[0]);
vcpy(portalLeft, &portals[0]);
vcpy(portalRight, &portals[2]);
// Установка стартовой точки.
vcpy(&pts[npts*2], portalApex);
npts++;
for (int i = 1; i < nportals && npts < maxPts; ++i)
{
const float* left = &portals[i*4+0];
const float* right = &portals[i*4+2];
// Обновление правой вершины.
if (triarea2(portalApex, portalRight, right) <= 0.0f)
{
if (vequal(portalApex, portalRight) || triarea2(portalApex, portalLeft, right) > 0.0f)
{
// Сжимаем тоннель.
vcpy(portalRight, right);
rightIndex = i;
}
else
{
// Правая вершина находится за левой, вставляем ЛЕВУЮ точку в путь, ставим в качестве стартовой и перезапускаем
vcpy(&pts[npts*2], portalLeft);
npts++;
// устанавливаем стартовую точку.
vcpy(portalApex, portalLeft);
apexIndex = leftIndex;
// сброс портала
vcpy(portalLeft, portalApex);
vcpy(portalRight, portalApex);
leftIndex = apexIndex;
rightIndex = apexIndex;
// перезапуск
i = apexIndex;
continue;
}
}
// обновляем левую вершину.
if (triarea2(portalApex, portalLeft, left) >= 0.0f)
{
if (vequal(portalApex, portalLeft) || triarea2(portalApex, portalRight, left) < 0.0f)
{
// сжимаем тоннель.
vcpy(portalLeft, left);
leftIndex = i;
}
else
{
// Левая точка за правой, вставляем ПРАВУЮ точку в путь, ставим в качестве стартовой и перезапускаем.
vcpy(&pts[npts*2], portalRight);
npts++;
// устанавливаем стартовую точку
vcpy(portalApex, portalRight);
apexIndex = rightIndex;
// сброс портала
vcpy(portalLeft, portalApex);
vcpy(portalRight, portalApex);
leftIndex = apexIndex;
rightIndex = apexIndex;
// перезапуск
i = apexIndex;
continue;
}
}
}
// добавляем последнюю точку в путь.
if (npts < maxPts)
{
vcpy(&pts[npts*2], &portals[(nportals-1)*4+0]);
npts++;
}
return npts;
}
// Стартовый портал
vcpy(&portals[nportals*4+0], startPos);
vcpy(&portals[nportals*4+2], startPos);
nportals++;
// Портал между полигонами навмеша
for (int i = 0; i < path->npolys-1; ++i)
{
getPortalPoints(mesh, path->poly[i], path->poly[i+1], &portals[nportals*4+0], &portals[nportals*4+2]);
nportals++;
}
// Финальный портал
vcpy(&portals[nportals*4+0], endPos);
vcpy(&portals[nportals*4+2], endPos);
nportals++;
Каплей мёда в бочке мёда является то, что этот алгоритм может быть реализован в контексте любого формата навигации. Сетка, соединённые квадраты, квадродерево, путевые точки (вейпоинты) или навмеш — безразлично, главное чтобы вы могли предоставить список сегментов, которые являют собой порталы из одной ноды в другую.
Алгоритм так-же неплохо совмещается со стирингом. Вы вольны посчитать желаемую скорость передвижения, исходя из следующих поворотов. Это настолько быстро, что вы можете считать её (скорость) на каждой итерации перед применением шага стиринга.
p.s. Ознакомиться с более полным вариантом крайне рекомендуется — хотя-бы по-диагонали (от переводчика).