 Исследуя одну задачу оптимизации, столкнулся с проблемой симметричности конфигураций при прямом переборе вариантов. Схожая проблема возникает в некоторых решениях задачи о восьми ферзях. Исследуя центральную симметрию прямоугольной сетки, я обнаружил
Исследуя одну задачу оптимизации, столкнулся с проблемой симметричности конфигураций при прямом переборе вариантов. Схожая проблема возникает в некоторых решениях задачи о восьми ферзях. Исследуя центральную симметрию прямоугольной сетки, я обнаружил Немного о симметрии
Центральная симметрия или симметрия с центром в точке — это преобразование пространства, переводящее точку X в точку X’ так, что центр симметрии будет центром отрезка XX’. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре.
Если же мы говорим о центральной симметрии сетки, состоящей из клеток, то тут речь будет идти не о точках, а о клетках сетки. Например, после центрально-симметричного преобразования шахматной доски клетка A1 станет на место H8, A2 — на H7, а B1 — на G8.
В этой статье мы будем использовать прямоугольную сетку. Как и прямоугольник, такая сетка имеет две оси симметрии и один центр, но сконцентрируемся только на центральной симметрии.
Суть вопроса
Имеется сетка размером 3 на 6 клеток. Также в наличии список из 14 компонент, любой из которых может быть поставлен в любую клетку, причем возможны повторы. Количество вариантов заполнения такой сетки с повторами равно 1418, естественно было бы неплохо их уменьшить в два раза, отбросив варианты заполнения, которые являются центрально-симметричными к уже проверенным. Для простоты вывода пусть компонентами будут числами от 0 до 13 включительно. Список из 18 компонент генерируется функцией product из пакета itertools (если быть точным, то функция возвращает кортеж-итератор, который, подобно одометру, на каждой итерации меняет правостоящий элемент). Этим списком по столбикам и заполняется сетка.
Примеры нулевой, первой, второй и 178-ой конфигурации сетки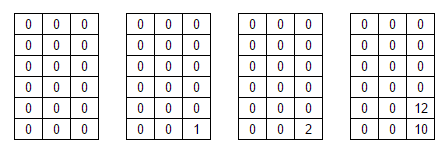

Задача: Исключить варианты заполнения сетки, центрально-симметричные уже проверенным вариантам.
Реализация
Пронумеруем клетки по столбикам, начиная с левого верхнего угла, от 0 до 17. Попытаемся для каждой конфигурации найти номер симметричной ей относительно центра. Нумерация конфигураций, как обычно, с нуля.
Конфигурация 0 (все ячейки с нулями) очевидно симметрична сама себе: 0 -> 0.
Конфигурация 1. Клетка 17 получает 1, остальные с нулями. Симметричной к ней будет конфигурация, в которой в клетке 0 стоит «1», остальные с нулями. Клетка 17 пройдет 14 своих значений (от 0 до 13) за первые 14 итераций. Клетка 16 тоже за 14, но на каждую ее конфигурацию приходится 14 итераций клетки 17, т.е. за 142, и т.д. Следовательно, клетка 0 наберет 1 на 1417 итерации.
Конфигурация 2. Клетка №17 получает 2, остальные с нулями. Симметричной к ней будет конфигурация 2⋅1417, в которой в клетке 0 стоит 2, остальные нули.
Конфигурация 3 -> Конфигурация 3⋅1417
Конфигурация 4 -> Конфигурация 4⋅1417 и т.д. до 13 -> 13⋅1417.
Следуя этой логике, стоит записать номер варианта, симметричного первому, как 1⋅1417, а симметричного нулевому — как 0⋅1417.
Уже имеем некоторый список номеров конфигураций, симметричных друг другу:
- 0 и 0⋅1417
- 1 и 1⋅1417
- 2 и 2⋅1417
и т.д. до 13.
Конфигурация 14. 1 находится в предпоследней клетке, остальные нули. Симметричной к ней является 1⋅1416.
Конфигурация 15. Единицы в двух последних клетка, остальные нули. Симметричная к ней, когда 1 в первых двух ячейках, остальные нули. 1 становится в ячейку №0 на итерации 1417, а еще через 1416 1 появится и в клетке №1, следовательно искомая конфигурация будет под номером 1416 + 1417.
Конфигурация 16. Элемент «А» в ячейке №16, «B» — в ячейке №17. Симметричная к ней, очевидно 1416 + 2⋅1417.
…
Конфигурация 27 -> 1⋅1416 + 13⋅1417.
Конфигурация 28 -> 2⋅1416.
Конфигурация 29 -> 2⋅1416 + 1417.
Эта история продолжается до итерации 195, которая симметрична 13⋅1416 + 13⋅1417. В итерации 196 в ячейку №15 ставится 1, остальные пусты. Симметрична к ней итерация 1415.
В итерации 197 единица ставится еще и в ячейку №17, потому симметрична к ней — 1415 + 1417, и т.д.
Общий закон симметрии конфигураций сетки будет таким:
Тут мне показалась знакомой формула слева. Это формула перевода числа из системы счисления с произвольным основанием в десятичную. И, соответственно
Нетрудно заметить, что в правой части записано число из левой части в обратном порядке — если в левой части мы «пишем» число справа налево, то в левой — теми же цифрами, но слева направо. Проще говоря, число справа — это «перевертыш» числа слева, причем оба записаны в системе счисления с основанием 14 и имеют длину 18.
Критерий и алгоритм валидации
Если номер конфигурации длинной в количество клеток и записанный в системе счисления с основанием, равным количеству элементов, меньше собственного номера-«перевертыша», то конфигурация симметричная данной еще не встречалась. Если же они (номера) равны, то имеем дело с палиндромом, который встречается только один раз и, следовательно, подлежит проверке.
Сам алгоритм валидации такой:
- Перевести номер конфигурации в систему счисления с основанием, равным количеству элементов
- Записать число-«перевертыш» длиной 18
- Если «перевертыш» больше номера конфигурации, то симуляции этой конфигурации и симметричной к ней еще не проводились; если нет, то проводилась симуляция конфигурации, симметричной этой, следовательно — пропустить.
Или в виде кода
def validate(number, radix, length):
fingers = '0123456789abcdefghijklmnopqrstuvwxyz'
n = number
# перевод в систему счисления с основанием radix без разворота
turn = ''
while n > 0:
turn += fingers[n % radix]
n = n // radix
# добавим недостающие нули до нужной длинны
turn += '0' * (length - len(turn))
return number <= int(turn, radix)
Заключение
Очевидно, этот алгоритм применим не только для определения центральной симметрии двумерной сетки, но и сетки в произвольном измерении, потому что любую такую конфигурацию возможно свести к списку, или списком заполнить сетку, например, построчно.
Сам алгоритм довольно тяжелый, что вызывает вопрос о применимости его на практике. Но в случае, когда проверка каждой конфигурации стоит еще больше вычислительных ресурсов, то, возможно, стоит его использовать.