Библиотека RandLib позволяет работать с более чем 50 известными распределениями, непрерывными, дискретными, двумерными, циклическими и даже одним сингулярным. Если нужно какое-нибудь распределение, то вводим его имя и добавляем суффикс Rand. Заинтересовались?
Генераторы случайных величин
Если мы хотим сгенерировать миллион случайных величин из нормального распределения, используя стандартную библиотеку шаблонов C++, мы напишем что-нибудь вроде
std::random_device rd;
std::mt19937 gen(rd());
std::normal_distribution<> X(0, 1);
std::vector<double> data(1e6);
for (double &var : data)
var = X(gen);
Шесть интуитивно не очень понятных строчек. RandLib позволяет их количество сократить вдвое.
NormalRand X(0, 1);
std::vector<double> data(1e6);
X.Sample(data);
Если нужна лишь одна случайная стандартная нормально распределённая величина, то это можно сделать в одну строчку
double var = NormalRand::StandardVariate();
Как можно заметить, RandLib избавляет пользователя от двух вещей: выбора базового генератора (функции, возвращающей целое число от 0 до некого RAND_MAX) и выбора стартовой позиции для случайной последовательности (функция srand()). Сделано это во имя удобства, так как многим пользователям этот выбор скорее всего ни к чему. В подавляющем большинстве случаев случайные величины генерируются не непосредственно через базовый генератор, а через случайную величину U, распределенную равномерно от 0 до 1, которая уже зависит от этого базового генератора. Для того, чтобы изменить способ генерации U, нужно воспользоваться следующими директивами:
#define UNIDBLRAND // генератор дает большее разрешение за счет комбинации двух случайных чисел
#define JLKISS64RAND // генератор дает большее разрешение за счет генерации 64-битных целых чисел
#define UNICLOSEDRAND // U может вернуть 0 или 1
#define UNIHALFCLOSEDRAND // U может вернуть 0, но никогда не вернет 1
По умолчанию U не возвращает ни 0, ни 1.
Скорость генерации
В последующей таблице предоставлено сравнение времени на генерацию одной случайной величины в микросекундах.
Характеристики системы
Ubuntu 16.04 LTS
Процессор: Intel Core i7-4710MQ CPU @ 2.50GHz × 8
Тип ОС: 64-разрядная
Процессор: Intel Core i7-4710MQ CPU @ 2.50GHz × 8
Тип ОС: 64-разрядная
| Распределение | STL | RandLib |
|---|---|---|
| 0.017 μs | 0.006 μs | |
| 0.075 μs | 0.018 μs | |
| 0.109 μs | 0.016 μs | |
| 0.122 μs | 0.024 μs | |
| 0.158 μs | 0.101 μs | |
| 0.108 μs | 0.019 μs |
Больше сравнений
| Гамма-распределение: | ||
|---|---|---|
| 0.207 μs | 0.09 μs | |
| 0.161 μs | 0.016 μs | |
| 0.159 μs | 0.032 μs | |
| 0.159 μs | 0.03 μs | |
| 0.159 μs | 0.082 μs | |
| Распределение Стьюдента: | ||
| 0.248 μs | 0.107 μs | |
| 0.262 μs | 0.024 μs | |
| 0.33 μs | 0.107 μs | |
| 0.236 μs | 0.039 μs | |
| 0.233 μs | 0.108 μs | |
| Распределение Фишера: | ||
| 0.361 μs | 0.099 μs | |
| 0.319 μs | 0.013 μs | |
| 0.314 μs | 0.027 μs | |
| 0.331 μs | 0.169 μs | |
| 0.333 μs | 0.177 μs | |
| Биномиальное распределение: | ||
| 0.655 μs | 0.033 μs | |
| 0.444 μs | 0.093 μs | |
| 0.873 μs | 0.197 μs | |
| Распределение Пуассона: | ||
| 0.048 μs | 0.015 μs | |
| 0.446 μs | 0.105 μs | |
| Отрицательное биномиальное распределение: | ||
| 0.297 μs | 0.019 μs | |
| 0.587 μs | 0.257 μs | |
| 1.017 μs | 0.108 μs |
Как можно увидеть, RandLib иногда в 1.5 раза быстрее, чем STL, иногда в 2, иногда в 10, но никогда медленнее. Примеры реализованных в RandLib алгоритмов можно посмотреть здесь и здесь.
Функции распределения, моменты и прочие свойства
Помимо генераторов RandLib предоставляет возможность рассчитать функции вероятности для любого из данных распределений. Например, чтобы узнать вероятность того, что случайная величина с распределением Пуассона с параметром a примет значение k нужно вызвать функцию P.
int a = 5, k = 1;
PoissonRand X(a);
X.P(k); // 0.0336897
Так сложилось, что именно заглавная буква P обозначает функцию, возвращающую вероятность принятия какого-либо значения для дискретного распределения. У непрерывных распределений эта вероятность равна нулю почти всюду, поэтому вместо этого рассматривается плотность, которая обозначается буквой f. Для того, чтобы рассчитать функцию распределения, как для непрерывных, так и для дискретных распределений нужно вызвать функцию F:
double x = 0;
NormalRand X(0, 1);
X.f(x); // 0.398942
X.F(x); // 0
Иногда нужно посчитать функцию 1-F(x), где F(x) принимает очень маленькие значения. В таком случае, чтобы не потерять точность следует вызывать функцию S(x).
Если же нужно посчитать вероятности для целого набора значений, то для этого нужно вызвать функции:
//x и y - std::vector
X.CumulativeDistributionFunction(x, y); // y = F(x)
X.SurvivalFunction(x, y); // y = S(x)
X.ProbabilityDensityFunction(x, y) // y = f(x) - для непрерывных
X.ProbabilityMassFunction(x, y) // y = P(x) - для дискретных
Квантиль — это функция от p, возвращающая x, такой что p = F(x). Соответствующие реализации есть также в каждом конечном классе RandLib, соответствующем одномерному распределению:
X.Quantile(p); // возвращает x = F^(-1)(p)
X.Quantile1m(p); // возвращает x = S^(-1)(p)
X.QuantileFunction(x, y) // y = F^(-1)(x)
X.QuantileFunction1m(x, y) // y = S^(-1)(x)
Иногда вместо функций f(x) или P(k) нужно достать соответствующие им логарифмы. В таком случае лучше всего воспользоваться следующими функциями:
X.logf(k); // возвращает x = log(f(k))
X.logP(k); // возвращает x = log(P(k))
X.LogProbabilityDensityFunction(x, y) // y = logf(x) - для непрерывных
X.LogProbabilityMassFunction(x, y) // y = logP(x) - для дискретных
Также RandLib предоставляет возможность рассчитать характеристическую функцию:
X.CF(t); // возвращает комплексное значение \phi(t)
X.CharacteristicFunction(x, y) // y = \phi(x)
Кроме того, можно легко достать первые четыре момента или математическое ожидание, дисперсию, коэффициенты асимметрии и эксцесса. Кроме того, медиану (F^(-1)(0.5)) и моду (точку, где f или P принимает наибольшее значение).
LogNormalRand X(1, 1);
std::cout << " Mean = " << X.Mean()
<< " and Variance = " << X.Variance()
<< "\n Median = " << X.Median()
<< " and Mode = " << X.Mode()
<< "\n Skewness = " << X.Skewness()
<< " and Excess kurtosis = " << X.ExcessKurtosis();
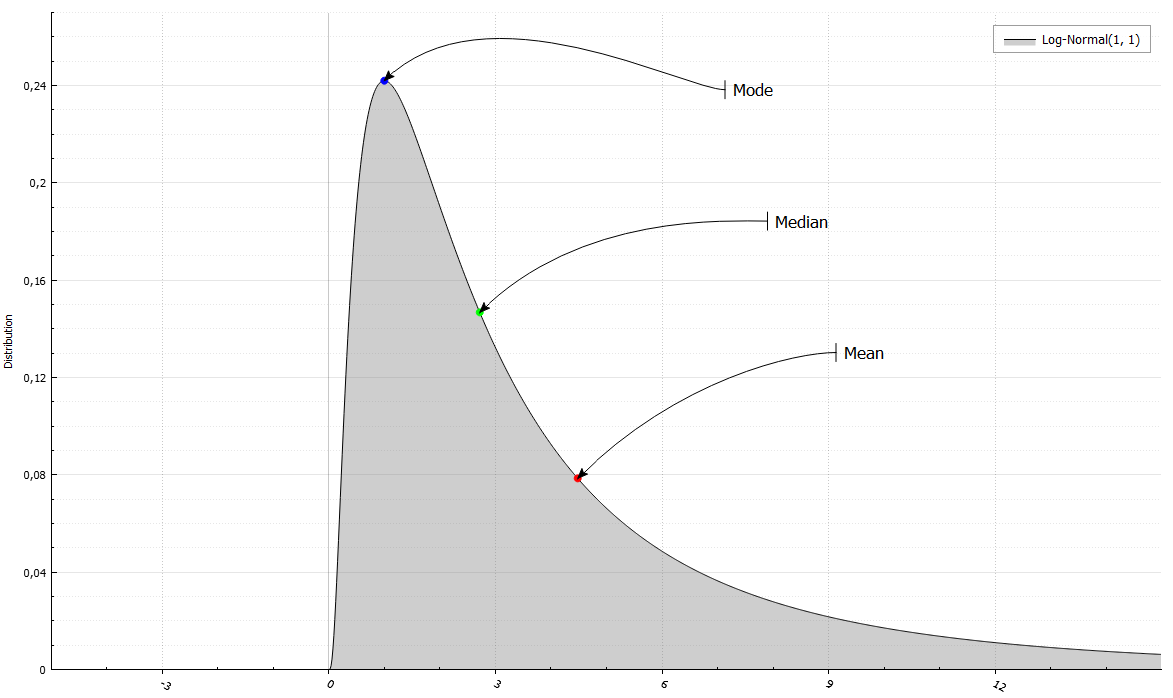
Mean = 4.48169 and Variance = 34.5126
Median = 2.71828 and Mode = 1
Skewness = 6.18488 and Excess Kurtosis = 110.936
Оценки параметров и статистические тесты
От теории вероятностей к статистике. Для некоторых (пока не для всех) классов есть функция Fit, которая задает параметры, соответствующие некоторой оценке. Рассмотрим на примере нормального распределения:
using std::cout;
NormalRand X(0, 1);
std::vector<double> data(10);
X.Sample(data);
cout << "True distribution: " << X.Name() << "\n";
cout << "Sample: ";
for (double var : data)
cout << var << " ";
Мы сгенерировали 10 элементов из стандартного нормального распределения. На выходе должны получить что-нибудь вроде:
True distribution: Normal(0, 1)
Sample: -0.328154 0.709122 -0.607214 1.11472 -1.23726 -0.123584 0.59374 -1.20573 -0.397376 -1.63173
Функция Fit в данном случае задаст параметры, соответствующие оценке максимального-правдоподобия:
X.Fit(data);
cout << "Maximum-likelihood estimator: " << X.Name(); // Normal(-0.3113, 0.7425)
Как известно, максимальное правдоподобие для дисперсии нормального распределения даёт смещенную оценку. Поэтому в функции Fit есть дополнительные параметр unbiased (по умолчанию false), которым можно настраивать смещенность / несмещенность оценки.
X.Fit(data, true);
cout << "UMVU estimator: " << X.Name(); // Normal(-0.3113, 0.825)
Для любителей Байесовской идеологии также есть и Байесовская оценка. Структура RandLib позволяет очень удобно оперировать априорным и апостериорным распределениями:
NormalInverseGammaRand prior(0, 1, 1, 1);
NormalInverseGammaRand posterior = X.FitBayes(data, prior);
cout << "Bayesian estimator: " << X.Name(); // Normal(-0.2830, 0.9513)
cout << "(Posterior distribution: " << posterior.Name() << ")"; // Normal-Inverse-Gamma(-0.2830, 11, 6, 4.756)
Тесты
Как узнать, что генераторы, как и функции распределения возвращают правильные значения? Ответ: сравнить одни с другими. Для непрерывных распределений реализована функция, проводящая тест Колмогорова-Смирнова на принадлежность данной выборки соответствующему распределению. На вход функция KolmogorovSmirnovTest принимает порядковую статистику и уровень \alpha, а на выход возвращает true, если выборка соответствует распределению. Дискретным распределениям соответствует функция PearsonChiSquaredTest.
Заключение
Данная статья специально написана для части хабрасообщества, интересующейся подобным и способной оценить. Разбирайтесь, ковыряйтесь, пользуйтесь на здоровье. Основные плюсы:
- Бесплатность
- Открытый исходный код
- Скорость работы
- Удобство пользования (моё субъективное мнение)
- Отсутствие зависимостей (да-да, не нужно ничего)
Ссылка на релиз.