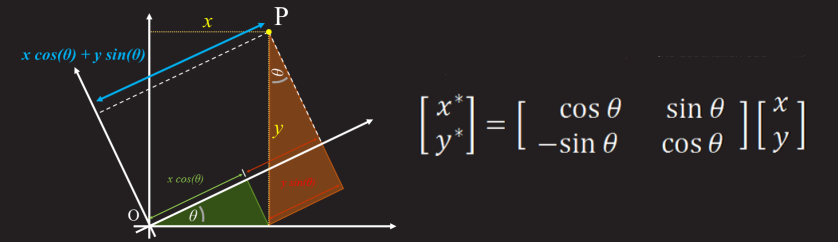
Пол года назад я наткнулся в сети вот на это видео.
Первой мыслью было то, что это очень круто и у меня такое никогда не получится повторить. Шло время, читались статьи, изучались методы и я искал примеры реализации подобного, но к моему огорчению, в сети ничего конкретного не находилось. Наткнувшись однажды на вычисления тригонометрических функций с использованием алгоритмов CORDIC, я решил попробовать создать свою собственную вращалку изображения на ПЛИС.
CORDIC
Итак, CORDIC — это аббревиатура от COordinate Rotation DIgital Computer.
Это мощный инструмент для вычисления гиперболических и тригонометрических функций. Большинство алгоритмов CORDIC работают методом последовательного приближения и не очень сложны в реализации как на языках программирования высокого уровня, так и на HDL. Я не стану заострять внимание на математике метода, читатель может ознакомиться с ним в сети или по ссылкам ниже.
В свободном доступе мне попалась вот эта реализация алгоритма CORDIC на языке verilog. Данное ядро работает в 2-х режимах: Rotate и Vector. Для наших целей подходит режим Rotate. Он позволяет вычислять значения функций sin и cos от заданного угла в радианах или градусах. Библиотеку можно сконфигурить как в конвейерном, так и в комбинационном варианте. Для наших целей подходит конвейер, у него самое большое Fmax. Он выдаст значения синуса и косинуса с задержкой в 16 тактов.
В RTL Viewer-e модуль CORDIC отображается состоящим из 16 однотипных блоков:

Каждый из которых принимает на вход данные с предыдущего и выходами подключен ко входам следующего. Выглядит он так:

Ядро библиотеки работает только в первом квадранте, а это значит что оставшиеся три нам придётся вычислять самим вычитая pi/2 и меняя знак.
Выбранный мной подход не является очень правильным т.к. качество вращаемого изображения оставляет желать лучшего. Это происходит по причине расчета координат на-лету, без применения дополнительной буферизации данных и последовательного вычисления координат за несколько проходов, как это делается в Shear.
Первой инстанцией нашего вращателя является блок расчёта квадранта и угла поворота. Угол поворота инкрементируется каждый новый кадр на 1 градус. По достижению угла 90 градусов, квадрант меняется на следующий по очереди, а угол либо сбрасывается в ноль, либо декрементируется на 1 градус каждый новый кадр.
Выглядит это так:
always @(posedge clk) begin
if (!nRst) begin
cordic_angle <= 17'd0;
cordic_quadrant <= 2'd0;
rotator_state <= 2'd0;
end else begin
if (frame_changed) begin
case (rotator_state)
2'd0: begin
if (cordic_angle[15:8] == 8'd89) begin
cordic_quadrant <= cordic_quadrant + 1'b1;
rotator_state <= 2'd1;
end else
cordic_angle[15:8] <= cordic_angle[15:8] + 1'b1;
end
2'd1: begin
if (cordic_angle[15:8] == 8'd1) begin
cordic_quadrant <= cordic_quadrant + 1'b1;
rotator_state <= 2'd0;
end else
cordic_angle[15:8] <= cordic_angle[15:8] - 1'b1;
end
default: rotator_state <= 2'd0;
endcase
end
end
end
Далее значение угла подаётся на модуль CORDIC, который и вычисляет нам значения sin и cos.
cordic CORDIC(
.clk(clk),
.rst(~nRst),
.x_i(17'd19896),
.y_i(16'd0),
.theta_i(cordic_angle),
.x_o(COS),
.y_o(SIN),
.theta_o(),
.valid_in(),
.valid_out()
);
Далее не сложно догадаться, что расчёт координат каждого последующего пикселя будет производиться по формуле:
x’ = cos(angle) * x — sin(angle) * y;
y’ = sin(angle) * x + cos(angle) * y;

Если оставить всё в таком виде, то вращение будет с центром в начале координат. Такое вращение нас не устраивает, нам нужно чтобы картинка вращалась вокруг своей оси с центром в середине изображения. Для этого нам надо вести вычисления относительно центра изображения.
parameter PRECISION = 15;
parameter OUTPUT = 12;
parameter INPUT = 12;
parameter OUT_SIZE = PRECISION + OUTPUT;
parameter BUS_MSB = OUT_SIZE + 2;
wire [15:0] res_x = RES_X - 1'b1;
wire [15:0] res_y = RES_Y - 1'b1;
assign dx = {1'b0, RES_X[11:1]};
assign dy = {1'b0, RES_Y[11:1]};
always @(posedge clk) begin
delta_x <= dx << PRECISION;
delta_y <= dy << PRECISION;
еnd
Далее вычисляем значения cos(angle) * x, sin(angle) * x, cos(angle) * y, sin(angle) * y.
Можно вычислять и так:
always @(posedge clk) begin
mult_xcos <= (xi - dx) * COS;
mult_xsin <= (xi - dx) * SIN;
mult_ycos <= (yi - dy) * COS;
mult_ysin <= (yi - dy) * SIN;
end
Но я решил использовать мегафункции lpm_mult. Их использование значительно повышает Fmax.
reg signed [BUS_MSB: 0] tmp_x, tmp_y, mult_xsin, mult_xcos, mult_ysin, mult_ycos;
reg signed [BUS_MSB: 0] delta_x = 0, delta_y = 0;
wire signed [11:0] dx, dy;
reg signed [BUS_MSB: 0] mxsin, mxcos, mysin, mycos;
reg signed [11:0] ddx, ddy;
always @(posedge clk) begin
ddx <= xi - dx;
ddy <= yi - dy;
end
wire signed [BUS_MSB-1: 0] mult_xcos1;
wire signed [BUS_MSB-1: 0] mult_xsin1;
wire signed [BUS_MSB-1: 0] mult_ycos1;
wire signed [BUS_MSB-1: 0] mult_ysin1;
lpm_mult M1(.clock(clk), .dataa(COS), .datab(ddx), .result(mult_xcos1));
defparam M1.lpm_widtha = 17;
defparam M1.lpm_widthb = 12;
defparam M1.lpm_pipeline = 1;
defparam M1.lpm_representation = "SIGNED";
lpm_mult M2(.clock(clk), .dataa(SIN), .datab(ddx), .result(mult_xsin1));
defparam M2.lpm_widtha = 17;
defparam M2.lpm_widthb = 12;
defparam M2.lpm_pipeline = 1;
defparam M2.lpm_representation = "SIGNED";
lpm_mult M3(.clock(clk), .dataa(COS), .datab(ddy), .result(mult_ycos1));
defparam M3.lpm_widtha = 17;
defparam M3.lpm_widthb = 12;
defparam M3.lpm_pipeline = 1;
defparam M3.lpm_representation = "SIGNED";
lpm_mult M4(.clock(clk), .dataa(SIN), .datab(ddy), .result(mult_ysin1));
defparam M4.lpm_widtha = 17;
defparam M4.lpm_widthb = 12;
defparam M4.lpm_pipeline = 1;
defparam M4.lpm_representation = "SIGNED";
После умножения получаем произведения, знак которых нам необходимо менять в каждом следующем квадранте:
always @(posedge clk) begin
mxcos <= mult_xcos1;
mxsin <= mult_xsin1;
mycos <= mult_ycos1;
mysin <= mult_ysin1;
case (cordic_quadrant)
2'd0: begin
mxsin <= -mult_xsin1;
end
2'd1: begin
mxcos <= -mult_xcos1;
mxsin <= -mult_xsin1;
mycos <= -mult_ycos1;
end
2'd2: begin
mxcos <= -mult_xcos1;
mysin <= -mult_ysin1;
mycos <= -mult_ycos1;
end
2'd3: begin
mysin <= -mult_ysin1;
end
endcase
end
Теперь дело осталось за малым — вычислить сами координаты пикселя:
/*
I II III IV
+ + + - - - - -
+ - + + + - - +
*/
always @(posedge clk) begin
tmp_x <= delta_x + mxcos + mysin;
tmp_y <= delta_y + mycos + mxsin;
end
wire [15:0] xo = tmp_x[BUS_MSB] ? 12'd0: tmp_x[OUT_SIZE-1:PRECISION];
wire [15:0] yo = tmp_y[BUS_MSB] ? 12'd0: tmp_y[OUT_SIZE-1:PRECISION];
Отсекаем пиксели, выходящие за границы изображения:
wire [11:0] xo_t = (xo[11:0] > res_x[11:0]) ? 12'd0 : xo[11:0];
wire [11:0] yo_t = (yo[11:0] > res_y[11:0]) ? 12'd0 : yo[11:0];
И его адрес в памяти:
//addr_out <= yo[11:0] * RES_X + xo[11:0];
И снова используем lpm_mult:
reg [11:0] xo_r, yo_r;
always @(posedge clk) begin
xo_r <= xo_t;
yo_r <= yo_t;
end
wire [28:0] result;
lpm_mult M5(.clock(clk), .dataa(RES_X[11:0]), .datab(yo_r[11:0]), .result(result));
defparam M5.lpm_widtha = 12;
defparam M5.lpm_widthb = 12;
defparam M5.lpm_pipeline = 1;
defparam M5.lpm_representation = "UNSIGNED";
always @(posedge clk) addr_out <= result[22:0] + xo_r[11:0];
Вот, собственно, и всё!
Проблемы метода
Как я уже упоминал выше, данный подход имеет много недостатков. Из-за погрешности вычисления в выходной картинке появляются дыры, чем больше угол поворота, тем больше дыр. Это ещё происходит и по тому, что размеры новой картинки больше чем у оригинала. Этот эффект завётся aliasing и существуют методы борьбы с ним, например, медианный фильтр, расмотренный в моей предыдущей статье.
Перед каждым последующим кадром не мешало бы почистить память от предыдущего кадра, чтобы новое изображение получалось на чистом фоне, но это занимает время и придётся пропускать один кадр.
Единственным достоинством метода является простота реализации и скорость обработки т.к. координаты вычисляются на-лету.
Вот что из этого получилось
Ссылки по теме
→ CORDIC на русском
→ CORDIC for dummies
→ CORDIC FAQ
Архив проекта в Квартусе
→ Ссылка на яндекс диск.