Наткнулась на эту задачу совершенно случайно. У меня знакомая через год после окончания магистратуры снова решила учиться и начала готовиться к поступлению. А значит что-то нужно просто повторить и вспомнить, ну и разобраться с чем-то новым. Вот сидела она над какой-то задачей, я проходила мимо. Задача показалась весьма простой (школьного уровня), но надо немного подумать.
Итак, рассматриваемая здесь задача звучит так: даны угол и точка внутри него. Через эту точку провести отрезки, имеющие концы на сторонах угла, так, чтобы полученный треугольник имел наименьший периметр.

Задачка является частью доказательства задачи Фаньяно.
Первые мысли, которые приходят в голову, это, наверное, построить перпендикуляры (как кратчайшее расстояние до сторон). Отображаем точку симметрично относительно
симметрично относительно  и
и  (получаем точки
(получаем точки  и
и  ).
).

У некоторых сразу же может возникнуть искушение соединить точки пересечения перпендикуляров и сторон угла . После чего появляется ложное впечатления «я сделяль», и кажется, что
. После чего появляется ложное впечатления «я сделяль», и кажется, что  — это тот самый треугольник.
— это тот самый треугольник.
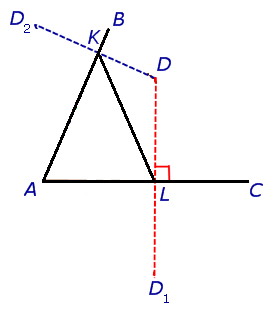
Всё не так. Тот факт, что две стороны треугольника — кратчайшие (перпендикуляры до прямой), еще не делает периметр треугольника минимальным.
На самом деле поиск треугольника с наименьшим периметром использует утверждение: кратчайшее расстояние между двумя точками – прямая. Дополнительные построения должны привести к тому, чтобы все длины сторон искомого треугольника оказались на прямой. Соединяем точки и
и  . Точки пересечения прямой
. Точки пересечения прямой  со сторонами угла и есть оставшиеся искомые вершины треугольника.
со сторонами угла и есть оставшиеся искомые вершины треугольника.
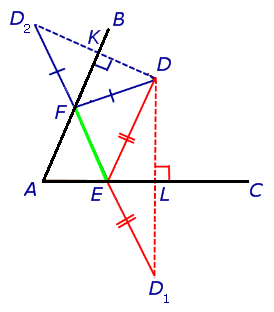
 и
и  являются медианами и высотами(точка
являются медианами и высотами(точка  симметрично отображена относительно сторон угла) треугольников
симметрично отображена относительно сторон угла) треугольников  и
и  соответственно, значит треугольники
соответственно, значит треугольники  и
и  — равнобедренные. Видно, что периметр треугольника
— равнобедренные. Видно, что периметр треугольника  равен длине отрезка
равен длине отрезка  . Треугольник с меньшим периметром найден.
. Треугольник с меньшим периметром найден.
Возьмем какие-нибудь другие точки( и
и  ) на сторонах угла.
) на сторонах угла.
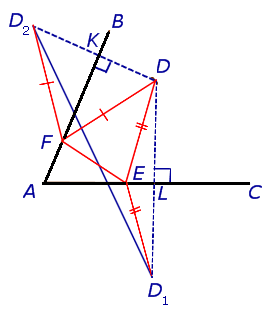
Периметр этого треугольника оказывается больше, чем длина отрезка
оказывается больше, чем длина отрезка  .
.
Вот и все. Удачи всем поступающим!
Итак, рассматриваемая здесь задача звучит так: даны угол и точка внутри него. Через эту точку провести отрезки, имеющие концы на сторонах угла, так, чтобы полученный треугольник имел наименьший периметр.

Задачка является частью доказательства задачи Фаньяно.
Сама задача Фаньяно звучит следующим образом:
Рассматриваются всевозможные треугольники  , вершины
, вершины  ,
,  и
и  которых лежат на сторонах
которых лежат на сторонах  ,
,  и
и  остроугольного треугольника
остроугольного треугольника  соответственно. Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника
соответственно. Доказать, что из всех треугольников DEF наименьшим периметром обладает ортоцентрический треугольник треугольника  .
.
Ортоцентрический треугольник
Ортоцентрическим треугольником (ортотреугольником) называют треугольник, вершинами которого служат основания высот исходного треугольника.
Первые мысли, которые приходят в голову, это, наверное, построить перпендикуляры (как кратчайшее расстояние до сторон). Отображаем точку

У некоторых сразу же может возникнуть искушение соединить точки пересечения перпендикуляров и сторон угла

Всё не так. Тот факт, что две стороны треугольника — кратчайшие (перпендикуляры до прямой), еще не делает периметр треугольника минимальным.
На самом деле поиск треугольника с наименьшим периметром использует утверждение: кратчайшее расстояние между двумя точками – прямая. Дополнительные построения должны привести к тому, чтобы все длины сторон искомого треугольника оказались на прямой. Соединяем точки

Возьмем какие-нибудь другие точки(

Периметр этого треугольника
Вот и все. Удачи всем поступающим!