Особенность координатных систем на точечном базисе (ди- и би-координат) состоит в том, что их можно использовать как в обычном геометрическом пространстве, так и в пространстве графа.
Мерность пространства графа определяется количеством его связанных вершин (будем считать, что все вершины графа связаны — однокомпонентный граф). Базис пространства задается как подмножество вершин графа с известными дистанциями между ними (метрикой). Подмножество может включать в себя как все вершины графа, так и только часть (подграф). В последнем случае мерность базиса меньше, чем мерность общего пространства графа.
Необходимо разобраться, что представляют собой элементы и векторы на графе. Граф — это набор связанных элементов (узлов). Узлы графа определяют его множество потенциальных базовых элементов, а связи — метрику, расстояние между базовыми элементами.
В качестве базиса для определения системы координат на графе могут быть выбраны не все узлы графа, а только его часть — базисный подграф. В этом случае общее пространство графа можно поделить на два подпространства — базисное и вне базисное (внешнее).
Узлы, вошедшие в базис графа, называются базисными. Все остальные элементы пространства задаются относительно его базовых узлов через барицентрические координаты (веса базовых вершин).
В общем случае элемент может либо принадлежать пространству базиса, либо лежать за его пределами. Элементы вне базиса будем называть внешними. Поскольку внешний элемент имеет отличную от нуля дистанцию до базисного пространства, то каждый внешний элемент — это узел графа, не вошедший в его базис. То есть внешние элементы явно заданы в структуре графа.
Элементы, принадлежащие пространству базиса, никак не проявляются в структуре, — виртуальные элементы (кроме собственно явно заданных вершин базиса). Норма виртуальных элементов равна нулю — это просто нормированный к единице вектор потенциалов на вершинах базиса. Примером виртуального элемента пространства базиса служит ортоцентр базиса.
Если граф представляет собой электрическую цепь, то элементом является совокупность потенциалов на узлах сети. Лапласианом электрической цепи является матрица, состоящая из проводимостей ребер. Умножение данной матрицы на электрические потенциалы узлов дает ток в узлах. Соответственно, потенциалы в узлах являются дистанционными координатами
, а суммарный ток узла — барицентрическими: 
. Преобразование координат просто отражает закон Ома:
В отличие от привычного восприятия пространства, в котором элементы — это нечто материальное, а их компоненты — виртуальны (веса, дистанции, проекции), в пространстве графа ситуация обратная. Компоненты элемента (потенциалы и токи в узлах) материальны, а положение элемента в пространстве как раз виртуально и определяется совокупностью значений компонент.
Задачу построения системы координат (СК) на графе можно сформулировать следующим образом.
Требуется определить координаты внешних вершин относительно базиса. Система координат должна позволять определять дистанции между всеми (любыми) вершинами графа.
Уточним, что приведена лишь одна из возможных формулировок задачи построения СК. Комбинации известных параметров и тех, что требуется определить, могут варьироваться.
Обозначим множество базовых вершин графа индексом
(anchor-якорь), а множество остальных вершин индексом 
. Объединение данных множеств дает все вершины графа. Считаем узлы графа связанными с остальными хотя бы одной связью.
Общий дистанционный метрический тензор (ДМТ) графа
можно разбить на 4 матрицы:
— дистанционный метрический тензор подграфа;
— матрица ди-координат внешних вершин в базисе . В данной матрице координаты вершины — это столбец матрицы, в транспонированной 
— строка.
— матрица скалярных произведений между вершинами графа, не входящих в базис.
По условиям задачи известным является только грамиан подграфа. Матрицы и — это то, что надо определить на основании данных о структуре графа.
Подобным же образом (на 4 подматрицы) можно разбить лапласиан графа
. В отличие от грамиана лапласиан графа здесь минорный — данные об ортоцентре графа отсутствуют.
— матрица связей (смежности) между внешними вершинами графа и его базисом .
— минор лапласиана, связи внешних вершин. На диагонали данной матрицы находятся значения общей проводимости узла (суммарный вес его ребер), остальные элементы — величина связи узлов между собой. Данная матрица обычно обратима. Ее обращение называется фундаментальной матрицей:
Термин «фундаментальная» взят из теории марковских цепей с поглощением. В таких цепях роль базовых играют узлы, из которых нет возврата (поглощающие). Пример использования данной матрицы приводился в статье о способе ранжирования объектов по степени их удаленности от заданных.
Предполагается, что одна из матриц (минор лапласиана или фундаментальная матрица 
) известны. Согласно (4.2) можно выразить одну из другой.
Грамиан и лапласиан графа взаимно обратны.
Для нахождения тождеств, связывающих между собой перечисленные выше матрицы, надо блочные матрицы (4.1.1) и (4.1.2) подставить в (4.3) (лапласиан предварительно окаймить условными параметрами ортоцентра). В итоге получаем следующие соотношения.
Связь лапласовского
и дистанционного метрических тензоров базиса подграфа:
(4.4.1) позволяет вычислить один тензор на основании другого. Если базис задан в виде связей, то для определения лапласиана базиса
можно использовать следующее тождество:
Здесь
— минор исходного лапласиана на базисных вершинах. — лапласиан, подматрица ЛМТ базиса. На основании данного лапласиана можно найти грамиан подграфа .
Если известна матрица связей между внешними узлами графа и его базисом
, а также фундаментальная матрица , то можно рассчитать барицентрические координаты узлов:
Матрицу барицентрических координат
называют также матрицей влияния. Действительно, ее значения отражают влияние базовых вершин на остальные (в задаче Дирихле — влияние значений граничных узлов на внешние).
Би- и ди-координаты узлов взаимны. Выражаются через метрический тензор базиса:
Ди-координаты включают в себя единицу и значения скалярных произведений элементов с базисом:![$Dm_{ta}=[1_t; D_{ta}]$](https://habrastorage.org/getpro/habr/formulas/c02/551/359/c025513599b3e999ff521d15bf26e294.svg)
.
Би-координаты состоят из скалярной компоненты (орбитали) и барицентрических координат:
![$Bm^{a}_{t}=[W_t; B^{a}_{t}]$](https://habrastorage.org/getpro/habr/formulas/9c8/301/295/9c8301295e10abca744d6d3f090d7bf0.svg)
Если известны детерминанты фундаментальной матрицы и ЛМТ базиса, то можно вычислить общий скалярный потенциал лапласиана графа:
Матрица скалярных произведений внешних вершин
в базисе подграфа представляет собой билинейную форму, выражается через би- или ди-координаты вершин:
Очевидно, что значения матрицы будут в общем случае отличаться от значений скалярных произведений вершин в исходном графе . Разница между ними выражается фундаментальное матрицей:
Формула (4.5) может быть использована для вычисления истинного скалярного произведения между вершинами (элементами), если известно скалярное произведение элементов в базисе подграфа и фундаментальная матрица .
В исходном графе нормы вершин равны нулю. Соответственно, скалярное произведение может быть выражено через квадрат расстояния между вершинами 
: 
. Тогда (4.5) можно представить в виде:
С данным выражением мы уже встречались во 2-й части при определении скалярного произведения элементов — (2.6). Сравнивая выражения видим, что значения фундаментальной матрицы можно выразить через скалярное произведение вершин относительно базиса:
Штрихами отмечены проекции вершин на базовое пространство.
— это скалярное произведение пар 
и 
.
Через
обозначено скалярное произведение нормалей вершин 
к пространству .
Нормаль задается как направление из элемента на его проекцию в пространстве базиса. Это близко к определению скалярного произведения координат элементов в обычных системах координат (на векторном базисе), только вместо начала координат здесь указывается пространство.
Если какая-либо из вершин принадлежит базисному пространству, то ее скалярное произведение относительно базиса с любой другой вершиной равно нулю. Таким образом, если один из элементов фундаментальной матрицы равен нулю, то нулевыми будут также вся строка и столбец матрицы.
Если элементы
и 
совпадают, то значение фундаментальной матрицы равно дистанции от элемента до базового пространства или согласно (2.5) отрицательной норме элемента:
— значения диагональных элементов фундаментальной матрицы.
Если вершины не принадлежат базовому пространству (принадлежат надпространству), то возможно две ситуации:
1. Вершины принадлежат одному и тому же (над)пространству. В этом случае вершины и их проекции на базовое пространство лежат в одной плоскости.
2. Вершины принадлежат разным (над)пространствам (показано на рисунке выше).
В первой ситуации направление нормалей
и 
коллинеарно, поэтому скалярное произведение совпадает с произведением расстояний от вершин до базового пространства:
Знак квадратного корня положителен, если вершины находятся по одну сторону пространства (нормали направлены в одну сторону) и отрицателен в обратном случае. Данная формула уже приводилась во 2-й статье серии — (2.7). Формула (4.6.3) описывает частный (хотя и важный) случай.
Для построения системы координат необходимо определить скалярную компоненту би-координат — то, что называется орбиталью элемента. Без данной компоненты дистанции в графе могут быть получены лишь в рамках базового пространства.
Про определении би-координат была получена формула, связывающая орбиталь элемента и его проекции на пространство базиса с нормой элемента — (2.9.1):
Орбиталь проекции элемента можно вычислить через билинейную форму (2.9.2), поскольку нам известна как грамиан базиса
, так и барицентрические координаты элементов (4.4.3). Значения норм элементов согласно (4.6.2) можно взять из диагональных элементов фундаментальной матрицы. Собирая все вместе, получаем выражение для матрицы взаимных орбиталей:
Диагональные значения данной матрицы
— это орбитали вершин.
Таким образом би-координаты внешних вершин определены. На основании би-координат можно вычислить ди-координаты по формуле (4.4.4), получить матрицу взаимных норм (4.4.2).
Задача построения системы координат выполнена.
Если базис содержит небольшое количество вершин, то часть формул обращения (4.4) может быть выражена в явном виде. Здесь рассмотрим базисы из одной и двух вершин.
Достаточно тривиален и поэтому не очень интересен. Дистанционный метрический тензор базиса не включает ни одной дистанции:
Все барицентрические координаты вершин относительно базиса равны 1 (поскольку всего одна компонента). Фундаментальная матрица совпадает с матрицей скалярных произведений пар, где первым элементом каждой пары является как раз вершина базиса. В 3-й части было показано, что дистанционную матрицу на основании такой матрицы можно получить через преобразование дистанции:
Такой базис имеет прикладное значение. Например, в рассмотренной нами ранее задаче электрометрии узлы, к которым прикладывается внешнее напряжение, — это и есть 2-вершинный базис.
Обозначим дистанцию между базовыми вершинами
и 
как 
. Напомним, что в электрической цепи дистанция эквивалентна сопротивлению между узлами. Тогда дистанционный метрический тензор базиса имеет вид:
Детерминант ДМТ:
. Лапласовский тензор (ЛМТ) получаем обращением дистанционного (4.4.1):
Ди-координаты вершин графа будут иметь три компоненты: скалярная (1), скалярные произведения
относительно базовой вершины и скалярные произведения 
относительно базовой вершины :
![$Dm=[1; d_A, d_B] \quad(4.11.1)$](https://habrastorage.org/getpro/habr/formulas/d56/f5a/ef4/d56f5aef4be9d16c990383530028676a.svg)
Би-координаты также имеют три компоненты. Скалярная компонента — это (геометрическая) орбиталь вершины.
![$Bm=[w; B]=[w; b_A, b_B] \quad(4.11.2)$](https://habrastorage.org/getpro/habr/formulas/809/951/9f3/8099519f307a41a1ad419468067522ac.svg)
Подставляя (4.11.1) в (4.4.5) и учитывая (3.8), получаем выражения для компонент би-координат вершины P:
![$Bm_P=[-g^P_{AB}/2; g^B_{AP}/r, g^A_{BP}/r] \quad(4.12)$](https://habrastorage.org/getpro/habr/formulas/503/fe0/3af/503fe03afb1ac455b883702ec4dd3953.svg)
Здесь через
обозначено скалярное произведение пар, начало которых находится в вершине 
, а концы — в элементах 
и 
.
Можно убедиться, что сумма барицентрических компонент равна 1, как и должно быть:
.
Барицентрическая часть координат в (4.12) представляет собой матрицу влияния — передает влияние базовых вершин на внешние. Если, например, на базовых вершинах заданы значения потенциалов
, то потенциалы остальных вершин 
определяются произведением заданных потенциалов на матрицу влияния:
Пусть вектор заданных потенциалов имеет вид![$U_a=[U_A, 0]$](https://habrastorage.org/getpro/habr/formulas/61c/48a/d80/61c48ad80c67f2cca1d51e202f9581ab.svg)
. Тогда разность потенциалов между элементами P и Q графа будет равна:
При выводе использовано тождество (3.9.4) для разности скалярных произведений смежных пар.
— это величина входящего потока, определяется уравнением 
.
Формула (4.15) в явном виде выражает связь разностей потенциалов на вершинах графа со скалярным произведением, на что было указано в предыдущей статье.
Подведем итоги. В данной части показано, как задать на графе систему координат. Приведены основные тождества, ключевыми из которых на наш взгляд являются (4.5) и (4.5.1).
Из обязательной программы осталось рассмотреть преобразование координат (смену базиса), чем и займемся в следующей статье.
Оглавление
Что такое пространство графа
Мерность пространства и мерность базиса
Мерность пространства графа определяется количеством его связанных вершин (будем считать, что все вершины графа связаны — однокомпонентный граф). Базис пространства задается как подмножество вершин графа с известными дистанциями между ними (метрикой). Подмножество может включать в себя как все вершины графа, так и только часть (подграф). В последнем случае мерность базиса меньше, чем мерность общего пространства графа.
Элементы в пространстве графа
Необходимо разобраться, что представляют собой элементы и векторы на графе. Граф — это набор связанных элементов (узлов). Узлы графа определяют его множество потенциальных базовых элементов, а связи — метрику, расстояние между базовыми элементами.
В качестве базиса для определения системы координат на графе могут быть выбраны не все узлы графа, а только его часть — базисный подграф. В этом случае общее пространство графа можно поделить на два подпространства — базисное и вне базисное (внешнее).
Узлы, вошедшие в базис графа, называются базисными. Все остальные элементы пространства задаются относительно его базовых узлов через барицентрические координаты (веса базовых вершин).
В общем случае элемент может либо принадлежать пространству базиса, либо лежать за его пределами. Элементы вне базиса будем называть внешними. Поскольку внешний элемент имеет отличную от нуля дистанцию до базисного пространства, то каждый внешний элемент — это узел графа, не вошедший в его базис. То есть внешние элементы явно заданы в структуре графа.
Элементы, принадлежащие пространству базиса, никак не проявляются в структуре, — виртуальные элементы (кроме собственно явно заданных вершин базиса). Норма виртуальных элементов равна нулю — это просто нормированный к единице вектор потенциалов на вершинах базиса. Примером виртуального элемента пространства базиса служит ортоцентр базиса.
Если граф представляет собой электрическую цепь, то элементом является совокупность потенциалов на узлах сети. Лапласианом электрической цепи является матрица, состоящая из проводимостей ребер. Умножение данной матрицы на электрические потенциалы узлов дает ток в узлах. Соответственно, потенциалы в узлах являются дистанционными координатами
, а суммарный ток узла — барицентрическими: . Преобразование координат просто отражает закон Ома:В отличие от привычного восприятия пространства, в котором элементы — это нечто материальное, а их компоненты — виртуальны (веса, дистанции, проекции), в пространстве графа ситуация обратная. Компоненты элемента (потенциалы и токи в узлах) материальны, а положение элемента в пространстве как раз виртуально и определяется совокупностью значений компонент.
Построение системы координат на графе
Постановка задачи
Задачу построения системы координат (СК) на графе можно сформулировать следующим образом.
- Задан граф как множество связанных между собой вершин.
- Из множества всех вершин графа выделен базис — набор вершин, для которого можно построить метрический тензор — дистанционный или лапласовский.
- Остальные вершины графа — внешние. Для внешних вершин известны:
- Общая связность вершины (сумма весов ее связей).
- Связи между вершинами.
- Связи внешних вершин с вершинами базиса.
Требуется определить координаты внешних вершин относительно базиса. Система координат должна позволять определять дистанции между всеми (любыми) вершинами графа.
Уточним, что приведена лишь одна из возможных формулировок задачи построения СК. Комбинации известных параметров и тех, что требуется определить, могут варьироваться.
Базисный подграф
Обозначим множество базовых вершин графа индексом
(anchor-якорь), а множество остальных вершин индексом . Объединение данных множеств дает все вершины графа. Считаем узлы графа связанными с остальными хотя бы одной связью.Общий дистанционный метрический тензор (ДМТ) графа
можно разбить на 4 матрицы: — дистанционный метрический тензор подграфа; — матрица ди-координат внешних вершин в базисе . В данной матрице координаты вершины — это столбец матрицы, в транспонированной — строка. — матрица скалярных произведений между вершинами графа, не входящих в базис.По условиям задачи известным является только грамиан подграфа
. Матрицы и — это то, что надо определить на основании данных о структуре графа.Структура лапласиана
Подобным же образом (на 4 подматрицы) можно разбить лапласиан графа
. В отличие от грамиана лапласиан графа здесь минорный — данные об ортоцентре графа отсутствуют. — матрица связей (смежности) между внешними вершинами графа и его базисом . — минор лапласиана, связи внешних вершин. На диагонали данной матрицы находятся значения общей проводимости узла (суммарный вес его ребер), остальные элементы — величина связи узлов между собой. Данная матрица обычно обратима. Ее обращение называется фундаментальной матрицей:Термин «фундаментальная» взят из теории марковских цепей с поглощением. В таких цепях роль базовых играют узлы, из которых нет возврата (поглощающие). Пример использования данной матрицы приводился в статье о способе ранжирования объектов по степени их удаленности от заданных.
Предполагается, что одна из матриц (минор лапласиана
или фундаментальная матрица ) известны. Согласно (4.2) можно выразить одну из другой.Основные тождества
Грамиан и лапласиан графа взаимно обратны.
Для нахождения тождеств, связывающих между собой перечисленные выше матрицы, надо блочные матрицы (4.1.1) и (4.1.2) подставить в (4.3) (лапласиан предварительно окаймить условными параметрами ортоцентра). В итоге получаем следующие соотношения.
Связь лапласовского
и дистанционного метрических тензоров базиса подграфа:(4.4.1) позволяет вычислить один тензор на основании другого. Если базис задан в виде связей, то для определения лапласиана базиса
можно использовать следующее тождество:Здесь
— минор исходного лапласиана на базисных вершинах. — лапласиан, подматрица ЛМТ базиса. На основании данного лапласиана можно найти грамиан подграфа .Если известна матрица связей между внешними узлами графа и его базисом
, а также фундаментальная матрица , то можно рассчитать барицентрические координаты узлов:Матрицу барицентрических координат
называют также матрицей влияния. Действительно, ее значения отражают влияние базовых вершин на остальные (в задаче Дирихле — влияние значений граничных узлов на внешние).Би- и ди-координаты узлов взаимны. Выражаются через метрический тензор базиса:
Ди-координаты включают в себя единицу и значения скалярных произведений элементов с базисом:
.Би-координаты состоят из скалярной компоненты (орбитали) и барицентрических координат:
Если известны детерминанты фундаментальной матрицы и ЛМТ базиса, то можно вычислить общий скалярный потенциал лапласиана графа:
Матрица скалярных произведений внешних вершин
в базисе подграфа представляет собой билинейную форму, выражается через би- или ди-координаты вершин:Фундаментальная матрица и расстояния между вершинами
Очевидно, что значения матрицы
будут в общем случае отличаться от значений скалярных произведений вершин в исходном графе . Разница между ними выражается фундаментальное матрицей:Формула (4.5) может быть использована для вычисления истинного скалярного произведения между вершинами (элементами)
, если известно скалярное произведение элементов в базисе подграфа и фундаментальная матрица .В исходном графе нормы вершин равны нулю. Соответственно, скалярное произведение
может быть выражено через квадрат расстояния между вершинами : . Тогда (4.5) можно представить в виде:С данным выражением мы уже встречались во 2-й части при определении скалярного произведения элементов — (2.6). Сравнивая выражения видим, что значения фундаментальной матрицы можно выразить через скалярное произведение вершин относительно базиса:
Штрихами отмечены проекции вершин на базовое пространство.
— это скалярное произведение пар и .Через
обозначено скалярное произведение нормалей вершин к пространству . 
Нормаль задается как направление из элемента на его проекцию в пространстве базиса. Это близко к определению скалярного произведения координат элементов в обычных системах координат (на векторном базисе), только вместо начала координат здесь указывается пространство.
Если какая-либо из вершин принадлежит базисному пространству, то ее скалярное произведение относительно базиса с любой другой вершиной равно нулю. Таким образом, если один из элементов фундаментальной матрицы равен нулю, то нулевыми будут также вся строка и столбец матрицы.
Если элементы
и совпадают, то значение фундаментальной матрицы равно дистанции от элемента до базового пространства или согласно (2.5) отрицательной норме элемента: — значения диагональных элементов фундаментальной матрицы.Дистанции между элементами вне пространства базиса
Если вершины не принадлежат базовому пространству (принадлежат надпространству), то возможно две ситуации:
1. Вершины принадлежат одному и тому же (над)пространству. В этом случае вершины и их проекции на базовое пространство лежат в одной плоскости.
2. Вершины принадлежат разным (над)пространствам (показано на рисунке выше).
В первой ситуации направление нормалей
и коллинеарно, поэтому скалярное произведение совпадает с произведением расстояний от вершин до базового пространства:Знак квадратного корня положителен, если вершины находятся по одну сторону пространства (нормали направлены в одну сторону) и отрицателен в обратном случае. Данная формула уже приводилась во 2-й статье серии — (2.7). Формула (4.6.3) описывает частный (хотя и важный) случай.
Матрица орбиталей
Для построения системы координат необходимо определить скалярную компоненту би-координат — то, что называется орбиталью элемента. Без данной компоненты дистанции в графе могут быть получены лишь в рамках базового пространства.
Про определении би-координат была получена формула, связывающая орбиталь элемента и его проекции на пространство базиса с нормой элемента — (2.9.1):
Орбиталь проекции элемента можно вычислить через билинейную форму (2.9.2), поскольку нам известна как грамиан базиса
, так и барицентрические координаты элементов (4.4.3). Значения норм элементов согласно (4.6.2) можно взять из диагональных элементов фундаментальной матрицы. Собирая все вместе, получаем выражение для матрицы взаимных орбиталей:Диагональные значения данной матрицы
— это орбитали вершин. Таким образом би-координаты внешних вершин определены. На основании би-координат можно вычислить ди-координаты по формуле (4.4.4), получить матрицу взаимных норм (4.4.2).
Задача построения системы координат выполнена.
Пример построения системы координат
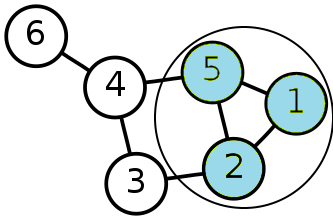
Обратимся к графу, представленному на КДПВ. На нем выделено три базовых вершины — 1, 2 и 5. Требуется определить координаты оставшихся внешних) вершин — 3, 4 и 6.
Вершины базиса могли быть любыми, в том числе не связанными между собой. Хороший базис — это вершины с наибольшей связностью (в нашем графе — это вершины 2, 4, 5). При таком базисе оставшиеся вершины слабо связаны между собой. Минор лапласиана и фундаментальная матрица диагональны (связей нет) и все упрощается. Но нам интересен общий случай, при котором между внешними вершинами есть связи.
Лапласиан:
\begin{array}{c | c c c с c c}
L & 1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1 & 2 & -1 & 0 & 0 & -1 & 0 \\
2 & -1 & 3 & -1 & 0 & -1 & 0 \\
3 & 0 & -1 & 2 & -1 & 0 & 0 \\
4 & 0 & 0 & -1 & 3 & -1 & -1 \\
5 & -1 & -1 & 0 & -1 & 3 & 0 \\
6 & 0 & 0 & 0 & -1 & 0 & 1 \\
\end{array}
Соответствующая матрица дистанций:
\begin{array}{c | c c c с c c}
Q & 1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1 & 0 & 0.(63) & 1.(18) & 1.(18) & 0.(63) & 2.(18) \\
2 & 0.(63) & 0 & 0.(72) & 0.(90) & 0.(54) & 1.(90) \\
3 & 1.(18) & 0.(72) & 0 & 0.(72) & 0.909 & 1.(72) \\
4 & 1.(18) & 0.(90) & 0.(72) & 0 & 0.(72) & 1.00 \\
5 & 0.(63) & 0.(54) & 0.(90) & 0.(72) & 0 & 1.(72) \\
6 & 2.(18) & 1.(90) & 1.(72) & 1.00 & 1.(72) & 0 \\
\end{array}
Грамиан (дистанционный метрический тензор) базиса будет иметь вид (данные взяты из общей дистанционной матрицы графа и поделены на -2):
\begin{array}{c | c c c с}
Gm_{aa} & 0 & 1 & 2 & 5 \\
\hline
0 & 0 & 1 & 1 & 1 \\
1 & 1 & 0 & -0.3(18) & -0.3(18) \\
2 & 1 & -0.3(18) & 0 & -0.(27) \\
5 & 1 & -0.3(18) & -0.(27) & 0 \\
\end{array}
Матрица смежности (связей с базисом) в нашем примере имеет вид:
\begin{array}{c | c c c}
C^{at} & 3 & 4 & 6 \\
\hline
1 & 0 & 0 & 0 \\
2 & 1 & 0 & 0 \\
5 & 0 & 1 & 0 \\
\end{array}
Видим, что 3-я вершина связана со 2-й вершиной базиса, а 4-я с 5-й. 6-я вершина с базисом не связана.
Минор лапласиана внешних связей будет таким:
\begin{array}{c | c c c}
L^{tt} & 3 & 4 & 6 \\
\hline
3 & 2 & -1 & 0 \\
4 & -1 & 3 & -1 \\
6 & 0 & -1 & 1 \\
\end{array}
Исходная триада
— задана. На основании данных матриц можно восстановить все параметры исходного графа.
Обращая минор лапласиана, получаем значения фундаментальной матрицы (4.2):
\begin{array}{c | c c c}
F_{tt} & 3 & 4 & 6 \\
\hline
3 & 2/3 & 1/3 & 1/3 \\
4 & 1/3 & 2/3 & 2/3 \\
6 & 1/3 & 2/3 & 5/3 \\
\end{array}
Барицентрические координаты внешних вершин получаем по формуле (4.4.3):
\begin{array}{c | c c c}
B^{a}_{t} & 3 & 4 & 6 \\
\hline
1 & 0 & 0 & 0 \\
2 & 2/3 & 1/3 & 1/3 \\
5 & 1/3 & 2/3 & 2/3 \\
\end{array}
Видим, что барицентрические координаты вершины 6 совпадают с барицентрическими координатами узла 4. Это характерно для всех узлов, которые соединены только с одной вершиной. Геометрически это означает, что проекции узлов 6 и 4 на пространство базиса совпадают.
Во всех вершинах компонента базовой вершины 1 — нулевая. То есть вклад в барицентрические координаты вершин графа вносят только те вершины, которые с ними связаны — внешние вершины базового подграфа.
Матрица взаимных орбиталей
рассчитывается на основании барицентрических координат и фундаментальной матрицы (4.8):
\begin{array}{c | c c c}
W_{tt} & 3 & 4 & 6 \\
\hline
3 & 0.(54) & 0.(18) & 0.(18) \\
4 & 0.(18) & 0.(54) & 0.(54) \\
6 & 0.(18) & 0.(54) & 1.(54) \\
\end{array}
Теперь можно построить би-координаты элементов
— скалярная компонента равна диагональным значениям матрицы орбиталей, деленным на (-2):
\begin{array}{c | c c c}
Bm^{a}_{t} & 3 & 4 & 6 \\
\hline
0 & -0.(27) & -0.(27) & -0.7(72) \\
1 & 0 & 0 & 0 \\
2 & 0.(6) & 0.(3) & 0.(3) \\
5 & 0.(3) & 0.(6) & 0.(6) \\
\end{array}
Умножая матрицу би-координат на грамиан базиса, получаем ди-координаты.
\begin{array}{c | c c c}
Dm_{at} & 3 & 4 & 6 \\
\hline
0 & 1 & 1 & 1 \\
1 & -0.5(90) & -0.5(90) & -1.(09) \\
2 & -0.(36) & -0.(45) & -0.9(54) \\
5 & -0.(45) & -0.(36) & -0.8(63) \\
\end{array}
Дистанция между вершинами графа 6 и 1 согласно данной матрице должна быть равна
. Посмотрев на общую дистанционную матрицу, можно убедиться, что так и есть.
Матрица скалярных произведений в подграфе — это произведение взаимных координат вершин:
\begin{array}{c | c c c}
N_{tt} & 3 & 4 & 6 \\
\hline
3 & -0.(6) & -0.(69) & -1.1(96) \\
4 & -0.(69) & -0.(6) & -1.1(6) \\
6 & -1.1(96) & -1.1(6) & -1.(6) \\
\end{array}
Согласно данной матрице все внешние вершины графа лежат вне базового пространства (нормы ненулевые). Осталось определить дистанции между внешними вершинами. Используем (4.5'):
\begin{array}{c | c c c}
Q_{tt} & 3 & 4 & 6 \\
\hline
3 & 0 & 0.(72) & 1.(72) \\
4 & 0.(72) & 0 & 1.0 \\
6 & 1.(72) & 1.0 & 0 \\
\end{array}
Сравниваем с исходной дистанционной матрицей
и убеждаемся, что все значения совпадают.
Граф из 6 вершин с базисом из 3-х
Обратимся к графу, представленному на КДПВ. На нем выделено три базовых вершины — 1, 2 и 5. Требуется определить координаты оставшихся внешних) вершин — 3, 4 и 6.
Вершины базиса могли быть любыми, в том числе не связанными между собой. Хороший базис — это вершины с наибольшей связностью (в нашем графе — это вершины 2, 4, 5). При таком базисе оставшиеся вершины слабо связаны между собой. Минор лапласиана и фундаментальная матрица диагональны (связей нет) и все упрощается. Но нам интересен общий случай, при котором между внешними вершинами есть связи.
Исходный граф — для проверки
Лапласиан:
\begin{array}{c | c c c с c c}
L & 1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1 & 2 & -1 & 0 & 0 & -1 & 0 \\
2 & -1 & 3 & -1 & 0 & -1 & 0 \\
3 & 0 & -1 & 2 & -1 & 0 & 0 \\
4 & 0 & 0 & -1 & 3 & -1 & -1 \\
5 & -1 & -1 & 0 & -1 & 3 & 0 \\
6 & 0 & 0 & 0 & -1 & 0 & 1 \\
\end{array}
Соответствующая матрица дистанций:
\begin{array}{c | c c c с c c}
Q & 1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1 & 0 & 0.(63) & 1.(18) & 1.(18) & 0.(63) & 2.(18) \\
2 & 0.(63) & 0 & 0.(72) & 0.(90) & 0.(54) & 1.(90) \\
3 & 1.(18) & 0.(72) & 0 & 0.(72) & 0.909 & 1.(72) \\
4 & 1.(18) & 0.(90) & 0.(72) & 0 & 0.(72) & 1.00 \\
5 & 0.(63) & 0.(54) & 0.(90) & 0.(72) & 0 & 1.(72) \\
6 & 2.(18) & 1.(90) & 1.(72) & 1.00 & 1.(72) & 0 \\
\end{array}
Входные данные
Грамиан (дистанционный метрический тензор) базиса
будет иметь вид (данные взяты из общей дистанционной матрицы графа и поделены на -2):\begin{array}{c | c c c с}
Gm_{aa} & 0 & 1 & 2 & 5 \\
\hline
0 & 0 & 1 & 1 & 1 \\
1 & 1 & 0 & -0.3(18) & -0.3(18) \\
2 & 1 & -0.3(18) & 0 & -0.(27) \\
5 & 1 & -0.3(18) & -0.(27) & 0 \\
\end{array}
Матрица смежности (связей с базисом)
в нашем примере имеет вид:\begin{array}{c | c c c}
C^{at} & 3 & 4 & 6 \\
\hline
1 & 0 & 0 & 0 \\
2 & 1 & 0 & 0 \\
5 & 0 & 1 & 0 \\
\end{array}
Видим, что 3-я вершина связана со 2-й вершиной базиса, а 4-я с 5-й. 6-я вершина с базисом не связана.
Минор лапласиана внешних связей
будет таким:\begin{array}{c | c c c}
L^{tt} & 3 & 4 & 6 \\
\hline
3 & 2 & -1 & 0 \\
4 & -1 & 3 & -1 \\
6 & 0 & -1 & 1 \\
\end{array}
Исходная триада
— задана. На основании данных матриц можно восстановить все параметры исходного графа.Восстанавливаем граф
Обращая минор лапласиана
, получаем значения фундаментальной матрицы (4.2):\begin{array}{c | c c c}
F_{tt} & 3 & 4 & 6 \\
\hline
3 & 2/3 & 1/3 & 1/3 \\
4 & 1/3 & 2/3 & 2/3 \\
6 & 1/3 & 2/3 & 5/3 \\
\end{array}
Барицентрические координаты внешних вершин
получаем по формуле (4.4.3):\begin{array}{c | c c c}
B^{a}_{t} & 3 & 4 & 6 \\
\hline
1 & 0 & 0 & 0 \\
2 & 2/3 & 1/3 & 1/3 \\
5 & 1/3 & 2/3 & 2/3 \\
\end{array}
Видим, что барицентрические координаты вершины 6 совпадают с барицентрическими координатами узла 4. Это характерно для всех узлов, которые соединены только с одной вершиной. Геометрически это означает, что проекции узлов 6 и 4 на пространство базиса совпадают.
Во всех вершинах компонента базовой вершины 1 — нулевая. То есть вклад в барицентрические координаты вершин графа вносят только те вершины, которые с ними связаны — внешние вершины базового подграфа.
Матрица взаимных орбиталей
рассчитывается на основании барицентрических координат и фундаментальной матрицы (4.8):\begin{array}{c | c c c}
W_{tt} & 3 & 4 & 6 \\
\hline
3 & 0.(54) & 0.(18) & 0.(18) \\
4 & 0.(18) & 0.(54) & 0.(54) \\
6 & 0.(18) & 0.(54) & 1.(54) \\
\end{array}
Теперь можно построить би-координаты элементов
— скалярная компонента равна диагональным значениям матрицы орбиталей, деленным на (-2):\begin{array}{c | c c c}
Bm^{a}_{t} & 3 & 4 & 6 \\
\hline
0 & -0.(27) & -0.(27) & -0.7(72) \\
1 & 0 & 0 & 0 \\
2 & 0.(6) & 0.(3) & 0.(3) \\
5 & 0.(3) & 0.(6) & 0.(6) \\
\end{array}
Умножая матрицу би-координат на грамиан базиса, получаем ди-координаты
.\begin{array}{c | c c c}
Dm_{at} & 3 & 4 & 6 \\
\hline
0 & 1 & 1 & 1 \\
1 & -0.5(90) & -0.5(90) & -1.(09) \\
2 & -0.(36) & -0.(45) & -0.9(54) \\
5 & -0.(45) & -0.(36) & -0.8(63) \\
\end{array}
Дистанция между вершинами графа 6 и 1 согласно данной матрице должна быть равна
. Посмотрев на общую дистанционную матрицу, можно убедиться, что так и есть.Матрица скалярных произведений в подграфе
— это произведение взаимных координат вершин:\begin{array}{c | c c c}
N_{tt} & 3 & 4 & 6 \\
\hline
3 & -0.(6) & -0.(69) & -1.1(96) \\
4 & -0.(69) & -0.(6) & -1.1(6) \\
6 & -1.1(96) & -1.1(6) & -1.(6) \\
\end{array}
Согласно данной матрице все внешние вершины графа лежат вне базового пространства (нормы ненулевые). Осталось определить дистанции между внешними вершинами
. Используем (4.5'):\begin{array}{c | c c c}
Q_{tt} & 3 & 4 & 6 \\
\hline
3 & 0 & 0.(72) & 1.(72) \\
4 & 0.(72) & 0 & 1.0 \\
6 & 1.(72) & 1.0 & 0 \\
\end{array}
Сравниваем с исходной дистанционной матрицей
и убеждаемся, что все значения совпадают.Маловершинные базисы
Если базис содержит небольшое количество вершин, то часть формул обращения (4.4) может быть выражена в явном виде. Здесь рассмотрим базисы из одной и двух вершин.
Базис из одной вершины
Достаточно тривиален и поэтому не очень интересен. Дистанционный метрический тензор базиса не включает ни одной дистанции:
Все барицентрические координаты вершин относительно базиса равны 1 (поскольку всего одна компонента). Фундаментальная матрица совпадает с матрицей скалярных произведений пар, где первым элементом каждой пары является как раз вершина базиса. В 3-й части было показано, что дистанционную матрицу на основании такой матрицы можно получить через преобразование дистанции:
Базис из двух вершин
Такой базис имеет прикладное значение. Например, в рассмотренной нами ранее задаче электрометрии узлы, к которым прикладывается внешнее напряжение, — это и есть 2-вершинный базис.
Обозначим дистанцию между базовыми вершинами
и как . Напомним, что в электрической цепи дистанция эквивалентна сопротивлению между узлами. Тогда дистанционный метрический тензор базиса имеет вид:Детерминант ДМТ:
. Лапласовский тензор (ЛМТ) получаем обращением дистанционного (4.4.1):Ди-координаты вершин графа будут иметь три компоненты: скалярная (1), скалярные произведения
относительно базовой вершины и скалярные произведения относительно базовой вершины :Би-координаты также имеют три компоненты. Скалярная компонента — это (геометрическая) орбиталь вершины.
Подставляя (4.11.1) в (4.4.5) и учитывая (3.8), получаем выражения для компонент би-координат вершины P:
Здесь через
обозначено скалярное произведение пар, начало которых находится в вершине , а концы — в элементах и .Можно убедиться, что сумма барицентрических компонент равна 1, как и должно быть:
.Разность потенциалов графа при 2-вершинном базисе
Барицентрическая часть координат в (4.12) представляет собой матрицу влияния — передает влияние базовых вершин на внешние. Если, например, на базовых вершинах заданы значения потенциалов
, то потенциалы остальных вершин определяются произведением заданных потенциалов на матрицу влияния:Пусть вектор заданных потенциалов имеет вид
. Тогда разность потенциалов между элементами P и Q графа будет равна:При выводе использовано тождество (3.9.4) для разности скалярных произведений смежных пар.
— это величина входящего потока, определяется уравнением .Формула (4.15) в явном виде выражает связь разностей потенциалов на вершинах графа со скалярным произведением, на что было указано в предыдущей статье.
Подведем итоги. В данной части показано, как задать на графе систему координат. Приведены основные тождества, ключевыми из которых на наш взгляд являются (4.5) и (4.5.1).
Из обязательной программы осталось рассмотреть преобразование координат (смену базиса), чем и займемся в следующей статье.
