
На рисунке — первый в мире спутник квантовой связи «Мо-Цзы», который запустили из Китая в 2016 году, в нем летает TDC, реализованная в FPGA.
Объяснить своей девушке (или парню), что такое ADC и DAC, и в каких домашних приборах они используются, может каждый человек, называющий себя инженером. А вот что такое TDC, и почему у нас дома их нет, зачастую можно узнать только после свадьбы.
TDC — это time-to-digital converter. По-русски говоря: времяизмерительная система.
Основные потребители быстродействующих TDC — научные группы. Как правило, под определенный исследовательский проект требуется что-то очень специфическое. То каналов надо много, то разрешение очень высокое, то исполнение компактное. А уровень развития современных FPGA и их доступность как раз дают исследователям возможность экспериментировать с реализациями и подстраивать их под собственные нужды.
В этой хабрастатье приводится детальное описание простенькой времяизмерительной системы на FPGA Cyclone IV. Статья будет полезна не только для расширения кругозора, но и с методической точки зрения, поскольку реализация системы нетривиальная.
Сразу отметим, что пришедшая на ум мысль «Да о чем они тут пишут? Считываем по событию счетчик/таймер CPU/MCU и дело в шляпе» тут не годится. Дело в том, что в приложениях требуется точность на порядок большая, чем могут обеспечить «стандартные» счетчики, а также детерминированная латентность, многоканальность и большая «пропускная способность событий».
Формально задача, которую решает TDC, — определение временного интервала между событиями. В многоканальных системах логика верхнего уровня дополнительно может вычислять корреляции между событиями. В качестве события, как правило, выступает срабатывание какого-либо детектора частиц или оптического датчика. В быту, конечно, такие системы не находят применения. И вообще, в масштабе пикосекунд имеет смысл измерять физические процессы, протекающие в сравнимых временах, например, пролет элементарных частиц в детекторе. Отметим некоторые направления применения TDC:
- Масспектроскопия, позитронно-эмиссионная томография (ПЭТ) — регистрируются времена прихода частиц на детекторы.
- ЛИДАРы — по временным отсчетам определяется расстояние до облученной области.
- Квантовая криптография — регистрируются времена срабатывания детекторов одиночных фотонов.
- Генерация случайных чисел — времена наступления событий используются в качестве энтропии.
Электрический импульс, сгенерированный детектором, проходит схему предобработки, которая переводит его в «удобоваримый» для электроники вид. То есть иголка (glitch) превращается в сигнал длительностью несколько наносекунд с амплитудой несколько вольт. В зависимости от реализации эта схема может располагаться непосредственно в детекторе или во времяизмерительной системе. Ниже приведена временная диаграмма выходного сигнала детектора одиночных фотонов ID Quantique. На картинке помимо самого импульса видно так называемое «мертвое время» детектора. Это интервал времени в течение которого детектор не реагирует на внешние события. Поскольку это время возникает из особенностей электронных схем, то и сами TDC обладают некоторым мертвым временем, с которым разработчики непрерывно борются.

Для высокоточного измерения временных интервалов на рынке доступны как коробочные решения, так и специализированные ASIC. По теме реализации TDC имеется достаточно обширный материал. С общей теорией можно ознакомиться в книге Time-to-Digital Converters Стефана Ханцлера, а с различными современными реализациями в периодических публикациях, например, на arxiv.org. Мы же поговорим о простой FPGA-шной реализации TDC.
Реализация TDC в FPGA
С электронной точки зрения реализация задача сводится к «регистрированию положения» фронта сигнала относительно какого-либо синхросигнала. Элементы FPGA, имеющиеся в нашем распоряжении, это физически линии сигналов на кристалле, регистры, логические блоки, линии клока и PLL. Основные подходы к реализации TDC с использованием этих элементов были предложены относительно давно: субтактовая линия задержки (tapped delay line), линия задержки Вернье (Vernier delay line), «фазированные PLL». Но инженеры до сих пор работают над их усовершенствованием и имплементацией на современных платформах.
В нашей FPGA-шной реализации мы в основном следовали этой публикации, описывающей субтактовую линию задержки, а также некоторым общим идеям, почерпнутым в публикациях Jinyuan Wu из CERN`а 2000-x годов.
Концепция субтактовой линии задержки приведена на рисунках ниже (анимация взята из презентации Jinyuan Wu, Z. Shi и I. Wang). Суть: пропустить входной сигнал через цепь, сформированную элементами задержки, выходы которых подключены к одновременно защелкивающимся регистрам. В результате значения, защелкнутые в наборе регистров — термокод, соответствуют взаимному расположению фронтов входного и синхросигналов. Дальше уже все просто. Корректируем ошибки в термокоде, декодируем в число, сбрасываем значения регистров, дописываем номер такта, в котором зарегистрировано событие, и передаем на выход.


Вспоминаем устройство FPGA семейства Cyclone от компании Intel (Altera). Логические элементы (LE) сгруппированы в блоки (LAB), управляемые одной линией клока и соединены линиями переноса разряда (carry line). Это как раз нужная нам схема. То есть входной сигнал будем заводить на какой-нибудь LE и направлять его по линиям переноса разряда на соседние. При этом LE должны работать в арифметическом режиме. Тактировать все LE будем одним клоком и забирать термокод по появлению входного сигнала.
Теперь перед нами стоят несколько практических вопросов:
- Как описать схему линии задержки на Verilog?
- Как объяснить Quartus`у, что мы хотим использовать именно линии переноса и отключить их оптимизацию?
- Как сформировать линию задержки на соседних LE из одного LAB?
Язык описания схем Verilog не позволяет описать синтезируемые задержки. Задержки, задаваемые инструкцией #N, предназначены для симуляции. Но в нашем случае этого и не требуется. Ключ в том, чтобы описать использование LE определенным способом.
Для этого в библиотеки элементов от Intel идет IP-блок описания LE. Этот модуль общий для LE-семейства Cyclone, и в нашем случае некоторые его параметры не задействованы.
С точки зрения Quartus`а, линия задержки — штука бессмысленная. Зачем вести сигнал хитрым способом, если его сразу можно провести из точки A в точку B? Для того чтобы Quartus не пытался оптимизировать линию задержки, и результате выкинул составляющие ее LE, используем директиву /* synthesis keep = 1 */ напротив объявления элемента, к которому она относится. В результате основной код выглядит следующим образом:
// Первый элемент линии задержки
cyclone_lcell
#(
.operation_mode ("arithmetic" ), // «арифметический» режим работы
.synch_mode ("off" ),
.register_cascade_mode ("off" ),
.sum_lutc_input ("datac" ),
.lut_mask ("cccc" ), // «формула» арифметического блока
.power_up ("low" ),
.cin_used ("false" ),
.cin0_used ("false" ),
.cin1_used ("false" ),
.output_mode ("reg_and_comb" ), // используем логику и выходной регистр
.lpm_type ("cyclone_lcell"),
.x_on_violation ("off" )
)
u_cell0( /* synthesis keep = 1 */
.clk ( clk ), // входной клок
.dataa ( 0 ),
.datab ( in_hit ), // входной сигнал
.datac ( 0 ),
.aclr ( 0 ),
.aload ( 0 ),
.sclr ( 0 ),
.sload ( 0 ),
.ena ( 1 ),
.inverta ( 0 ),
.regcascin ( 0 ),
.combout ( ),
.regout ( r_out[0] ), // выходной регистр
.cout ( c_out[0] ) // линия переноса разряда
);
// Последующие элементы линии задержки
genvar i;
generate for (i = 1; i < DELAY_STAGES; i = i + 1)
begin : DELAY_LINE
cyclone_lcell
#(
.operation_mode ("arithmetic" ), // «арифметический» режим работы
.synch_mode ("off" ),
.register_cascade_mode ("off" ),
.sum_lutc_input ("cin" ),
.lut_mask ("f0f0" ), // «формула» арифметического блока
.power_up ("low" ),
.cin_used ("true" ), // используем линию переноса
.cin0_used ("false" ),
.cin1_used ("false" ),
.output_mode ("reg_and_comb" ), // используем логику и выходной регистр
.lpm_type ("cyclone_lcell"),
.x_on_violation ("off" )
)
u_cell1( /* synthesis keep = 1 */
.clk ( clk ), // входной клок
.dataa ( 0 ),
.datab ( 0 ),
.datac ( 0 ),
.cin ( c_out[i-1] ), // входной сигнал
.aclr ( 0 ),
.aload ( 0 ),
.sclr ( 0 ),
.sload ( 0 ),
.ena ( 1 ),
.inverta ( 0 ),
.regcascin ( 0 ),
.combout ( ),
.regout ( r_out[i] ), // выходной регистр
.cout ( c_out[i] ) // линия переноса разряда
);
end
endgenerate Для указания на использование соседних LE и их размещения в конкретном месте на кристалле применим инструмент LogicLock Regions. То есть укажем на кристалле прямоугольную область и явно укажем набор LE, которые Quartus должен в ней разместить. На рисунке ниже область line содержит линию задержки, а область delay_line включает дополнительную логику обработки термокода.

Ниже приведем схему размещения элементов линии задержки из Chip Planner со схематическим отображением сигналов и детальную схему первых двух элементов линии задержки.
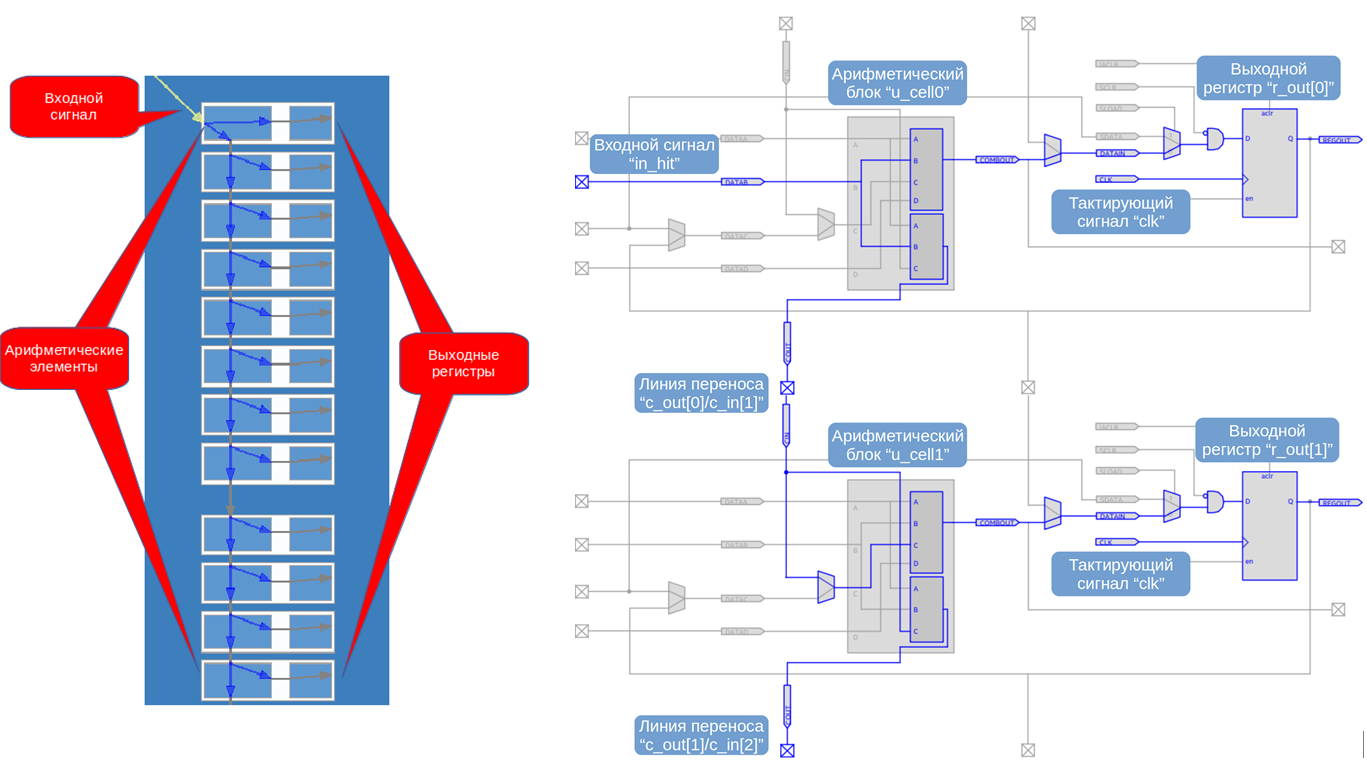
Отметим, что реализованная схема имеет мертвое время в один такт, необходимое для «сброса» регистров линии задержки.
Описанная схема была разложена на чипе Cyclone IV EP4CE22. Эксперименты с длиной линии задержки и частотой клока привели к следующим параметрам: длина линии задержки 64 LE, частота клока ~120МГц. Линия задержки и логика обработки термокода умещаются в 42 LABs.
Калибровка TDC
Очевидно, что физические задержки на каждом логическом элементе отличаются. Для учета этого факта необходимо провести калибровку устройства. Первым, что приходит в голову, видится подача на вход TDC сигнала с известным периодом. Однако такой путь является достаточно трудоемким, поскольку требуется прецизионное сканирование периода сигнала в относительно широком диапазоне.
Следующим предложением является калибровка методом случайных событий: подаем на вход сигналы с равномерно распределенными случайными задержками и наблюдаем гистограмму попадания событий в тайм-бины. В этом случае точность растет по мере накопления событий как
Суть способа в подборе частоты генерации событий, при которой они будут равномерно распределены в тайм-бинах. Для этого необходимо удовлетворить соотношению:
где N — число событий, которые мы хотим равномерно распределить в временном интервале T1, 1/T2 — частота генерации событий, {…} — дробная часть числа.
При этом сигналы могут быть сформированы внутренним PLL. В нашем примере входная частота PLL равна 50МГц и для числа событий N = 256 мы выбрали следующие рабочие частоты:
- 1/T1 = 50МГц * 93/40 = 116.26МГц: частота клока TDC
- 1/T2 = 50МГц * 32/285 = 5.614МГц: частота генерации событий
Соотношение таково, что на приблизительно двадцать тактов TDC приходится одно событие. При этом разрешение между соседними событиями равно:
Процедура калибровки заключается в многократном измерении непрерывной последовательности из 256 событий. В нашем эксперименте общее число измеренных событий равно 8192. Полученная в результате гистограмма соответствует доле отдельных элементов задержки в одном такте TDC.
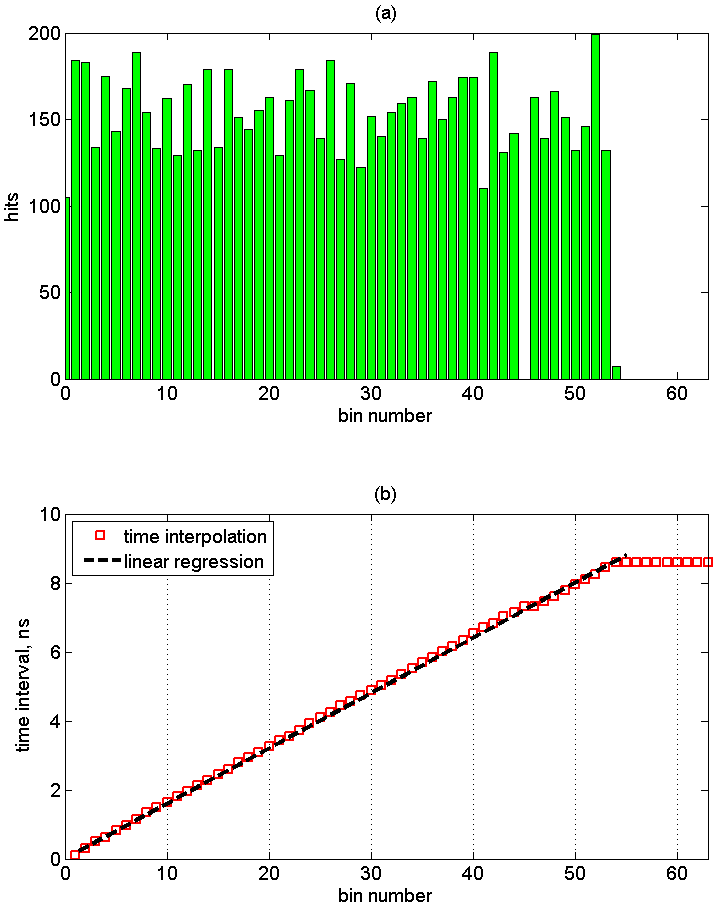
На верхнем графике приведено распределение отсчетов по элементам линии задержки. Номер отсчета следует понимать как границу между единицами и нулями в скорректированном термокоде. Провал на 45-м элементе линии задержки соотвует одновременному срабатыванию двух соседних элементов, что является характерным для подобной реализации (bubble error [Wu08]). Положение провала зависит от области размещения линии задержки на кристалле. При увеличении числа регистрируемых событий не происходит существенного изменения распределения отсчетов.
На нижнем графике приведена калибровочная кривая, сопоставляющая номер интервала с длительностью задержки. Сумма всех отсчетов по тайм-бинам соответствует времени T1 = 8.6нс. Перевод номера бина во временные интервалы может осуществляться непосредственно в кристалле или с помощью программируемого процессора Nios II.
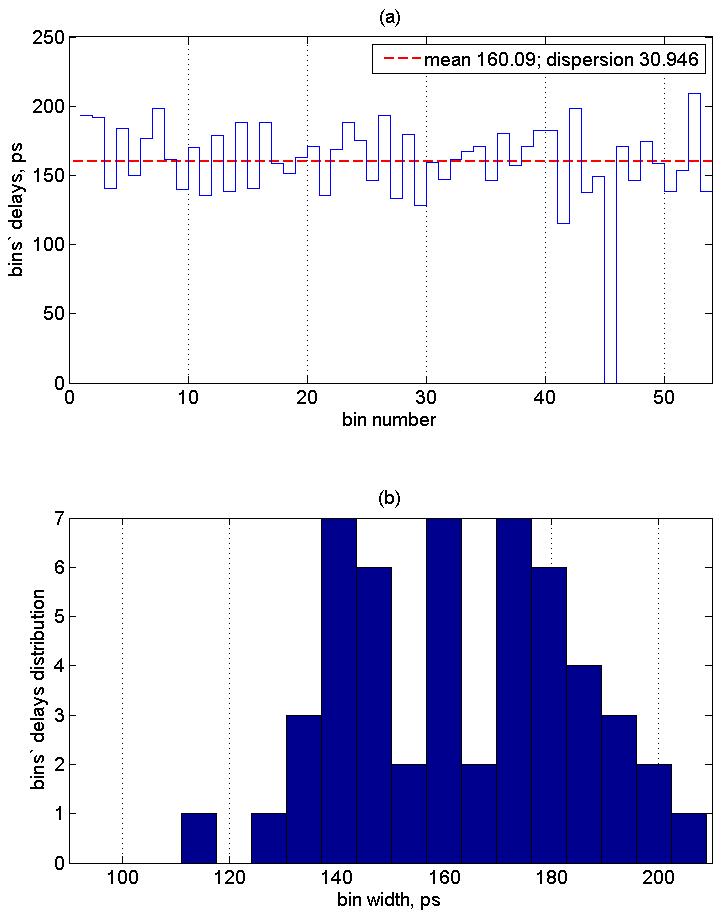
Далее приведены абсолютные временные интервалы соотвующие элементам линии задержки с существенным числом срабатываний и распределение интервалов. Среднее значение интервала равно 160 ps, дисперсия времен — 31 ps. В результате, можно утверждать, что достигнутое разрешение времяизмерительной системы составляет ~200 ps. Чтобы почувствовать это число отметим, что оно соответствует частоте 5ГГц. И это только самая простая реализация в FPGA не на самом последнем кристалле!
Заключение
Мы рассмотрели некоторые моменты реализации TDC в FPGA. Однако значительная часть деталей опущена. Если вам интересна эта тема, советуем познакомиться с такими штуками, как динамическая калибровка; методы коррекции ошибок (bubble errors), повышения разрешения TDC (wavelauncher), уменьшения неопределенности интервала (averaging, multiple TDC instances), уменьшения мертвого времени. Также можно рассмотреть реализацию TDC на альтернативных платформах.