Часть 1. Математика

Введение
Мы так привыкли к взаимодействию с окружающим нас миром, что не задумываемся о том, насколько сложно двигаются наши руки и ноги. В академической литературе задача управления манипулятором робота называется инверсной кинематикой. Кинематика обозначает "движения", а понятие "инверсная" связано с тем, что обычно мы не управляем самой рукой. Мы управляем «двигателями», поворачивающими каждую отдельную часть. Инверсная кинематика — это задача определения того, как перемещать эти двигатели, чтобы сдвинуть руку в конкретную точку. И в своём общем виде эта задача чрезвычайно сложна. Чтобы вы понимали, насколько она сложна, то можете вспомнить о таких играх, как QWOP, GIRP или даже Lunar Lander, в которой вы выбираете не куда двигаться, а какие мускулы (или ускорители) приводить в действие.
Задача управления подвижными приводами распостраняется даже на область робототехники. Вас не должно удивлять то, что на протяжении веков математики и инженеры смогли разработать множество решений. В большинстве 3D-редакторов и игровых движков (в том числе и в Unity) есть наборы инструментов, позволяющих выполнять риггинг человекоподобных и звероподобных существ. Для различных схем (манипуляторов роботов, хвостов, щупалец, крыльев и т.д.) встроенных решений обычно не существует.
Именно поэтому в предыдущей серии статей по процедурным анимациям и инверсной кинематике я предложил очень общее и эффективное решение, способное работать при любой схеме. Но такая мощь имеет свой компромисс: эффективность. Одной из важнейших причин критики моей статьи было то, что способ оказался слишком долгим и затратным при одновременном использовании для сотен персонажей. Поэтому я решил написать новую статью, посвящённую инверсной кинематике манипулятора в двух степенях свободы. Описанная в этом туториале техника чрезвычайно эффективна и может использоваться для десятков (если не сотен!) персонажей одновременно.
Инверсная кинематика
Давайте представим манипулятор робота с двумя сегментами и двумя шарнирами, похожий на показанную ниже схему. На конце манипулятора есть конечное звено, которым мы хотим управлять. Мы не имеем непосредственного контроля над позицией конечного звена и можем только поворачивать шарниры. Задача инверсной кинематики заключается в нахождении наилучшего способа поворота соединений для перемещения конечного звена в нужную позицию.

Решение, предлагаемое в этом туториале, будет работать только для манипуляторов с двумя шарнирами. В академической литературе часто пишут, что такие манипуляторы обладают двумя степенями свободы. И причина этого совершенно понятна из показанной ниже схемы. Манипулятор робота с двумя степенями свободы можно смоделировать в виде треугольника, который является одной из самых хорошо изученных фигур в геометрии.

Давайте начнём с того, что немного формализируем задачу. Два шарнира,
Внутренние углы
Мы можем использовать три точки

Хотя все три угла нам неизвестны, мы знаем длину всех рёбер.
- Отрезок
обозначает руку и имеет длину
;
- Отрезок
обозначает предплечье и имеет длину
;
- Отрезок
обозначает расстояние между шарниром плеча и кистью, и имеет длину
.
Знания трёх сторон треугольника достаточно для нахождения всех трёх углов. Это возможно благодаря теореме косинусов, которая является обобщением теоремы Пифагора для треугольников, которые необязательно являются правильными.
Двумя углами, необходимыми для управления манипулятором, являются и
. Давайте начнём с
, который можно вычислить с помощью теоремы косинусов:
Мы можем преобразовать уравнение, чтобы перенести
Теперь нам нужно применить обратную косинусу функцию
С помощью такой же процедуры мы можем снова применить теорему косинусов, чтобы найти
Вывод теоремы косинусов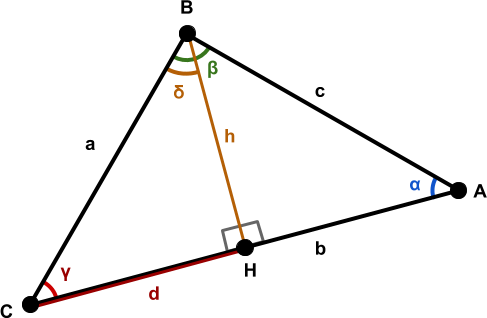
Отрезок делит треугольник
делит треугольник  на два правильных треугольника:
на два правильных треугольника:  и
и  . Это доказательство является естественным следствием из применения к обоим треугольникам теоремы Пифагора:
. Это доказательство является естественным следствием из применения к обоим треугольникам теоремы Пифагора:
Оба уравнения теперь представлены относительно . Мы можем приравнять их оба, чтобы получить следующее:
. Мы можем приравнять их оба, чтобы получить следующее:
что можно преобразовать в:
В таком виде теорема косинусов представлена в «Началах» Евклида.
Чтобы получить современный вид уравнения, нам нужно применить тригонометрию. Так как (5) является правильным треугольником, мы можем выразить отрезок как:
как:
где можно найти, вспомнив, что сумма углов треугольника равна
можно найти, вспомнив, что сумма углов треугольника равна  (или, что аналогично,
(или, что аналогично,  радианам):
радианам):
Подставив , мы получаем:
, мы получаем:
Последним шагом будет хорошо известное свойство:
Теперь мы можем подставляем это, что даёт нам современный вид теоремы косинусов:

Отрезок
Оба уравнения теперь представлены относительно
что можно преобразовать в:
В таком виде теорема косинусов представлена в «Началах» Евклида.
Чтобы получить современный вид уравнения, нам нужно применить тригонометрию. Так как (5) является правильным треугольником, мы можем выразить отрезок
где
Подставив
Последним шагом будет хорошо известное свойство:
Теперь мы можем подставляем это, что даёт нам современный вид теоремы косинусов:
Углы шарниров
С помощью теоремы косинусов мы вычислили значения

Давайте начнём с вычисления
Вычисление
Что даёт нам:
Знак углов
Множественные решения?
Задача инверсной кинематики обычно предполагает несколько решений. Даже в нашем случае со всего двумя степенями свободы у нас есть два разных решения.
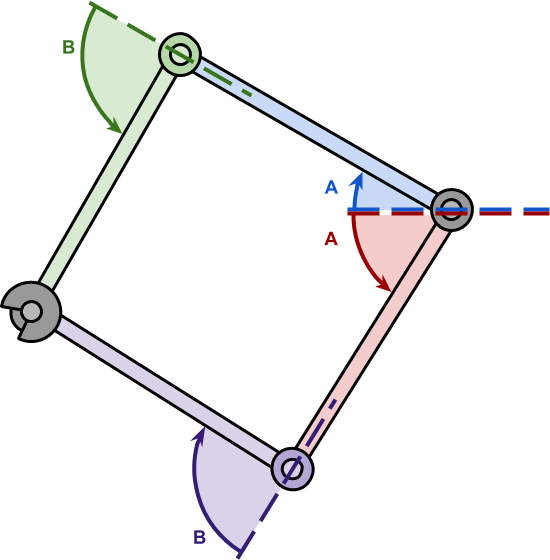
Хотя углы и
и  на самом деле различны, вывод по сути остаётся тем же, за небольшими исключениями.
на самом деле различны, вывод по сути остаётся тем же, за небольшими исключениями.

Хотя углы
Часть 2. Код

Введение
В предыдущей части мы рассмотрели задачу инверсной кинематики для манипулятора робота с двумя степенями свободы.
В таком случае обычно известна длина манипуляторов

Затем мы вывели уравнения для углов
С первого взгляда они могут выглядеть довольно пугающими; с другой стороны, их геометрическая интерпретация достаточно интуитивно понятна из показанного выше рисунка.
Создание манипулятора робота
Первым шагом по реализации этого решения является создание манипулятора робота. Концепция «шарниров» неизвестна движку Unity. Однако имеющуюся в движке систему родительских элементов можно использовать для создания иерархии компонентов, которые будут вести себя в точности как манипулятор робота.
Идея заключается в использовании для каждого шарнира
GameObject, чтобы поворот его transform заставлял поворачиваться и прикреплённый к нему манипулятор. Сделав второй шарнир дочерним элементом первого шарнира, мы заставим их поворачиваться как на первом рисунке.В результате мы получим такую иерархию:
- Корень
- Шарнир A
- Кость A
- Шарнир B
- Кость B
- Рука
- Шарнир A
Затем мы можем добавить корневому объекту скрипт с названием
SimpleIK, который будет выполнять повороты шарниров для достижения нужной точки.using System.Collections;
using UnityEngine;
namespace AlanZucconi.IK
{
public class SimpleIK : MonoBehaviour
{
[Header("Joints")]
public Transform Joint0;
public Transform Joint1;
public Transform Hand;
[Header("Target")]
public Transform Target;
...
}
}Выведенные в предыдущей части туториала уравнения требуют знания длины первых двух костей (называемых соответственно
Start. Однако это требует, чтобы манипулятор находился при запуске игры в хорошей конфигурации.private length0;
private length1;
void Start ()
{
length0 = Vector2.Distance(Joint0.position, Joint1.position);
length1 = Vector2.Distance(Joint1.position, Hand.position );
}Повороты шарниров
Прежде чем показывать готовую версию кода, давайте начнём с упрощённой. Если мы перенесём уравнения (1) и (2) непосредственно в код, то в результате получим что-то подобное:
void Update ()
{
// Расстояние от Joint0 до Target
float length2 = Vector2.Distance(Joint0.position, Target.position);
// Внутренний угол альфа
float cosAngle0 = ((length2 * length2) + (length0 * length0) - (length1 * length1)) / (2 * length2 * length0);
float angle0 = Mathf.Acos(cosAngle0) * Mathf.Rad2Deg;
// Внутренний угол бета
float cosAngle1 = ((length1 * length1) + (length0 * length0) - (length2 * length2)) / (2 * length1 * length0);
float angle1 = Mathf.Acos(cosAngle1) * Mathf.Rad2Deg;
// Угол между Joint0 и Target
Vector2 diff = Target.position - Joint0.position;
float atan = Mathf.Atan2(diff.y, diff.x) * Mathf.Rad2Deg;
// Вот как они получаются в системе отсчёта Unity
float jointAngle0 = atan - angle0; // Угол A
float jointAngle1 = 180f - angle1; // Угол B
...
}Математические функции
Mathf.Acos и Mathf.Atan2. Кроме того, окончательные углы преобразуются в градусы с помощью Mathf.Rad2Deg, потому что компонент Transform должен получать углы, а не радианы.Нацеливаемся на недостижимые цели
Хотя показанный выше код кажется рабочим, существует условие, при котором он терпит неудачу. Что произойдёт, если цель недостижима? В текущей реализации это не учитывается, что приводит к нежелательным поведениям.
Обычным решением будет полное растяжение манипулятора в направлении цели. Такое поведение соответствует движению дотягивания, которое мы стремимся симулировать.
Показанный ниже код распознаёт недостижимые цели, проверяя больше ли расстояние от корня до неё общей длины манипулятора.
void Update ()
{
float jointAngle0;
float jointAngle1;
float length2 = Vector2.Distance(Joint0.position, Target.position);
// Угол между Joint0 и Target
Vector2 diff = Target.position - Joint0.position;
float atan = Mathf.Atan2(diff.y, diff.x) * Mathf.Rad2Deg;
// Достижима ли цель?
// Если нет, то мы растягиваемся как можно дальше
if (length0 + length1 < length2)
{
jointAngle0 = atan;
jointAngle1 = 0f;
}
else
{
float cosAngle0 = ((length2 * length2) + (length0 * length0) - (length1 * length1)) / (2 * length2 * length0);
float angle0 = Mathf.Acos(cosAngle0) * Mathf.Rad2Deg;
float cosAngle1 = ((length1 * length1) + (length0 * length0) - (length2 * length2)) / (2 * length1 * length0);
float angle1 = Mathf.Acos(cosAngle1) * Mathf.Rad2Deg;
// Вот как определяются углы в системе отсчёта Unity
jointAngle0 = atan - angle0;
jointAngle1 = 180f - angle1;
}
...
}Повороты шарниров
Теперь нам осталось научиться поворачивать шарниры. Это выполняется при помощи доступа к свойству
localEulerAngles компонента Transform шарниров. К сожалению, мы не можем изменять угол z напрямую, поэтому вектор необходимо копировать, изменять и вставлять значение.Vector3 Euler0 = Joint0.transform.localEulerAngles;
Euler0.z = jointAngle0;
Joint0.transform.localEulerAngles = Euler0;
Vector3 Euler1 = Joint1.transform.localEulerAngles;
Euler1.z = jointAngle1;
Joint1.transform.localEulerAngles = Euler1;На этом туториал по инверсной кинематике для двухмерных манипуляторов завершается.