For me, these two models are quite similar, but in fact they don’t have obvious characteristics to measure this similarity. These models have different numbers of vertices, edges and polygons. They are of different sizes, rotated differently and both have the same transforms (Location = [0,0,0], Rotation in radians = [0,0,0], Scale = [1,1,1]). So how to determine their similarity?
If these models were equally oriented in space, they could be scaled to the common size of Bounding Box, then move the origin of local coordinates to its center, convert models to voxel representation and compare the lists of voxels.

Monkeys and their voxels.
If these models were arbitrarily oriented along the coordinate axes, they could be scaled to the common size of Bounding Box, then move the origin of local coordinates to its center, render them from six sides and compare sets of images among themselves.

Curvature of surfaces.
In order to achieve rotation invariance, I decided to turn to a spherical coordinate system.
Short description of RCVS
Instead of voxelization and rendering, my method is based on Ray Casting. The model is placed inside the icosahedral spherical polyhedron, rays are casted from its polygons towards the model surface and their lengths are collected in lists.
Lists of these lengths are sorted and compared with each other. Sorting eliminates rotation, since for the same or close in geometry models rays lengths will coincide within the margin of error, but differ in order.


80 и 1280 rays respectively.
Comparison results for Suzanne Monkey models:

Suzanne_lo
Suzanne_lo | 1
Suzanne_lo_rot_rand | 0.9878376875939173
Suzanne_lo_rot_90 | 0.9800766750109137
Suzanne_hi_rot_rand | 0.9761078629585936
Suzanne_hi | 0.9730722945028376
Suzanne_hi_rot_90 | 0.9680325422930756
Skull | 0.7697333228143514
Ceramic_Teapot_rot_rand | 0.6634783235048608
Ceramic_Teapot | 0.6496529954470333
Grenade_MK2 | 0.5275616759076022
Detailed description of RCVS
Step illustrations


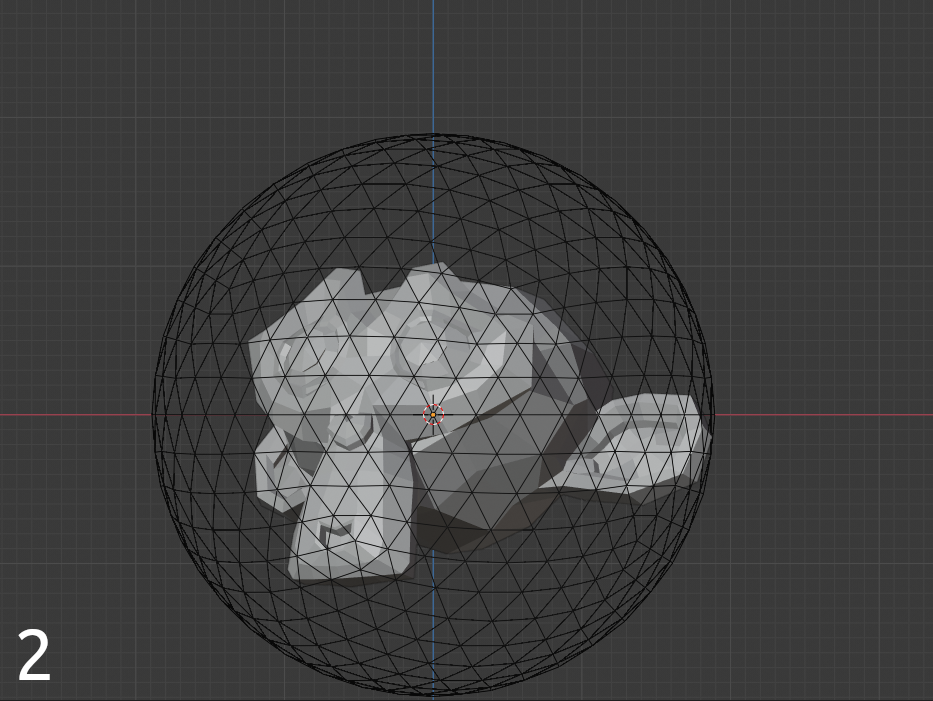



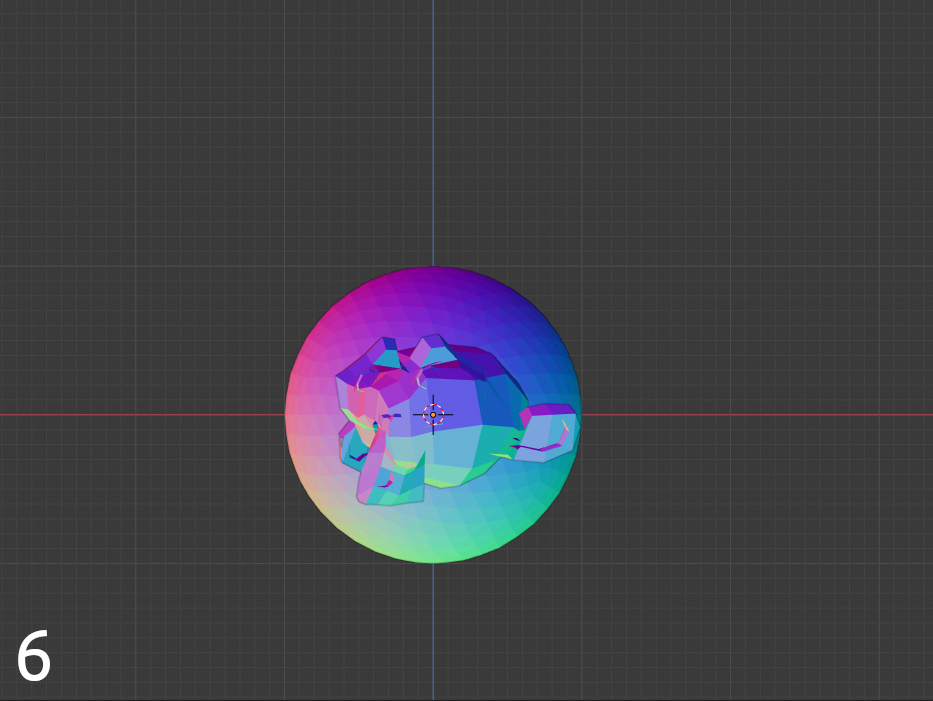







Before comparing 3D models (hereinafter referred to as objects), each one goes through the preparation phase (I implemented this part on Python in Blender):
- The origin of the local coordinates of the components of the object is set at the center of mass from the volume.
- The object fits into the unit sphere centered at the origin of the local coordinates of object components.
- Scale transformations are applied.
- An icosahedral spherical polyhedron (hereinafter referred to as the icosphere) of unit radius with normals directed inward is built around the object. The number of icosphere polygons on which tests were carried out: 80, 320, 1280, 5120, 22480. The optimal number of icosphere polygons by time consumption and accuracy in the tests was determined to be 1280.
- Rays are casted from each polygon of the icosphere towards the object surface with outside facing normals and their lengths are collected in lists.
- Object normals are recalculated to point inside the mesh.
- Rays are casted from each polygon of the icosphere towards the object surface with outside facing normals and their lengths are collected in lists. (This writes the internal geometry and/or fills the blind spots of previous rays).
- Lengths of rays sent from opposite polygons are arranged in lists, where the first two values are from step 5 and the second two are from step 7. Each list is sorted by the smallest length value from step 5 so that the values from steps 5 and 7 match each other in pairs.
- The list of lists of all rays lengths is sorted by the first value. This list has 4 columns and the number of rows equal to half the number of polygons in the icosphere.
- List of rays lengths is written to file.
The list of rays lengths looks something like this:
0.00271218840585662 0.2112752957162676 0.00271218840585662 0.2112752957162676
0.004740002405006037 0.210980921765861 0.004740002405006037 0.2109809188911709
0.00660892842734402 0.2066613370130234 0.00660892842734402 0.2066613370130234
…
0.2692299271137439 0.2725085782639611 0.2692299271137439 0.2725085782639611
0.2705489991382905 0.2707842753523402 0.270548999138295 0.2707843056356914
0.2709498404192674 0.271036677664217 0.2709498404192674 0.271036642944409When all the objects got their lists of rays lengths they can be compared (I wrote this part on Rust):
- Setting the threshold value of the acceptable error. In the tests, the best value was determined to be 0.01, the error within 1%.
- Creating the compliance score variable.
- For each row in the first list, searching for a row from the second, for which the sum of deviations does not exceed the error multiplied by the number of values. If such a string is found, it is not involved in further search. The pairwise absolute difference of the values from the two lists is calculated and subtracted from 1, the arithmetic mean of these values is added to the score.
- When all the lines of the first list are passed, the score value is divided by the number of lines. The calculated value is the result of a comparison.
- If the objects are similar in shape (regardless of their scale and rotation), the result is close to 1.
Bananas, Vitruvian Man, and restrictions of RCVS
The algorithm works great for finding objects close in geometry, for example, high- and low-polygon variants of the same model, sometimes it copes well with objects that are similar in meaning, for example, with teapots or guitars of various shapes. However, since the number of models to which the same list of rays lengths will correspond can be approximately estimated at
To refine search should take into account the size and / or rotation of objects.
Sources
Pyhton code for creating dictionaries of opposite polygons of icospheres in Blender.
import bpy
import os
name = bpy.context.active_object.data.name
polys = bpy.data.meshes[name].polygons
print("-----")
length = len(polys)
x = 0
p = 0
dict = []
for i in range(0, length):
print(i, "/", length)
for l in range(i, length):
norm1 = polys[i].normal
norm2 = polys[l].normal
if norm1 == -norm2:
dict.append(str(i)+", "+str(l))
p += 1
print("Polys", p)
basedir = os.path.dirname(bpy.data.filepath) + "/ico_dicts/"
if not os.path.exists(basedir):
os.makedirs(basedir)
file = open(basedir + "/" + str(length) + ".csv","w")
for poly in dict:
file.write(poly + "\n")
file.close()
print("----ok----")
Python code for batch preparation of objects and calculating the lists of rays lengths in Blender.
import bpy
import os
from math import sqrt
import csv
#Icosphere properties
#icosubd:
#5 -> 5120 X 2 rays
#4 -> 1280 X 2 rays
#3 -> 320 X 2 rays
#2 -> 80 X 2 rays
icosubd = 4
size = 1280 #name of directory
radius = 1
def icoRC(icosubd, rad, raydist, normals, target):
icorad = rad
bpy.ops.mesh.primitive_ico_sphere_add(radius=icorad, subdivisions=icosubd, enter_editmode=True, location=(0, 0, 0))
bpy.ops.mesh.normals_make_consistent(inside=normals)
bpy.ops.object.editmode_toggle()
ico = bpy.context.active_object
mesh = bpy.data.meshes[ico.data.name]
rays = []
size = len(mesh.polygons)
for poly in mesh.polygons:
normal = poly.normal
start = poly.center
ray = target.ray_cast(start, normal, distance=raydist)
if ray[0] == True:
length = sqrt((start[0]-ray[1][0]) ** 2 + (start[1]-ray[1][1]) ** 2 + (start[2]-ray[1][2]) ** 2)
rays.append(length / (radius *2))
else:
rays.append(-1)
result = []
#Combine opposite rays using CSV dicts
dictdir = os.path.dirname(bpy.data.filepath) + "/ico_dicts/"
with open(dictdir+str(size)+'.csv', newline='') as csvfile:
ico_dict_file = csv.reader(csvfile, delimiter=',')
for row in ico_dict_file:
result.append([rays[int(row[0])], rays[int(row[1])]])
bpy.ops.object.select_all(action='DESELECT')
bpy.data.objects[ico.name].select_set(True)
bpy.ops.object.delete()
return result
#Batch preparation of objects by scale and origin
def batch_prepare():
for obj in bpy.context.selected_objects:
bpy.ops.object.origin_set(type='ORIGIN_CENTER_OF_VOLUME', center='MEDIAN')
max_dist = 0
bb = bpy.data.objects[obj.name].bound_box
for vert in obj.data.vertices:
dist = vert.co[0]**2 + vert.co[1]**2 + vert.co[2]**2
if dist > max_dist:
max_dist = dist
obj.scale *= (1 / sqrt(max_dist))
def write_rays(dir):
for obj in bpy.context.selected_objects:
bpy.ops.object.transform_apply(location=False, rotation=False, scale=True)
#Cast rays on object with normals turned inside
bpy.context.view_layer.objects.active = obj
bpy.ops.object.editmode_toggle()
bpy.ops.mesh.normals_make_consistent(inside=True)
bpy.ops.object.editmode_toggle()
result1 = icoRC(icosubd, radius, radius*2, True, obj)
#Cast rays on object with normals turned outside
bpy.context.view_layer.objects.active = obj
bpy.ops.object.editmode_toggle()
bpy.ops.mesh.normals_make_consistent(inside=False)
bpy.ops.object.editmode_toggle()
result2 = icoRC(icosubd, radius, radius*2, True, obj)
final = []
#Sort sub-lists and append them to main list
for i in range(0, len(result1)):
if result2[i][0] < result2[i][1]:
final.append([result2[i][0], result2[i][1], result1[i][0], result1[i][1]])
else:
final.append([result2[i][1], result2[i][0], result1[i][1], result1[i][0]])
basedir = os.path.dirname(bpy.data.filepath) + "/rays/" + str(size) + "/"
if not os.path.exists(basedir):
os.makedirs(basedir)
file = open(basedir + "/" + obj.name,"w")
final.sort(key=lambda x: x[0]) #Sort list by first values in sub-lists
#Writing to file
for ray in final:
ray_str = ""
for dist in ray:
ray_str += str(dist) + " "
file.write(ray_str + "\n")
file.close()
batch_prepare()
write_rays(size)
Rust code for lists comparison.
use rayon::prelude::*;
use std::collections::HashSet;
use std::fs;
use std::io::{BufRead, BufReader, Error, Read};
//Creates Vector from file
fn read<R: Read>(io: R) -> Result<Vec<Vec<f64>>, Error> {
let br = BufReader::new(io);
br.lines()
.map(|line| {
line.and_then(|v| {
Ok(v.split_whitespace()
.map(|x| match x.trim().parse::<f64>() {
Ok(value) => value,
Err(_) => -1.0,
})
.collect::<Vec<f64>>())
})
})
.collect()
}
//Compares two objects
fn compare(one: &Vec<Vec<f64>>, two: &Vec<Vec<f64>>, error: f64) -> f64 {
let length = one.len();
let mut count: f64 = 0.0;
let mut seen: HashSet<usize> = HashSet::new();
for orig in one {
let size = orig.len();
for i in 0..length {
if seen.contains(&i) {
continue;
} else {
let targ = &two[i];
if (0..size).map(|x| (orig[x] - targ[x]).abs()).sum::<f64>() > error * size as f64 {
continue;
}
let err_sum = (0..size)
.map(|x| 1.0 - (orig[x] - targ[x]).abs())
.sum::<f64>();
count += err_sum / size as f64;
seen.insert(i);
break;
}
}
}
count / length as f64
}
//Compares one object with others on different threads
fn one_with_others(
obj: &(String, Vec<Vec<f64>>),
dict: &Vec<(String, Vec<Vec<f64>>)>,
) -> Vec<(usize, f64)> {
let length = dict.len();
(0..length)
.into_par_iter()
.map(|x| {
println!("Puny human is instructed to wait.. {:}/{:}", x + 1, length);
(x, compare(&obj.1, &dict[x].1, 0.01))
})
.collect()
}
fn main() {
let ray = 1280; //name of directory
let obj_cur = "Suzanne_lo"; //name of object
let mut objects = Vec::<(String, Vec<Vec<f64>>)>::new();
let path_rays = format!("./rays/{:}/", ray);
let paths = fs::read_dir(path_rays).unwrap();
let obj_path = format!("./rays/{:}/{:}", ray, obj_cur);
let obj = (
obj_cur.to_string(),
read(fs::File::open(obj_path).unwrap()).unwrap(),
);
for path in paths {
let dir = &path.unwrap().path();
let name = dir.to_str().unwrap().split("/").last().unwrap();
objects.push((
name.to_string(),
read(fs::File::open(dir).unwrap()).unwrap(),
));
}
let mut result = one_with_others(&obj, &objects);
result.sort_by(|a, b| b.1.partial_cmp(&a.1).unwrap());
print!("{}\n", "_".repeat(150));
println!("{:}", obj.0);
for line in result {
println!(
"{:>36} |{:<100}| {:<14}",
objects[line.0].0,
"▮".repeat((line.1 * 100.0).round() as usize),
line.1
);
}
}