
Есть довольно простая идея, высказанная Фейнманом — цель физики найти простейшую теорию, которая сможет объяснить как можно больше явлений природы. Эта та идея, которая стоит за электродинамикой Максвелла или КЭД. Каждая новая большая теория объясняла больше явления природы и при этом была проще предшественников.
Это довольно простая мысль с далеко идущими последствиями. Так почему бы нам (инженерам) не взять ее на вооружение? Почему одни из лучших идей про разработку еще не формализованы и унифицированы, как тот же KISS или DRY? Они что, по сути не формализуемы? Это не может быть так если мы возьмем во внимание тот факт что информатика это раздел математики. Должен быть какой-то способ вывести эти пресловутые лучшие практики. И может, если у нас получиться вывести те что мы знаем по опыту, мы сможем выводить совершенно новые. В других научных дисциплинах именно это и происходило — ярче всего это было в авиации. Сначало, опытным путем, инженерам получилось построить то что хоть как-то да отрывается от земли, и только после физика крыла реально была изучена. С этой новой физикой мы имели просто взрывной рост отрасли.
Эта статься — моя приближенная попытка потыкать это все в поисках наших лучших практики в очень упрощенной математике стоящей за информатикой. Я предполагаю, все хорошо сформированные лучшие практики выводимы.
Категории
Одной из простых математических формалистик программирования является теория категорий. Причем, самые ее простые части. В попытке найти формализации для лучших практик я предлагаю посмотреть на теорию категорий как на интересный и понятный пример. Чтобы углубиться нам потребуется чуть-чуть освежить знания по тому что и как с этими категориями.
Теория категорий это про коллекцию объектов связанных стрелочками.
Вообще, в программировании нас интересует специальная категория — категория типов. В ней объектами являются типы а стрелками являются функции связывающие их.
В этом, очень простом определении, мы можем сделать наблюдение, что все интересное находится в функциях. Типы нужны, чтобы связать функции, чтобы у функции были начала и конец. В общем случае, нас даже не интересует как много функций есть между объектами — 1, 2, или бесконечность.
Второе то, что нам нужно для нашего рудиментарного анализа — это композиция.
Композиция
В теории категорий, композиция это способность установления прямых связей между двумя объектами, если эти объекты уже как-то да связаны.

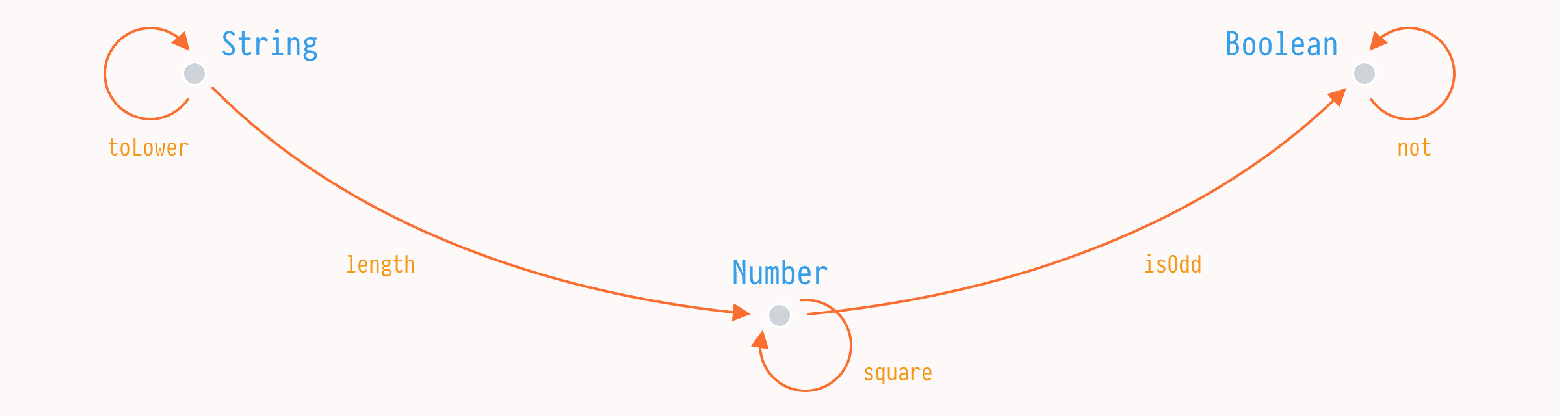
Если у нас есть функции length и isOdd между String, Number, и Boolean, то мы можем их связать эти объекты новой функцией isOdd ◦ length. Это, в общем, почти все, ну разве что есть пара простых правил.
length ◦ isOdd != isOdd ◦ length
length ◦ toLower = lengthНу, хорошо, к этому моменту у нас есть какие-то зачатки формализации программирования, вы наверное, даже можете видеть какое-то сходство с функциональными языками. Но это просто из-за нотации — все это также справедливо и для императивого стиля.
Keep it simple, stupid
Или KISS. Моя проблема с этой лучшей парктикой в пулл реквестах, чатах, да просто в разговорах в курилке была в том, что все блин понимают этот simple (просто) по-разному. На это мы и попробуем обратить наш взор — можно ли что-то дельное сказать о простоте? И кажется, что да.
Для начала, давайте представим простое приложение с пятью типами и четырьмя функциями их связывающими.

f: A -> B
g: A -> C
k: A -> E
h: C -> DВ этой маленькой программе у нас есть одна точка входа (A) и возможность пройтись от нее к другим с помощью f, g, h, и k. Но это не все, мы можем даже сделать лучше и связать A и D напрямую композируя h и g.

h ◦ g: A -> DВ каком-то смысле, мы получили h ◦ g за так. И теперь можем отобразить A к D когда и если необходимость появится. Скажем в следующем спринте, когда менеджер продукта захочет показать инвойсы (D) пользователя (A) по транзакциям (C).
Но есть вопрос, можно ли написать эту несчастную программу как-то еще лучше? Так, чтобы когда менеджер продукта придет, нам пришлось делать еще меньше изменений? И ответ на этот вопрос — да.
Скажем, мы начнем с тех же типов и с того количества функций, но немного в другой конфигурации.

f: A -> B
m: B -> C
l: C -> E
h: C -> DМы заменили g и k из прошлого примера на m и l и при первом приближении потеряли отображение от A к C и A к E соответсвенно. Но у нас же есть композиция.
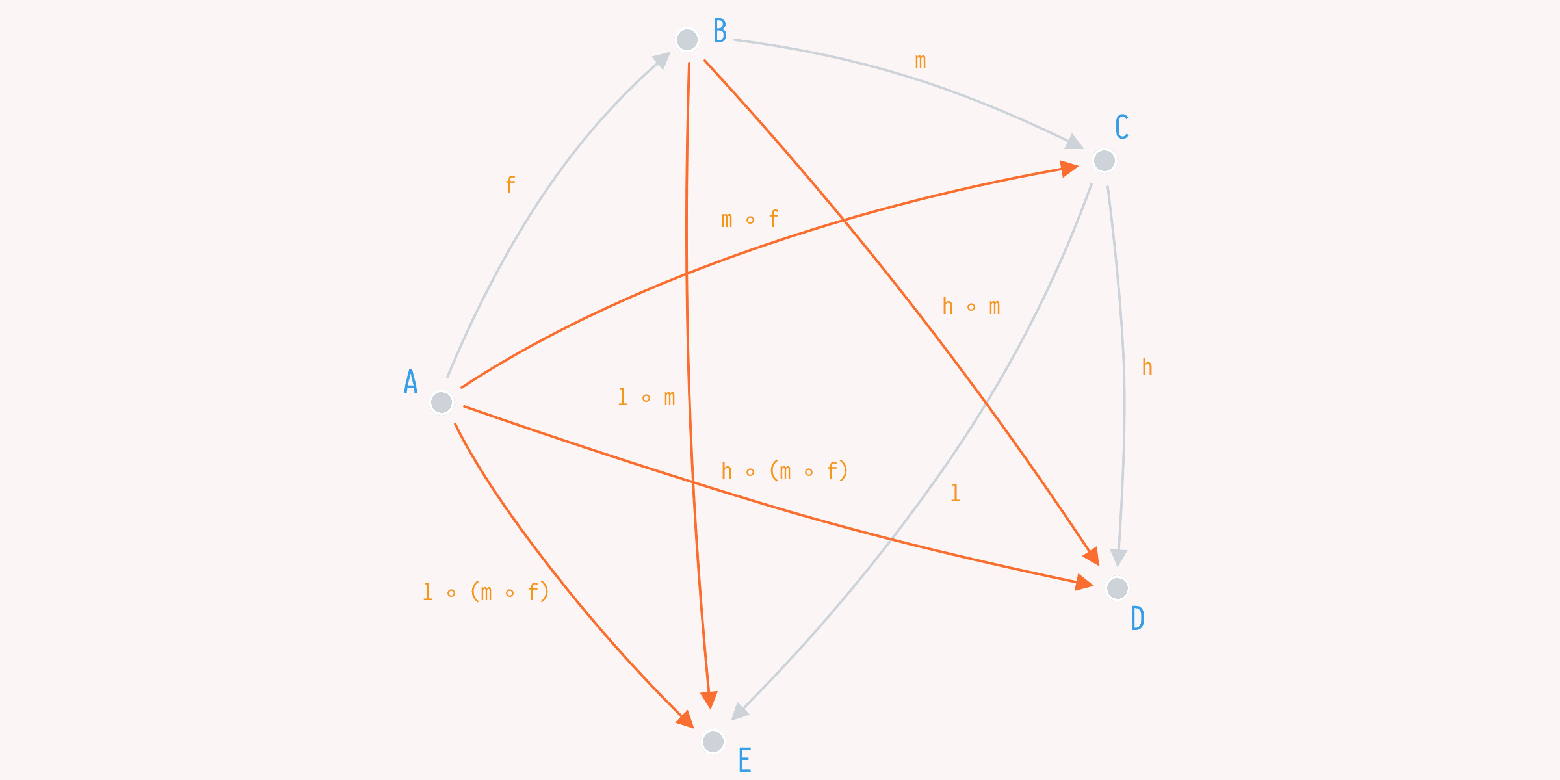
То же число изначальных функций на тех же типах дает нам аж 5 (!) новых функций. Это на 4 больше чем, что у нас было в прошлый раз.
m ◦ f: A -> C
h ◦ m: B -> E
l ◦ m: B -> D
l ◦ (m ◦ f): A -> E
h ◦ (m ◦ f): A -> DБолее того, мы получили наши g и k обратно через композицию. g стала m ◦ f, а k стала l ◦ (m ◦ f).
Этот пример показывает кое-что интересное. Некоторые функции легче композировать чем другие. В приложений будут функции которые легче композируются с другими функциями в этом приложении для получения новых возможностей. И это именно то, как можно определить простоту.
Простые функции в заданном приложении — это те функции, которые можно композировать большим количеством способов, чем другие.
Это определение интересно не только тем что говорим нам о том что просто в KISS, но и говорит что простота относительна для каждого заданного приложения. Что это значит на самом деле? Если вы можете написать функцию a такую что через композицию с другими функциями в заданном приложении мы можем получить, скажем, 10 новых функции. Или, вы можете написать две функции b и c, которые через композицию могут дать, скажем, 20 новых. То, в общем случае, две функции b и c проще одной a.
Что дальше?
Изначально я думал про DRY и пришел к выводу что она по сути дела про бета-эквивалентность. Попробую написать об этом следующий раз.
Я приглашаю вас потыкать эти кусочки информатики, там точно есть возможность формализовать и простить наш эмпирический опыт. Это как минимум поможет лучше разобраться для себя что к чему.