Картинка для привлечения внимания:

Внимание! Под катом много картинок!

В этой статье будет описано проектирование и создание однобитного компьютера. Всем кто заинтересовался, добро пожаловать под кат.

Мы нашли все самые крутые логические задачи!

15 лет назад мы решили создать сайт для любителей каверзных задач и головоломок. Не просто сборник с ответами под катом, а интерактивный ресурс, дающий возможность насладиться самостоятельным поиском решения, почувствовать озарение, научиться смотреть на вещи под другим углом и поверить в свои силы. 

Так появилось сообщество решателей задач BrainGames.ru. Наш сайт развивался и менялся, сменялись решающие, сменялись проверяющие, но вот уже много лет мы не изменяем трем основным принципам: 

Мы не даем ответов. Ответ узнать можно, но только найдя его самостоятельно и услышав “верно” от модератора (так мы называем проверяющих задачи).

Задачи проходят жесткий отбор и переработку. 

Присоединиться к сообществу и проверить ответ смогут только те, кто решит несколько “регистрационных” задач - простых, но нестандартных. 

Автор: Forbidden World

Думаете, что и так знаете про успехи США, Германии и особенно Великобритании в области криптографии?

“Я же смотрел “Игру в имитацию”!” - распространенный комментарий, распространенное заблуждение. Все было не так, как показали в кино. Британцы были не самые умные, Алан Тьюринг не был самым успешным в дешифровальной службе, а США не полагались только на своих союзников. Ну и британский компьютер, который вы видите ниже на картинке, НИКАК не связан с Тьюрингом.

А материал об успехе дешифровальной службы Германии впервые переведен на русский язык для этой статьи. Пришло время срывать покровы, интересно узнать как оно было на самом деле?

Часть 1

Добро пожаловать под кат!

Автор: Forbidden World

Еще одна статья про взлом Энигмы?! Конечно нет, мы поговорим обо ВСЕХ шифровальных машинах, активно использовавшихся во Второй Мировой Войне, и, конечно же, поговорим о том, как их пытались взломать.

Радиоперехват стал известен с Первой мировой войны, поэтому ко второй мировой все страны-участники подготовились основательно, поэтому и бои на криптофронте были не менее ожесточенными.

Япония, СССР, Великобритания, США и Германия. В этой и следующей статье рассмотрим атаку и защиту каждой страны, ответим и на нестандартные вопросы:

— Почему шифровальщики носили с собой взрывчатку?

— Почему в армии США ценили коренных американцев?

— Как сводки погоды, минные поля и нацистские приветствия помогали союзникам?

— Почему СССР даже не пытался взломать шифровальные машины Германии?

— И почему математически идеальный шифр все равно расшифровывали?

— Интересно? Тогда добро пожаловать под кат!

Китайская фантастика и ее успехи за границами Поднебесной неразрывно связана с именем Лю Цысиня, однако его творчеством не ограничивается. После того, как «Задача трех тел» стала бестселлером на Западе и завоевала «Хьюго», издатели стали обращать внимание и на других китайских фантастов. Одним из них сталь Чэнь Цюфань, чей роман «Мусорный прибой» — эдакий киберпанк по-китайски — куда более приземленный и приближенный к реальности, чем эпическая сага Цысиня.

Недавно на Wired вышла большая статья про Цюфаня. Интересна она в частности тем, что рассказывает не только о самом писателе, но и о том месте, которое фантастика и ее авторы сейчас занимают в Китае. Это, по-моему, весьма любопытно, поэтому перевел материал.

Появившиеся в C++11 лямбды стали одной из самых крутых фич нового стандарта языка, позволив сделать обобщённый код более простым и читабельным. Каждая новая версия стандарта C++ добавляет новые возможности лямбдам, делая обобщённый код ещё проще и читабельнее. Вы заметили, что слово «обобщённый» повторилось дважды? Это неспроста – лямбды действительно хорошо работают с кодом, построенным на шаблонах. Но при попытке использовать их в необобщённом, построенном на конкретных типах коде, мы сталкиваемся с рядом проблем. Статья о причинах и путях решения этих проблем.

Последний год я собирал различные клавиатуры, что включает в себя и написание прошивок под различные управляющие схемы.

Первоначально, я писал их на Rust, но несмотря на годы опыта разработки на нем, приходилось повоевать. Со временем, я заставил мои клавиатуры работать, но это заняло неприличное количество времени и не приносило мне удовольствия.

После неоднократных предложений от моего более подкованного в Rust-и-вычислительной технике друга Джейми Брэндона, я переписал прошивку на Zig, и вышло очень удачно.

Я нашел это поразительным, учитывая, что я никогда не видел Zig раньше, и этот язык, еще даже не версии 1.0, созданный хипстером из Университета Портленда, и описывается, по сути, всего одной страницей документации.

В настоящий момент появилось достаточно большое количество библиотек дополненной реальности с богатым функционалом (ARCore, ARKit, Vuforia). Тем не менее я решил начать свой открытый проект, попутно описывая как это работает изнутри. Если повезет, то позже получится добавить какой-то особый интересный функционал, которого нет в других библиотеках. В качестве целевых платформ пока возьмем Windows и Android. Библиотека пишется на C++, и сторонние библиотеки будут задействованы по минимуму, т.е. преимущественно не будет использовано ничего готового. Фокус в статьях будет направлен на алгоритмы и математику, которые постараюсь описать максимально доступно и подробно. В этой статье пойдет речь про основы векторной алгебры.

Как пишут тексты в Большой Академии в Лагадо

Алгебра и язык (письменность) являются двумя разными инструментами познания. Если их объединить, то можно рассчитывать на появление новых методов машинного понимания. Определить смысл (понять) – это вычислить как часть соотносится с целым. Современные поисковые алгоритмы уже имеют задачей распознавание смысла, а тензорные процессоры Google выполняют матричные умножения (свертки), необходимые для алгебраического подхода. При этом в семантическом анализе используются в основном статистические методы. В алгебре выглядело бы странным использование статистики при поиске, например, признаков делимости чисел. Использование алгебраического аппарата полезно также для интерпретации результатов вычислений при распознавании смысла текста.

Директор DataArt Armenia Арсен Багдасарян 25 лет назад начинал системным администратором. Продолжил тестировщиком, дойдя до руководства QA-департаментом в армянском представительстве Synopsys, затем перешел в аутсорсинг. Вместе с Арсеном мы выбрали несколько историй из его жизни, которые иллюстрируют формирование рынка IT в постсоветской Армении. 

Рассказ Арсена Багдасаряна хронологически завершает большой цикл интервью, посвященных истории армянской вычислительной техники, которые музейный проект DataArt собирал более года. В ближайшем будущем мы откроем отдельный лендинг об Армении на сайте IT-музея DataArt.

Сколтех провел марафон хакатонов для своих студентов — Hack Lab. Хакатоны проходили онлайн на английском языке.

Два хакатона курировал Тинькофф: студенты обучали ассистента Олега новым навыкам. Задача была пересмотреть стереотип о том, что тема финансов сложная и скучная.

За выходные ребята придумали больше 20 идей для игр с Олегом: квесты, викторины, квизы и соревнования. Некоторые идеи Тинькофф взял в разработку.

Для того, чтобы упростить написание и чтение кода, программисты периодически придумывают всякие техники. Об одной из таких техник я уже писал в публикации Долой циклы, или Неленивая композиция алгоритмов в C++.

Однако есть и классическая, более распространённая техника для борьбы с циклами — использование итераторов и диапазонов для ленивых операций над последовательностями. Всё это уже сто лет есть в Бусте и других сторонних библиотеках (к примеру, range-v3) и постепенно просачивается в стандартную библиотеку.

Хотя, в некотором смысле, и в стандартной библиотеке ленивые итераторы уже есть давно (см. std::reverse_iterator).

Данная публикация — это краткий ликбез о том, что такое ленивые итераторы и диапазоны, зачем они нужны и как ими пользоваться.

В C++ нет понятия "множество". Есть std::set, но это всё-таки конкретный контейнер. Есть функции для работы с упорядоченными диапазонами: merge, inplace_merge, includes, set_difference, set_intersection, set_symmetric_difference, set_union, но это алгоритмы, они не ленивые, и при вызове сразу вычисляют результат. К тому же они предназначены для работы строго с двумя диапазонами.

Что же делать, если, во-первых, диапазонов много (больше двух), а во-вторых, мы хотим вычислять результат не сразу, а по необходимости?

В данной публикации я хочу показать, как спроектировать ленивый диапазон, который будет производить какую-либо операцию с N множествами.

В публикации Ленивые итераторы и диапазоны в C++ я разбирал, что такое ленивые диапазоны.

Техника безопасности при работе с макросами в C и C++.

Можно ли сделать решение дифференциальных уравнений увлекательным, а результаты яркими и красочными? Вот к чему могут привести многолетние усилия в этом направлении

В данной статье мы расскажем о том, что такое внешняя алгебра, и для чего она нужна. Удивительно, но на Хабре почти нет статей о внешней алгебре при том, что ее прикладная ценность ничуть не меньше, например, реляционной алгебры.

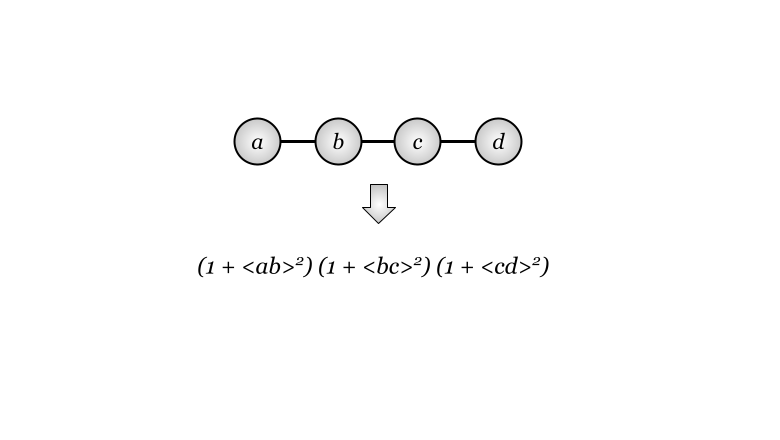
Наше описание отличается от традиционного изложения в учебниках тем, что мы хотим наполнить внешнюю алгебру прежде всего информатикой, а не геометрией или физикой. Конечная цель статьи - представить произвольный граф в виде алгебраического выражения и показать, что свойства графа можно вычислять как свойства данного выражения. На пути к этому мы познакомимся с основными идеями внешней алгебры.

В данной работе мы продолжаем обзор свойств внешней алгебры. В первой части мы определили внешнее произведение элементов, ввели понятие симплексов, границ и копространства. Здесь рассмотрим аффинные пространства, в которых определено скалярное произведение между элементами, их называют также евклидовыми.

Обычно в качестве примера евклидового приводят окружающее нас трехмерное пространство. В нем действительно есть скалярное произведение между элементами и векторами. Но все-таки оно является лишь частным случаем общего семейства евклидовых пространств. Более общим примером являются пространства со связями, в простонародье именуемые графами. Поэтому в основном на метрических свойствах графах мы и сосредоточимся, а в конце покажем, как от графов перейти к обычному пространству.

Похоже, что во второй части я сделал слишком большой шаг и положил на лопату слишком много. Тут тебе и формы с полиформами, и границы, и графы, и пространства с метрикой... Средний читатель Хабра напрягся ). Поэтому я решил дописать промежуточную часть, которую по-хорошему надо вставить между первой и второй.

Здесь мы сделаем только один шаг - проведем мостик между внешним произведением и формами, покажем связь форм и тензоров. Прикладной аспект продемонстрируем на простейшей задаче определения неизвестных характеристик объекта по известным.