Недавно на Хабре появилась удивительная статья «Папа, а почему на ноль делить нельзя?», которая собрала массу не менее удивительных комментариев.

Детские вопросы обычно очень сложны («Почему небо ночью темное?», «Почему яблоки падают на землю?») и у взрослых обычно не хватает времени, чтобы их доходчиво объяснить. Да и не всегда взрослые знают ответ на эти вопросы.

Однако, вопрос о делении на ноль ни разу не относится к числу сложных вопросов, и для меня остается загадкой, почему с ним возникает столько проблем. Наверное, виной тому какие-то изъяны в методике преподавания математики в средней школе, в трудностях перехода от изучения арифметики к изучению буквенной алгебры и свойств элементарных функций.



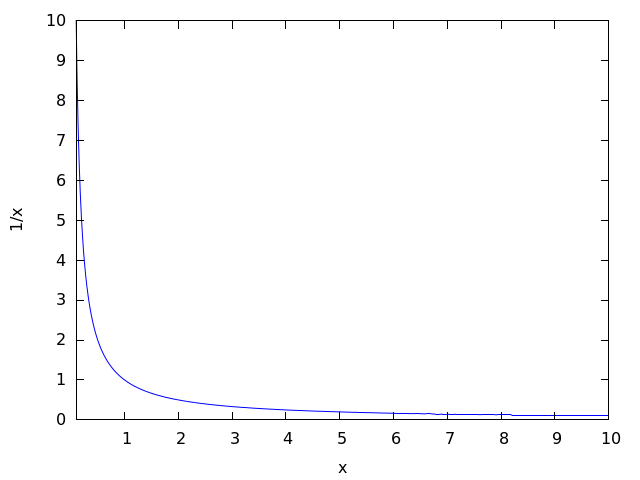
Самые серьезные сомнения появляются, я думаю, после изучения рациональных чисел, когда для любого числа x, кроме нуля, вводится понятие обратного числа 1/x, и графика гиперболы y(x)=1/x.

Очевидно, что при делении 1 на очень маленькие числа появляются очень большие числа, и чем меньше мы берем x, тем больше становится 1/x. Почему же мы не можем сказать, что 1/x=∞ — есть некоторое число?

Алгебраическое возражение против этого состоит в следующем. Предположим, что ∞=1/x является числом. Тогда на это число должны распространяться все правила, которые имеют место быть для обычных чисел. В частности, с одной стороны должно быть верно соотношение 0⋅∞=1, а с другой стороны поскольку 0=1−1 должно быть выполнено 0⋅∞=1⋅∞−1⋅∞=0. Таким образом, имеем 1=0, а из этого уже следует, что все числа равны между собой и равны нулю. В самом деле, поскольку для любого числа x верно 1⋅x=x, то 1⋅x=0⋅x=0.

«Ну разве это не полная чушь?» — спросим себя, добравшись до этого места.

Разумеется, это полная чушь, если мы говорим об обычных числах. Но я недаром подчеркнул выше слово «правила». К ним мы вернемся чуть позже, после рассмотрения арифметического возражения против деления на ноль, и поможет нам в этом фасоль.

Вернемся в те времена, когда не было ни компьютеров, ни калькуляторов, ни логарифмических линеек, и поставим перед собой задачу разделить некоторое случайное число, например, на 5.

Для этого берем чашу с фасолью, символизирующую натуральный ряд, и высыпаем из нее какое-то количество зерен на разлинованный лист бумаги:



Тем самым, мы установили делимое на нашем бобовом калькуляторе.