В прошлый раз я рассказал, пока в самых общих чертах, о сингулярном разложении – главном инструменте современной коллаборативной фильтрации. Однако в прошлый раз мы в основном говорили только об общих математических фактах: о том, что SVD – это очень крутая штука, которая даёт хорошие низкоранговые приближения. Сегодня мы продолжим разговор об SVD и обсудим, как же, собственно, использовать всю эту математику на практике.
И снова начнём издалека: посмотрим на то, из чего будет складываться рейтинг одного продукта. Во-первых, вполне может быть, что пользователь добрый и всем подряд выдаёт хорошие рейтинги; или, наоборот, злой и рейтинг зажимает. Если не учесть этот базовый фактор, ничего не получится – без поправки на среднее рейтинги разных пользователей не сравнить. С другой стороны, некоторые продукты попросту лучше других (или хотя бы раскручены лучше), и это тоже следует учитывать аналогичным образом.
Поэтому мы начнём с того, что введём так называемые базовые предикторы (baseline predictors)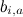
, которые складываются из базовых предикторов отдельных пользователей 
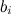и базовых предикторов отдельных продуктов 
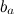, а также просто общего среднего рейтинга по базе μ:
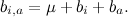
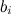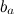Если мы захотим найти только базовые предикторы, мы должны будем найти такие μ, и , для которых 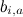лучше всего приближают имеющиеся рейтинги.
Затем можно будет добавить собственно факторы – теперь, когда мы сделали поправку на базовые предикторы, остатки будут сравнимы между собой, и можно будет надеяться получить разумные факторы:
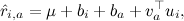
где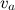
– вектор факторов, представляющий продукт a, а 
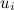– вектор факторов, представляющий пользователя i.
Может показаться, что найти, например, базовые предикторы – дело совсем простое: давайте просто подсчитаем средний рейтинг по всей базе
, примем его за μ, потом вычтем его из каждой оценки и подсчитаем средние рейтинги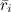 
по пользователям и 
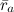по продуктам. Однако считать эти предикторы таким образом было бы неправильно: на самом деле они зависят друг от друга, и оптимизировать их надо вместе.
Теперь мы можем вернуться к исходной задаче и сформулировать её точно: нам нужно найти наилучшие предикторы, которые приближают
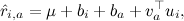
Что здесь значит «наилучшие»? Первое приближение к ответу на этот вопрос звучит так: «наилучшие» – это те, которые меньше всего ошибаются на имеющихся данных. Как определить ошибку? Можно, например, сложить квадраты отклонений (кстати, почему именно квадраты? об этом мы тоже ещё поговорим в следующих сериях) у тех рейтингов, которые мы уже знаем:
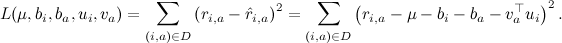
А как минимизировать такую функцию? Да очень просто – градиентным спуском: берём частные производные по каждому аргументу и двигаемся в сторону, обратную направлению этих частных производных. Функция ошибки – квадратичная поверхность, так что никаких сюрпризов нас здесь не ждёт.
Однако если мы теперь выпишем и реализуем формулы для градиентного спуска по полученной функции ошибки L, практический результат на реальных датасетах нас вряд ли обрадует. Чтобы обучить хорошие значения предикторов и факторов, нам, вообще говоря, неплохо было бы разобраться в других важных концепциях машинного обучения – оверфиттинге и регуляризации, и в одной из следующих серий мы увидим это на практике. А пока просто поверьте, что нужно ещё штрафовать за слишком большие значения обучаемых переменных; например, можно просто добавить в функцию ошибки сумму квадратов всех факторов и предикторов.
В результате функция ошибки выглядит как
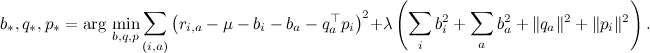
где λ – параметр регуляризации.
Если взять у неё частные производные по каждой из оптимизируемых переменных, получим простые правила для (стохастического) градиентного спуска:
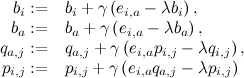
для всех j, где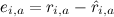
– ошибка на данном тестовом примере, а γ – скорость обучения. Эта модель называется SVD++, и именно она легла в основу модели-победительницы в Netflix Prize (хотя, конечно, она не могла выиграть в одиночку – о том, почему так и что же делать, мы тоже ещё поговорим позже).
В следующий раз я попробую разобрать конкретный пример: применить SVD к матрице предпочтений, проанализировать, что получается, выделить основные трудности. Надеюсь, будет интересно!
И снова начнём издалека: посмотрим на то, из чего будет складываться рейтинг одного продукта. Во-первых, вполне может быть, что пользователь добрый и всем подряд выдаёт хорошие рейтинги; или, наоборот, злой и рейтинг зажимает. Если не учесть этот базовый фактор, ничего не получится – без поправки на среднее рейтинги разных пользователей не сравнить. С другой стороны, некоторые продукты попросту лучше других (или хотя бы раскручены лучше), и это тоже следует учитывать аналогичным образом.
Поэтому мы начнём с того, что введём так называемые базовые предикторы (baseline predictors)
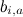, которые складываются из базовых предикторов отдельных пользователей 
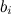и базовых предикторов отдельных продуктов 
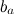, а также просто общего среднего рейтинга по базе μ: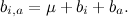
Если мы захотим найти только базовые предикторы, мы должны будем найти такие μ,
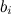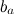и , для которых 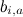лучше всего приближают имеющиеся рейтинги.Затем можно будет добавить собственно факторы – теперь, когда мы сделали поправку на базовые предикторы, остатки будут сравнимы между собой, и можно будет надеяться получить разумные факторы:
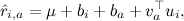
где
– вектор факторов, представляющий продукт a, а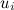 
– вектор факторов, представляющий пользователя i.Может показаться, что найти, например, базовые предикторы – дело совсем простое: давайте просто подсчитаем средний рейтинг по всей базе
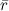, примем его за μ, потом вычтем его из каждой оценки и подсчитаем средние рейтинги 
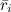по пользователям и 
по продуктам. Однако считать эти предикторы таким образом было бы неправильно: на самом деле они зависят друг от друга, и оптимизировать их надо вместе.Теперь мы можем вернуться к исходной задаче и сформулировать её точно: нам нужно найти наилучшие предикторы, которые приближают
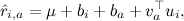
Что здесь значит «наилучшие»? Первое приближение к ответу на этот вопрос звучит так: «наилучшие» – это те, которые меньше всего ошибаются на имеющихся данных. Как определить ошибку? Можно, например, сложить квадраты отклонений (кстати, почему именно квадраты? об этом мы тоже ещё поговорим в следующих сериях) у тех рейтингов, которые мы уже знаем:
А как минимизировать такую функцию? Да очень просто – градиентным спуском: берём частные производные по каждому аргументу и двигаемся в сторону, обратную направлению этих частных производных. Функция ошибки – квадратичная поверхность, так что никаких сюрпризов нас здесь не ждёт.
Однако если мы теперь выпишем и реализуем формулы для градиентного спуска по полученной функции ошибки L, практический результат на реальных датасетах нас вряд ли обрадует. Чтобы обучить хорошие значения предикторов и факторов, нам, вообще говоря, неплохо было бы разобраться в других важных концепциях машинного обучения – оверфиттинге и регуляризации, и в одной из следующих серий мы увидим это на практике. А пока просто поверьте, что нужно ещё штрафовать за слишком большие значения обучаемых переменных; например, можно просто добавить в функцию ошибки сумму квадратов всех факторов и предикторов.
В результате функция ошибки выглядит как
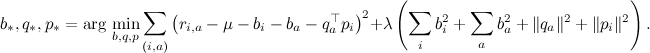
где λ – параметр регуляризации.
Если взять у неё частные производные по каждой из оптимизируемых переменных, получим простые правила для (стохастического) градиентного спуска:
для всех j, где
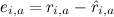– ошибка на данном тестовом примере, а γ – скорость обучения. Эта модель называется SVD++, и именно она легла в основу модели-победительницы в Netflix Prize (хотя, конечно, она не могла выиграть в одиночку – о том, почему так и что же делать, мы тоже ещё поговорим позже).В следующий раз я попробую разобрать конкретный пример: применить SVD к матрице предпочтений, проанализировать, что получается, выделить основные трудности. Надеюсь, будет интересно!
