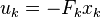Пара часов из жизни математика-программиста или читаем википедию
Для начала в качестве эпиграфа цитирую rocknrollnerd:
— Здравствуйте, меня зовут %username%, и втайне раскрываю суммы из сигма-нотации на листочке, чтобы понять, что там происходит.
— Привет, %username%!
Итак, как я и говорил в своей прошлой статье, у меня есть студенты, которые панически боятся математики, но в качестве хобби ковыряются паяльником и сейчас хотят собрать тележку-сигвей. Собрать-то собрали, а вот держать равновесие она не хочет. Они думали использовать ПИД-регулятор, да вот только не сумели подобрать коэффициенты, чтобы оно хорошо работало. Пришли ко мне за советом. А я ни бум-бум вообще в теории управления, никогда и близко не подходил. Но зато когда-то на хабре я видел статью, которая говорила про то, что линейно-квадратичный регулятор помог автору, а пид не помог.
Если ПИД я ещё себе худо-бедно на пальцах представляю (вот моя статья, которую с какого-то перепугу перенесли на гиктаймс), то про другие способы управления я даже и не слышал толком. Итак, моя задача — это представить себе (и объяснить студентам, а заодно и вам), что такое линейно-квадратичный регулятор. Пока что работы с железом не будет, я просто покажу, как я работаю с литературой, ведь именно это и составляет львиную долю моей работы.
Раз уж пошёл эксгибиционизм про мою работу, то вот вам моё рабочее место (кликабельно):


Используемые источники
Итак, первое, что я делаю, иду в википедию. Русская википедия жестока и беспощадна, поэтому читаем только английский текст. Он тоже отвратителен, но всё же не настолько. Итак, читаем. Из всех вводных кирпичей текста только одна фраза меня заинтересовала:
The theory of optimal control is concerned with operating a dynamic system at minimum cost. The case where the system dynamics are described by a set of linear differential equations and the cost is described by a quadratic function is called the LQ problem.
В переводе на русский они говорят, что моделируют некую динамическую систему дифференциальными уравнениями (о ужас), и выбирают непосредственно управление, минимизируя какую-то квадратичную функцию (о! я чувствую приближение наименьших квадратов). Так, хорошо. Пытаемся читать дальше:
Finite-horizon, continuous-time LQR,
[серия ужасных формул]
Пропускаем, ну его в болото такое читать, кроме того, явно будет противно руками считать непрерывные функции.
Infinite-horizon, continuous-time LQR,
[серия ещё более ужасных формул]
Час от часу не легче, ещё и несобственные интегралы пошли, пропускаем, вдруг дальше что интересного найдём.
Finite-horizon, discrete-time LQR
О, это я люблю. У нас дискретная система, смотрим её состояние через некие промежутки (некие промежутки в первом прочтении всегда равны одной секунде) времени. Производные из уравнения ушли, т.к. они теперь могут быть приближены как (x_{k+1}-x_{l})/1 секунду. Теперь неплохо было бы понять, что такое x_k.
Одномерный пример
Фейнман писал, как именно он читал все уравнения, что ему приходилось:
Actually, there was a certain amount of genuine quality to my guesses. I had a scheme, which I still use today when somebody is explaining
something that I'm trying to understand: I keep making up examples. For instance, the mathematicians would come in with a terrific theorem, and they're all excited. As they're telling me the conditions of the theorem, I construct something which fits all the conditions. You know, you have a set (one ball) — disjoint (two balls). Then the balls turn colors, grow hairs, or whatever, in my head as they put more conditions on. Finally they state the theorem, which is some dumb thing about the ball which isn't true for my hairy green ball thing, so I say, «False!»
Ну а мы что, круче Фейнмана? Лично я нет. Поэтому давайте так. Имеется автомобиль, едущий с некой начальной скоростью. Задача его разогнать до некой финальной скорости, при этом единственное, на что мы можем влиять, это на педаль газа, сиречь на ускорение автомобиля.
Давайте представим, автомобиль идеален и движется по такому закону:

x_k — это скорость автомобиля в секунду k, u_k — это положение педали газа, которое мы захотим, можно её интерпретировать как ускорение в секунду k. Итого, мы стартуем с некой скорости x_0, и затем проводим вот такое численное интегрирование (во какие слова пошли). Отметьте, что я не складываю м/с и м/с^2, u_k умножается на одну секунду интервала между измерениями. По умолчанию у меня все коэффициенты либо ноль, либо один.
Итак, чтобы понять, что происходит, я пишу вот такой код (я пишу очень много одноразового кода, который выкидываю сразу после написания). Привожу листинг здесь на всякий случай, как обычно, я использую OpenNL для решения больших разреженных линейных систем уравнений.
Скрытый текст
#include <iostream>
#include "OpenNL_psm.h"
int main() {
const int N = 60;
const double xN = 2.3;
const double x0 = .5;
const double hard_penalty = 100.;
nlNewContext();
nlSolverParameteri(NL_NB_VARIABLES, N*2);
nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE);
nlBegin(NL_SYSTEM);
nlBegin(NL_MATRIX);
nlBegin(NL_ROW); // x0 = x0
nlCoefficient(0, 1);
nlRightHandSide(x0);
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
nlBegin(NL_ROW); // xN = xN
nlCoefficient((N-1)*2, 1);
nlRightHandSide(xN);
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
nlBegin(NL_ROW); // uN = 0, for convenience, normally uN is not defined
nlCoefficient((N-1)*2+1, 1);
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
for (int i=0; i<N-1; i++) {
nlBegin(NL_ROW); // x{i+1} = xi + ui
nlCoefficient((i+1)*2 , -1);
nlCoefficient((i )*2 , 1);
nlCoefficient((i )*2+1, 1);
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
}
for (int i=0; i<N; i++) {
nlBegin(NL_ROW); // xi = xN, soft
nlCoefficient(i*2, 1);
nlRightHandSide(xN);
nlEnd(NL_ROW);
}
nlEnd(NL_MATRIX);
nlEnd(NL_SYSTEM);
nlSolve();
for (int i=0; i<N; i++) {
std::cout << nlGetVariable(i*2) << " " << nlGetVariable(i*2+1) << std::endl;
}
nlDeleteContext(nlGetCurrent());
return 0;
}
Итак, давайте разбираться, что я делаю. Для начала я говорю N=60, на всё отвожу 60 секунд. Затем говорю, что финальная скорость должна быть 2.3 метра в секунду, а начальная полметра в секунду, это выставлено от балды. Переменных у меня будет 60*2 — 60 значений скорости и 60 значений ускорения (строго говоря, ускорения должно быть 59, но мне проще сказать, что их 60, а последнее должно быть равно строго нулю).
Итого, у меня 2*N переменных (N=60), чётные переменные (я начинаю считать с нуля, как и всякий нормальный программист) — это скорость, а нечётные — это ускорение. Задаю начальную и конечную скорость вот этими строчками:
По факту, я сказал, что хочу, чтобы начальная скорость была равна x0 (.5m/s), а конечная — xN (2.3m/s).
nlBegin(NL_ROW); // x0 = x0
nlCoefficient(0, 1);
nlRightHandSide(x0);
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
nlBegin(NL_ROW); // xN = xN
nlCoefficient((N-1)*2, 1);
nlRightHandSide(xN);
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
Мы знаем, что x{i+1} = xi + ui, поэтому давайте добавим N-1 такое уравнение в нашу систему:
for (int i=0; i<N-1; i++) {
nlBegin(NL_ROW); // x{i+1} = xi + ui
nlCoefficient((i+1)*2 , -1);
nlCoefficient((i )*2 , 1);
nlCoefficient((i )*2+1, 1);
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
}
Итак, мы добавили всё жёсткие ограничения в систему, а что именно, собственно, мы можем хотеть оптимизировать? Давайте просто для начала скажем, что мы хотим, чтобы x_i как можно скорее достиг финальной скорости xN:
for (int i=0; i<N; i++) {
nlBegin(NL_ROW); // xi = xN, soft
nlCoefficient(i*2, 1);
nlRightHandSide(xN);
nlEnd(NL_ROW);
}
Ну вот наша система готова, жёсткие правила перехода между состояниями заданы, квадратичная функция качества системы тоже, давайте потрясём коробочку и посмотрим, что наименьшие квадраты нам дадут в качестве решения x_i, u_i (красная линия — это скорость, зелёная — ускорение):
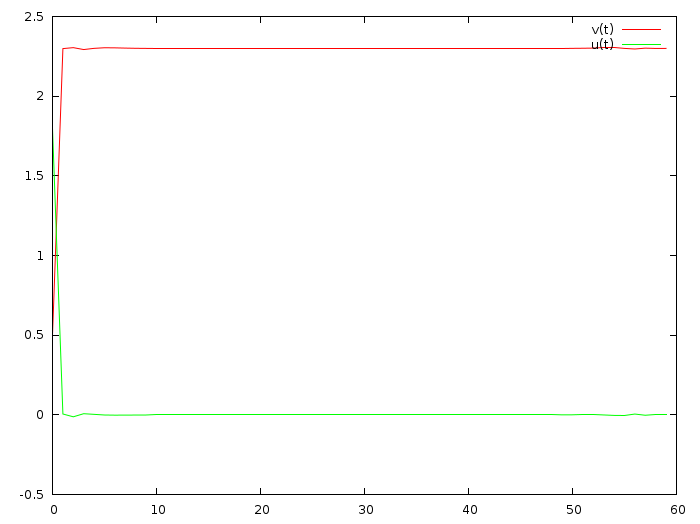
Ооокей, мы действительно ускорились с полуметра в секунду до двух метров запятая трёх в секунду, но уж больно большое ускорение наша система выдала (что логично, т.к. мы потребовали сойтись как можно скорее).
А давайте изменим (вот коммит) целевую функцию, вместо наискорейшей сходимости попросим как можно меньшее ускорение:
for (int i=0; i<N; i++) {
nlBegin(NL_ROW); // ui = 0, soft
nlCoefficient(i*2+1, 1);
nlEnd(NL_ROW);
}
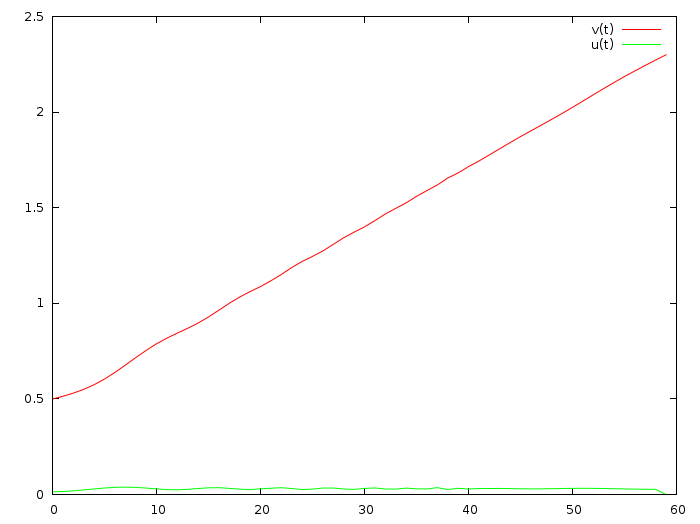
Мда, теперь машина ускоряется на два метра в секунду за целую минуту. Ок, давайте и быструю сходимость к финальной скорости, и маленькое ускорение попробуем (вот коммит)?
for (int i=0; i<N; i++) {
nlBegin(NL_ROW); // ui = 0, soft
nlCoefficient(i*2+1, 1);
nlEnd(NL_ROW);
nlBegin(NL_ROW); // xi = xN, soft
nlCoefficient(i*2, 1);
nlRightHandSide(xN);
nlEnd(NL_ROW);
}
Ага, супер, теперь становится красиво:
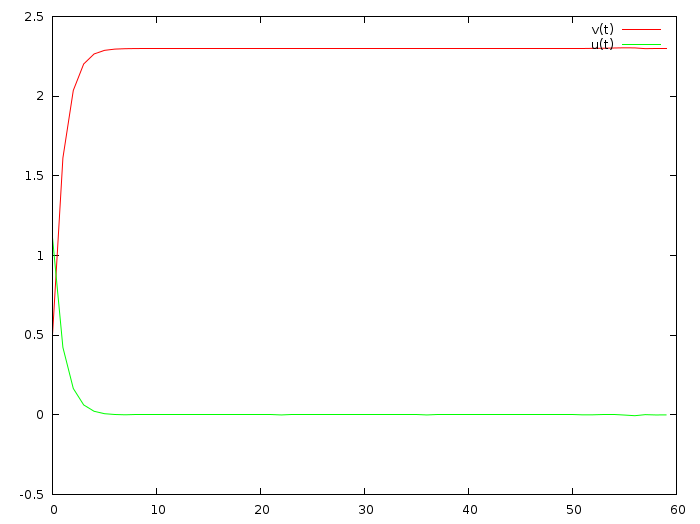
Итак, быстрая сходимость и ограничение величины управления — это конкурирующие цели, понятно. Обратите внимание, на данный момент я остановился на первой строчке параграфа википедии, дальше идут страшные формулы, я их не понимаю. Зачастую чтение статей сводится к поиску ключевых слов и полному выводу всех результатов, используя тот матаппарат, которым лично я владею.
Итак, что мы имеем на данный момент? То, что имея начальное состояние системы + имея конечное состояние системы + количество секунд, мы можем найти идеальное управление u_i. Это хорошо, только к сигвею слабо применимо. Чёрт, как же они делают-то? Так, читаем следующий текст в википедии:
with a performance index defined as
the optimal control sequence minimizing the performance index is given by
where [ААА, ЧТО ТАМ ДАЛЬШЕ ТАКОЕ?!]
Так. Я не понимаю что после знака равно в формуле «J = ...», но это явно квадратичная функция, что мы попробовали. Типа, скорейшей сходимости к цели плюс наименьшими затратами, это мы позже посмотрим ближе, сейчас мне достаточно моего понимания.
u_k = -F x_k. Оп-па. Они говорят, что для нашего одномерного примера в любой момент времени оптимальное ускорение — это некая константа -F, помноженная на текущую скорость? Ну-ка, ну-ка. А ведь и правда, зелёный и красный графики подозрительно друг на друга похожи!
Давайте-ка попробуем написать настоящие уравнения для нашего 1D примера.
Итак, у нас есть функция качества управления:
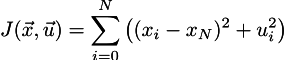
Мы хотим её минимизировать, при этом соблюдая ограничения на связь между соседними значениями скорости нашей машины:
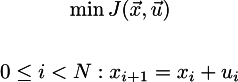
Стоп-стоп-стоп, а какого хрена в википедии стоит x_k^T Q x_k? Ведь это же простой x_k^2 в нашем случае, а у нас (x_k-x_N)^2?! Ёлки, да ведь они предполагают, что финальное состояние, в которое мы хотим попасть, это нулевой вектор!!! КАКОГО [CENSORED] ОБ ЭТОМ НА ВСЕЙ СТРАНИЦЕ ВИКИПЕДИИ НИ СЛОВА?!
Окей, дышим глубоко, успокаиваемся. Теперь я все x_i в формулировке J выражу через u_i, чтобы не иметь ограничений. Теперь у меня переменными будет являться только вектор управления. Итак, мы хотим минимизировать функцию J, которая записывается вот так:
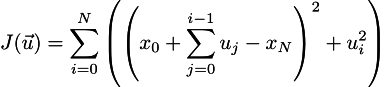
Зашибись. А теперь давайте раскрывать скобки (см. эпиграф):
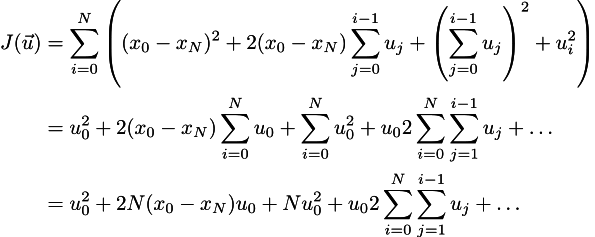
Многоточие здесь означает всякую муть, которая от u_0 не зависит. Так как мы ищем минимум, то чтобы его найти, нужно приравнять нулю все частные производные, но для начала меня интересует частная производная по u_0:
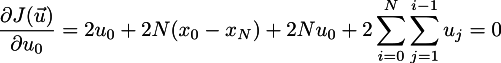
Итого мы получаем, что оптимальное управление будет оптимально только тогда, когда u_0 имеет вот такое выражение:
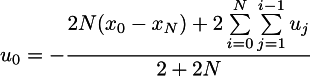
Обратите внимание, что в это выражение входят и другие неизвестные u_i, но есть одно «но». Прикол в том, что я не хочу, чтобы машина ускорялась всю минуту на всего два метра в секунду. Минуту я ей дал просто как заведомо достаточное время. А могу и час дать. Член, зависящий от u_i, если грубо, то это вся работа по ускорению, от N она не зависит. Поэтому если N достаточно большой, то оптимальный u_0 линейно зависит только от того, насколько x0 далёк от конечного положения!
То есть, управление должно выглядеть следующим образом: мы моделируем систему, находим магический коэффициент, линейно связывающий u_i и x_i, записываем его, а затем в нашем роботе просто делаем линейный пропорциональный регулятор, используя найденный магический коэффициент!
Если быть предельно честным, то до вот этого момента я кода, конечно, не писал, всё вышеозначенное я проделал в уме и чуть-чуть на бумажке. Но это не отменяет факта, что одноразового кода я пишу действительно много.
2D пример
В качестве интуиции это прекрасно, а вот первый код, который я действительно написал:
Скрытый текст
#include <iostream>
#include <vector>
#include "OpenNL_psm.h"
int main() {
const int N = 60;
const double x0 = 3.1;
const double v0 = .5;
const double hard_penalty = 100.;
const double rho = 16.;
nlNewContext();
nlSolverParameteri(NL_NB_VARIABLES, N*3);
nlSolverParameteri(NL_LEAST_SQUARES, NL_TRUE);
nlBegin(NL_SYSTEM);
nlBegin(NL_MATRIX);
nlBegin(NL_ROW);
nlCoefficient(0, 1); // x0 = 3.1
nlRightHandSide(x0);
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
nlBegin(NL_ROW);
nlCoefficient(1, 1); // v0 = .5
nlRightHandSide(v0);
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
nlBegin(NL_ROW);
nlCoefficient((N-1)*3, 1); // xN = 0
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
nlBegin(NL_ROW);
nlCoefficient((N-1)*3+1, 1); // vN = 0
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
nlBegin(NL_ROW); // uN = 0, for convenience, normally uN is not defined
nlCoefficient((N-1)*3+2, 1);
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
for (int i=0; i<N-1; i++) {
nlBegin(NL_ROW); // x{N+1} = xN + vN
nlCoefficient((i+1)*3 , -1);
nlCoefficient((i )*3 , 1);
nlCoefficient((i )*3+1, 1);
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
nlBegin(NL_ROW); // v{N+1} = vN + uN
nlCoefficient((i+1)*3+1, -1);
nlCoefficient((i )*3+1, 1);
nlCoefficient((i )*3+2, 1);
nlScaleRow(hard_penalty);
nlEnd(NL_ROW);
}
for (int i=0; i<N; i++) {
nlBegin(NL_ROW); // xi = 0, soft
nlCoefficient(i*3, 1);
nlEnd(NL_ROW);
nlBegin(NL_ROW); // vi = 0, soft
nlCoefficient(i*3+1, 1);
nlEnd(NL_ROW);
nlBegin(NL_ROW); // ui = 0, soft
nlCoefficient(i*3+2, 1);
nlScaleRow(rho);
nlEnd(NL_ROW);
}
nlEnd(NL_MATRIX);
nlEnd(NL_SYSTEM);
nlSolve();
std::vector<double> solution;
for (int i=0; i<3*N; i++) {
solution.push_back(nlGetVariable(i));
}
nlDeleteContext(nlGetCurrent());
for (int i=0; i<N; i++) {
for (int j=0; j<3; j++) {
std::cout << solution[i*3+j] << " ";
}
std::cout << std::endl;
}
return 0;
}
Здесь всё то же самое, только переменных системы теперь две: не только скорость, но и координата машины.
Итак, дана начальная позиция + начальная скорость (x0, v0), мне нужно достичь конечной позиции (0,0), остановиться в начале координат.
Переход из одного момента в следующий осуществляется как x_{k+1} = x_k + v_k, а v_{k+1} = v_k + u_k.
Я достаточно прокомментировал предыдущий код, этот не должен вызвать трудностей. Вот результат работы:
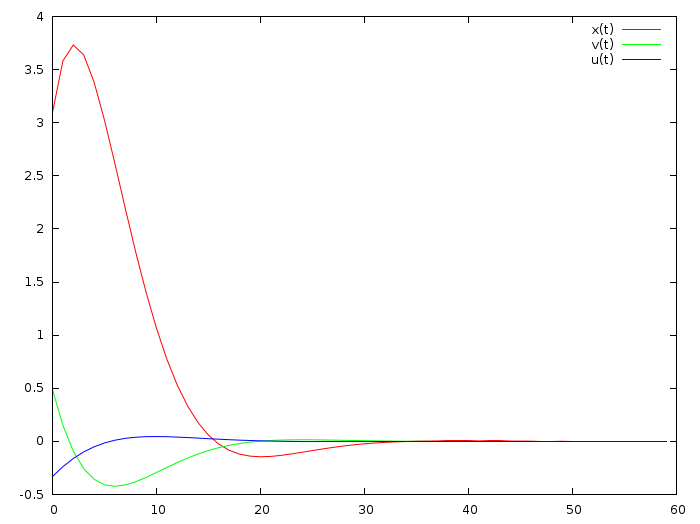
Красная линия — координата, зелёная — скорость, а синяя — это непосредственно положение «педали газа». Исходя из предыдущего, предполагается, что синяя кривая — это взвешенная сумма красной и зелёной. Хм, так ли это? Давайте попробуем посчитать!
То есть, теоретически, нам нужно найти два числа a и b, такие, что u_i = a*x_i + b*v_i. А это есть не что иное, как линейная регрессия, что мы делали в прошлой статье! Вот код.
В нём я сначала считаю кривые, что на картинке выше, а затем ищу такие a и b, что синяя кривая = a*красная + b*зелёная.
Вот разница между настоящими u_i и теми, что я получил, складывая зелёную и красную прямую:
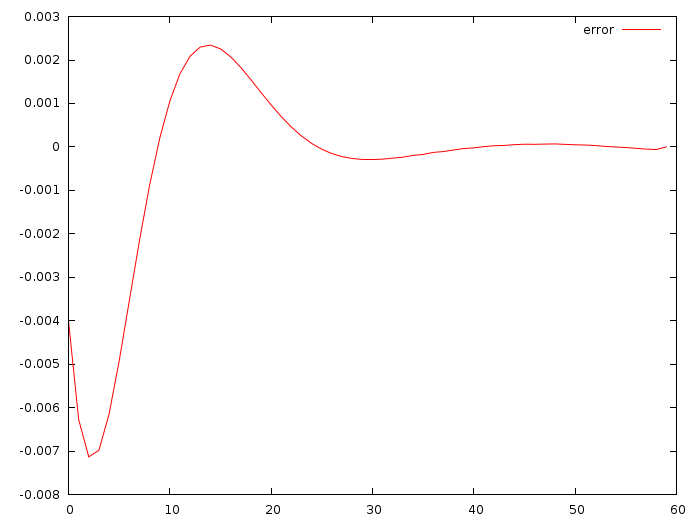
Отклонение порядка одной сотой метра за секунду за секунду! Круто!!! Тот коммит, что я привёл, даёт a=-0.0513868, b=-0.347324. Отклонение действительно небольшое, но ведь это нормально, начальные данные-то я не менял.
А теперь давайте кардинально изменим начальное положение и скорость машины, оставив магические числа a и b из предыдущих вычислений.
Вот разница между настоящим оптимальным решением и тем, что мы получаем наитупейшей процедурой, давайте-ка я её ещё раз приведу полностью:
double xi = x0;
double vi = v0;
for (int i=0; i<N; i++) {
double ui = xi*a + vi*b;
xi = xi + vi;
vi = vi + ui;
std::cout << (ui-solution[i*3+2]) << std::endl;
}
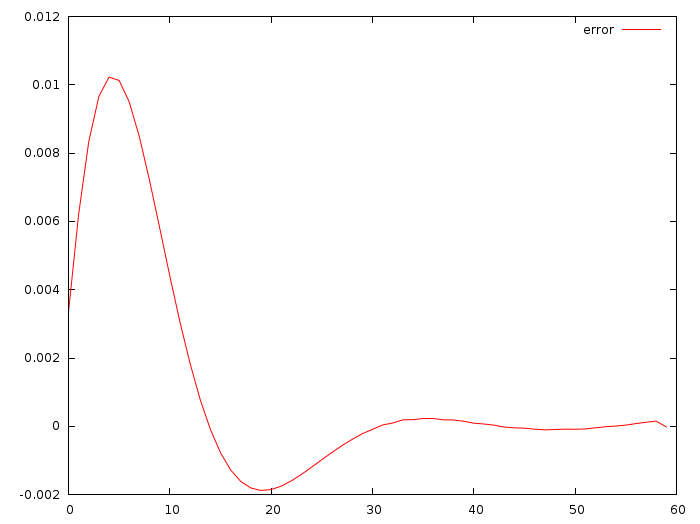
И никаких дифференциальных уравнений Риккати, которые нам предлагала википедия. Возможно, что и про них мне придётся почитать, но это будет потом, когда припечёт. А пока что простые квадратичные функции меня устраивают более чем полностью.
Сухой остаток
Итого: чтобы это использовать, будут две основных трудности:
а) найти хорошие матрицы перехода A и B, это нужно будет записывать кинематические уравнения, так как, конечно, там всё будет зависеть от масс объектов и прочего
б) найти хорошие коэффициенты компромисса между целями наискорейшего схождения к цели, но при этом ещё и не делая сверхусилий.
Если а и б сделать, то метод выглядит многообещающим. Единственное, что он требует полного знания состояния системы, что не всегда получается. Например, положение сигвея мы не знаем, можем только догадываться о нём, исходя из данных датчиков типа гироскопа и акселерометра. Ну да это про это я расскажу своим студентам в следующий раз.
Итак, я хотел добиться трёх целей:
а) понять, что такое lqr
б) объяснить то, что понял, студентам и вам
в) показать вам и моим студентам, что я (как и большинство людей) ни хрена не понимаю в математических текстах, что печально, но совсем не катастрофично. Ищем ключевые слова, за которые зацепиться, выкидываем излишние, ненужные нам методы и абстракции, и пытаемся это впихнуть в рамки наших текущих знаний.
Надеюсь, мне удалось. Ещё раз, я совсем не специалист в теории управления, я её в глаза не видел, если у вас есть что дополнить и поправить, не стесняйтесь.
Enjoy!