
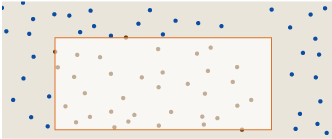
На этом снимке запечатлена сетчатая столешница стола в патио, сфотографированная после сильного дождя. В некоторых отверстиях сетки задержались капли воды. Что можно сказать о распределении этих капель? Разбросаны ли они случайно по поверхности? Процесс падения дождя, расположивший их, кажется достаточно случайным, но на мой взгляд, паттерн занятых в сетке мест выглядит подозрительно ровным и однообразным.
Чтобы упростить анализ, я выделил квадратную часть фотографии со столешницей (убрав отверстие для зонта), и выделил координаты всех капель в этом квадрате. Всего в нём 394 капель, которые я обозначил синими точками:

Повторю вопрос: выглядит ли этот паттерн как результат случайного процесса?
Я пришёл к этому вопросу после написания статьи для American Scientist, в которой изучаются два варианта симулируемой случайности: псевдо и квази. Псевдослучайность в представлении не нуждается. Псевдослучайный алгоритм выбора точек в квадрате стремится гарантировать, что все точки имеют одинаковую вероятность выбора, и что все выборы независимы друг от друга. Вот массив из 394 псевдослучайных точек, ограниченных принадлежностью скошенной и повёрнутой сетке, похожей на сетчатую столешницу:

Квазислучайность — это менее известная концепция. При выборе квазислучайных точек целью является не равновероятность или независимость, а равномерность распределения: как можно более равномерный разброс точек по поверхности квадрата. Однако не слишком очевидно, как достичь этой цели. Для 394 показанных ниже квазислучайных точек координаты x образуют простую арифметическую прогрессию, но координаты y изменены процессом перемешивания цифр. (Соответствующий алгоритм изобретён в 1930-х голландским математиком Йоханнесом ван дер Корпутом, работавшим над одномерными рядами, и в 1950-х был перенесён в два измерения Клаусом Фридрихом Ротом. Подробнее см. в моей статье для American Scientist на странице 286 или в потрясающей книге Иржи Матусека.)

Какое из этих множеств точек, псевдо или квази, лучше соответствует каплям дождя? Мы можем сравнить все три паттерна в уменьшенном виде:

Каждый из паттернов имеет собственную текстуру. В псевдослучайном есть и сконцентрированные кластеры, и большие пробелы. Квазислучайные точки расположены более равномерно (хотя и есть несколько близких пар точек), но они тоже создают отчётливые маломасштабные повторяющиеся узоры, наиболее заметной из которых является шестиугольная структура, повторяемая почти с кристаллической равномерностью. Что касается капель, то похоже, они распределены по площади почти с равномерной плотностью (в этом напоминая квазислучайный паттерн), но в текстуре присутствуют скорее намёки на изгибы, а не на решётчатые структуры (в этом она больше походит на псевдослучайный пример).
Вместо того, чтобы изучать паттерны «на глазок», можно попробовать количественный подход к их описанию и классификации. Для этой цели существует множество инструментов: функции радиального распределения, статистика ближайших соседей, методы Фурье, но основной причиной решения этого вопроса для меня стала в первую очередь возможность поиграть с новой игрушкой, которую я изучил в процессе изучения квазислучайности. Это качество, называемое расхождением (discrepancy) (прим. пер.: не удалось найти правильного термина на русском, так что напишите мне, если знаете его), оценивает отклонение множества точек от равномерного распределения в пространстве.
В концепции расхождения есть множество вариаций, но я хочу рассмотреть только одну схему измерения. Идея заключается в наложении на паттерн прямоугольников различной формы и размеров, стороны которых параллельны осям x и y. Вот три примера прямоугольников, наложенных на паттерн капель:

Теперь посчитаем количество точек, заключённых в каждый прямоугольник, и сравним их с числом точек, которые должны быть заключены в него при соответствующей площади, если бы распределение точек было идеально равномерным по всему квадрату. Абсолютное значение разности является расхождением
где
Для паттерна в целом мы можем задать общее расхождение D как наихудшее значение его изменения, или, другими словами, максимальное расхождение, взятое для всех возможных прямоугольников, наложенных на квадрат. Ван дер Корпут задавался вопросом, могут ли множества точек быть созданы с произвольно низким расхождением, так что при
Как найти прямоугольник с максимальным расхождением для заданного множества точек? Когда я впервые прочитал определение расхождения, я подумал, что вычислить его точно будет невозможно, потому что существует бесконечное множество рассматриваемых прямоугольников. Но поразмышляв, я осознал, что существует только конечное множество прямоугольников-кандидатов, имеющих возможность максимизировать расхождение. Это прямоугольники, в которых каждая из четырёх сторон проходит хотя бы через одну точку. (Исключение: прямоугольники-кандидаты также могут иметь стороны, лежащие на границах квадрата.)
Допустим, мы встретили следующий прямоугольник:
Левая, верхняя и нижняя стороны проходят через точку,, но правая сторона лежит в «пустом пространстве». Такая конфигурация не может быть прямоугольником с максимальным расхождением. Мы можем сдвигать правое ребро влево, пока оно не пересечётся с точкой:

Это изменение формы уменьшает площадь прямоугольника, не изменяя количество заключённых в него точек, а потому увеличивает плотность точек. Мы также можем сдвинуть ребро в другую сторону:

Теперь мы увеличили площадь, снова не изменив количество заключённых в неё точек, а значит, снизили плотность. Как минимум одно из этих действий увеличит
Существует ещё и другой надоедливый вопрос: должен ли прямоугольник считаться «замкнутым» (то есть точки на границе включаются в площадь) или «открытым» (точки на границах исключаются). Я уклонился от этой задачи, представив в виде таблицы результаты и для замкнутых, и для открытых границ. Замкнутая форма даёт наибольшее расхождение для прямоугольников с плотным расположением точек, а открытая форма максимизирует расхождение при низкой плотности точек.
Рассматривая только экстремумы функции расхождения, мы делаем задачу подсчёта конечной — но всё не так просто! Сколько прямоугольников нужно рассматривать в квадрате с
Один из способов снизить вычислительные затраты — вернуться к более простому измерению расхождения. В разной литературе по квазислучайным паттернам в двух и более измерениях используется качество, называемое «расхождением-звезда» (star discrepancy), или D*. Идея заключается в том, чтобы рассматривать только прямоугольники, «прикреплённые» к левому нижнему углу квадрата (который удачно совпадает с точкой начала координат плоскости xy). В этом случае количество прямоугольников равно всего
Вот прямоугольник, определяющий глобальное расхождение-звезда паттерна дождевых капель:

Тёмно-зелёный прямоугольник внизу закрывает примерно 55 процентов квадрата и должен содержать при совершенно равномерном распределении 216,9 точек. На самом деле в него входит (считая, что это «замкнутый» прямоугольник) 238 точек, то есть расхождение равно 21,1. Ни один другой прямоугольник, привязанный к углу (0,0), не будет иметь большего расхождения. (Примечание: из-за ограничений графического разрешения кажется, что прямоугольник D* растянут до границ квадрата, на самом деле правое ребро лежит на x = 0,999395.)
Что говорит нам этот результат о природе паттерна капель дождя? Ну, для начала, расхождение довольно близко к
А как насчёт вычисления неограниченного расхождения D, то есть изучения всех прямоугольников, а не только закреплённых прямоугольников D*? Поразмыслив, можно прийти к выводу, что всеобъемлющее перечисление прямоугольников не сможет в этом случае изменить основной вывод; D никогда не может быть меньше D*, и поэтому мы не можем надеяться приблизиться от
Очевидный и простой алгоритм для D генерирует по очереди все прямоугольники-кандидаты, измеряет их площадь, считает точки внутри и отслеживает предельные расхождения, обнаруженные в процессе. Я выяснил, что программа, реализующая этот алгоритм, может определить точное расхождение 100 псевдослучайных или квазислучайных точек за несколько минут. Этот результат может мотивировать нас взять большие значения N; однако время выполнения почти удваивается каждый раз, когда N увеличивается на 10, и это намекает нам, что для N = 394 вычисления займут пару веков.
Я потратил несколько дней на попытки ускорить вычисления. БОльшая часть времени выполнения тратится на процедуру, считающую точки в каждом прямоугольнике. Определение того, находится ли заданная точка внутри, снаружи или на границе, занимает восемь арифметических сравнений; то есть при N = 394 выполняется более 3 000 для каждого из шести миллиардов прямоугольников. Наиболее эффективным обнаруженным мной способом экономии времени стало предварительное вычисление всех сравнений. Для каждой точки, которая может стать нижним левым углом прямоугольника я предварительно вычисляю список всех точек паттерна, находящихся выше и правее. Для каждого потенциального правого верхнего угла прямоугольника я собираю похожий список точек ниже и левее. Эти списки хранятся в хеш-таблице, индексированной по координатам угла. Для каждого треугольника я могу вычислить количество внутренних точек, просто взяв пересечение множеств двух списков.
Благодаря этому трюку ожидаемое время выполнения при N = 394 снижается с двух веков до примерно двух недель. Эта отличная оптимизация стимулировала меня потратить ещё один день на дальнейшие улучшения. Немного улучшила ситуацию замена хеш-таблицы на массив N × N. А затем я нашёл способ игнорировать все наименьшие треугольники, которые не могут вероятными прямоугольниками с максимальным D, потому что в них содержится слишком мало точек, или они имеют слишком малую площадь. Это улучшение наконец позволило снизить время выполнения до одной ночи. Для вычисления иллюстрации, показывающей прямоугольник с максимальным расхождением D для паттерна дождевых капель, потребовалось шесть часов.

Прямоугольник с max-D очевидно стал небольшим уточнением прямоугольника D* для того же множества точек. Прямоугольник D «должен» содержать 204,3 точек, но на самом деле содержит 229, что даёт нам расхождение D = 24,7. Разумеется, знание того, что точное расхождение равно 24,7, а не 21,1, ничего не говорит нам о природе самого паттерна дождевых капель. На самом деле, мне кажется, что проводя всё больше и больше вычислений, я узнаю о нём всё меньше и меньше.
Когда я начинал работу над этим проектом, у меня была собственная теория о том, что может происходить в столешнице для сглаживания распределения капель и что делает паттерн больше квази-, чем псевдослучайным. Для начала я подумал о каплях, лежащих на гладкой поверхности стекла, а не металлической сетке. Если две небольшие капли достаточно сблизятся, чтобы коснуться, они сольются в одну большую каплю, потому что эта конфигурация имеет меньшую энергию, связанную с поверхностным натяжением. Если две соседние ячейки сетки заполнены водой, и если металл между ними мокрый, то вода может свободно перетекать от одной капли к другой. Капля большего размера почти наверняка вырастет за счёт меньшей, а последняя со временем исчезнет. Следовательно, по сравнению с чисто случайным распределением мы можем ожидать нехватку капель в соседних ячейках.
И эта мысль по-прежнему кажется мне очень хорошей. Единственная проблема заключается в том, что она объясняет явление, которого может и не существовать. Я не знаю, раскрыли ли мои вычисления расхождения что-то важное про эти три паттерна, но, по крайней мере, измерениями не удалось доказать, что распределение капель отличается от псевдослучайного. На самом деле, паттерны выглядят разными, но насколько мы можем доверять своим органам восприятия в таких случаях? Если попросить людей нарисовать точки случайным образом, большинство справится с этим плохо, обычно распределение будет оказываться слишком плавным и ровным. Возможно, мозг испытывает подобные же трудности при распознавании случайности.
Тем не менее, я полагаю, что существует какое-нибудь математическое свойство, позволяющее более эффективно разделить эти паттерны. Если кто-нибудь ещё решит потратить своё время на поиски, то координаты xy для трёх множеств точек лежат в текстовом файле.
Дополнение: это просто краткая рекомендация — если вы дочитали досюда, то продолжите чтение комментариев. В них есть много ценного. Я хочу поблагодарить всех тех, кто потратил своё время, чтобы предложить альтернативные объяснения или алгоритмы и чтобы указать на слабые места в моём анализе. Особое спасибо themathsgeek, который через 40 минут после опубликования поста написал гораздо более качественную программу для вычисления расхождений. Также я благодарю Iain, который проверил мои импровизированные рассуждения о восприятии случайных паттернов настоящими экспериментами.