Comments 8
Какое отношение к этому имеет Эйлер и при каких обстоятельствах это произошло?
На хабре уже было https://habr.com/ru/post/454136/ и куда проработанней
Вот почему π называют иррациональным числом — его нельзя записать в виде конечного числа цифр после запятой.
Число π называют иррациональным не поэтому. Есть масса рациональных чисел, которые нельзя записать в виде десятичной дроби с конечным числом цифр после запятой.
Да, логика в статье поломанная, если она вообще есть:
В общем, вместо чтения этой статьи лучше почитать классику жанра (первые пару глав по числам):
Курант Р., Роббинс Г. Что такое математика?
- у любого рационального числа после запятой периодическая дробь, например 1/3 = 0.(3), и это работает в обратную сторону;
- у иррациональных чисел никакого периода после запятой не наблюдается.
В общем, вместо чтения этой статьи лучше почитать классику жанра (первые пару глав по числам):
Курант Р., Роббинс Г. Что такое математика?
Основное значение слова «иррациональный» в русском языке — это «не поддающийся разумному объяснению», а вовсе не «дробный». И это запутывает абсолютное большинство начинающих изучать математику, нагружая понятие иррационального числа какой-то дополнительной магией. Если же вспомнить значения исходно латинского ratio, из которого в русский перешло только «рацио», но не «отношение» — то все встанет на свои места. Нет никаких «необъяснимых» чисел, есть просто числа, которые невозможно представить отношением, т.е. дробью. При любых натуральных числителе и знаменателе. Если бы еще в школе рациональные и иррациональные числа заменили бы на «дробно-представимые» и «дробно-непредставимые» — понятия было бы намного больше
А мне более осмысленной кажется формула
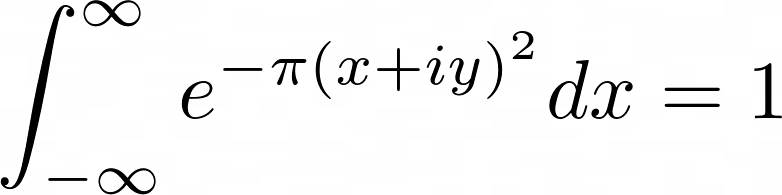
Семь особенных чисел вместо пяти. И пара бесконечностей до кучи.
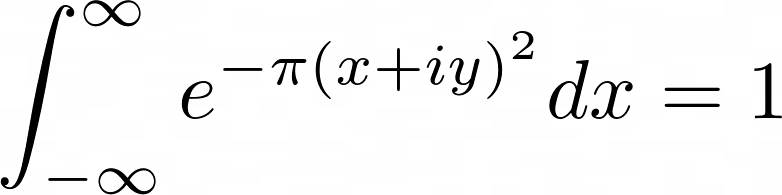
Семь особенных чисел вместо пяти. И пара бесконечностей до кучи.
Sign up to leave a comment.
Тождество Эйлера — самое красивое математическое уравнение